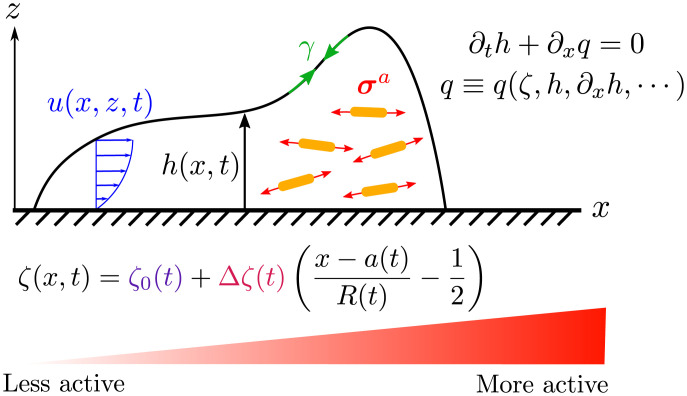
Fig. 2.

Model of an active drop moving on a substrate. The horizontal flow velocity $u(x,z,t)$ driven by active internal stresses (${\mathit{\sigma }}^a$) and surface tension (γ) adopts a Poiseuille-like profile in the drop interior, characteristic of lubrication theory. The drop height h(x, t) obeys the continuity equation (Eq. 1) with a flux q that encodes the constitutive relation (Eq. 3) for how activity drives fluid flow. The spatial profile of activity ($\zeta (x,t)$) is a simple linear ramp with a constant offset, allowing for both drop translation and size change (Eq. 7).