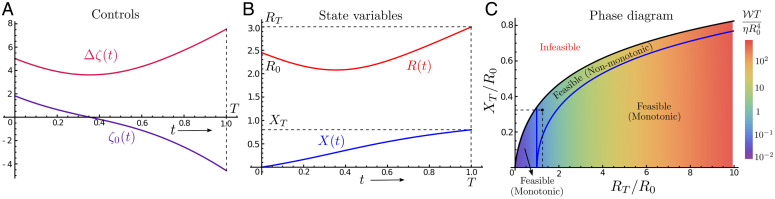
Fig. 3.

ODE optimal control. (A and B) Sample trajectories for the globally optimal mean (ζ₀) and gradient ($\mathrm{\Delta }\zeta$) activity are shown in A, and the associated controlled dynamics for the drop position (X) and size (R) are shown in B. The parameters chosen are $X_T=0.8,\hspace{0.17em}{R}_0=\sqrt{6}$, R_T = 3, T = 1, and $\eta =0.1$. Note that as η sets a time scale, only the ratio $T/\eta$ is important. For these parameter values, we see that the size change is nonmonotonic, which is reflected in the sign change in the mean activity ${\zeta }_0(t)$. The initial contractile activity (${\zeta }_0>0$) causes the drop to shrink and consequently accelerate its translation, and, later, the activity switches over to become extensile (${\zeta }_0<0$) to allow the drop to reach its larger final size R_T. (C) The phase diagram here represents the feasibility region for optimal transport of a parabolic active drop, as a function of the nondimensionalized drop displacement ($X_T/R_0$) and its size disparity ($R_T/R_0$). The black curve is the maximum achievable displacement X_T for a given relative change in size ($R_T/R_0$), beyond which no smooth optimal controls exist. Below the black curve is the feasible region, with the shaded color representing the total work done [nondimensionalized as $\mathcal{W}T/(\eta R_0^4)$] by the globally optimal policy, with the cost increasing from blue to red. The blue curves in the shaded region demarcate the parameter space where the global optimizer has a monotonic or nonmonotonic size dependence as a function of time. Nonmonotonic changes in size are favored in the region bordered by the blue and black curves and only occur when $R_T>R_0$. For $R_T<R_0$, the optimal policies have a monotonic size dependence. The black dot corresponds to the solution shown in A and B.