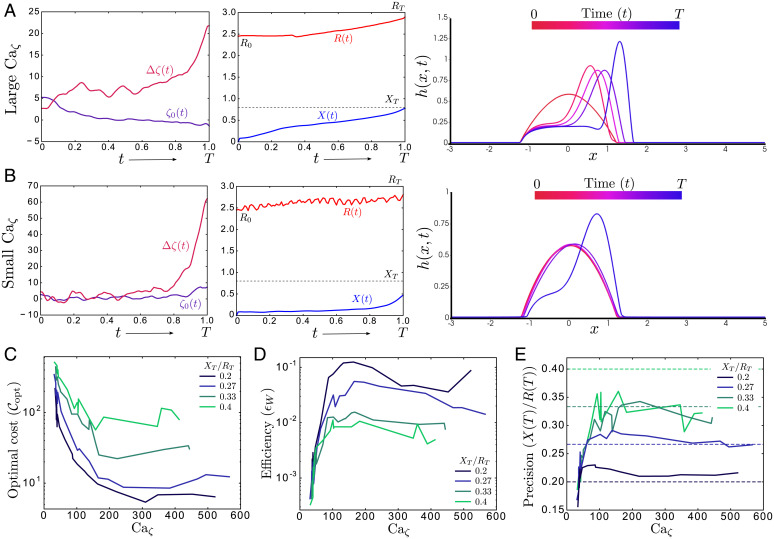
Fig. 4.

PDE optimal control. (A) The optimal activity controls (${\zeta }_0(t),\hspace{0.17em}\mathrm{\Delta }\zeta (t)$; Left) and corresponding trajectories for the state variables ($X(t),\hspace{0.17em}R(t)$; Center) and the full drop profile (h(x, t); Right), obtained by numerical optimization for small surface tension or large active capillary number ($\gamma =0.15$, Ca${}_{\zeta }=383.66$). The drop adopts a strongly asymmetric shape, with an advancing peak and receding tail, like in ref. 25. (B) Similar plots with the optimal activity controls (${\zeta }_0(t),\hspace{0.17em}\mathrm{\Delta }\zeta (t)$; Left), and corresponding drop trajectory ($X(t),\hspace{0.17em}R(t)$, Center; h(x, t), Right), now obtained for large surface tension or small active capillary number (γ = 2, Ca${}_{\zeta }=30.91$). The transport plan fares poorly as the drops fails to reach the desired final position and size and wastes a significant amount of energy in futile size oscillations (R(t); Center) that don’t aid in transport. Both A and B are computed by using $X_T=0.8$ and R_T = 3 ($X_0=0$ and $R_0=\sqrt{6}$ is kept fixed throughout), though similar policies are obtained for other values of $X_T/R_T$ as well. (C–E) The total cost (${\mathcal{C}}_{\text{opt}}$; C), efficiency (ϵ_W [Eqs. 13 and 14]; D), and precision ($X(T)/R(T)$; E) of the numerically computed optimal transport protocol plotted against Ca${}_{\zeta }$, for different tasks labeled by increasing $X_T/R_T$ (blue to green). Remarkably, the performance curves present an optimal trade-off in balancing active forces against passive ones to attain improved drop transport plans at intermediate values of Ca${}_{\zeta }$.