RNAloops: a database of RNA multiloops

Abstract

Motivation

Knowledge of the 3D structure of RNA supports discovering its functions and is crucial for designing drugs and modern therapeutic solutions. Thus, much attention is devoted to experimental determination and computational prediction targeting the global fold of RNA and its local substructures. The latter include multi-branched loops—functionally significant elements that highly affect the spatial shape of the entire molecule. Unfortunately, their computational modeling constitutes a weak point of structural bioinformatics. A remedy for this is in collecting these motifs and analyzing their features.

Results

RNAloops is a self-updating database that stores multi-branched loops identified in the PDB-deposited RNA structures. A description of each loop includes angular data—planar and Euler angles computed between pairs of adjacent helices to allow studying their mutual arrangement in space. The system enables search and analysis of multiloops, presents their structure details numerically and visually, and computes data statistics.

Availability and implementation

RNAloops is freely accessible at https://rnaloops.cs.put.poznan.pl.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

RNA molecules play a significant role in the functioning of living organisms and viruses. They carry out a broad range of functions—from translating genetic information through regulating the activity of genes to catalyzing biochemical reactions. Their participation in diverse processes has made them the center of researchers’ interest for many years (Berg et al., 2002; Miskiewicz et al., 2017). In particular, studies focus on the structure of RNA molecules, trying to bridge the gap between knowledge of the sequences (Kudla et al., 2021; O’Leary et al., 2015; Zok et al., 2022) and how they fold in space (Berman et al., 2000; Blazewicz et al., 2005; Wiedemann and Miłostan, 2017; Zemora and Waldsich, 2010). In recent years, in silico methods for RNA 3D structure prediction have increasingly supported this research by generating spatial prototypes of various RNA molecules (Li et al., 2020). Still, many computationally generated models are far from their native counterparts, as can be observed in subsequent RNA-Puzzles challenges (Cruz et al., 2012; Miao et al., 2015). A detailed analysis of their results allows the identification of weaknesses of the prediction methods (Carrascoza et al., 2022; Lukasiak et al., 2015; Miao et al., 2015; Popenda et al., 2021). They include modeling non-canonical base-pairs, long-range interactions, or selected structure motifs, like n-way junctions, also known as multiloops (Laing and Schlick, 2010; Parlea et al., 2016; Rybarczyk et al., 2015; Zuker and Sankoff, 1984).

n-Way junction in the RNA structure is an internal loop with n outgoing helices, where n$\ge$3. The size of this motif, its 3D shape, and directions of outgoing stems determine the spatial arrangement of various structural elements in the molecule and significantly affect its general fold (Bailor et al., 2011; Hao and Kieft, 2016; Lamiable et al., 2012; Leontis and Westhof, 1998; Lescoute and Westhof, 2006; Parlea et al., 2016; Westhof et al., 1996; Zhao et al., 2012). Our knowledge of multiloops comes primarily from experimentally determined structures deposited in the Protein Data Bank (Berman et al., 2000). Partly, it is also available through databases dedicated to RNA fragments and motifs, such as RNA FRABASE (Popenda et al., 2008), RNA Bricks (Chojnowski et al., 2014), RNA 3D motif atlas (Parlea et al., 2016; Petrov et al., 2013), or RAG-3D (Zahran et al., 2015). These computational resources catalog a wide range of structural elements described with the details common to all motifs’ primary, secondary, and tertiary structures. Multiloops themselves are collected in the RNAJunction database (Bindewald et al., 2008). It stores over 12 000 junctions and kissing loops with annotations covering PDB ID, sequence, tertiary structure, and inter-helix angles and allows searching by PDB ID or RNA sequence. Unfortunately, the database was not updated after 2008 and therefore contains multiloops derived from <30% of the RNA structures currently deposited in PDB. As a result, no complete repository of n-way junctions or their efficient and precise search engine exists. Available bioinformatics systems do not collect multiloop-specific up-to-date data from experimental and computational studies (Bailor et al., 2011; Byron et al., 2013; Hao and Kieft, 2016; Hohng et al., 2004; Hua et al., 2016; Laing et al., 2012; Lescoute and Westhof, 2006). It makes comparative analysis and accurate modeling of these structural motifs difficult or nearly impossible.

Here, we present RNAloops, a database of multi-branched loops identified in the experimental RNA structures from the Protein Data Bank (Berman et al., 2000). The data collected include, i.a. RNA sequence, secondary and tertiary structures, planar and Euler angles (Diebel, 2006) to describe the relationship between outgoing helices. The repository self-updates automatically every week. RNAloops comes with a handy mechanism to query the database contents based on several criteria, for example RNA sequence, secondary structure, the number of branches, and ranges of angle values. It automatically collects statistics about the data in the database and presents them in a user-friendly way. The output is available in text, numeric and graphical form. Retrieved multiloop structures are ready to apply in modeling topologically complex RNAs by the template- and fragment assembly-based prediction methods. They can be used to create learning sets for machine learning-oriented predictors (Townshend et al., 2021), thus, complementing data from the other resources developed for this task (Adamczyk et al., 2022; Becquey et al., 2021). Finally, angular values can control the energy minimization process by constraining the arrangement of branching helices. We believe that due to the systematic collecting of all multiloop-specific data, RNAloops will contribute to improving RNA structure study and modeling.

2 Materials and methods

2.1 Data acquisition into the database

Every week, the RNAloops repository updates with new data taken from the Protein Data Bank (Berman et al., 2000) and supplemented with additional information. The process (see Fig. 1) starts by retrieving PDB IDs of newly deposited, removed, or updated RNA 3D structures. The system downloads the corresponding PDB files in mmCIF format (Bourne et al., 1997). Their contents are standardized using the Biopython functions (Cock et al., 2009): the first model is taken in the case of multimodel files, non-RNA chains and incomplete residues are filtered-out, modified residues are transformed into their non-modified equivalents.

Fig. 1.

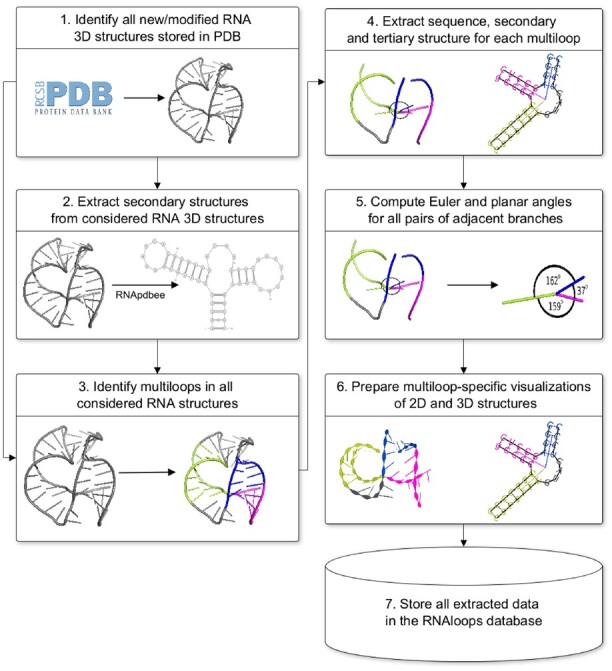
Data flow in the RNAloops database

The secondary structure is derived for each RNA and encoded in extended dot-bracket notation using the RNApdbee algorithms (Antczak et al., 2018a; Popenda et al., 2008). This structure representation is scanned for n-way junctions (n$\ge$3), taking pseudoknot interactions into account. 2D and 3D structures of each identified motif are extracted and uploaded into the database. In the RNAloops system, the structure of a multiloop is described by the loop and the outgoing full-length helices.

The mutual positions of all pairs of adjacent helices protruding from the loop are designated for each multiloop. For this purpose, planar and Euler angles are computed between directional vectors of these helices. The beginning and the end of each vector are in the geometric centers of the multiloop and helix, respectively. The first point is the centroid in the set of all non-hydrogen atoms that belong to the first base pairs of outgoing helices. The second point is based on all non-hydrogens from the third base pair in the helix or the first pair if the helix has <3 bp. Planar angle $\varphi$ (Fig. 2) is computed according to Equation (1) between two directional vectors, $\overrightarrow{a}$ and $\overrightarrow{b}$, projected onto the plane. Euler angles, α, β, and γ (Fig. 2), reflect the orientation of a directional vector to the other. They define rotations to be made about the three coordinate axes to superimpose two helices (Heyde and Wood, 2020). The helix-representing vectors, $\overrightarrow{a}$ and $\overrightarrow{b}$, are projected onto the planes perpendicular to all axes of the coordinate system. An angle between the vectors computes from Equation (1) separately for each dimension.

$$\varphi =\arccos [(\overrightarrow{a}·\overrightarrow{b})/(\left|\overrightarrow{a}\right|·\left|\overrightarrow{b}\right|)]$$ (1)

Fig. 2.

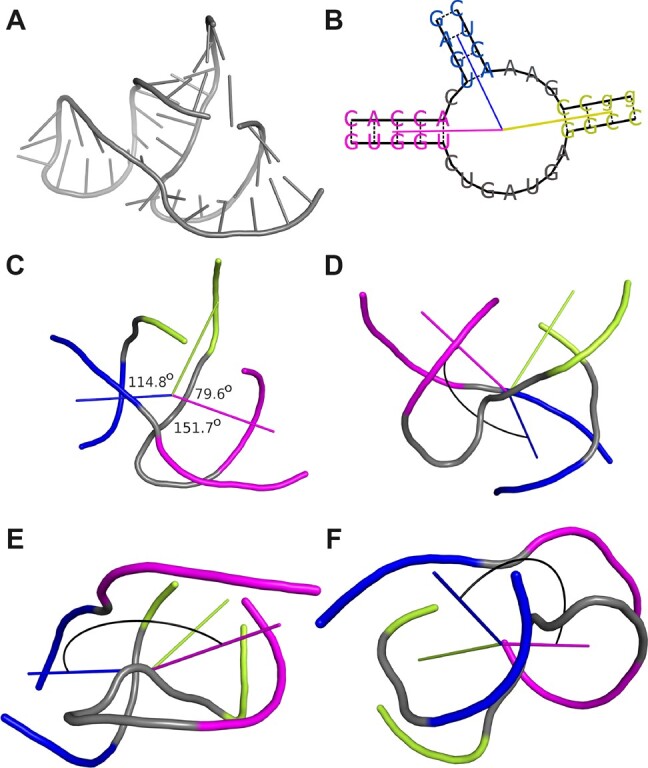
(A) The 3D structure of hammerhead ribozyme (PDB ID: 1NYI; Dunham et al., 2003). (B) The 2D diagram of the three-way junction identified in this structure with the directional vectors plotted. (C) The 3D model of thus junction with planar angle values displayed. Euler angles between the blue and the magenta helix shown from the perspective of the (D) X, (E) Y, and (F) Z axes of the coordinate system, respectively

2.2 The RNAloops system implementation

The RNAloops system consists of a frontend layer providing a user interface, a backend with RESTful API, and the database management and update service. The interface uses React.js and Next.js frameworks and retrieves the searched data via RESTful API. The backend layer executes all user-initiated operations and communicates with the database management and update services. The relational database of RNAloops, operating on PostgreSQL DBMS, is automatically updated weekly. The system is hosted and maintained by the Institute of Computing Science, Poznan University of Technology, Poland.

3 Results

3.1 Database content

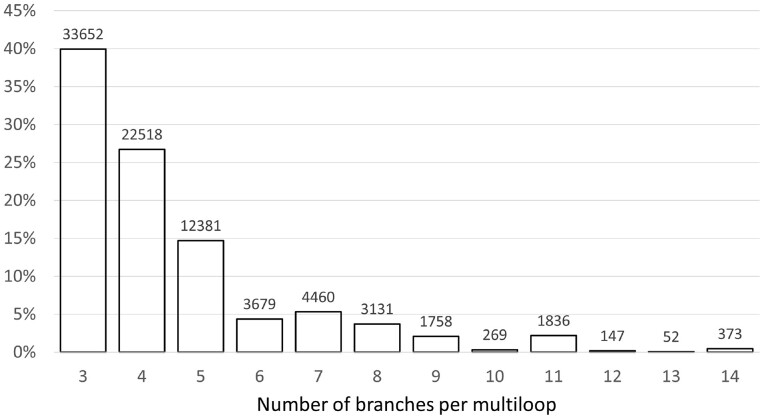
Currently (as of March 31, 2022), RNAloops stores entries for 84 256 multiloops identified in 1831 RNAs from the Protein Data Bank (Berman et al., 2000). We obtained these by processing 5729 RNA-containing structures, that is stand-alone RNAs, RNAs derived from protein–RNA complexes, and DNA–RNA hybrids. Sixty-eight percent of all RNAs examined had no multiloops, whereas 32% contained at least one—these populated the database. They came from structures determined by X-ray (42.6%), fiber diffraction (0.2%), and electron microscopy methods (57.2%). For each of these molecules, we counted how many multiloops it included. The highest proportion (16.37%) is RNAs having exactly two n-way junctions. Structures containing four multiloops constitute 7.14% of the dataset, with 22, 51, and 76 multiloops—3.57%, 1.95%, and 2.23%, respectively. The percentage of structures with other numbers of loops oscillates (for each count) around 0–1%. The collection also includes some RNAs having >100 multiloops. An analysis of n-way junction multiplicity shows the highest number of three-way junctions—they account for nearly 40% of the total collection. The branching multiplicity per multiloop ranges between 3 and 14, but only 0.44% of the motifs have 14 branches. Figure 3 shows the distribution of branching multiplicities in the database.

Fig. 3.

Coverage of the RNAloops dataset by n-way junctions for $n\in <3,14>$

3.2 User interface

RNAloops operates via a web application in any modern web browser. To run it, users open the address https://rnaloops.cs.put.poznan.pl.

The interface consists of five pages: Home, Search result, Help, Statistics, and Cite us. Four of them are visible by default. The Home page enables defining the query to search for data on RNA multiloops. Help explains all the options of web application. In Statistics, users can see stats of current database contents with charts showing data growth and distribution—the total number of RNA structures and multiloops, the number of multiloops by topology, and multiloops by topologies grouped by experimental method or PDB IDs. Statistical data are recomputed automatically after each database update. The Cite us page informs about the RNAloops-related publications. The Search result page displays output data and gets visible when the search completes.

3.2.1 Search modes

The search engine works in two modes: basic and auxiliary. By default, the tab with basic mode opens when entering the RNAloops homepage. It allows defining several search criteria: PDB ID(s), number of branches in a multiloop (specified as a range or exact number), sequence pattern, secondary structure in dot-bracket notation, the range of planar angle values, and ranges of Euler angle values. When searching with an angle criterion, the system returns any multiloop in which at least one angle satisfies the criterion. If several search criteria are defined, the system combines them into a single query and looks for motifs meeting their conjunction. If the users do not enter any criteria and click the Search button, RNAloops outputs the list of all records in the database. The auxiliary mode allows scanning the database for RNAs containing the specified number of n-way junctions. In both modes, users can search hierarchically—the subset resulting from one search can be searched further using the basic mode criteria.

3.2.2 Search results

Basic search outputs the number of items found and their collection divided into pages. By default, each result page displays 10 item tiles. Page capacity is user-adjustable. Each tile contains a thumbnail diagram of the multiloop secondary structure, the type of the loop, and the PDB identifier of the source structure. A detailed description presents by clicking Show details, in four sections. The General information panel contains the multiloop type, a clickable identifier of the source structure linked to the PDB, sequence, and secondary structure in the dot-bracket notation. The file icon in the top right corner allows downloading the PDF file with general information and the details of all components of the multiloop. The right-positioned panel includes sections with the information on multiloop units—branching helices (sequence, length as the number of base pairs, source structure-derived residue numbering), planar and Euler angles between them, and single-stranded connectors (sequence, length as the number of residues, source structure-derived residue numbering). The secondary structure is displayed in two views—with and without directional vectors. The first one (default) is generated using RNAplot (Lorenz et al., 2011) and colored to ease distinguishing multiloop components. To keep clarity, RNAplot does not draw directional vectors if pseudoknotted base pairs are part of the loop. The second view is prepared with VARNA (Darty et al., 2009). Both diagrams are available for download in the Scalable Vector Graphics (SVG) format. The interactive view of the 3D structure is generated using the LiteMol library (Sehnal et al., 2017). The top three buttons allow switching between the structure of the multiloop itself, the source PDB structure, and the source structure with the multiloop highlighted in a different color. Clicking the gear in the 3D window displays the settings panel to manipulate the display parameters. Users can download the 3D structure in mmCIF format (Bourne et al., 1997).

The auxiliary search outputs the number of RNAs found and their list divided into pages. Each structure is described by PDB ID, PDB record title, resolution, experimental method, number of multiloops, and their types. By clicking the item, users get the result page as in the basic search. However, it displays only multiloops included in the selected structure. These results can be processed just like the output from the basic search.

3.3 RNAloops applications

RNAloops enables multi-parametric structural analysis and a search for multiloops meeting user-defined criteria. Such functionalities support, i.a. extracting significant features of structure motifs, their comparative analysis, or 3D structure modeling. Below we present sample applications of the system for three problems—RNA design, determining the spatial shape of an RNA motif based on the similarity of its secondary structure to experimental structures, and homology modeling.

In the first example, we tackled the RNA design problem. It aims to identify RNA sequence(s) that fold to a predefined secondary structure. Here, we targeted the four-way junction discussed in (Ivry et al., 2009). Given the dot-bracket representation of this multiloop secondary structure—(.(-).(-).(-).)—we used the RNAloops search facility to find RNA sequences that could form a loop like this. We ran the search applying strand shifts to include various orientations of the multiloop in the whole molecule context. The system output six four-way junctions—each structure composed of a loop and four branching arms of various lengths (Table 1). The results were ranked based on a global alignment score computed for the loop alone aligned with the target secondary structure. Here, we applied the Needleman–Wunsch algorithm assuming two points for a match, −2 for a mismatch, −1 for a gap (Needleman and Wunsch, 1970). A four-way junction derived from the small-subunit processome (PDB ID: 5WLC) (Barandun et al., 2017) scored the best. Its secondary structure displays the highest similarity to the target with one insertion only. Thus, we obtained the following sequence of a multiloop as the input problem solution: CAGC-GAG-CAC-GGG.

Table 1.

Results of the RNAloops search aimed to find RNA sequences that fold to the target structure

Target secondary structure: (.(-).(-).(-).)
Query	Matching four-way junctions found in RNAloops
	PDB ID(s)	Secondary structure	Sequence	Score
).(-).)	5wlc	(((..(((-))).((-)).(-).)))	UGCAGCUC-GAGAGG-CCAC-GGGCA	23
).(-).(	4v3p	(((((-).(-).(((-))).))))	UCGGG-CUU-AGCAC-GUGUCCGG	21
).(-).)	6spf	((….((-))….((-)).(-).))	ACGAAGGU-GCUUGACU-AGGU-AGGU	18
).(-).(	6q98	((((((((-))))).(-).(-))))	UUGGCCGG-CCGGUUU-GAC-GCAA	18
).(-).(	4u27, 4u1v, 4wf1,	(((((((((((-)))))).(-).(-))))))	UGUUGGCCGGG-CCCGGUUU-GAC-GCAACA	18
	4u25, 4u26, 4u24
(.(-).(	6otr	(.(-).((((((-))))))(-)……………)	UGC-GAGCCGGC-GCCGGCA-UGAACUGGCCGUGAAGA	7

Note: Hits are sorted by a global alignment score computed for the four-way junction secondary structures regardless of the context (i.e. for bolded fragments only). The best one is in the first row of the table.

The second example involves searching for the 3D shape of the RNA motif having specified secondary structure and unknown atomic coordinates. As a target, we selected purine riboswitch (Rfam ID: RF00167) with the secondary structure topology encoded as ((((((…(((((((-)))))))…….(((((((-))))))).)))))). The key motif shaping this molecule’s 3D structure is a three-way junction with a 19-nucleotide internal loop (Barash and Gabdank, 2010). There is no experimental data for such a 2D structure in the Protein Data Bank (Berman et al., 2000). Therefore, querying the RNAloops database for the corresponding dot-bracket input yielded zero results. Following this, we looked for molecules with secondary structures similar (but not the same) to the target. Multiple queries ran separately for each single-stranded component of the three-way junction with and without deletions at unpaired positions. This multi-step procedure resulted in 143 different three-way junctions, which we sorted by the global alignment score (Supplementary Table S1). The best match was a multiloop found in 10 PDB structures. Sorting them by resolution allowed us to select the best solution, a multiloop 3D structure from the Thermus thermophilus 70S ribosome (PDB ID: 4Y4O, 2.30 Å) (Polikanov et al., 2015) (Supplementary Fig. S1).

In the third experiment, we evaluated the utility of RNAloops in modeling the RNA 3D structure. We used the RNAComposer system (Antczak et al., 2016) to predict the core of the Alu domain of mammalian SRP RNA (PDB ID: 1E8O) (Weichenrieder et al., 2000). We first ran the system for sequence and secondary structure data in the default fully automatic mode. The resulting prediction aligned at the reference structure had an RMSD of 4.23 Å. Next, we applied RNAComposer in a semi-automated mode. It allows users to insert particular structural elements into the predicted model. Knowing that multiloops significantly affect the shape of the whole molecule, we decided to model the latter using own three-way junction. To find the best fitting 3D structure for this multiloop, we searched the RNAloops database by giving the secondary structure and loop type as search criteria. We obtained 44 results, and we further reduced this set by excluding motifs originating from the target and those with planar angles outside the range 120°–135°. The remaining three-way junctions were ranked according to the global alignment score computed for their secondary structures (Supplementary Table S2). The best rated multiloop originated from the signal recognition particle interacting with the elongation-arrested ribosome (PDB ID: 1RY1) (Halic et al., 2004). Its 3D structure was extracted from that molecule and used as a structural element in the RNAComposer modeling. The final prediction obtained this way has an RMSD of 2.40 Å. Thus, we improved the modeling accuracy by 56% and confirmed the RNAloops usefulness in RNA 3D structure prediction.

3.4 RNAloops versus other databases

Several existing databases catalog motifs found in experimental RNA 3D structures and make them searchable. They include RNA FRABASE (Antczak et al., 2018b; Popenda et al., 2008), RNA 3D motif atlas (Parlea et al., 2016; Petrov et al., 2013), RNA Bricks (Chojnowski et al., 2014), and RAG-3D (Zahran et al., 2015), which store all kinds of motifs, and RNAJunction (Bindewald et al., 2008) collecting only multiloops. In Table 2, we present the essential features of these resources to assist users in choosing the right fit. They fall into the following groups: supported motif types, database contents, filtering criteria, download options, and other facilities. Four of the six tools cover arbitrary RNA structural motifs. RNAJunction and RNAloops focus on multiloops, facilitating their exploration at the sequence (both), secondary (RNAloops), and tertiary (both) structure levels. The uniqueness of RNAloops includes calculating and sharing angular parameters for neighboring helices protruding out of a loop. RAG-3D, on the other hand, is the only one to show graph-based structure representation. All databases have associated data search engines allowing queries of varying syntax and complexity. Some of the resulting data (e.g. 3D structure in PDB or mmCIF format, graphical 2D and 3D models, structure parameter values) is ready for download with a single click. In the last category, we have included features important for many users—data visualization, self-updating statistics, systematic populating of the database with new data, and secure communication protocol.

Table 2.

Selected features of databases collecting RNA structure motifs

	RNA FRABASE	RNA 3D motif atlas	RNA bricks	RAG-3D	RNAJunction	RNAloops
I Supported RNA motifs	Any	Any	Any	Any	Multiloops	Multiloops
II Database content
Sequence	✓	✓	✓	✓	✓	✓
Secondary structure	✓		✓	✓		✓
Tertiary structure	✓	✓	✓	✓	✓	✓
Graph-based features				✓
Angular data	✓					✓
III Search criteria
PDB ID	✓	✓	✓	✓	✓	✓
Sequence	✓	✓	✓	✓	✓	✓
Secondary structure	✓		✓	✓		✓
Motif topology search	✓		✓			✓
Angular data	✓					✓
IV Download options
Tertiary structure	✓	✓	✓	✓	✓	✓
Other motif-specific data	✓					✓
Table with search results	✓	✓	✓			✓
Visualizations				✓		✓
V Other facilities
Output data visualization			✓			✓
Stats of database contents			✓			✓
Regular data updates	✓	✓	✓	✓		✓
Secure communication (HTTPS)						✓

4 Conclusions

So far, only one database has collected data on RNA multi-branched loops (Bindewald et al., 2008). Unfortunately, it has not been updated since 2008, storing a constant number of ∼12 000 multiloops extracted from RNA structures available at that time. Over the following 14 years, the number of RNAs in the Protein Data Bank has tripled. However, multiloops from newly determined RNA structures were not collected anywhere. The lack of fast and easy access to up-to-date data on these motifs and the need to study them in connection with RNA 3D structure modeling made us design a multiloop-dedicated bioinformatics system. The result of our work is RNAloops, a self-updating database that collects information about multi-branched loops identified in experimental RNA structures. The advantage of the presented tool is that the structural data, which come directly from the PDB, is supplemented with extra information—i.a. Euler angles, planar angles, or branching multiplicities—and visualized in a user-friendly way. Each database update automatically launches a statistical module to provide users with information on data distribution due to various structural parameters. Currently (March 31, 2022), RNAloops contains >84 000 multiloops extracted from 1832 RNAs. The system supports accurate modeling of RNA 3D structures and studying their properties. It complements the collection of RNApolis tools (Szachniuk, 2019) that address various problems of RNA structural studies.

Data Availability

RNAloops is accessible freely at https://rnaloops.cs.put.poznan.pl/ with no login requirements. It can be operated via all modern web browsers.