Abstract

In this paper, we develop a dual-porosity dual-permeability model for binary gas migration to explore the permeability evolution in the matrix and fracture in the process of a gas–water two-phase flow during CO2-enhanced coalbed methane (CO2-ECBM) recovery in coal reservoirs. This mechanistic model accommodates the effects of elastic deformation caused by the effective stress change in the matrix and fracture, the swelling/shrinkage deformation of the matrix caused by adsorption/desorption, the convection and diffusion of gas, and the discharge of water. Specifically, the time-dependent matrix swelling, from initially completely reducing the fracture aperture to finally affecting the coal bulk volume, is considered by the invaded volume fraction involving binary gas intrusion. The model is validated through laboratory data and applied to examine the permeability evolution of CO2-ECBM recovery for 10 000 days. Furthermore, we analyze the sensitivity of some selected initial parameters to capture the key factors affecting CO2-ECBM recovery. Our modeling results show that the permeability evolution can be divided into two stages during the process, where stage I is dominated by effective stress and stage II is dominated by adsorption/desorption. Increasing the injection pressure or initial permeability advances the start of stage II. The decrease in initial water saturation causes the permeability to change more drastically and the time of stage II to appear earlier until a time long enough, after which little effect is seen on the permeability results.
1. Introduction
Coalbed methane (CBM), extracted from coal seams as an alternative fuel to conventional energy sources such as coal, is emerging as a major contributor to an energy-hungry world.1,2 With the increasing prominence of global warming, the goal of achieving “carbon emission peak” and “carbon neutrality” becomes increasingly urgent. The technology of injecting carbon dioxide into the deep unminable coal seams has attracted people’s attention because it can effectively reduce greenhouse gases in the atmosphere and improve the production of coalbed methane and oil and gas recovery rates as well.3,4 More and more laboratory tests and field tests have shown the potential and feasibility of carbon dioxide injection to produce CBM.5−7 However, during the injection of CO2 to enhance CBM, the permeability and porosity that primarily control the production of CBM will change dynamic due to the increase in gas pressure in the reservoir and the higher affinity of CO2 to adsorb onto coal.8 Furthermore, the consideration of the presence of water in the reservoir will complicate the fluid flow in CO2-ECBM production.9 Thus, establishing an accurate and comprehensive permeability model is crucial for CBM recovery and CO2 geological storage.
Recently, a broad variety of works related to the mechanical deformation, sorption/desorption, and transport property of gas on the permeability variation of coal seams were researched.10−21 These permeability models are broadly classified into two types of strain-based models that consider volumetric deformation of the coal and stress-based models that consider geomechanical deformation.22,23 With the advancement of the recognition of physical properties of the reservoir, the conceptual model of naturally fractured reservoirs has been improved from a single-porosity single-permeability model14,24 to a dual-porosity single-permeability (fracture permeability) model,9,25 a dual-porosity dual-permeability model (both matrix and fracture permeability),15,26 and a triple-porosity dual-permeability (both fracture permeability and inorganic permeability).27 The factors affecting reservoir permeability also extend from a single mechanic effect11,28 to adsorption-induced strain effects10,24,29−31 or even coupled with the effect of slip flow.32−37 Modeling the permeability evolution of coal during CBM recovery or CO2-ECBM is an attractive interest area with numerous models being proposed. For instance, Zhou et al.38 investigated the effect of CO2–CH4 interaction on porosity and permeability during CO2-ECBM recovery and developed a related model coupling binary gas flow and coal deformation. Wu et al.15 analyzed the anisotropic evolution of permeability due to gas adsorption and investigated the effects of in situ stresses and fracture aperture on pressure responses during gas production in COMSOL. Fang et al.39 constructed a dynamic permeability prediction model by considering the law of matrix permeability and fracture permeability during CO2-ECBM recovery. Fan et al.9 established a model for the evolution of fracture permeability, considering the THMC coupling of different fields, concluding that neglecting water migration would overestimate gas production and neglecting heat transfer would underestimate gas production.
Admittedly, previous studies have been successful in predicting reservoir permeability to some extent, and there are still gaps in the knowledge of the evolution of reservoir permeability. As the difference in matrix and fracture permeability, the injected gas is only adsorbed near the fracture wall at the beginning, while the swelling strain of the remaining matrix will not change.40−43 The gas diffusion (or invaded) process will continue for a considerable period of time due to the extremely low permeability of the matrix. Therefore, the temporal variability of the invaded region (see Figure 1c–e) will result in a transformation of the swelling strain from an initial local swelling located near the fracture surface that completely reduces the fracture aperture to an eventual global swelling strain that affects the bulk volume.43,44 And this invaded process becomes more complicated owing to the presence of the gas mixture. However, earlier models tend to ignore the matrix permeability without considering the effect of time-dependent swelling on permeability and are even less able to consider this complex gas invasion for CO2-ECBM recovery involving binary gas.
Figure 1.
Conceptual model of coal rock (a, b) and the illustration of the initial equilibrium state to the global invaded state (c–e).
In this paper, coal is considered as a dual-porosity dual-permeability medium based on the true volume of REV; we accurately consider the elastic deformation caused by the effective stress change in the matrix and fracture, the swelling/shrinkage of the matrix caused by the adsorption/desorption effect, and the convection and diffusion of the binary gas in the matrix and fracture. Moreover, the contribution of matrix swelling strain to permeability is quantified by an invaded volume fraction that accounts for the gas intrusion process involving binary gases. In this way, a permeability evolution model coupling solid deformation and fluid flow for a binary gas two-phase flow in gas–water is established. Also, we implement this model onto COMSOL by introducing two new PDE modules to explore the evolution of permeability during the 10 000 day field experiment of CO2-ECBM and then analyze the effects of gas injection pressure, initial water saturation, and initial permeability of the matrix and fracture to capture the key factors that affect CO2-ECBM recovery.
2. CO2-ECBM Model Development
The flow becomes multiphase during CO2-ECBM when groundwater is present in the coal seams. The porosity and permeability affect the flow of water and gas, and the pressure changes caused by the flow of water and gas, in turn, affect the evolution of porosity and permeability. Thus, the establishment of the dynamic permeability evolution model under the combined effects of stress, pressures of water and gas, and adsorption/desorption will be introduced in this section. The basic assumptions in establishing the model are as follows:45
-
(1)
CBM reservoir is a poroelastic medium with dual porosity and dual permeability.
-
(2)
The reservoir temperature is constant.
-
(3)
CO2 and CH4 adsorptions in the CBM reservoir are competitive, both following Langmuir isotherms, and adsorption and desorption only occur in the matrix.
-
(4)
The matrix system only contains the gas phase, and the fracture system contains both the gas and water phases. The two phases are immiscible, and there is no material transfer between the phases.
-
(5)
CO2 and CH4 coexist in the fracture and the matrix, and the free gas conforms to the ideal gas law.
-
(6)
Strain is infinitesimal.
2.1. Concept of Invaded Volume Fraction (IVF)
The gas invaded from the fracture to matrix, during the gas injection process (shown in Figure 1c–e), is very slow, which is usually represented by the invaded volume friction defined as follows43
| 1 |
where a0 is the
initial matrix width (m) and as is the
dynamic invaded depth (m), which is dependent on the diffusivity of
CO2, D2 (m2/s),
and time, t (s), and equals 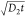 .43 Especially,
the value of finv ranges from 0 to 1 (finv = 1 when as = a/2; finv = 0 when as = 0). The sorption strain of the gas mixture, related
to the properties of each gas component, can be described by an extended
Langmuir isotherm equation9,46
.43 Especially,
the value of finv ranges from 0 to 1 (finv = 1 when as = a/2; finv = 0 when as = 0). The sorption strain of the gas mixture, related
to the properties of each gas component, can be described by an extended
Langmuir isotherm equation9,46
 |
2 |
where i is 1 or 2, and subscripts 1 and 2 represent CH4 and CO2, respectively; εms represents the matrix swelling strain caused by adsorption/desorption. Subscript 0 represents the initial state, εL is the Langmuir-type strain coefficient, and bi = 1/pLi(1/Pa). When injecting CO2 into the coalbed methane reservoir, we assumed that the matrix volume of the invaded segment contains the CO2, and the uninvaded matrix volume contains the CH4 only. The matrix strain increment induced by the gas invading process is
| 3 |
where pm is the gas pressure of the matrix (Pa), and subscripts 1 and 2 represent the pressure induced by CH4 and CO2, respectively. Since the sorption strain of the matrix partly corresponds to the bulk strain and the remaining contributes to the reduction of the fracture,17,47 we can address the matrix sorption strain increment as finv Δεms (corresponding to the bulk strain) and (1 – finv) Δεms (corresponding to the fracture aperture)
| 4 |
And the increment of bulk volume and the reduction of fracture volume caused by matrix sorption can be expressed as
| 5 |
| 6 |
The matrix volume increment induced by adsorption is
| 7 |
where Vm0 is the initial matrix volume (m3).
Therefore, the relationship between the bulk swelling strain increment and matrix swelling strain increment can be known from the definition of the bulk swelling strain increment
| 8 |
where Vb0 and Vf0 are the initial volume of coal bulk and fracture (m3), respectively.
2.2. Permeability Evolution Model Based on IVF
We consider CBM reservoirs as dual elastic media in Figure 1. The effective stress, following the effective stress principle,48 can be expressed as
| 9 |
where subscripts m and f represent the matrix and fracture, respectively, p represents the gas pressure in the pores (Pa), σ represents the mean principal stress (Pa), α = 1 – K/Km, γ = 1 – Kf/Km are the Biot coefficients for the matrix and fracture, respectively, and K, Km, and Kf are the bulk modulus of the dual-porosity media, the matrix and fracture system (Pa), respectively.
2.2.1. Fracture Permeability
The gas pressure of the unreacted binary mixed gas follows Dalton’s law and can be expressed as46
| 10 |
where subscripts 1 and 2 represent the gas pressure caused by CH4 and CO2, respectively. Under the condition of robustly considering the elastic deformation of the matrix and fracture and the adsorption/desorption effect, we can express the coal volume strain Δεv as27
| 11 |
where s is the fracture spacing (m), Δσem and Δσef are the change of the effective stress of matrix and fracture (Pa), respectively, and Δεbs is the bulk swelling strain. Combining eqs 9–10 and rewriting eq 11, we can obtain
| 12 |
As Km is several magnitudes larger than Kf (1/Kf – 1/Km≈1/Kf), eq 12 can be simplified to
| 13 |
According to the relationship between the volumetric strain and linear strain in the theory of elasticity, we obtain the change in fracture aperture Δb (m) as
| 14 |
Then, the fracture porosity ϕf can be expressed as
| 15 |
Solving eqs 13–15, the porosity model of the fracture is
| 16 |
Based on the cubic law, the fracture permeability evolution model is
| 17 |
where the terms in parentheses on the right express the contributions to the fracture permeability from fluid pressure, adsorption, and mechanical deformation, respectively.
2.2.2. Matrix Permeability
According to eqs 9 and 12, the effective stress change in the matrix can be expressed as
| 18 |
Assuming that the matrix volume is Vm (m2) and the matrix pore volume is Vp (m2), the matrix porosity may be written as
| 19 |
| 20 |
Therefore, integrating both sides of the equation and taking the natural exponent of the results leads to
| 21 |
The volumetric change of the matrix is determined by the combined effect of effective stress and adsorption/desorption. When the matrix volume varies, the matrix pore also changes accordingly. Taking the effective stress and adsorption/desorption into consideration, we can define the volumetric strain for the matrix as
| 22 |
Considering that the modulus of coal strain Ks is several magnitudes larger than the modulus of the matrix Km (1/Ks + 1/Km≈1/Km), the change of pore volume strain, associated with the matrix global strain and pore local strain,26 can be rewritten as
| 23 |
Substituting eqs 18, 22, and 23 into eq 21, the porosity model of the matrix is
| 24 |
Again, taking the cubic law, the evolution of matrix permeability can be expressed as
 |
25 |
From eq 25, we can acknowledge that the evolution of permeability is a function of mechanical deformation, induced from the change in stress and fluid pressure, and adsorption deformation, corresponding to the gas invaded.
2.3. Fluid Migration Model
In developing the fluid transport models for the balance equation of each component, we formulate the following assumptions: (1) the laminar flow of binary mixed gas in matrix pores or fracture obeys Darcy’s law and (2) the diffusion of the binary gas mixture between the matrix and fracture follows Fick’s law. For the matrix system, the basic variable is the gas pressure. For the fracture system, the basic variables are gas pressure and water saturation, whereas water pressure is a function of gas pressure and water saturation.
2.3.1. Matrix Flow Equation
The equilibrium equation in the matrix system contains convection and diffusion, and it also includes the conversion between free gas and adsorbed gas. The premise of the equation is that the gas flow is affected by both the pressure field (Darcy’s law) and the concentration field (Fick’s law); therefore, the velocities are added. The equation can be written as1,49
| 26 |
where mmi represents the gas content in the matrix including free gas and adsorbed gas (kg/m3), and subscript i represents the gas of different components; ρmi is the gas density of component i with a relationship with the gas pressure as ρmi = βipmi (kg/m3), βi = Mi/RT, Mi is the relative molecular mass (kg/mol), and T is the reservoir temperature (K). The second term represents the advective flux related to the gas phase. The third term represents the nonadvective flux corresponding to gas diffusion. The mmi of each component can be expressed as50
| 27 |
where ρs is the reservoir density (kg/m3), ρgai is the gas density under standard conditions (pa = 0.103MPa), and vmi is the advective velocity of gas migration in the matrix considering the Klinkenberg effect (m/s), which can be expressed as51
| 28 |
where bk is the Klinkenberg coefficient and μm is the viscosity of the mixed gas in the matrix pores, which can be expressed as27
| 29 |
where μi is the gas viscosity (Pa·s) and Di is the dynamic diffusion coefficient (m2/s), which can be defined as
| 30 |
Qgmf is the gas exchange between the matrix and fracture, which may be expressed as
| 31 |
where w = 8 (1 + 2/a2) km/μm is the transfer coefficient between the matrix and fracture.15,50,52 Combining eqs 26–31, the expressions of gas migration of different components in the matrix are obtained.
For CH4
 |
32 |
For CO2
 |
33 |
2.3.2. Fracture Flow Equation
The coal fracture system contains binary gas and liquid water; hence, two mass conservation equations are needed.1,53 The governing equations for gas and water can be defined as
| 34 |
| 35 |
where subscript w indicates water, and mfi and mw represent the quality of gas and water in the fracture system (kg/m3), respectively, which can be described as
| 36 |
| 37 |
where Sw and Sg represent the saturation of water and gas, respectively, and Sg = 1 – Sw.54 ρw represents the density of water (kg/m3). vfg and vw represent the gas velocity and water velocity of the fracture (m/s), respectively. Based on Darcy’s law, which can be described as9
| 38 |
| 39 |
where pw represents water pressure (Pa), and kfe and kwe represent the effective permeability of gas and water in the fracture system (m2), respectively. Water pressure and the actual permeability of gas and water expressed in terms of effective permeability55 can be described as
| 40 |
| 41 |
where pc is the capillary pressure (Pa), pg represents the gas pressure (Pa), krg0 and krw0 represent the end-point relative permeability of gas and water (m2), respectively, and krg and krw represent the relative permeability of gas and water (m2), respectively. The capillary pressure and relative permeability model proposed by ref (56) are expressed as
| 42 |
| 43 |
where pe is the entry capillary pressure (Pa), λ is a function related to the pore size distribution, m is the relative permeability coefficient, and se is the effective saturation, expressed as
| 44 |
where Swr is the irreducible water saturation, Sgr is the residual gas saturation, μw is the viscosity of water (Pa·s), and μf is the viscosity of mixed gas in the fracture system (Pa·s), which can then be written as
| 45 |
Combining eqs 34–45 yields the balance equation as the following.
For CH4
 |
46 |
For CO2
 |
47 |
For water
| 48 |
2.4. Deformation Equation
Considering the influence of formation pressure change on reservoir deformation, the Navier equation of a dual-porosity medium can be expressed as50
| 49 |
where G is the shear modulus (Pa), u is the displacement (m), ν is Poisson’s ratio, and f is the body force (N). The gas flow equations of CH4 and CO2 (eqs 32–33), mass conservation equations of CH4, CO2, and water (eqs 46–48), and deformation equation of formation (eq 49) together make up the multifield coupling model for dual-porosity media.
3. Model Validation
To verify the suitability and feasibility of this model, we compare our model with the experimental data5 and Fan’s model9 that of CO2-ECBM under various injection pressures. The experiment was conducted at Chongqing University using coal samples recovered from the C1 coal seam in the Baijiao Coal Mine, Nanchuan Basin, China. Cylindrical coal samples had a diameter of 48.3 mm and a height of 98.2 mm. During the experiment, the temperature was set to 15 °C and the confining stress and axial stress were 6 MPa and 8 MPa, respectively. At the beginning of the experiment, CH4 was injected under a constant gas injection pressure of 1.5 MPa to ensure gas pressure equilibrium in the sample. Then, under the constant confining stress and axial stress, CO2 injection pressures of 2, 2.5, 3, and 3.5 MPa were applied at the top of the samples, and the pressures of CO2 and CH4 at the bottom outlet were kept at the atmospheric pressure. The initial CH4 pressure of the coal sample is 1.5 MPa. All of the relevant parameters are listed in Figure 2a–d; most of them are obtained from the original research5 and the related papers,9,15,27 while the rest are obtained by fitting experimental data. Results in Figure 2 indicate that our model is in good agreement with the experimental data at different injection pressures, and the fit is better under the conditions of higher gas injection pressure than the lower. The seepage problem in the matrix–fracture of coal in our model is a bimodal pore system model, and the adsorption deformation is considered time-dependent. Thus, the flow rate of CH4 within the coal is more sensitive to the deformation than Fan’s model.
Figure 2.
Comparison of our model with test data5 and Fan’s model9 at various injection pressures: (a) 2 MPa, (b) 2.5 MPa, (c) 3 MPa, and (d) 3.5 MPa.
4. CO2-ECBM Numerical Simulation
4.1. Model Description
To investigate the permeability evolution during a gas–water two-phase flow in the CO2-ECBM mining of coal reservoirs, we build a 150 m × 150 m × 5 m model (see Figure 3b), which belongs to the upper right quadrant of a traditional five-point well configuration,57 as shown in Figure 3a. The well diameter is 0.1 m for injection well (IW) and production well (PW). For the geomechanics boundary conditions, the left and bottom are zero-displacement-constrained, and in situ stress is applied on the top and right boundaries. For the gas flow boundary conditions, the bottom-hole pressures for PW and IW are 0.1 and 8 MPa, respectively, and the other boundaries are defined as no flow. As for the water flow boundary conditions, the pressures for PW and IW are the same as the gas flow boundary conditions; however, the IW and Pw are set as the Dirichlet boundaries with the prescribed values of Sw are 0 and 0.82, respectively.
Figure 3.
(a) Illustration of the five-point well for the CO2-ECBM test and (b) model geometry for CO2-ECBM simulation.
The initial pressure of methane in the reservoir is 5.24 MPa, the initial pressure of carbon dioxide is set to be 0.1 MPa, the temperature is 338.8 K, the initial water saturation is 0.82, and the initial permeability is km = 1 × 10–17 m2, kf = 1 × 10–14 m2. Other parameters required for simulation are listed in Table 1, as obtained from the literature.5,9,15,27,39,58 The in situ stress of the reservoir is σy = σx = 6 MPa, and the simulations are run for 10 000 days. There are three reference points A (37, 37), B (75, 75), and C (113, 113) for simulation; we will analyze them in detail in the following section.
Table 1. Input Parameters Used in the Numerical Simulation.
| parameter | value | parameter | value |
|---|---|---|---|
| matrix width, a (m) | 0.01 | Langmuir constant of CH4-induced strain, εL1 | 0.0128 |
| fracture aperture, b(m) | 0.0002 | Langmuir constant of CO2-induced strain, εL2 | 0.0237 |
| initial permeability of the matrix, km0 (m2) | 1 × 10–17 | Langmuir volume constant of CH4, VL1 (m3/kg) | 0.0256 |
| initial permeability of the fracture, kf0 (m2) | 1 × 10–14 | Langmuir volume constant of CO2, VL2 (m3/kg) | 0.0477 |
| porosity of the matrix, ϕm0 | 0.045 | Langmuir pressure constant of CH4, PL1 (MPa) | 2.07 |
| porosity of the fracture, ϕf0 | 0.011 | Langmuir pressure constant of CO2, PL2 (MPa) | 1.38 |
| density of coal, ρs (kg/m3) | 1.47 × 103 | initial water saturation, Sw0 | 0.82 |
| bulk modulus of the matrix, Km (Pa) | 1.2 × 1010 | irreducible water saturation, Swr | 0.42 |
| bulk modulus of the fracture, Kf (Pa) | 1.5 × 108 | residual gas saturation, Sgr | 0.05 |
| Young’s modulus of coal seam, E (GPa) | 4 | dynamic viscosity of CH4, μ1 (Pa·s) | 1.34 × 10–5 |
| temperature, T (K) | 338.8 | dynamic viscosity of CO2, μ2 (Pa·s) | 1.84 × 10–5 |
| coefficient, η | 1 | dynamic viscosity of water, μw (Pa·s) | 1.01 × 10–3 |
| Klinkenberg factor, bk (MPa) | 0.76 | diffusion coefficient of CH4, D10 (m2/s) | 3.6 × 10–12 |
| entry capillary pressure, pe (MPa) | 0.1 | diffusion coefficient of CO2, D20 (m2/s) | 5.8 × 10–12 |
| capillary pressure model: coefficient, λ | 2 | relative permeability model coefficient, m | 0.6 |
| Poisson’s ratio, ν | 0.35 | In situ stress of reservoir, σ (MPa) | 6 |
4.2. Simulation Results
We analyze the changes in gas pressure, permeability, and reservoir deformation of the matrix and fracture at different locations under the two-phase flow environment. The schematic in Figure 4 shows the key factors that could affect gas production behavior. As we all know, the injection of CO2 and the production of CH4 change the gas pressure, causing effective stress changes and adsorption/desorption to occur, which affects the evolutions of porosity and permeability of the reservoir. At the same time, the drainage alters the effective pore size for the gas flow in the fracture. Changes in the gas flow rate will also affect the changes in gas pressure, which, in turn, affects permeability. In the following, we will analyze the evolution of permeability and its mechanisms in detail by examining the pressure, strain, and methane and carbon dioxide contents of the reservoir.
Figure 4.
Key factors affecting permeability evolution in the matrix and fracture for CO2-ECBM simulation.
Figure 5 shows the relationship between gas volume invaded friction (finv) and time during the process of CO2-ECBM. It is worth mentioning that this time is not the duration of mining, but the time during which CO2 arrives in a certain area and fully invades it. The finv increases with time, and the value ranges from 0 to 1. This means the matrix swelling strain from initially reducing the fracture aperture (finv = 0) to eventually affecting the bulk volume strain (finv = 1). The process of CO2 invading the matrix takes about 100 days.
Figure 5.

Evolution of the gas invaded volume fraction versus time.
4.2.1. Gas Pressure
Figure 6 shows the evolution of gas pressures in the matrix and fracture at A–C locations during the simulation period. Within the first 10 days, we clearly observe that the matrix gas pressure change occurs later than the fracture at the beginning. This phenomenon occurs because the gas exchange between the matrix and the outside world occurs through the fracture system. In addition, the pressure changes in the matrix and fracture show a common phenomenon; that is, in the beginning, the pressure at point A increases as CO2 is injected; the pressure at point C decreases with the production of methane. At about 100 days, the increase of CO2 at point B will cause the pressure to increase; however, the pressure increase at point C is more likely caused by the gas desorption from coalbed since the CO2 has not traveled to this part. As the process continues, the pressure will reach a peak value and begin to decrease due to the long-term production of CH4.
Figure 6.
Evolution of gas pressure in the matrix and fracture system during CO2-ECBM: (a) gas pressure in the matrix and (b) gas pressure in the fracture.
4.2.2. Permeability
The permeability evolution contours in the simulated area are shown in Figure 7. We find that the change in permeability is most pronounced during the first 3000 days of the CO2 injection process. The permeability of the matrix and fracture evolves in a similar manner. That is, the reduction in distance from the IW enhances the permeability. In contrast, the permeability decreases with distance from the PW. The permeability change of the fracture is more profound with greater reduction compared with the matrix permeability. To understand how permeability evolves more intuitively, we plot the change of permeability over time at reference points, as shown in Figure 8.
Figure 7.
Evolution of coal matrix and fracture permeability rate in the model during CO2-ECBM.
Figure 8.
Evolution of the permeability ratio at three reference points (A, B, C) during CO2-ECBM: (a) matrix permeability ratio and (b) fracture permeability ratio.
After the permeability at point A reaches the peak point M, it enters stage II and the net permeability starts to decrease, as illustrated in Figure 8. Due to the extra low porosity of the reservoir, the injected gas diffusing from IW to PW will take a long time. Therefore, the time of permeability evolution to stage II increases with the distance from IW, that is, point B is about 100 days, and point C is about 500 days. Permeability in stage I is mainly controlled by effective stress, while in stage II, it is primarily affected by gas adsorption/desorption. Importantly, both adsorption and desorption exist in the process of CO2 replacing CH4. Since the Langmuir volume constant of CO2 is larger than CH4, as a result, the expansion caused by CO2 adsorption is larger than the contraction caused by the desorption of CH4. Furthermore, the influencing factors on permeability evolution at point C are more complicated. With reference to Figure 6, the increase in the matrix and fracture pressure causes the effective stress to decrease, resulting in an increase in porosity and permeability. Concurrently, the increased pressure leads to CO2 adsorption and CH4 desorption and associated swelling/shrinkage strains. When the CO2 content is sufficient, the adsorption strain is greater than the desorption strain (Figure 9 shows increased adsorption strain); hence, the process is considered to be matrix expansion. The expansion of the matrix narrows the fracture aperture, which also compresses the matrix pores, so that the permeability of the matrix and the fracture tend to decrease. The result of the competition between these two processes causes the net permeability to decline.
Figure 9.

Adsorption-induced strain at three reference points (A, B, C) during CO2-ECBM.
4.2.3. Gas Content
The evolution of CH4 and CO2 gas contents (kg/m3) in the simulated area is shown in Figure 10. The CH4 content is always centered around the PW, and it gradually increases toward the IW. Conversely, the CO2 content is always centered around the IW and gradually decreases toward the PW. Following, we draw a straight line from the IW to the PW and plot a function between the gas content and distance away from the IW at different times, as shown in Figure 11. It can be seen that, at all times, the farther away from the IW, the lower the gas content. Gas contents in the vicinity of PW drop sharply. As CO2 injection continues, the methane gas content in the simulated area keeps decreasing, and the carbon dioxide content keeps increasing. A larger degree of change is seen in the first 3000 days. Figure 12 shows the CH4 production rate, CO2 injection rate, and water production rate during the 5000 days of injection. During the first 1000 days, the water production rate declines exponentially. Therefore, the reduction of water saturation in the fracture system increases the effective gas permeability and the flow rate, so the gas production rate continues to increase. At about 1000 days, the water production rate basically reaches the minimum value, while the gas production rate reaches the maximum value. For the storage of CO2, the injection rate reaches the maximum within a short time and is then followed by a downward trend. This is because the CO2 pressure increases rapidly near the IW in a short time. However, due to the low effective gas permeability, CO2 cannot reach deep into the reservoir within a short time, resulting in the accumulation of CO2 around the IW, which limits the pressure differential between the inside and outside of the IW and thus reduces the carbon dioxide storage rate. As drainage progresses, the gas migration path in the fracture increases and the gas velocity increases. Therefore, as CO2 around the IW migrates further into the reservoir, we observe an increased CO2 injection rate until it reaches the second, but relatively small, peak.
Figure 10.
Distribution of CH4 and CO2 contents in the model during CO2-ECBM.
Figure 11.

Variation of CH4 and CO2 contents in the reservoir with the distance away from the gas injection well.
Figure 12.

Water and gas production rates and CO2 injection rate during CO2-ECBM.
5. Results and Discussion
We will discuss how the key factors impact reservoir performance in this section. These factors include carbon dioxide injection pressure, initial water saturation, and initial permeability of the matrix and fracture system.
5.1. Injection Pressure
Taking A and C as reference points, it is known from the discussions above that permeability evolution depends on two competing processes: effective stress and adsorption/desorption. Changing CO2 injection pressure can affect the changes of the two processes simultaneously. Therefore, we perform research on the evolution of permeability at different locations when the CO2 injection pressure is 4, 6, and 8 MPa.
The effects of different injection pressures on permeability and adsorption are demonstrated in Figures 13 and 14, respectively. Figure 13 indicates that under the same gas injection pressure, the permeability evolution of the matrix and fracture is similar: the higher the gas injection pressure, the more dynamic the permeability evolution. For the same position, we find that stage I of permeability evolution will end up earlier at higher injection pressure. Moreover, the permeability at about 10 000 days will decrease with the increasing injection pressure. And the difference in permeability values at different locations will become smaller with the higher injection pressure. In the case of higher injection pressure, the permeability peak appears earlier and stage II starts earlier due to the lower effective stress at point A. In addition, we find that the evolution of permeability at point C is almost opposite to that at point A when using different gas injection pressures. In Figure 13, the permeability at point C of stage I increases with the decreasing injection pressure, and from the beginning of stage II (point E) to equilibrium state, the permeability ends up higher at the lowest injection pressure. The mechanism of this phenomenon is that higher injection pressure will increase the pressure in coal seam; thus, the adsorption swelling of CO2 will exceed the desorption of CH4, leading to a lower permeability. Figure 14 shows that the desorption at point C is negatively correlated with the gas injection pressure. In other words, when the gas injection pressure decreases, the maximum strain caused by desorption increases. Therefore, it can be inferred that from the beginning of stage II to point E, the desorption has a dominant influence on permeability.
Figure 13.
Permeability evolution at reference points A and C with different gas injection pressures (E is the deflection point of adsorption/desorption) during CO2-ECBM: (a) matrix permeability ratio and (b) fracture permeability ratio.
Figure 14.

Adsorption strain at reference point C under different injection pressures during CO2-ECBM.
5.2. Initial Water Saturation
In this work, the initial water saturations of 0.64, 0.74, and 0.84 are considered to explore the effects of different initial water saturations on the evolution of permeability. Figure 15 illustrates that the smaller the initial water saturation, the higher the peak matrix and fracture permeability at point A and the lower the permeability at point C in the first 100 days. Combining with the adsorption strain at points A and C in Figure 16, obviously, the lower initial water saturation of reservoir, the earlier adsorption occurs, and the higher water saturation will limit gas adsorption to enhance the permeability. However, as the injection continues long enough, the permeability tends to be independent of water saturation and equal to the equilibrium state. Similarly, after a sufficient period of time, the adsorption strains show no dramatic difference. Figure 17 displays the effect of the initial water saturation of the reservoir on gas migration. We find that faster migration is associated with lower initial water saturation until a certain time. A higher water saturation will occupy more flow channels and reduce the percentage of gas content before the system equilibrates.
Figure 15.
Permeability evolution at reference points A and C with different initial water saturations during CO2-ECBM: (a) matrix permeability ratio and (b) fracture permeability ratio.
Figure 16.

Adsorption-induced strain at reference points A and C under different initial water saturations during CO2-ECBM.
Figure 17.

Variation of CH4 and CO2 content percentages at reference points A and C with different initial water saturations.
5.3. Initial Permeability
Reasonable values of the initial permeability of the matrix and fracture in three cases are selected within the range of available literature to examine the effect of initial reservoir permeability on the gas migration performance, and the input parameters for these cases are summarized in Table 2. The evolution of the matrix and fracture permeability at different initial permeability values is shown in Figure 18. We can see that the initial permeability has a significant impact on gas migration. As the initial permeability decreases, stage II occurs late and the final decrease in permeability becomes smaller. The reason for this is that the smaller the initial permeability, the later the adsorption occurs near the production well, as shown in Figure 19. Consequently, a smaller adsorption strain causes a smaller decrease in permeability. The difference in initial permeability, however, has little effect on the degree of change in the matrix and fracture permeability at different locations, as shown in Figure 18, where three cases are plotted with the same ΔkmL/ΔkfL.
Table 2. Initial Permeability of Matrix and Fracture in Three Cases Used for Sensitivity Analysis.
| case | matrix (m2) | fracture (m2) |
|---|---|---|
| Case 1 | 10–17 | 10–14 |
| Case 2 | 5 × 10–18 | 5 × 10–15 |
| Case 3 | 1 × 10–18 | 1 × 10–15 |
Figure 18.
Permeability evolution at reference points A and C under three different initial permeabilities during CO2-ECBM: (a) matrix permeability ratio and (b) fracture permeability ratio.
Figure 19.

Adsorption-induced strain at reference points A and C under three different initial permeabilities during CO2-ECBM.
In Figure 20, the ratio between methane and carbon dioxide concentration is plotted. It is found that the increase in initial permeability has accelerated the gas migration rate in the reservoir, and methane production and carbon dioxide storage have also increased during the same period. Clearly, it is important to take measures to increase the reservoir permeability before gas production in the field.
Figure 20.

Variation of CH4 and CO2 content percentages at reference points A and C under three different initial permeabilities.
6. Conclusions
We developed a multifield-coupled two-phase permeability evolution model by accurately taking into account the elastic deformation caused by the effective stress change in different media (matrix and fracture), the swelling/shrinkage deformation of the matrix caused by the adsorption/desorption effect, and both convective and diffusive flows in the matrix and fracture. Then, we verified the fidelity of our model by comparing against experimental data and applying it to a CO2-ECBM field case. A comprehensive analysis of permeability evolution during 10 000 days of CO2-ECBM was performed. Furthermore, we conducted a sensitivity analysis on three initial parameters including initial water saturation, initial permeability, and gas injection pressure. The following conclusions can be drawn from this study:
-
(1)
Significant difference exists in permeability evolution between the area near the IW and PW in the reservoir. This is the result of the combined effect of effective stress and adsorption/desorption. Therefore, it is very important to fully consider the permeability evolution at different locations in the entire area during CO2-ECBM recovery. The permeability evolution process at any location can be approximately divided into two stages, and each stage is affected by the effective stress and adsorption/desorption to different degrees. In stage I, permeability is mainly dominated by effective stress, and in stage II, it is mainly dominated by adsorption/desorption.
-
(2)
The higher the gas injection pressure, the greater the difference in permeability at different locations in the reservoir, and the lower the permeability at the same location. In addition, high injection pressure creates a faster gas migration velocity and a lower effective stress, which causes stage II of permeability evolution to appear earlier.
-
(3)
The water in the reservoir has a negative effect on gas migration. Larger initial water saturation of the reservoir slows down the gas migration rate, resulting in delayed adsorption. Decreasing the initial water saturation causes the permeability of the matrix and fracture to change drastically and also causes stage II of permeability evolution to appear earlier. However, the difference in initial water saturation has a negligible effect on the reservoir performance when the injection time is long enough.
-
(4)
The initial coal permeability has a great influence on the gas migration in the reservoir. Decreasing the initial permeability leads to a slower gas migration rate and delays the time for adsorption to take effect, which decreases the adsorption-induced strain. In addition, it also delays the start of stage II of permeability evolution and reduces the magnitude of decrease in permeability within the same amount of time.
Acknowledgments
This work was supported by the “Natural Science Foundation of China” (52079077). The source of support was gratefully acknowledged.
The authors declare no competing financial interest.
References
- Kumar H.; Elsworth D.; Mathews J. P.; Liu J.; Pone D. Effect of CO2 injection on heterogeneously permeable coalbed reservoirs. Fuel 2014, 135, 509–521. 10.1016/j.fuel.2014.07.002. [DOI] [Google Scholar]
- Rundgren E. J. Coal-Bed Methane Provides Less-Invasive Production Method. Nat. Gas. Electr. 2016, 33, 22–25. 10.1002/gas.21937. [DOI] [Google Scholar]
- Godec M.; Koperna G.; Gale J. CO2-ECBM: a review of its status and global potential. Energy Procedia. 2014, 63, 5858–5869. 10.1016/j.egypro.2014.11.619. [DOI] [Google Scholar]
- Zheng S.; Yao Y.; Elsworth D.; Liu D.; Cai Y. Dynamic Fluid Interactions during CO2-Enhanced Coalbed Methane and CO2 Sequestration in Coal Seams. Part 1: CO2–CH4 Interactions. Energy Fuels 2020, 34, 8274–8282. 10.1021/acs.energyfuels.0c01371. [DOI] [Google Scholar]
- Yin G.; Deng B.; Li M.; Zhang D.; Wang W.; Li W.; Shang D. Impact of injection pressure on CO2–enhanced coalbed methane recovery considering mass transfer between coal fracture and matrix. Fuel 2017, 196, 288–297. 10.1016/j.fuel.2017.02.011. [DOI] [Google Scholar]
- Deng B.; Yin G.; Zhang D.; Li M.; Liu Y.; Lu J. Experimental investigation of fracture propagation induced by carbon dioxide and water in coal seam reservoirs. Powder. Technol. 2018, 338, 847–856. 10.1016/j.powtec.2018.07.071. [DOI] [Google Scholar]
- Mazzotti M.; Pini R.; Storti G. Enhanced coalbed methane recovery. J. Supercrit. Fluids 2009, 47, 619–627. 10.1016/j.supflu.2008.08.013. [DOI] [Google Scholar]
- Wu Y.; Liu J.; Elsworth D.; Chen Z.; Connell L.; Pan Z. Dual poroelastic response of a coal seam to CO2 injection. Int. J. Greenhouse Gas Control 2010, 4, 668–678. 10.1016/j.ijggc.2010.02.004. [DOI] [Google Scholar]
- Fan C.; Elsworth D.; Li S.; Zhou L.; Yang Z.; Song Y. Thermo-hydro-mechanical-chemical couplings controlling CH4 production and CO2 sequestration in enhanced coalbed methane recovery. Energy 2019, 173, 1054–1077. 10.1016/j.energy.2019.02.126. [DOI] [Google Scholar]
- Gray I. Reservoir engineering in coal seams: part 1-the physical process of gas storage and movement in coal seams. SPE Reserv. Eng. 1987, 2, 28–34. 10.2118/12514-PA. [DOI] [Google Scholar]
- Seidle J. P.; Jeansonne M. W.; Erickson D. J.. Application of Matchstick Geometry to Stress Dependent Permeability in Coals, Proceedings of the SPE Rocky Mountain Regional Meeting; Casper, WY, May 18–21, 1992.
- Palmer I.; Mansoori J.. How Permeability Depends on Stress and Pore Pressure in Coalbeds: A New Model, Annual Technical Conference and Exhibition, Denver, CO, Oct. 6–9, 1996, SPE 24361.
- Shi J. Q.; Durucan S. Drawdown induced changes in permeability of coalbeds: a new interpretation of the reservoir response to primary recovery. Transport. Porous. Med. 2004, 56, 1–16. 10.1023/B:TIPM.0000018398.19928.5a. [DOI] [Google Scholar]
- Zhang H.; Liu J.; Elsworth D. How sorption-induced matrix deformation affects gas flow in coal seams: a new FE model. Int. J. Rock. Mech. Min. 2008, 45, 1226–1236. 10.1016/j.ijrmms.2007.11.007. [DOI] [Google Scholar]
- Wu Y.; Liu J.; Chen Z.; Elsworth D.; Pone D. A dual poroelastic model for CO2-enhanced coalbed methane recovery. Int. J. Coal. Geol. 2011, 86, 177–189. 10.1016/j.coal.2011.01.004. [DOI] [Google Scholar]
- Wu K.; Li X.; Guo C.. et al. Adsorbed Gas Surface Diffusion and Bulk Gas Transport in Nanopores of Shale Reservoirs with Real Gas Effect Adsorption-mechanical Coupling, SPE Reservoir Simulation Symposium, Houston, TX, USA, Feb. 23–25, Society of Petroleum Engineers: Richardson, TX, USA, 2015, SPE 173201.
- Liu T.; Lin B.; Yang W. Impact of matrix–fracture interactions on coal permeability: model development and analysis. Fuel 2017, 207, 522–532. 10.1016/j.fuel.2017.06.125. [DOI] [Google Scholar]
- Wang G.; Xiao Z.; Yu J.; Zhang L.; Sun L. An improved coal permeability model with variable cleat width and Klinkenberg coefficient. Geotech. Geol. Eng. 2020, 38, 3041–3051. 10.1007/s10706-020-01205-9. [DOI] [Google Scholar]
- Jiang C.; Zhao Z.; Zhang X.; Liu J.; Elsworth D.; Cui G. Controlling effects of differential swelling index on evolution of coal permeability. J. Rock. Mech. and Geotech. 2020, 12, 461–472. 10.1016/j.jrmge.2020.02.001. [DOI] [Google Scholar]
- Du X.; Cheng Y.; Liu Z.; Yin H.; Wu T.; Huo L.; Shu C. CO2 and CH4 adsorption on different rank coals: A thermodynamics study of surface potential, Gibbs free energy change and entropy loss. Fuel 2021, 283, 118886 10.1016/j.fuel.2020.118886. [DOI] [Google Scholar]
- Wang C.; Liu R.; Jiang Y.; Wang G.; Luan H.. Effect of shear-induced contact area and aperture variations on nonlinear flow behaviors in fractal rock fractures J. Rock. Mech. Geotech. 2022, 10.1016/j.jrmge.2022.04.014. [DOI]
- Liu J.; Chen Z.; Elsworth D.; Qu H.; Chen D. Interactions of multiple processes during CBM extraction: a critical review. Int. J. Coal. Geol. 2011, 87, 175–189. 10.1016/j.coal.2011.06.004. [DOI] [Google Scholar]
- Ma T.; Rutqvist J.; Oldenburg C. M.; Liu W. Coupled thermal–hydrological–mechanical modeling of CO2-enhanced coalbed methane recovery. Int. J. Coal. Geol. 2017, 179, 81–91. 10.1016/j.coal.2017.05.013. [DOI] [Google Scholar]
- Chen Z.; Liu J.; Pan Z.; Connell L. D.; Elsworth D. Influence of the effective stress coefficient and sorption-induced strain on the evolution of coal permeability: model development and analysis. Int. J. Greenhouse Gas Control 2012, 8, 101–110. 10.1016/j.ijggc.2012.01.015. [DOI] [Google Scholar]
- Liu T.; Lin B.; Yang W.; Zhai C.; Liu T. Coal permeability evolution and gas migration under non-equilibrium state. Transp. Porous Media 2017, 118, 393–416. 10.1007/s11242-017-0862-8. [DOI] [Google Scholar]
- Peng Y.; Liu J.; Wei M.; Pan Z.; Connell L. D. Why coal permeability changes under free swellings: New insights. Int. J. Coal. Geol. 2014, 133, 35–46. 10.1016/j.coal.2014.08.011. [DOI] [Google Scholar]
- Wang G.; Wang K.; Wang S.; Elsworth D.; Jiang Y. An improved permeability evolution model and its application in fractured sorbing media. J. Nat. Gas. Sci. Eng. 2018, 56, 222–232. 10.1016/j.jngse.2018.05.038. [DOI] [Google Scholar]
- Somerton W. H.; Söylemezog̅lu I. M.; Dudley R. C. Effect of stress on permeability of coal. Int. J. Rock Mech. Min. Sci. 1975, 12, 129–145. 10.1016/0148-9062(75)91244-9. [DOI] [Google Scholar]
- Cui X.; Bustin R. M. Volumetric strain associated with methane desorption and its impact on coalbed gas production from deep coal seams. AAPG Bull. 2005, 89, 1181–1202. 10.1306/05110504114. [DOI] [Google Scholar]
- Wei M. Y.; Liu J.; Liu Y. K.; Liu Z. H.; Elsworth D. Effect of adsorption-induced matrix swelling on coal permeability evolution of micro-fracture with the real geometry. Petrol Sci. 2021, 18, 1143–1152. 10.1016/j.petsci.2021.07.006. [DOI] [Google Scholar]
- Kou Z.; Zhang D.; Chen Z.; Xie Y. Quantitatively determine CO2 geosequestration capacity in depleted shale reservoir: A model considering viscous flow, diffusion, and adsorption. Fuel 2022, 309, 122191 10.1016/j.fuel.2021.122191. [DOI] [Google Scholar]
- Klinkenberg L. J.The Permeability of Porous Media to Liquids and Gases. In Drilling and Production Practice, American Petroleum Institute: Washington, DC, 1941; pp 200–213. [Google Scholar]
- Civan F.; Rai C. S.; Sondergeld C. H. Shale-gas permeability and diffusivity inferred by improved formulation of relevant retention and transport mechanisms. Transp. Porous Media 2011, 86, 925–944. 10.1007/s11242-010-9665-x. [DOI] [Google Scholar]
- Ashrafi Moghadam A.; Chalaturnyk R. Expansion of the Klinkenberg’s slippage equation to low permeability porous media. Int. J. Coal. Geol 2014, 123, 2–9. 10.1016/j.coal.2013.10.008. [DOI] [Google Scholar]
- Wang Z.; Fink R.; Wang Y.; Amann-Hildenbrand A.; Krooss B. M.; Wang M. Gas permeability calculation of tight rocks based on laboratory measurements with non-ideal gas slippage and poroelastic effects considered. Int. J. Rock. Mech. Min. 2018, 112, 16–24. 10.1016/j.ijrmms.2018.10.002. [DOI] [Google Scholar]
- Xiao W.; Bernabé Y.; Evans B.; Mok U.; Zhao J.; Ren X.; Chen M. Klinkenberg effect and effective pressure for gas permeability of tight sandstones. J. Geophys. Res.: Solid Earth 2019, 124, 1412–1429. 10.1029/2018JB016686. [DOI] [Google Scholar]
- Chen Y.; Jiang C.; Leung J. Y.; Wojtanowicz A. K.; Zhang D.; Zhong C. Second-order correction of Klinkenberg equation and its experimental verification on gas shale with respect to anisotropic stress. J. Nat. Gas. Sci. Eng. 2021, 89, 103880 10.1016/j.jngse.2021.103880. [DOI] [Google Scholar]
- Zhou L.; Feng Q.; Chen Z.; Liu J. Modeling and upscaling of binary gas coal interactions in CO2 enhanced coalbed methane recovery. Procedia. Environ. Sci. 2012, 12, 926–939. 10.1016/j.proenv.2012.01.368. [DOI] [Google Scholar]
- Fang H.; Sang S.; Liu S. The coupling mechanism of the thermal-hydraulic-mechanical fields in CH4-bearing coal and its application in the CO2-enhanced coalbed methane recovery. J. Petrol. Sci. Eng. 2019, 181, 106177 10.1016/j.petrol.2019.06.041. [DOI] [Google Scholar]
- Liu J.; Wang J.; Chen Z.; Wang S.; Elsworth D.; Jiang Y. Impact of transition from local swelling to macro swelling on the evolution of coal permeability. Int. J. Coal. Geol. 2011, 88, 31–40. 10.1016/j.coal.2011.07.008. [DOI] [Google Scholar]
- Peng Y.; Liu J.; Pan Z.; Connell L. D.; Chen Z.; Qu H. Impact of coal matrix strains on the evolution of permeability. Fuel 2017, 189, 270–283. 10.1016/j.fuel.2016.10.086. [DOI] [Google Scholar]
- Wei M.; Liu J.; Elsworth D.; Li S.; Zhou F. Influence of gas adsorption induced non-uniform deformation on the evolution of coal permeability. Int. J. Rock. Mech. Min. 2019, 114, 71–78. 10.1016/j.ijrmms.2018.12.021. [DOI] [Google Scholar]
- Zeng J.; Liu J.; Li W.; Guo J. A process-based coal swelling model: Bridging the gaps between localized swelling and bulk swelling. Fuel 2021, 293, 120360 10.1016/j.fuel.2021.120360. [DOI] [Google Scholar]
- Zhang S.; Liu J.; Wei M.; Elsworth D. Coal permeability maps under the influence of multiple coupled processes. Int. J. Coal. Geol. 2018, 187, 71–82. 10.1016/j.coal.2018.01.005. [DOI] [Google Scholar]
- Langmuir I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. 10.1021/ja02242a004. [DOI] [Google Scholar]
- Ren T.; Wang G.; Cheng Y.; Qi Q. Model development and simulation study of the feasibility of enhancing gas drainage efficiency through nitrogen injection. Fuel 2017, 194, 406–422. 10.1016/j.fuel.2017.01.029. [DOI] [Google Scholar]
- Liu H. H.; Rutqvist J. A new coal-permeability model: internal swelling stress and fracture–matrix interaction. Transp. Porous Media 2010, 82, 157–171. 10.1007/s11242-009-9442-x. [DOI] [Google Scholar]
- Mian C.; Zhida C. Effective stress laws for multi-porosity media. Appl. Math. Mech. 1999, 20, 1207–1213. 10.1007/BF02463788. [DOI] [Google Scholar]
- Chen Z.; Liu J.; Elsworth D.; Connell L. D.; Pan Z. Impact of CO2 injection and differential deformation on CO2 injectivity under in-situ stress conditions. Int. J. Coal. Geol. 2010, 81, 97–108. 10.1016/j.coal.2009.11.009. [DOI] [Google Scholar]
- Wu Y.; Liu J.; Elsworth D.; Miao X.; Mao X. Development of anisotropic permeability during coalbed methane production. J. Nat. Gas. Sci. Eng. 2010, 2, 197–210. 10.1016/j.jngse.2010.06.002. [DOI] [Google Scholar]
- Wang L.; Wang Z.; Li K.; Chen H. Comparison of enhanced coalbed methane recovery by pure N2 and CO2 injection: Experimental observations and numerical simulation. J. Nat. Gas. Sci. Eng. 2015, 23, 363–372. 10.1016/j.jngse.2015.02.002. [DOI] [Google Scholar]
- Wang G.; Wang K.; Jiang Y.; Wang S. Reservoir permeability evolution during the process of CO2-enhanced coalbed methane recovery. Energies 2018, 11, 2996. 10.3390/en11112996. [DOI] [Google Scholar]
- Xia T.; Zhou F.; Liu J.; Hu S.; Liu Y. A fully coupled coal deformation and compositional flow model for the control of the pre-mining coal seam gas extraction. Int. J. Rock. Mech. and Min. 2014, 72, 138–148. 10.1016/j.ijrmms.2014.08.012. [DOI] [Google Scholar]
- Vishal V.; Singh T. N.; Ranjith P. G. Influence of sorption time in CO2-ECBM process in Indian coals using coupled numerical simulation. Fuel 2015, 139, 51–58. 10.1016/j.fuel.2014.08.009. [DOI] [Google Scholar]
- Xu H.; Tang D. Z.; Tang S. H.; Zhao J. L.; Meng Y. J.; Tao S. A dynamic prediction model for gas–water effective permeability based on coalbed methane production data. Int. J. Coal. Geol. 2014, 121, 44–52. 10.1016/j.coal.2013.11.008. [DOI] [Google Scholar]
- Leverett M. Capillary behavior in porous solids. Trans. AIME 1941, 142, 152–169. 10.2118/941152-G. [DOI] [Google Scholar]
- Wong S.; Law D.; Deng X.; Robinson J.; Kadatz B.; Gunter W. D.; Zhiqiang F.; et al. Enhanced coalbed methane and CO2 storage in anthracitic coals-Micro-pilot test at South Qinshui, Shanxi, China. Int. J. Greenhouse Gas Control 2007, 1, 215–222. 10.1016/S1750-5836(06)00005-3. [DOI] [Google Scholar]
- Chen D.; Pan Z.; Liu J.; Connell L. D. An improved relative permeability model for coal reservoirs. Int. J. Coal. Geol. 2013, 109–110, 45–57. 10.1016/j.coal.2013.02.002. [DOI] [Google Scholar]













