Hierarchical Multi-Geodesic Model for Longitudinal Analysis of Temporal Trajectories of Anatomical Shape and Covariates

Abstract

Longitudinal regression analysis for clinical imaging studies is essential to investigate unknown relationships between subject-wise changes over time and subject-specific characteristics, represented by covariates such as disease severity or a level of genetic risk. Image-derived data in medical image analysis, e.g. diffusion tensors or geometric shapes, are often represented on nonlinear Riemannian manifolds. Hierarchical geodesic models were suggested to characterize subject-specific changes of nonlinear data on Riemannian manifolds as extensions of a linear mixed effects model. We propose a new hierarchical multi-geodesic model to enable analysis of the relationship between subject-wise anatomical shape changes on a Riemannian manifold and multiple subject-specific characteristics. Each individual subject-wise shape change is represented by a univariate geodesic model. The effects of subject-specific covariates on the estimated subject-wise trajectories are then modeled by multivariate intercept and slope models which together form a multi-geodesic model. Validation was performed with a synthetic example on a S² manifold. The proposed method was applied to a longitudinal set of 72 corpus callosum shapes from 24 autism spectrum disorder subjects to study the relationship between anatomical shape changes and the autism severity score, resulting in statistics for the population but also for each subject. To our knowledge, this is the first longitudinal framework to model anatomical developments over time as functions of both continuous and categorical covariates on a nonlinear shape space.

1. Introduction

Recent advances in medical image analysis allow researchers to track an individual subject’s development with multiple repeated observations [4]. Longitudinal regression analysis, which adequately accounts for intra-subject correlation, is essential to estimate unknown relationships between subject-specific temporal changes and characteristics of individuals via repeated observations [2].

Data derived from medical images, such as diffusion tensors, diffeomorphic deformations, or geometric shapes, are to be analyzed on their natural nonlinear spaces, e.g. Riemannian manifolds. For longitudinal analysis of nonlinear data on a Riemannian manifold, hierarchical geodesic models were suggested as extensions of a linear mixed effects model on Euclidean space [6, 7, 9]. These methods estimate the same model for both subject and population levels which is a direct reformulation of a linear mixed effects model on a Riemannian manifold. The previous methods face challenges from too few observations per subject to hierarchically solve a multivariate model at a subject level even though the number of subjects may be sufficient. Despite the importance of including subject-specific characteristics for longitudinal analysis, a hierarchical model that analyzes the relationship between subject-wise morphological changes over time and multiple covariates on a Riemannian manifold has not been shown before.

We propose a novel hierarchical multi-geodesic model for longitudinal analysis of subject-specific morphological changes of anatomical structures on a Riemannian manifold. Each subject-wise morphological change over time is modeled by a univariate geodesic model which only requires a minimum of two observations per subject. The effects of subject-specific characteristics, represented by subject-specific covariates, on subject-wise trajectories are modeled by a multi-geodesic model. The covariates are fixed for an individual subject but varying across a population. The multi-geodesic model consists of multivariate intercept and slope models which account for the effects of the subject-specific characteristics to subject-wise baselines and developments over time, respectively. It is worth noting that the proposed method is different from the direct extension of a linear mixed effects model because the relationship between subject-specific characteristics and the slopes of subject-wise temporal trajectories cannot be modeled by linearly adding the covariates as additional explanatory variables.

A synthetic example on a S² manifold with a comparison to the ground truth showed the feasibility of the proposed method. Experimental validation on 72 corpus callosum shapes represented on a nonlinear shape space from 24 autism spectrum disorder subjects with different autism severity scores demonstrate the capability of the proposed method for longitudinal analysis of the relationship between subject-specific morphological changes and multiple covariates.

2. Method

Background on Riemannian Geometry:

A geodesic is a zero-acceleration curve on an n-dimensional Riemannian manifold M. It has the minimizing property that there is no curve shorter than a geodesic between any two points within a small neighborhood. An exponential map Exp(p, v) = q is a mapping of p ∈ M to q ∈ M along a geodesic going out from p in the direction and magnitude of v. Its inverse, Log(p, q) = v, is defined onto a neighborhood U(p) of p. The Riemannian distance between p and q is the length of a geodesic between the two, d(p, q) = ∥Log(p, q)∥. Parallel transport ψ_p→q(u) of a tangent vector u ∈ T_pM along a differentiable curve c(t) : I → M from p to q is defined by a unique parallel vector field V (t) along c(t) where I = [0, 1], c(0) = p, and c(1) = q. V (t) satisfies V (t₀) = u and $\frac{DV}{dt}=0$, where $\frac{DV}{dt}$ is a covariant derivative of a vector field V. Parallel transport has the following angle and scale preserving properties: the angle of u along c(t) does not change, $\frac{DV}{dt}=0$, and the scale of u also does not change, ∥u∥ = ∥V (t)∥, at any t ∈ I [1]. ψ_p→q(u) is not unique and depends on a curve c that connects p and q. We will only use ψ_p→q along with the unique geodesic between p and q to guarantee the transport to be unique.

Subject-wise Trajectory Estimation:

Let y_ij ∈ M be the jth observation of the ith subject associated with time $t_{ij}\in ℝ$, i = 1,…, N_s,$j=1,\dots ,N_{obs}^i$. N_s and $N_{obs}^i$ are the number of subjects and the number of observations of the ith subject, respectively. We estimate a subject-wise trajectory Y_i by the least squares geodesic regression model [3].

$$({\widehat{a}}_i,{\widehat{b}}_i)=\underset{a_i,b_i}{\mathrm{argmin}}\sum _{j=1}^{N_{obs}^i}{d}^2\left(y_{ij},Exp\left(a_i,b_i{t}_{ij}\right)\right),Y_i=Exp({\widehat{a}}_i,{\widehat{b}}_{i}t),$$ (1)

where a_i ∈ M and b_i ∈ T_aiM are an intercept and a slope tangent vector of the geodesic model Y_i for the ith subject’s trajectory as shown in Fig. 1 (a). It is worth noting that Eq. 1 only requires the minimum of two observations per subject to solve for two coefficients, an intercept a_i and a slope b_i.

Fig. 1:

Illustration of the proposed method. (a) Subject-wise geodesic trajectory estimation. (b) The example of an intercept model f(c) with a single covariate c. (c) Stop-over parallel transport ϕ from ${\widehat{a}}_2$ to ${\widehat{\beta }}_0$.

Hierarchical Multi-Geodesic Model:

Let the ith subject be associated with two sets of subject-specific covariates for intercepts ${\mathit{\eta }}^i=\{{\eta }_1^i,\dots ,{\eta }_{N_{\eta }}^i\}$ and slopes ${\mathit{\theta }}^i=\{{\theta }_1^i,\dots ,{\theta }_{N_{\theta }}^i\}$, where N_η and N_θ are the numbers of the covariates.

We aim to model the effects of η and θ on subject-wise trajectories. The proposed Hierarchical Multi-Geodesic model (HMG) consists of an intercept model f(η) and a slope model g(θ),

$$Y=Exp(Exp(f(\mathit{\eta }),g(\mathit{\theta })t),ϵ).$$ (2)

Intercept Model:

The intercept model f(η) is formulated as a multivariate geodesic model with a base intercept β₀ ∈ M and tangent vectors ${\beta }_k\in T_{{\beta }_0}M$ [5],

$$f(\mathit{\eta })=Exp\left({\beta }_0,{\beta }_1{\eta }_1+\dots +{\beta }_{N_{\eta }}{\eta }_{N_{\eta }}\right).$$ (3)

β_k, k = 1, …, N_η, are coefficients that represent the effects of subject-specific covariates η_k to the intercepts of subject-wise trajectories. For example, a hypothesis that a subject diagnosed with autism and a healthy subject might have different baseline corpus callosum shapes at 3-month after birth can be modeled by the intercept model f. The coefficients β_k can be estimated by a least squares formulation of the multivariate geodesic model,

$$({\widehat{\beta }}_0,{\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_{N_{\eta }})=\underset{{\beta }_0,\dots ,{\beta }_{N_{\eta }}}{\mathrm{argmin}}\sum _{i=1}^{N_s}{d}^2\left(f\left({\mathit{\eta }}^i\right),{\widehat{a}}_i\right).$$ (4)

We optimize Eq. 4 by a Euclideanized optimization scheme similar to [5] with an iterative update of an anchor point to the estimated intercept, instead of fixing it at the intrinsic mean of given data. The estimated intercept model is given as $\widehat{f}(\mathit{\eta })=Exp({\widehat{\beta }}_0,{\widehat{\beta }}_1{\eta }_1+\dots +{\widehat{\beta }}_{N_{\eta }}{\eta }_{N_{\eta }})$ after optimization.

The least squares formulation Eq. 4 assumes that the distribution of subject-wise intercepts around $\widehat{f}(\mathit{\eta })$ is the generalized normal distribution [3],

$${\widehat{a}}_i=\mathrm{Exp}(\widehat{f}\left({\mathit{\eta }}^i\right),{ϵ}_a)$$ (5)

where ${ϵ}_a~N\left(0,{\sigma }_a^2\right)\cdot {ϵ}_a$ can be directly interpreted as random effects of subject-wise intercepts that indicate longitudinal effects of repeated observations of individual subjects [2]. Fig. 1 (b) shows the illustration of the concept of the intercept model f with an example model with one continuous covariate c.

Tangent Vector Space of Slope Model:

The effects of covariates on the slopes of subject-wise trajectories are modeled as a linear model g₀(θ) on a tangent vector space from a set of subject-wise slope tangent vectors ${\widehat{b}}_i$,

$$g_0(\mathit{\theta })={\gamma }_0+{\gamma }_1{\theta }_1+\dots +{\gamma }_{N_{\theta }}{\theta }_{N_{\theta }},$$ (6)

where γ_k, k = 0, …, N_θ, are coefficient tangent vectors associated with θ_k. The model can explain a hypothesis on the relationship between covariates and the slopes. For example, a corpus callosum may develop differently from a baseline for a subject diagnosed with autism versus a healthy subject.

There are two problems that we need to consider to model subject-wise slopes. First, γ_k must be on a single tangent vector space to be linearly combined as in Eq. 6. For consistent modeling and comprehensible interpretation, we set γ_k to be on a tangent vector space of the base intercept of the intercept model, $T_{{\widehat{\beta }}_0}M$, which makes $g_0(\mathit{\theta })\in T_{{\widehat{\beta }}_0}M$. Second, ${\widehat{b}}_i$ are not directly comparable to each other because they are on different tangent vector spaces $T_{{\widehat{a}}_i}M$. Therefore, we need to properly transport ${\widehat{b}}_i$ to $T_{{\widehat{\beta }}_0}M$ to estimate γ_k.

Stop-Over Parallel Transport ϕ:

Recall that subject-wise intercepts ${\widehat{a}}_i$ are the combination of the fixed effects intercept model $\widehat{f}\left({\mathit{\eta }}^i\right)$ and the random effects ϵ_a on subject-wise intercepts as explained in Eq. 5. In other words, each ${\widehat{a}}_i$ is randomly distributed in the normal distribution of the random effects centered at $\widehat{f}\left({\mathit{\eta }}^i\right)$ [8]. Therefore, we need to transport a tangent vector on $T_{{\widehat{a}}_i}M$ to $T_{\widehat{f}\left({\mathit{\eta }}^i\right)}M$ first to account for the random effects and then from $T_{\widehat{f}\left({\mathit{\eta }}^i\right)}M$ to $T_{{\widehat{\beta }}_0}M$ to account for the fixed effects as shown in Fig. 1 (c) by a stop-over parallel transport ϕ,

$${\tilde{b}}_i=\varphi ({\widehat{b}}_i)={\psi }_{\widehat{f}({\mathit{\eta }}^i)\to {\widehat{\beta }}_0}({\psi }_{{\widehat{a}}_i\to \widehat{f}({\mathit{\eta }}^i)}({\widehat{b}}_i)),$$ (7)

where ${\tilde{b}}_i\in T_{{\widehat{\beta }}_0}M$. ψ is a parallel transport along with a geodesic between two points with the angle and scale preserving properties that suit our need to consistently transport ${\widehat{b}}_i$ at each stage of the stop-over transport. Fig. A1 in the appendix shows the effect of the stop-over parallel transport with a synthetic experiment on a S² manifold. The direct parallel transportation to the intercept point may arbitrarily rotate tangent vectors when the stop-over transport preserves the directions of the tangent vectors consistently.

Slope Model Estimation:

With ${\widehat{b}}_i$ transported to $T_{{\widehat{\beta }}_0}M$ by ϕ, we estimate slope coefficients γ_k, k = 0, …, N_θ, in g₀(θ). It can be formulated as the least squares formulation of a standard multivariate linear regression problem [2],

$$\left({\widehat{\gamma }}_0,{\widehat{\gamma }}_1,\dots ,{\widehat{\gamma }}_{N_{\theta }}\right)=\underset{{\gamma }_0,{\gamma }_1,\dots ,{\gamma }_{N_{\theta }}}{\mathrm{argmin}}\sum _{i=1}^{N_s}{\Vert {\gamma }_0+{\gamma }_1{\theta }_1^i+\dots +{\gamma }_{N_{\theta }}{\theta }_{N_{\theta }}^i-{\tilde{b}}_i\Vert }^2.$$ (8)

Eq. 8 is optimized by the closed-form solution of a multivariate linear regression problem with the assumption of no correlation in γ_k. The estimated slope model ${\widehat{g}}_0(\mathit{\theta })={\widehat{\gamma }}_0+{\widehat{\gamma }}_1{\theta }_1+\dots +{\widehat{\gamma }}_{N_{\theta }}{\theta }_{N_{\theta }}$ is transported to the respective tangent vector space of the intercept model $\widehat{f}(\mathit{\eta })$,$\widehat{g}(\mathit{\theta })={\psi }_{{\widehat{\beta }}_0\to \widehat{f}(\mathit{\eta })}\left({\widehat{g}}_0(\mathit{\theta })\right)$.

The least squares formulation in Eq. 8 is related to the random effects of subject-wise slopes, similar to Eq. 5 for the intercept model. The complete estimated multi-geodesic model is then formulated as $y=\mathrm{Exp}(\widehat{f}(\mathit{\eta }),\widehat{g}(\mathit{\theta })t)$.

3. Experiments

Synthetic Example on S² Manifold:

We tested our method with a synthetic example on a S² manifold. We used the exponential map, log map, and parallel transport of S² manifold as in [7]. 3527 points of 1000 subjects were generated by the following model with time t ∈ (20, 70) and a continuous covariate c ∈ (0, 5),

$$y=Exp(Exp(f(c),g(c)t)),f(c)=Exp\left({\beta }_0,{\beta }_{1}c\right),g(c)={\psi }_{{\beta }_0\to f(c)}\left({\gamma }_0+{\gamma }_{1}c\right),$$

where we assigned β₀ = [1, 0, 0], β₁ = [0, 0, 0.4], γ₀ = [0, 0.01, 0.02], and γ₁ = [0, 0.002, −0.003] with random effects on intercepts ϵ_a ~ N(0, 0.05²) and slopes ϵ_b ~ N(0, 0.001²) and the data observation noise ϵ ~ N(0, 0.001²).

Fig. 2(a) shows the synthetic data colored by c from blue to green. The estimated subject level geodesic models are plotted as translucent white curves. Fig. 2(b) shows the estimated geodesic of a geodesic regression model (SG, magenta) with data points colored by t from black to white [3]. Fig. 2(c) illustrates the results of a Hierarchical Single Geodesic model (HSG, brown) [5, 7]. The results of the proposed Hierarchical Multi-Geodesic model (HMG) and the ground truth (yellow curves) are displayed in Fig. 2(d) with uniformly selected values of c with a unit interval from 0.5 to 4.5. The generalized R² with respect to individual data of SG, HSG, and the proposed HMG were 0.31, 0.29, and 0.96, respectively [3]. The R² with respect to subject-wise intercepts $R_a^2$ and slopes $R_b^2$ of the proposed HMG were 0.98 and 0.90. $R_a^2$ and $R_b^2$ of HSG are zero since the HSG is the average trajectory of the subject-wise trajectories [7]. Validation with respect to subject-wise trajectories is not available for non-longitudinal SG. Standard deviations of the random effects estimated by HMG of subject-wise intercepts and slopes are σ_a = 0.09 and σ_b = 0.002, respectively.

Fig. 2:

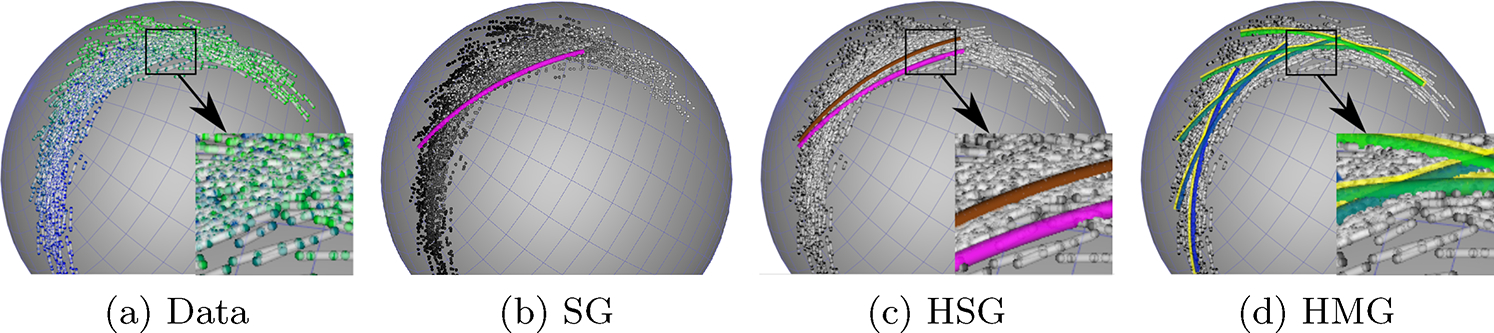
Synthetic Example on a S² manifold. (a) Generated data points colored by associated values of a covariate c (blue to green) with subject-wise trajectories (white lines). (b) Estimated single geodesic model (SG, magenta). Data points are colored by time (black to white). (c) Estimated hierarchical single geodesic model (HSG, brown). (d) Estimated hierarchical multi-geodesic model (HMG) and the ground truth (yellow) visualized with selected values of c.

Longitudinal Corpus Callosum Shape Changes:

Previous research demonstrated differences of corpus callosum (CC) size in autism [10], stating that it is thicker in infants later diagnosed with autism by multi-level linear analysis of derived features from shapes, such as mean thickness. Applying the proposed framework, quantitative exploration of longitudinal shape changes as a function of diagnostic scores becomes possible, resulting in population level and subject-specific models. We modeled HMG with sex s and Autistic Diagnostic Observation Schedule (ADOS) severity score AS, which combines symptoms related to a social interaction and a repetitive behavior with scores ranging from 4 to 10 for autism spectrum disorder (ASD) subjects. Larger AS indicate higher severity of autism. Seventy-two CC shapes from 24 ASD subjects (9 females and 15 males) from the ACE-IBIS study were used for the experiment [10]. Each subject was repeatedly scanned three times. Because the development of CC is known to be asymptotic to a logarithm [10], we reparametrized time t by taking the natural log to model the asymptotic shape changes over time.

$$y=Exp(Exp(f(s,AS),g(s,AS)\log (t))),$$

$$f(s,AS)=Exp\left({\beta }_0,{\beta }_{1}s+{\beta }_{2}AS\right),g(s,AS)={\psi }_{{\beta }_0\to f(s,AS)}\left({\gamma }_0+{\gamma }_{1}s+{\gamma }_{2}AS\right),$$

with sex s, 0 for male and 1 for female, age(month) t = (6, 25), and AS = (4, 10).

CC shapes were represented on a product manifold $\mathbf{M}=ℝ\times ℂP^{k-2}$ of a scale $\rho \in ℝ$, which represents a shape size, and a Kendall shape z with k points in 2D Kendall shape space $ℂP^{k-2}$, where translation, rotation, and scale of shapes are removed. The squared distance between p = (ρ_p, z_p) and q = (ρ_q, z_q) on M is a weighted sum of the distances on the element spaces. The distance on $ℂP^{k-2}$ is normalized by the ratio of variances of data distributions of scales ρ and Kendall shapes z, $d^2(p,q)={\Vert log\left({\rho }_p,{\rho }_q\right)\Vert }^2+\frac{{\sigma }_{\rho }^2}{{\sigma }_{\mathbf{z}}^2}{\Vert log\left({\mathbf{z}}_p,{\mathbf{z}}_q\right)\Vert }^2$, where ${\sigma }_{\rho }^2$ and ${\sigma }_{\mathbf{z}}^2$ are the variances of the input data of scales ρ and shapes z, respectively [8]. One hundred landmark points were sampled at corresponding locations from each shape boundary. We used the exponential map, log map, and parallel transport of $ℂP^{k-2}$ as in [3]. The exponential and log maps of $ℝ$ are addition and subtraction, respectively. The parallel transport of $ℝ$ is an identity function.

Fig. 3 displays the estimated longitudinal trends with fixed s=0 of 15 male subjects. Fig. 3 (a) shows the estimated longitudinal shape trends of the lowest and the highest ADOS scores over time. The difference of the shape changes is more evident in Fig. 3(b) illustrating estimated baseline and end point shapes with varying ADOS scores at 3 and 24-month of age. One can observe the increased expansion of the anterior CC (the genu and rostral body) for subjects with higher ADOS scores which confirms previous clinical finding that subjects diagnosed with autism tend to have larger corpus callosum [10]. The population level longitudinal trends of shape sizes estimated from the subject-wise trends in Fig. 3(c) quantitatively show increasing trends of shape sizes with higher ADOS scores in Fig. 3(d). The overall R² values of SG, HSG, and HMG were 0.23, 0.23, and 0.27, respectively. The root mean squared error measured by average surface boundary landmark distances of SG, HSG, and HMG were 0.287, 0.287, and 0.277 (mm), respectively. Table 1 summarizes the quantitative evaluations. Mean and standard deviation of R² values of the subject-wise trends were 0.89±0.04.

Fig. 3:

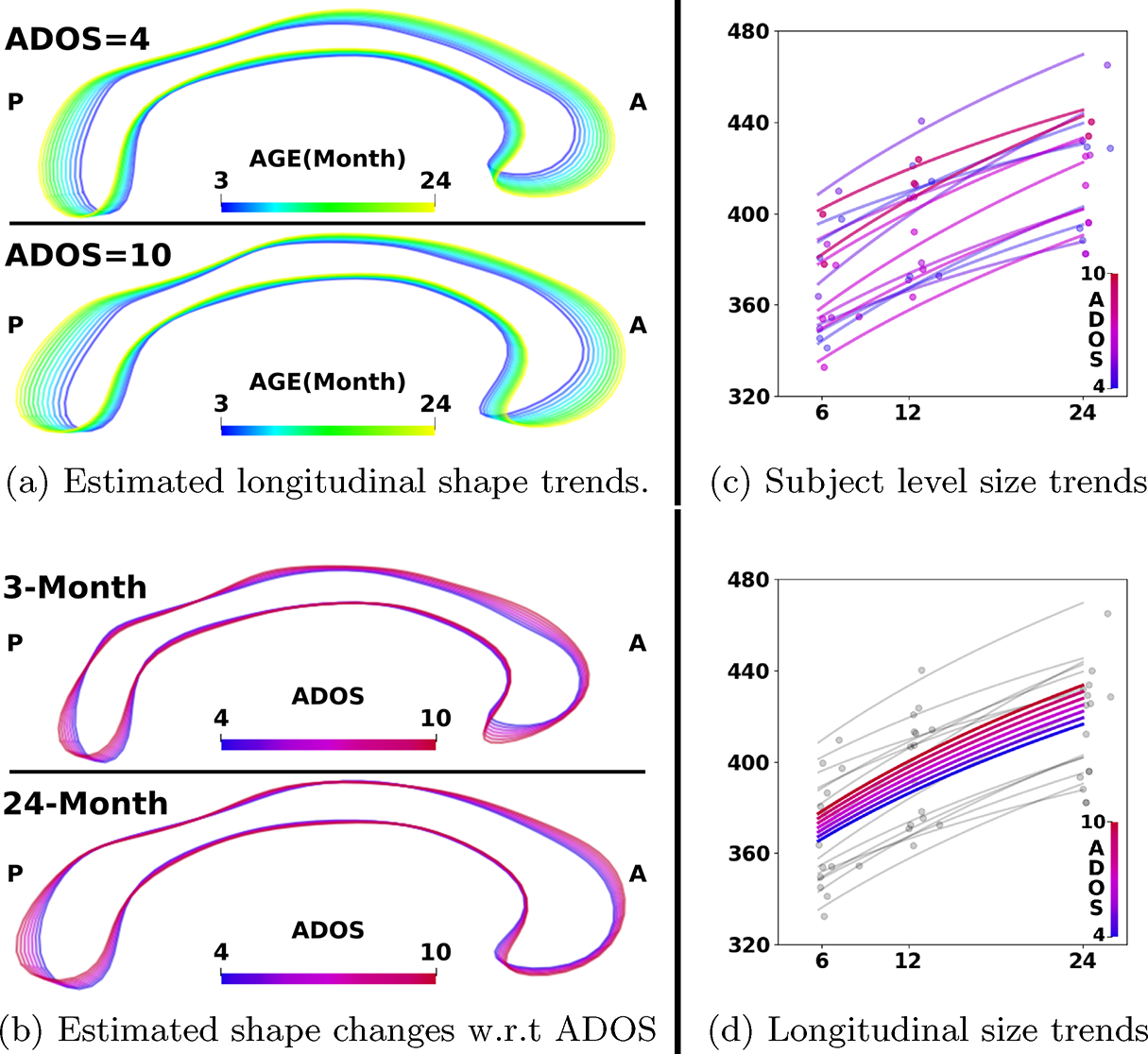
Estimated longitudinal corpus callosum (CC) shape changes of 15 male subjects (A:Anterior, P:Posterior). (a) Population level longitudinal shape trends of subjects with the lowest and the highest ADOS scores. (b) Shape changes with varying ADOS scores of baseline shapes at 3-month and end point shapes at 24-month. (c) The observed shape sizes with estimated subject-level trends. (d) Population level longitudinal size trends with varying ADOS scores.

Table 1:

Quantitative comparisons of SG, HSG, and the proposed HMG. R² with respect to observations(R²), subject-wise intercepts($R_a^2$) and slopes($R_b^2$), the standard deviations of subject-wise intercepts(σ_a) and slopes(σ_b), and the root mean squared boundary landmark distances(RMSE) are listed.

	Synthetic					CC-Autism Spectrum
	R 2	$R_a^2$	$R_b^2$	σa	σb	R 2	$R_a^2$	$R_b^2$	σa	σa	RMSE(mm)
SG	0.31	N/A	N/A	N/A	N/A	0.23	N/A	N/A	N/A	N/A	0.287
HSG	0.29	0.0	0.0	0.58	5.0e−3	0.23	0.0	0.0	1.02e−a	5.15e−3	0.287
HMG	0.96	0.98	0.90	0.09	2.0e −3	0.27	0.06	0.09	9.55e −3	4.68e −3	0.277

4. Discussion

The proposed hierarchical multi-geodesic model is a novel method for longitudinal analysis of subject-specific anatomical shape changes on a Riemannian manifold. It enables longitudinal analysis with multiple covariates directly on a nonlinear shape space which has not yet been possible for clinical studies. The application to subject-specific corpus callosum shape changes demonstrated promising results that confirmed clinical finding of the relationship between the anatomical development and diagnostic scores of individual subjects. We will focus on a hypothesis testing framework for the proposed model to further explore relationships between temporal change of anatomical structures and covariates.