Implications of covariate induced test dependence on the diagnostic accuracy of latent class analysis in pulmonary tuberculosis

Highlights

• •Residual dependence induced by a measured covariate remains after performing standard LCA. This violates key assumptions of standard LCA hence incorrect inferences
• •Models accounting for heterogeneity in diagnostic accuracy yield realistic estimates
• •Carefully consider factors known to affect diagnostic test performance e.g. severe comorbidity
• •Covariate-adjusted LCA alleviate bias implied by heterogeneity in diagnostic test accuracy. Therefore, we recommended it.

Abstract

Background

In application studies of latent class analysis (LCA) evaluating imperfect diagnostic tests, residual dependence among the diagnostic tests still remain even after conditioning on the true disease status due to measured variables known to affect prevalence and/or alter diagnostic test accuracy. Presence of severe comorbidities such as HIV in pulmonary tuberculosis (PTB) diagnosis alter the prevalence of PTB and affect the diagnostic performance of the available imperfect tests in use. This violates two key assumptions of LCA: (1) that the diagnostic tests are independent conditional on the true disease status (2) that the sensitivity and specificity remain constant across subpopulations. This leads to incorrect inferences.

Methods

Through simulation we examined implications of likely model violations on estimation of prevalence, sensitivity and specificity among passive case-finding presumptive PTB patients with or without HIV. Jointly conditioning on PTB and HIV, we generated independent results for five diagnostic tests and analyzed using Bayesian LCA with Probit regression, separately for sets of five and three diagnostic tests using four working models allowing: (1) constant PTB prevalence and diagnostic accuracy (2) varying PTB prevalence but constant diagnostic accuracy (3) constant PTB prevalence but varying diagnostic accuracy (4) varying PTB prevalence and diagnostic accuracy across HIV subpopulations. Vague Gaussian priors with mean 1 and unknown variance were assigned to the model parameters with unknown variance assigned Inverse Gamma prior.

Results

Models accounting for heterogeneity in diagnostic accuracy produced consistent estimates while the model ignoring it produces biased estimates. The model ignoring heterogeneity in PTB prevalence only is less problematic. With five diagnostic tests, the model assuming homogenous population is robust to violation of the assumptions.

Conclusion

Well-chosen covariate-specific adaptations of the model can avoid bias implied by recognized heterogeneity in PTB patient populations generating otherwise dependent test results in LCA.

1. Introduction

Lack of a perfect reference standard complicates evaluation of new diagnostic tests and quantification of disease prevalence. Ideally, new diagnostic tests are evaluated by comparison to a gold standard (GS) test that conclusively determines the diagnosis. However, in practice, the GS test is rarely available. As a result, new diagnostic tests are assessed by comparison to available imperfect reference tests. Due to the inherent limitation of imperfect reference tests, discrepant resolution and composite reference standard methods were proposed to alleviate imperfect reference standard bias [1]. Both methods, however, yield biased estimates [2], [3], [4]. Another promising approach is the use of latent class analysis (LCA) [5], [6], [7]. This approach is used for identifying unobserved subgroups in the population [8]. It has enjoyed extensive application in many disciplines [9]. Over the past few decades, it has attracted attention in biomedical field, including evaluation of diagnostic tests in the absence of a gold standard in the field of infectious disease [9], [10].

Consider, for example, the diagnosis of pulmonary tuberculosis (PTB). The current conventional diagnostic methods for PTB involve culture, smear microscopy, Xpert MTB/RIF, Xpert MTB/RIF Ultra, and imaging (chest X-ray, Computed Tomography) in a patient with presumptive TB. Recently, Computer-Aided Detection for TB (CAD4TB) and C-reactive protein (CRP) were proposed as triage tests in presumptive TB patients before ordering an expensive but more accurate Xpert MTB/RIF [11]. Lateral Flow test for lipoarabinomannan (LAM) in urine is recommended for diagnosis of TB in patients with advanced HIV disease [12], [13], [14]. The conventional reference standard for diagnosis of PTB is culture for Mycobacterium tuberculosis complex. While culture is the most specific test available, an imperfect sensitivity (76%–92%) is a limitation [15]. Thus, a negative culture test result does not rule out the presence of TB. PTB diagnosis could use as few as two symptoms/tests e.g. ‘cough lasting more than two weeks and chest X-ray’ or ‘any TB symptom and chest X-ray’, to more elaborate combinations of three e.g. ‘any TB symptom, chest X-ray and Xpert MTB/RIF’ or four e.g. adding culture to the set [16]. In this context we consider any TB symptom as a diagnostic test. A combination of tests that does not include TB symptoms in the set has also been considered [17]. Using a combination of imperfect diagnostic tests as the reference standard will potentially lead to biased estimates [18]. Composite reference standard (CRS) does not take into account the underlying uncertainties attributable to each imperfect test while assessing the diagnostic accuracy of the new test. A detailed discussion on the concerns of CRS has been provided elsewhere [4]. Alternatively, with such a set of test results jointly available for a sample of patients, LCA allows not only for improved patient diagnosis but further allows evaluation of the diagnostic tests themselves. It yields correct estimates of disease prevalence and diagnostic test accuracy under nontrivial assumptions [19]. These strong assumptions are violated when a serious comorbidity affects the diagnostic test accuracy and/or risk of the targeted disease. This then results in biased estimates of disease prevalence and diagnostic test accuracy [3], [20], [21], [22]. However, there is scanty evidence on the performance of latent class models in the presence of differential diagnostic test accuracy induced by an observed external covariate that is also associated with the risk of the targeted disease.

Previous authors in their work have adjusted for covariates known to influence diagnostic test accuracy based on expert opinion [22], [23], some did not adjust for covariates [24] while others adjust for the effect of covariates on disease prevalence only [5], [6], [21]. Thus, the differing approaches on how to conduct LCA leaves an important gap in diagnostic test evaluation, especially in TB where factors such as HIV status, history of TB and malnutrition affect the performance of Xpert MTB/RIF, TB symptoms and tuberculin skin test among others [16], [22], [25]. It is unclear whether studies that fail to adjust for measured covariates as well as those that partly adjust for the effects of measured covariates on diagnostic test accuracy only yield biased estimates while those that correctly adjust for the effect of measured covariates have a better chance of obtaining correct inferences. Using simulation, we performed Bayesian LCA separately for a set of three (any PTB symptom, CAD4TB, Xpert MTB/RIF) and a set of five diagnostic tests (any PTB symptom, CRP, CAD4TB, Xpert MTB/RIF and culture) for PTB with the aim of assessing the impact of covariate induced diagnostic test dependence on the performance of latent class models. We evaluated the likelihood of four proposed models, representing common situations under which the standard assumptions are violated for a set of three and a set of five diagnostic tests and offer recommendations for analysis.

2. Simulation conditions: the generated data

We generated data mimicking a setting of passive case-finding among presumptive PTB patients with or without HIV. Our goal is to show the effect of residual dependence induced by a measured covariate on the diagnostic performance of LCA after conditioning on the true PTB status and isolating the dependence between the diagnostic tests attributable to other sources. Based on realistic sensitivities and specificities of five diagnostic tests for PTB (any PTB symptom, CRP, CAD4TB, Xpert MTB/RIF and culture) we simulated independent test results conditional on PTB and HIV (Table A.1 in Appendix A). We thus simulated 20% HIV+ patients with 5% PTB prevalence in HIV− and 10% in HIV+, for an overall prevalence of 6% [26], [27]. The accuracy used for culture was based on a composite reference standard of BACTEC 960/MGIT, BACTEC 460 and solid media [15] For the other diagnostic tests it was based on culture as the reference standard. The overall sensitivity (specificity) averages the test-related sensitivity (specificity) over the HIV subpopulations. Thus, the joint probability of the $j^{\mathit{th}}$ diagnostic test $Y_j,j=1,2,3,\cdots ,J,$ PTB status $D$ and covariate (HIV status) $X$ was generated using the following model.

$$Pr\left(Y_j,D,X\right)=Pr\left(Y_j|D,X\right)Pr\left(D|X\right)Pr\left(X\right)$$

Hence for the set of test results under conditional independence given D and X:

$$Pr\left(Y_1,Y_2,\cdots ,Y_J,D,X\right)=\prod _{j=1}^{J}Pr\left(Y_j|D,X\right)Pr\left(D|X\right)Pr\left(X\right)$$

where $Y_j=1\mathrm{i}\mathrm{f}\mathrm{t}\mathrm{h}\mathrm{e}{j}^{\mathit{th}}\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e},0\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e};D=1\mathrm{i}\mathrm{f}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{P}\mathrm{T}\mathrm{B}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e},0\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e};X=1\mathrm{i}\mathrm{f}\mathrm{H}\mathrm{I}\mathrm{V}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{s}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}(\mathrm{i}.\mathrm{e}\mathrm{H}\mathrm{I}\mathrm{V}+),0\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}$.

We introduced the observed covariate $X$ in the relevant models to handle dependence of diagnostic tests induced by this covariate.

We thus generated three pseudo-random populations of 1000, 2000 and 5000 individuals with their true PTB and HIV status. Each of the three pseudo-random populations were replicated 100 times. The covariance and correlation structures are presented in Appendix A (Table A.2–A.5).

3. Working models

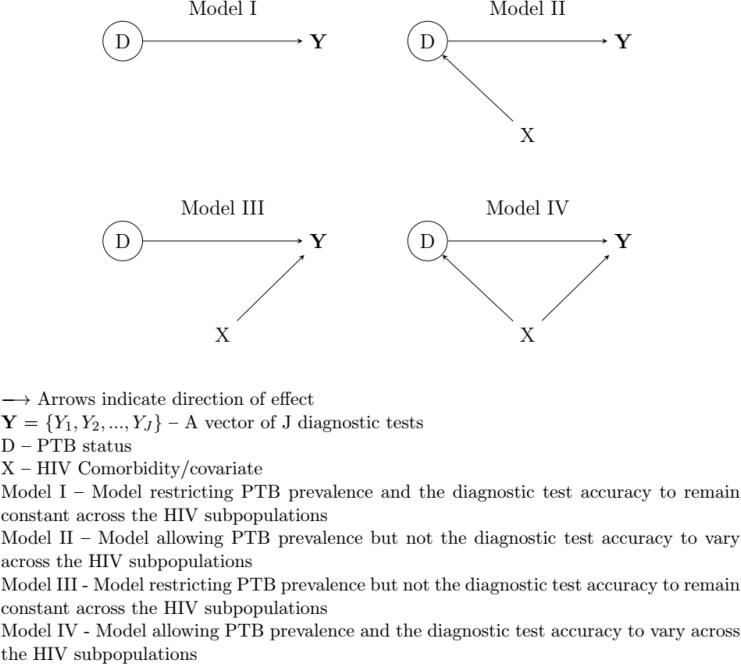
The standard two-class LCA assumes that the study population consists of at least two separate, internally homogenous latent classes. We consider a person’s true PTB status consisting of two mutually exclusive and exhaustive categories: ‘PTB’ and ‘non-PTB’. We acknowledge that this may not be true in practice because PTB status for an individual may be any of (1) active-TB (2) no TB (3) latent/subclinical TB [28]. However, we restrict ourselves to the case where we have two classes: PTB and non-PTB, for the purpose of assessing violation of model assumptions. The model further assumes that the result of one diagnostic test does not depend on the results of other tests (and persons) in the latent class, with a constant chance of error across individuals in a latent class, implying constant test sensitivity and specificity across subpopulations [5]. In practice, these standard latent class model assumptions are violated, especially in the field of TB where, for example, HIV disease is known to influence the performance of some diagnostic tests including TB symptoms and Xpert MTB/RIF. To assess the effect of the measured covariate on the performance of latent class analysis, we analyzed the data using four working models: from most simple – with no HIV dependence – to the accurate (or complex) model representing the true model used to generate the data (Fig. 1). These are variants of the standard two-class latent class model. Their detailed description is given in Appendix A.

Fig. 1.

Graphical presentation of the working models.

The joint probability $Pr\left(Y_{i1}=y_{i1},Y_{i2}=y_{i2},Y_{i3}=y_{i3},\cdots ,Y_{\mathit{iJ}}=y_{\mathit{iJ}}|X_i=x_i\right)=Pr\left(Y_i={\mathit{y}}_{\mathit{i}}|X_i=x_i\right)$ of observing a combination of J test results $y_{i1},y_{i2},y_{i3,}\cdots ,y_{\mathit{iJ}}$ applied to the $i^{\mathit{th}}$ individual,$i=1,2,3,\cdots ,N$, was derived from the assumption of constant (or varying) PTB prevalence and diagnostic test accuracy across the HIV subpopulations as.

Model I: assuming independence of (Y, D) from X

$$Pr\left({\mathit{y}}_{\mathit{i}}\right)=\sum _{d=0}^{d=1}\prod _{j=1}^{J}Pr\left(Y_{\mathit{ij}}=y_{\mathit{ij}}|D_i=d\right)Pr\left(D_i=d\right)$$

Model II: assuming.$Pr\left(Y_{\mathit{ij}}=y_{\mathit{ij}}|D_i=d,X_i=x_i\right)=Pr\left(Y_{\mathit{ij}}=y_{\mathit{ij}}|D_i=d\right)$

$$Pr\left({\mathit{y}}_{\mathit{i}}|X_i=x_i\right)=\sum _{d=0}^{d=1}\prod _{j=1}^{J}Pr\left(Y_{\mathit{ij}}=y_{\mathit{ij}}|D_i=d\right)Pr\left(D_i=d|X_i=x_i\right)$$

Model III: assuming.$Pr\left(D_i=d|X_i=x_i\right)=Pr\left(D_i=d\right)$

$$Pr\left({\mathit{y}}_{\mathit{i}}|X_i=x_i\right)=\sum _{d=0}^{d=1}\prod _{j=1}^{J}Pr\left(Y_{\mathit{ij}}=y_{\mathit{ij}}|D_i=d,X_i=x_i\right)Pr\left(D_i=d\right)$$

Model IV

$$Pr\left({\mathit{y}}_{\mathit{i}}|X_i=x_i\right)=\sum _{d=0}^{d=1}\prod _{j=1}^{J}Pr\left(Y_{\mathit{ij}}=y_{\mathit{ij}}|D_i=d,X_i=x_i\right)Pr\left(D_i=d|X_i=x_i\right)$$

4. Analysis

We implemented Bayesian LCA to evaluate diagnostic test properties of a set of five diagnostic tests: any PTB symptom, CAD4TB, CRP, Culture and Xpert MTB/RIF. A subset of any PTB symptom, CAD4TB and Xpert MTB/RIF were also evaluated. The number of parameters to be estimated for LCA with five diagnostic tests is less than the number estimable from the degrees of freedom in the data. Hence the data could support estimation of disease prevalence and diagnostic accuracy of the five diagnostic tests. With three diagnostic tests, however, there are more parameters than degrees of freedom in the data. This introduces a statistical non-identifiability problem unless additional information enters, for instance through informative prior distributions for some parameters [8].

The dependence of sensitivity and specificity on the covariate was expressed through a Probit model. Similarly, for PTB prevalence. (Appendix A). Independent Gaussian priors $N\left(\mu ,{\sigma }^2\right)$ with unknown variance ${\sigma }^2\sim InvGamma\left(\mathit{shape}=\alpha ,rate=\beta \right)$ were used to model the uncertainty in sensitivity and specificity as well as the PTB prevalence.

Amongst the HIV− (x = 0), sensitivity and specificity were assigned a normal prior with mean of 1 on the Probit scale translating to 84% on the probability scale, for the prevalence this was mean −1 on the Probit scale translating to 16% on the probability scale. The difference in sensitivity and specificity and the difference in prevalence between the HIV− and HIV+ subpopulations were assigned priors from normal distributions with mean 0 and unknown variance. When evaluating five diagnostic tests, the variance parameters were assigned near-uninformative $InvGamma\left(1·0^{-3},1·0^{-3}\right)$ priors (Appendix A: Figs. A.3–A.13). Given the identifiability issues when evaluating three diagnostic tests, the variance parameters for prevalence, sensitivity and specificity were assigned informative $InvGamma\left(2,3\right)$ priors (Appendix A: Figs. A.14–A.20). The variance parameters of the difference in prevalence and the difference in sensitivity and specificity between the HIV− and HIV+ were assigned priors from $InvGamma\left(3,1\right)$. The values of the inverse Gamma distribution were chosen such that the variation in the estimate would span the range of plausible values for the parameter (Appendix A: Table A.6, Figs. A.1 and A.2). Marginal sensitivity, specificity and prevalence were assigned priors similar to those of the HIV− subpopulation. Given the lack of a perfect reference standard, correct informative priors for the parameters of the model may not be readily known. Nonetheless, based on expert knowledge, using the most accurate imperfect reference standard a diagnostic test that is promising for diagnosis of a disease often has a sensitivity and a specificity >50%. Thus, we chose prior distributions for sensitivity and specificity with mode around 84% on the probability scale that reflected the degree of confidence in the performance of the diagnostic tests. The prior chosen for the prevalence was based on the general understanding about the prevalence of the disease spanning a range of plausible values in the population rather than knowledge of the actual estimate.

For each replicate dataset, we calculated the median of the posterior distribution of PTB prevalence, diagnostic test sensitivity and specificity as our point estimate with the corresponding 95% credible intervals (95% CrI), defined as 2·5%–97·5% percentiles of the posterior distribution. For each combination of the four working models and three sample sizes, we calculated the median of the distribution of posterior median estimates of the one hundred replicate datasets. The corresponding 2·5% and 97·5% percentiles of the distribution of the one hundred posterior median estimates were derived. These intervals were referred to as 95% reference intervals (95% RI). We also calculated the mean and the corresponding 95% confidence intervals (95% CI) as well as the root mean squared error (RMSE) from the distribution of the one hundred posterior median estimates. Using the lower and upper estimates of the 95% CrI for each posterior distribution of the one hundred replicate datasets we derived the coverage rates. Posterior inferences were based on 50,000 Monte Carlo iterations with the first 25,000 discarded as “burn-in”. Convergence in model fitting was assessed by running three chains. In order to reduce autocorrelation between consecutive values in the chain, every 10th iteration was saved (“thinning”) [29]. Trace plots and Gelman-Rubin convergence statistic <1·05 were used to monitor mixing in the chains [30]. Trace plots for the posterior samples of the parameters obtained from analysis of the first replicate dataset of size 1000, 2000 and 5000 using working model IV are provided in Appendix A (Figs. A.21–A.22). Analysis was implemented in R version 4.0.3 using R2jags package for R version 4.0.3 [31], [32].

5. Simulation results

5.1. Pulmonary TB prevalence

In Table 1 we present the frequentist evaluation of the posterior distributions of total population pulmonary TB (PTB) prevalence. True values as presented in Table 1 in this section and in the following sections refers to the actual values used in the simulation. We present the frequentist median with 95% reference intervals (95% RI), mean with 95% confidence intervals (95% CI) and the true value of the total population PTB prevalence for five and three diagnostic tests analyzed using the four working models. We also present the root mean squared error (RMSE) and coverage rates of the 95% credible intervals (95% CrI) around the median estimates of the posterior distributions. All estimates are based on the analysis of one hundred replicate datasets. From this point going forward we refer to the coverage rates of the 95% CrI around the median estimates of the posterior distributions as coverages of the 95% CrI.

Table 1.

Frequentist evaluation of Bayesian estimates of total population pulmonary tuberculosis (PTB) prevalence obtained using four working models in the analysis of five and three diagnostic test results.

			Five diagnostic tests
Model	N	True value	Median (95% RI)	Mean (95% CI)	RMSEx100	Coverage
I	1000	6·0	6·3 (4·4, 8·9)	6·4 (6·1, 6·6)	1·2	95·0
	2000	6·0	6·1 (5·0, 7·3)	6·1 (6·0, 6·2)	0·6	95·0
	5000	6·0	6·0 (5·2, 6·9)	6·9 (5·2, 8·6)	8·8	93·0
II	1000	6·0	7·3 (5·5, 10·6)	7·5 (7·1, 7·8)	2·3	81·0
	2000	6·0	6·5 (5·1, 7·9)	6·5 (6·4, 6·6)	0·8	90·0
	5000	6·0	6·2 (5·4, 6·9)	6·2 (6·1, 6·3)	0·4	93·0
III	1000	6·0	6·4 (4·4, 11·4)	6·6 (6·3, 6·9)	1·7	94·0
	2000	6·0	6·0 (4·7, 7·4)	6·0 (5·9, 6·1)	0·7	93·0
	5000	6·0	5·9 (5·2, 6·7)	5·9 (5·9, 6·0)	0·4	95·0
IV	1000	6·0	6·7 (4·7, 9·5)	6·8 (6·5, 7·1)	1·6	93·0
	2000	6·0	6·2 (4·8, 7·7)	6·3 (6·1, 6·4)	0·7	93·0
	5000	6·0	6·1 (5·3, 6·9)	6·1 (6·0, 6·2)	0·4	94·0
			Three diagnostic tests
Model	N	True value	Median (95% RI)	Mean (95% CI)	RMSEx100	Coverage
I	1000	6·0	5·7 (3·0, 16·2)	6·6 (5·9, 7·3)	3·4	96·0
	2000	6·0	6·1 (4·0, 13·1)	6·6 (6·2, 7·1)	2·4	98·0
	5000	6·0	6·7 (4·4, 12·7)	7·3 (6·8, 7·7)	2·4	94·0
II	1000	6·0	23·1 (7·0, 39·8)	23·4 (21·7, 25·1)	19·4	17·0
	2000	6·0	23·0 (14·6, 37·3)	24·0 (22·8, 25·2)	19·0	0·0
	5000	6·0	25·5 (18·7, 36·3)	26·1 (24·8, 27·4)	21·2	0·0
III	1000	6·0	4·9 (2·7, 12·9)	5·3 (4·8, 5·8)	2·5	94·0
	2000	6·0	5·0 (3·2, 8·5)	5·3 (5·0, 5·5)	1·6	98·0
	5000	6·0	5·6 (3·8, 10·5)	5·9 (5·6, 6·2)	1·6	92·0
IV	1000	6·0	5·1 (2·9, 15·2)	5·7 (5·1, 6·4)	3·2	96·0
	2000	6·0	5·4 (3·5, 8·0)	5·5 (5·2, 5·7)	1·3	99·0
	5000	6·0	5·6 (4·1, 8·2)	5·7 (5·4, 5·9)	1·2	95·0

N – Sample size.

RI – Reference Intervals and was calculated as the 2·5% and 97·5% percentiles of the distribution of median estimates of the posterior distributions from the one hundred replicate datasets.

CI – Confidence Intervals.

RMSE – Root Mean Square Error.

Five diagnostic tests: any PTB symptom, CAD4TB, CRP, culture and Xpert MTB/RIF.

Three diagnostic tests: any PTB symptom, CAD4TB and Xpert MTB/RIF.

Model I – Model restricting PTB prevalence and the diagnostic test accuracy to remain constant across the HIV subpopulations.

Model II – Model allowing PTB prevalence but not the diagnostic test accuracy to vary across the HIV subpopulations.

Model III – Model restricting PTB prevalence but not the diagnostic test accuracy to remain constant across the HIV subpopulations.

Model IV – Model allowing PTB prevalence and the diagnostic test accuracy to vary across the HIV subpopulations.

When evaluating five diagnostic tests, the working models accounting for heterogeneity in diagnostic test performance (working models III and IV) as well as the model assuming homogeneous population produced consistent estimates of the total population PTB prevalence. There was evidence of some systematic bias for smaller sample size. The model assuming heterogeneity in PTB prevalence but constant diagnostic accuracy across the subpopulations yielded systematically biased but consistent estimates of total population PTB prevalence.

In the evaluation of three diagnostic tests, working models I and II yielded systematically biased estimates of the total population PTB prevalence. Model II yielded large RMSE and poor coverages of 95% CrI. Working models III and IV yielded consistent estimates of total population PTB prevalence with modest systematic bias.

5.2. Sensitivity and specificity of the diagnostic tests

5.2.1. Evaluation of five diagnostic tests

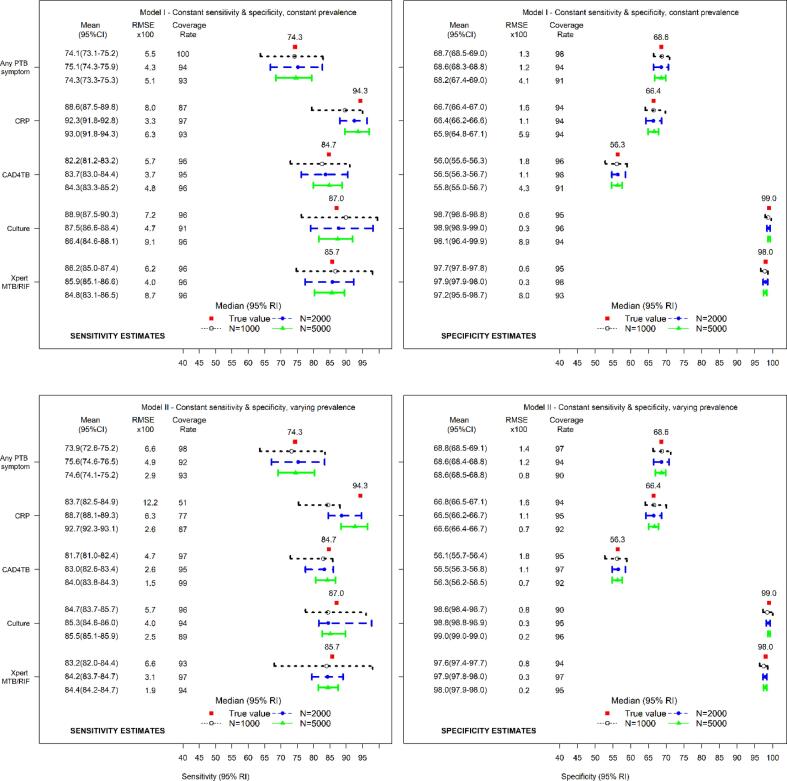
Fig. 2 presents the estimates of sensitivity and specificity for five diagnostic tests analyzed using working models I and II. The models produced asymptotically consistent estimates of the total population sensitivity and specificity with small systematic bias. The RMSE were good with acceptable coverages of the 95% credible intervals (95% CrI). Working model II, however, yielded estimates of sensitivity for CRP that were different from the true value with tendency towards the mean of prior distribution.

Fig. 2.

Median (95% reference intervals (RI)) and mean (95% confidence intervals (CI)) estimates of total population sensitivity (left) and specificity (right) with corresponding root mean squared error (RMSE) and coverages of 95% credible intervals (CrI) for true total population sensitivity and specificity for five diagnostic tests evaluated using working model I (top panel) and working model II (lower panel) – Working model I restricts the diagnostic test accuracy and disease prevalence to remain constant across the HIV subpopulations, Working model II restricts the diagnostic test accuracy to remain constant but allows the disease prevalence to vary across the HIV subpopulations.

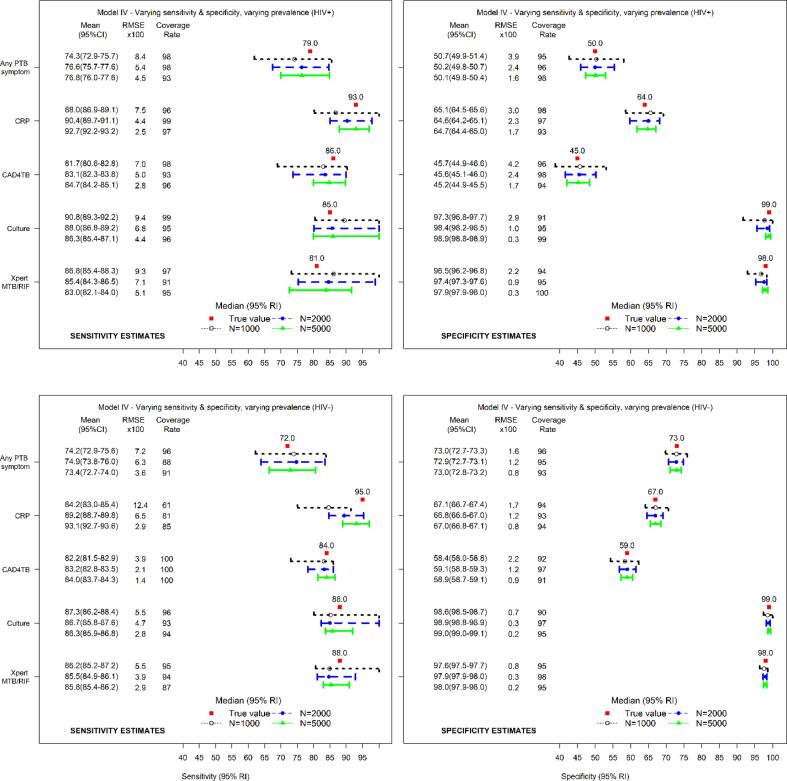
Fig. 3 presents the estimates of sensitivity and specificity by HIV status for five diagnostic tests evaluated using working model IV (true model). The model yielded estimates of sensitivity that matched the true values. The estimates of sensitivity among the HIV− were skewed in the direction of the prior. There was no evidence of serious systematic bias in the estimates of specificity. Similar findings were obtained using working model III (Fig. B.1 in Appendix B).

Fig. 3.

Median (95% reference intervals (RI)) and mean (95% confidence intervals (CI)) estimates of sensitivity (left) and specificity (right) for HIV+ (top panel) and HIV− (lower panel) with corresponding root mean squared error (RMSE) and coverages of 95% credible intervals (CrI) for true sensitivity and specificity for five diagnostic tests evaluated using the model allowing the diagnostic test accuracy and disease prevalence to vary across the HIV subpopulations (working model IV).

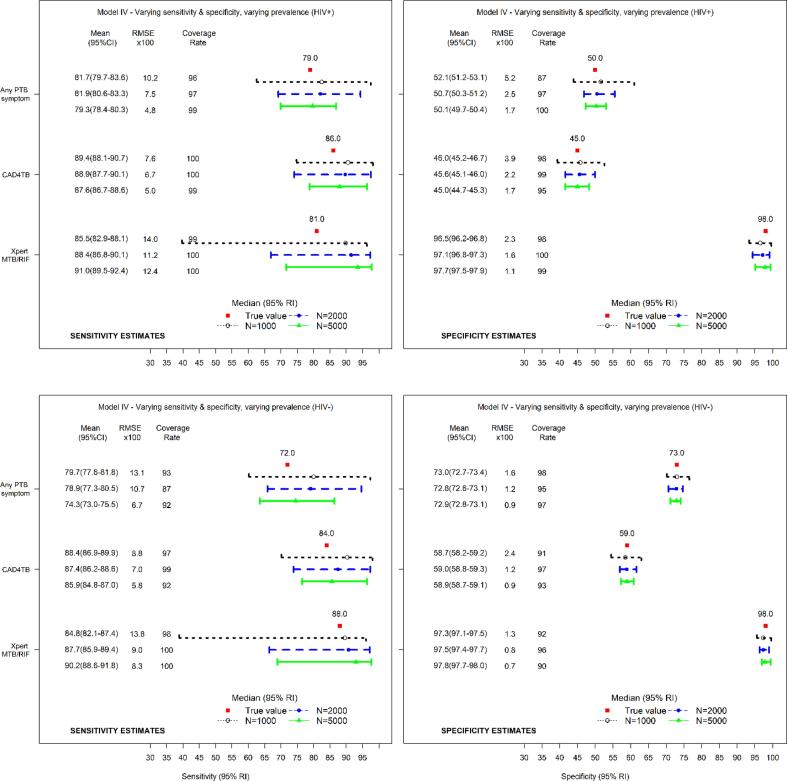
5.2.2. Evaluation of three diagnostic tests

Fig. 4 shows the estimates of sensitivity and specificity by HIV status for three diagnostic tests evaluated using working model IV (true model).

Fig. 4.

Median (95% reference intervals (RI)) and mean (95% confidence intervals (CI)) estimates of sensitivity (left) and specificity (right) for HIV+ (top panel) and HIV− (lower panel) with corresponding root mean squared error (RMSE) and coverages of 95% credible intervals (CrI) for true sensitivity and specificity for three diagnostic tests evaluated using the model allowing the diagnostic test accuracy and disease prevalence to vary across the HIV subpopulations (working model IV).

The estimates of sensitivity and specificity indicate some systematic bias. Similar findings were obtained using working model III (Fig. B.3 in Appendix B). Fig. B.2 in Appendix B shows the estimates of sensitivity and specificity for three diagnostic tests analyzed using working models I & II.

6. Discussion

Our aim was to investigate implications of violation of model assumptions induced by an observed external covariate that is associated with diagnostic test accuracy and risk of the targeted disease. We assessed some likely model violations on estimation of total population prevalence of the disease, sensitivity and specificity. We supported our results with finite sample simulations mimicking a setting of passive case-finding among presumptive pulmonary tuberculosis (PTB) patients with or without HIV. Based on realistic sensitivities and specificities of five diagnostic tests used for PTB, we simulated independent test results in samples of various sizes with different PTB prevalence within the HIV subpopulations. Due to instability of the estimates with small sample size, we endeavored to be as realistic as possible by choosing different sample sizes (1000, 2000, 5000) to help us evaluate the performance of LCA when the number of true PTB cases is as low as 60 (20 in the HIV+ and 40 in the HIV− subpopulations) when N = 1000 and when it is as high as 300 (100 in the HIV+ and 200 in the HIV− subpopulations) when N = 5000 with 6% overall TB prevalence (5% in HIV− and 10% HIV+). For five and three diagnostic tests, we performed Bayesian LCA using four working models assuming constant (or varying) PTB prevalence and diagnostic test accuracy across the HIV subpopulations. We have shown that in the analysis of five and three diagnostic tests the model ignoring heterogeneity in diagnostic test accuracy but allowing the prevalence of PTB to vary across the subpopulations (working model II) produced systematically biased estimates of total population PTB prevalence and diagnostic test accuracy. However, the models accounting for heterogeneity in diagnostic test accuracy across the subpopulations (working models III and IV) yielded consistent estimates with modest systematic bias.

Working models I and II violated the assumption of conditional independence when the diagnostic test accuracy was restricted to remain constant. When used to evaluate five diagnostic tests, working model I appeared robust to violation of the assumption of conditional independence. Working model II yielded systematically biased but consistent estimates. Working models III and IV produced consistent estimates of total population PTB prevalence and modestly biased estimates of sensitivity with greater uncertainty. The specificity estimates matched the true values while the sensitivity estimates were skewed in the direction of the prior in the HIV− subpopulation. With small sample size (few cases with PTB) Bayesian estimation is driven more by the prior rather than the likelihood. This finding emphasizes the need to carefully choose the prior distribution as alluded to by others [33], [34], [35]. An additional analysis evaluating three diagnostic tests using the same working models but different priors revealed the unavoidable dependency of the results on the (informative) prior (Table B.1 and Figs. B.4 – B.6 in Appendix B). In our analyses we chose prior distributions that reflected the degree of confidence in the performance of the diagnostic tests and the general understanding about the prevalence of the disease rather than knowledge of the actual estimate. This was intentional to avoid presuming knowledge of the performance of the diagnostic tests given the lack of a gold standard.

In the analysis of three diagnostic tests, working models I and II yielded systematically biased estimates of total population PTB prevalence. The models also produced systematically biased and highly unstable estimates of total population sensitivity. Thus, Bayesian LCA with fewer diagnostic tests that violate the assumption of constant diagnostic test accuracy across the underlying subpopulations may suffer from limited information that contribute to bias as established by others [20], [33], [34], [36]. Using working models III and IV demonstrated modest bias in the sensitivity but reliable estimates of specificity. Failure to account for varying disease prevalence in working model III did not noticeably impact the estimates of diagnostic test accuracy.

Residual dependence induced by a measured covariate remains even after conditioning analysis on the latent disease status. This leads to incorrect inferences. Potential remedies to such problems in real studies was evaluated through simulations. Though not applied to real dataset, this may not be viewed as a weakness of the study but should serve as a guide to experts intending to apply LCA to carefully consider plausibility of the model, especially in TB where severe comorbidities are known to affect diagnostic test performance. LCA uses all the available imperfect diagnostic tests, including symptoms, to determine the likelihood of the presence of PTB for an individual. Therefore, incorrectly specified model not only yields biased inferences for diagnostic test accuracy and disease prevalence but also contributes to incorrect diagnosis and treatment of cases. This has serious implications in terms of allocation of resources, unnecessary harm to individuals without the disease, and onward transmission of infectious disease by those missed due to incorrect diagnosis. Our approach reveals the need for a rigorous process that involves experts in the field of study. Besides their knowledge on the diagnostic tests known to be dependent conditional on the (unknown) disease status, their input regarding potential covariates that affect the disease prevalence as well as the diagnostic test accuracy can be harnessed and incorporated into the model. In addition, correct statistical methods can be used to evaluate the importance of the proposed covariates in influencing disease prevalence and the diagnostic test accuracy. All these ideas put together should yield a plausible model that best explains the diagnostic accuracy of the tests and the prevalence of the disease.

7. Conclusion

In the presence of measured covariates known to affect the diagnostic accuracy and disease prevalence, experts should avoid the model that allows the disease prevalence to vary but restricts the diagnostic test sensitivity and specificity to remain constant across the different subpopulations. This model yield severely biased estimates of PTB prevalence and diagnostic test accuracy. The model that allows the disease prevalence to remain constant but allows the diagnostic test sensitivity and specificity to vary across the different subpopulations yields correct estimates of overall disease prevalence (averaged across the different subpopulations) and the subpopulation specific estimates of sensitivity and specificity. The model that allows disease prevalence and diagnostic test sensitivity and specificity to vary across the different subpopulations defined by the covariates known to induce test dependence should be applied. When the interest is also to understand the drivers of disease prevalence then this model should be applied. In the absence of measured covariates or when the conditions do not allow adjusting for covariates due to small sample size (or few PTB cases), the model that allows the disease prevalence and the diagnostic test sensitivity and specificity to remain constant across the different subpopulations can be applied since it would yield less biased estimates.

In light of these findings, we recommend diagnostic studies to be as inclusive as possible in collecting important covariates known to influence diagnostic test performance e.g HIV status, history of TB treatment, miners etc. Because of the obvious concerns regarding imperfect reference standard, correctly specified latent class model should be used to evaluate new diagnostic tests as well as determine disease prevalence. Interpretation of results based on small sample sizes should be done carefully since they may lack precision. We saw a potential influence of the prior distribution on the posterior estimates of sensitivity attributed to small sample size. Therefore, correct choice of the prior for modelling uncertainty in diagnostic test sensitivity and prevalence is imperative, particularly for few diagnostic tests or small sample sizes. Different experts have applied different latent class models, some adjusting for measured covariates and others failing to do so. Therefore, following robust model evaluation, our work provides an invaluable guidance on the correct approach for analysis of imperfect diagnostic tests in the presence of a measured covariate that affects the prevalence of the disease and/or diagnostic accuracy of the tests. Thus our findings complement the findings of the already published work [37]. Future research should look into predictive models that can promptly give correct diagnosis for an individual based on clinical history, diagnostic test results and measured covariates.

Availability of data and materials

The parameters used in the simulation have been provided in Table A.1 in Appendix A. The simulation as well the analysis scripts written in R language can be obtained from the corresponding author upon request.

Funding

This work was supported by European and Developing Countries Clinical Trials Partnership (EDCTP) [RIA2018D-2489TB TRIAGE+]. This project is part of the EDCTP2 programme supported by the European Union. The findings and conclusions of this work are guaranteed by the authors and do not necessarily represent the official position of the funders.

CRediT authorship contribution statement

Alfred Kipyegon Keter: Conceptualization, Methodology, Data curation, Formal analysis, Validation, Visualization, Writing – original draft. Lutgarde Lynen: Funding acquisition, Conceptualization, Methodology, Writing – review & editing, Supervision. Alastair Van Heerden: Funding acquisition, Conceptualization, Methodology, Writing – review & editing, Supervision. Els Goetghebeur: Conceptualization, Methodology, Writing – review & editing, Supervision. Bart K.M. Jacobs: CConceptualization, Methodology, Formal analysis, Writing – review & editing, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: