Skip to main content
PMC home page
Nanoscale Advances logoLink to Nanoscale Advances
. 2018 Dec 19;1(2):546–553. doi: 10.1039/c8na00305j

Correlation between the electronic/local structure and CO-oxidation activity of PdxRu1−x alloy nanoparticles†

Chulho Song 1,§, Akhil Tayal 1,‡, Okkyun Seo 2,1, Jaemyung Kim 1, Yanna Chen 2,1, Satoshi Hiroi 2, L S R Kumara 1,, Kohei Kusada 3, Hirokazu Kobayashi 3, Hiroshi Kitagawa 3, Osami Sakata 1,2,4,✉
PMCID: PMC9473174  PMID: 36132276

Abstract

PdxRu1−x nanoparticles (NPs) were observed to display enhanced CO oxidation activity with the maximum performance obtained at the composition x = 0.5. To unveil the origin of this superior CO oxidation activity, we investigated the local structure, valence state, and electronic properties of PdxRu1−x NPs using synchrotron-based X-ray techniques. Site specific information obtained from X-ray absorption fine structure (XAFS) spectroscopy revealed that the local disorder around Pd and Ru atoms and their valence state can be systematically tuned by varying the Pd composition. Furthermore, the XAFS results indicated a strong correlation among the structural and valence state and the observed CO oxidation catalytic properties of PdxRu1−x NPs. Hard X-ray photoelectron spectroscopy (HAXPES) analysis suggested that the capability of CO oxidation requires an optimum balance between the adsorption and desorption energy for CO adsorption and eventually conversion to CO2. A comparison between the experimental valence band (VB) HAXPES spectra of PdxRu1−x NPs and the linear combination of VB HAXPES spectra of Pd and Ru NPs revealed that the charge transfer from Pd to Ru occurs in the PdxRu1−x alloy at intermediate compositions, causing electron enrichment of the Ru surface. In addition, the maximum red-shift in the edge-position relative to that of bulk Pd/Ru and high structural disorder were observed for the PdRu alloy at the intermediate composition. This coupled behavior of structure and electronic properties followed the experimental trend of CO oxidation activity in this system.

Enhanced CO oxidation activity of PdRu nanoparticles (NPs) at x = 0.5 is originated from the maximum localized disorder of Pd/Ru and the charge transfer from Pd to Ru occurs in the partial PdRu alloy.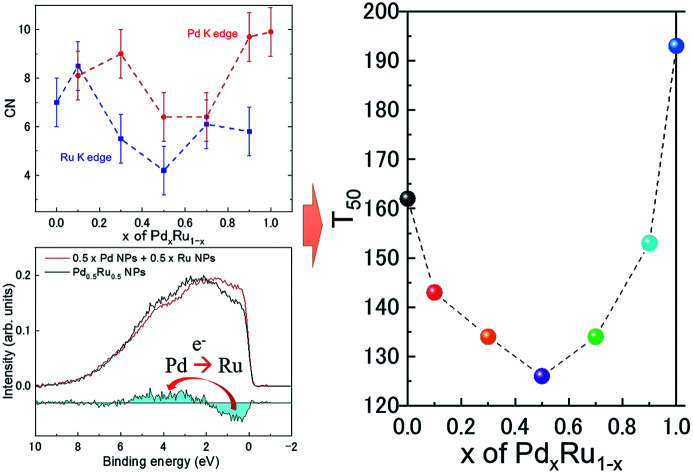graphic file with name c8na00305j-ga.jpg

1. Introduction

Bimetallic nanoparticles (NPs) have recently emerged as an important class of catalysts for reactions of petrochemical significance.1–3 Previous studies4–10 on bimetallic NP catalysts, such as Pd–Ru, Au–Pt, Ru–Cu, Pt–Ru, and Ag–Ru, have indicated that their enhanced catalytic activity arises from the synergy between the nano-sized component elements; in contrast, this phenomenon is not observed in solid solutions of two bulk metals. Among various other candidates, Ru NPs serve as an effective catalyst for various processes such as olefin metathesis,11 the oxidation of amines,12 ammonia synthesis,13 CO oxidation,14,15 and NOx reduction.15 Similarly, Pd NPs exhibit excellent properties for hydrogen storage. Pd NPs also serve as an effective catalyst for fuel-cell electrodes and exhaust-gas purification.16,17 However, the catalytic activity of Pd is constrained by surface poisoning by CO. Therefore, the development of a hybrid catalyst is desired for enhanced performance and to mitigate the limitation of an individual alloying component.

Kusada et al.4 reported that PdxRu1−x NPs exhibit enhanced CO-oxidizing catalytic activity compared with monometallic Ru and Pd NPs, with Pd0.5Ru0.5 NPs exhibiting the highest CO-oxidizing catalytic activity. However, there is a lack of research aimed at understanding the CO-oxidation activity for PdxRu1−x NPs. The catalytic activity of bimetallic materials is observed to depend on the combination of structural parameters and its electronic states. In a number of studies, enhancement of the catalytic properties was observed with reduction of the particle size.18 Furthermore, the presence of various types of structural and compositional disorder in the alloy nanoparticle could further enhance the catalytic properties owing to the presence of active metal centers. Therefore, knowledge of the local structure is useful to investigate its effect on the catalytic activity.

Another important parameter, mostly used to understand the catalytic activity in metal NPs, is the position of the d-band center. In general, as the d-band center approaches the Fermi level, strong adsorbate–metal bonding is observed. However, the formation of a strong adsorbate–metal bond causes metal surface poisoning, which eventually leads to deterioration of the catalytic performance. Therefore, a plot of the catalytic activity against its ability to form surface chemical bond follows a volcano curve, with maximum catalytic activity for intermediate adsorption energy.18,19 Thus, identification of the d-band center with varying Pd composition would help improve our understanding of the observed catalytic activity in the PdxRu1−x system. Moreover, this information would provide insight into the effect of structure and disorder on the electronic states, which could be useful in designing better catalysts.

X-ray photoelectron spectroscopy (XPS) is a useful technique to observe the electronic structure of solids.20,21 However, as described in a previous study,22 it is very difficult to detect a bulk electronic structure of NPs with a wrapping layer using the conventional XPS technique. Synchrotron-based hard X-ray photoelectron spectroscopy (HAXPES), with a high brilliance and large probing depth, is widely used to investigate the bulk electronic structure of materials25 and this type of NPs.22 The probing depth of photoelectron spectroscopy is approximately three times of electron inelastic mean free path, which depends on kinetic energy of photoelectrons.23 The scan depth of XPS is focusing on several nanometers, which mainly includes the surface electronic information. The electronic information can be obtained using HAXPES, because the kinetic energy of photoelectrons can be largely enhanced and the probing depth is tens of nanometers.24 It is possible to understand the intrinsic electronic correlation on the basis of the HAXPES results. X-ray absorption fine structure (XAFS) measurement is another powerful tool used to observe the geometric and electronic structural change of metals during a reaction in solution.

In this study, we investigated the electronic and local structure of PdxRu1−x NPs using synchrotron-based X-ray techniques including XAFS spectroscopy and HAXPES. To help unveil the origin of their CO-oxidation activity, we discuss the coordination number (CN), K-edge shift, d-band center, and valence band (VB) HAXPES spectra of the PdxRu1−x NPs.

2. Experimental

2.1. Sample preparation

We investigated PdxRu1−x NPs (x = 0, 0.1, 0.3, 0.5, 0.7, 0.9, and 1), as shown in Table 1. For a typical synthesis of PdxRu1−x NPs (x = 0.5), poly(N-vinyl-2-pyrrolidone) (PVP, 444 mg, MW ≈ 40 000, Wako) was dissolved in triethylene glycol (TEG, 100 mL, Wako), and the solution was heated to 200 °C in air with magnetic stirring. Meanwhile, K2[PdCl4] (163.4 mg, Aldrich) and RuCl3·nH2O (131.1 mg, Wako) were dissolved in deionized water (40 mL). The resulting aqueous mixture solution was then slowly added to the TEG solution, which was maintained at 200 °C during the addition for 20–40 min. After cooling to room temperature, the prepared NPs were separated by centrifugation. The other PdxRu1−x (x = 0.1, 0.3, 0.7, and 0.9) NPs were prepared by controlling the molar ratio of the Pd2+ and Ru3+ ions. The details of the determination of the NP size from the size histograms, TEM images (ESI Fig. S1†), and temperature for 50% conversion of CO to CO2 (T50) are also described in ESI Note A and B.†

Reaction conditions for syntheses of PdxRu1−x NPs.

Sample K2[PdCl4]/mg RuCl3·nH2O/mg TEG/mL PVP/mmol
Ru 783.2 50 1.0
Pd10Ru90 32.6 235.6 100 10.0
Pd30Ru70 98.0 180.3 100 1.0
Pd50Ru50 163.4 131.1 100 1.0
Pd70Ru30 228.7 62.4 100 1.0
Pd90Ru10 293.8 25.9 100 1.0
Pd 326.3 100 5.0
Open in a new tab

2.2. XAFS experiments

XAFS measurements of the Pd K-edge (24.35 keV) and Ru K-edge (22.12 keV) were performed using a Si (311) double-crystal monochromator at beamline BL01B1 of SPring-8, Japan. All the XAFS spectra were obtained in transmission mode at room temperature. The powder samples were used to fill the hole of a 0.5 mm-thick copper plate using Kapton tape on both sides. The inner diameter of the hole was 3.0 mm. The intensities of the incident and transmitted X-ray beams were collected using ionization chambers located in front and behind the respective samples. Pre-edge and post-edge background subtraction were performed following the standard procedure.26 The extraction of extend X-ray absorption fine structure (EXAFS) signals was performed by subtracting an atomic background, which was simulated using a polynomial spline function. The knot positions of the spline were optimized to minimize the signal in the Fourier transform between 0–1 Å. The EXAFS data were fitted using a non-linear least square fit in the k-range of 3–13.7 Å−1 and R-range of 1–3 Å. Estimation of the backscattering amplitude and phase-shift were performed using the FEFF7 code.27 All the data were processed using the software written by Conradson et al.28

2.3. HAXPES experiments

HAXPES measurements were performed by employing a linearly polarized X-ray beam in the horizontal plane with a photon energy of 5.95 keV at the undulator beamline BL15XU of the National Institute for Materials Science (NIMS) at SPring-8 in Japan. The total energy resolution was estimated to be 240 meV with a pass energy of 200 eV using a standard Au sample. All the HAXPES spectra were measured at room temperature. To eliminate the charge-up phenomenon, all the NPs were mixed with carbon powder.

3. Results and discussion

3.1. Local structure: EXAFS

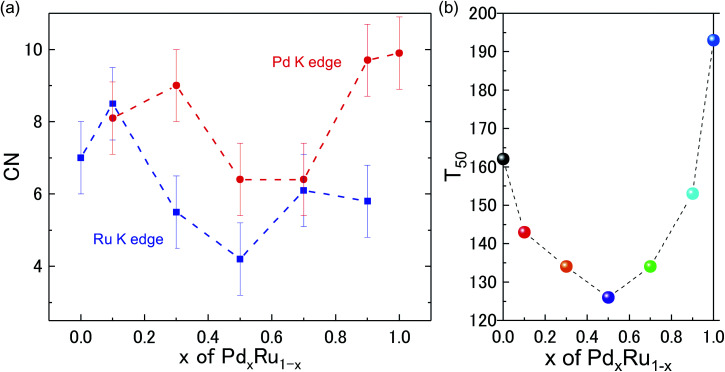
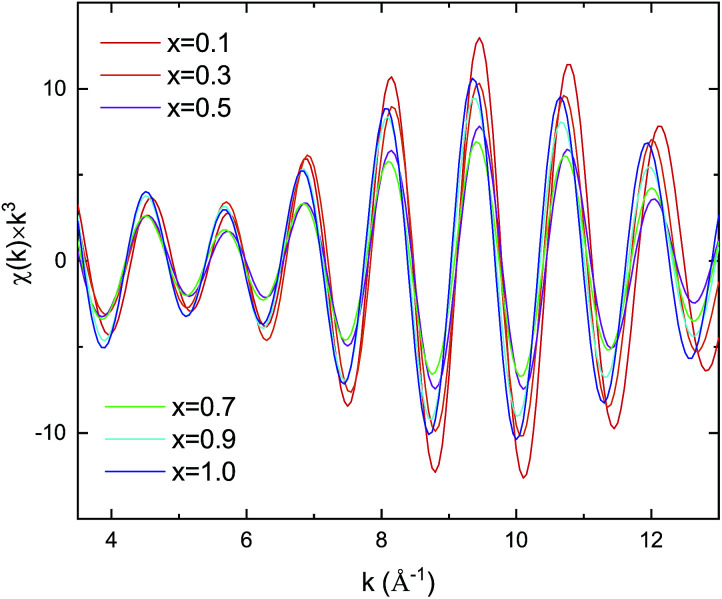
Kusada et al.4 previously showed that the CO-oxidation activity can be tuned by varying the Pd composition in the PdxRu1−x NP alloy system (see Fig. 1(b)). To understand the role of the nanoparticle structure on the observed catalytic properties, we investigated the local structure of PdxRu1−x NPs. The local structure parameters such as the first-shell bond distance (R), coordination number (CN), and root-mean-square displacement (σ) were derived using a least-squares fit of the EXAFS data. The obtained metrical parameters are tabulated in ESI Table T1† and are plotted in ESI Fig. S2.†Fig. 1(a) shows the variation in the first shell CN obtained from the EXAFS measurements at the Ru K-edge and Pd K-edge as a function of Pd composition (x). For all the samples, the CN was lower than the crystallographic bulk value of 12. A typical error of 10–20% was observed for CN, as shown in the figure. Minimum values of the CNs around Pd/Ru were observed at x = 0.5. CN and σ are known to be correlated in the EXAFS fit; however, these parameters produce a distinct effect on a chi (χ) spectrum. Generally, the χ amplitude falls more rapidly in the high-k region than in the low-k region with increasing Debye–Waller factor.29 In contrast, a uniform reduction in the χ amplitude occurs over the entire k region with decreasing CN. Fig. 2 presents a back-transform of the FT spectra measured at the Pd K-edge in the region, dominated by the first coordination shell (R–ϕ = 1.7–3 Å). The corresponding amplitude envelope is also shown in Fig. 2. The χ amplitude falls uniformly in the entire k range for all the spectra. These results indicate that increasing the Pd composition has a dominant effect on the CN. In addition, the χ amplitude decreases monotonically for x = 0.1–0.7 and later increases at x = 0.9 and 1.0. This trend correlates with the observed trend in the CNs shown in Fig. 1(a). Using the Rietveld refinement method for synchrotron-XRD patterns described in previous work,4 we determined the domain size of the two crystallographic phases (hcp + fcc) to confirm the relationship between the CN and domain size. The values are tabulated in Table 2. The main contribution of the hcp phase is from crystallographic nature of Ru, whereas an fcc component is related to the crystallographic nature of Pd.

Fig. 1. (a) First shell coordination number for Ru K-edge (blue closed squares) and Pd K-edge (red closed circles) for PdxRu1−x NPs as a function of x. (b) Catalytic activity T50 as a function of x. Here, T50 means the temperature for 50% conversion of CO to CO2.

Fig. 1

Open in a new tab

Fig. 2. Pd–Pd k3χ(k) spectra and amplitude after back-transform of FT spectra.

Fig. 2

Open in a new tab

Average crystalline domain sizes of two crystallographic phases (hcp + fcc) for PdxRu1−x NPs obtained using the Rietveld refinement method4.

Sample hcp fcc
Ru 11.6
Pd0.1Ru0.9 9.7
Pd0.3Ru0.7 7.5 4.9
Pd0.5Ru0.5 3.8 3.4
Pd0.7Ru0.3 2.0 4.5
Pd0.9Ru0.1 10.6
Pd 11.8
Open in a new tab

As observed in Table 2, the domain size of the hcp phase decreases with decreasing Ru content; the XRD data for Pd0.9Ru0.1 NPs could reasonably be refined with the single fcc phase. The domain size of the fcc phase showed a similar trend of decreasing domain size with decreasing Pd composition. Furthermore, the XRD data for the Pd0.1Ru0.9 NPs could also be refined with the single hcp phase. This monotonic decrease in the domain size for both the fcc and hcp phases differs greatly from the observed variation of CN as a function of x for the EXAFS analysis (see Fig. 1 and 2). As such it was observed that a decrease in the particle size was concomitant with reduction in the CN.30 Thus, a minimum CN was expected for Ru at x = 0.7 and for Pd at x = 0.5. However, the minimum CN values obtained from the EXAFS analysis were observed at x = 0.5 for Ru and at x = 0.5 and 0.7 for Pd (the XRD crystallize size differed for these samples). These results indicate that there is no clear correlation between the CN and domain size, suggesting that the reduction in the CNs is not solely related to the obtained crystallographic domain size.

The EXAFS technique has been frequently employed to estimate the CN of NPs with varying sizes and shapes.30 Marinkovic et al.31 observed a reduction of 30–40% in the CN of monoatomic Rh and Pt for particle sizes of 1–2 nm. Recently, considerable efforts have been focused on determining CN theoretically in NPs for a given cluster model. A compilation of results obtained using different modeling approaches was provided by Frenkel et al.30 Some level of similarity was observed in the estimation of CN for the fcc cuboctahedral particles using different approximations, with the most convincing results obtained using the method proposed by Jentys.32 Notably, the CNs calculated using different theoretical approaches displayed the most similarity for the first shell. Even after adopting different strategies, the CN of the first shell was only reduced by 30–40% for NPs of size 1–2 nm. However, for the present case, the lowest crystallite sizes were approximately 2 nm for Ru at x = 0.7 and 3.4 nm for Pd at x = 0.5. If all the Ru and Pd clusters have dimension similar to the calculated crystallite sizes, the obtained CN value is smaller than expected. This finding suggests that other factors such as sample heterogeneity, presence of smaller sized clusters, intra/interparticle disorder, and compositional disorder associated with the bi-metallic system could contribute to the obtained anomalous reduction in the CN.

Because the EXAFS technique could not distinguish among the Ru–Ru/Pd–Pd/Ru–Pd pairs, any effect of the variation in the composition would be minimal on the EXAFS signal. Therefore, the observed reduction in the value of CN can be attributed to the heterogeneity in the samples created by the formation of hcp/fcc/PdRu alloy clusters of varying size/structure distributed inhomogeneously in the samples. In addition, the value of crystallite size determined using the diffraction method indicates that the CN value should be closer to the bulk value; however, particle size information for any subnanometer clusters containing Ru and Pd atoms is limited using this technique. In contrast, any contribution from smaller sized clusters sharing the Ru and Pd atoms will be reflected in the EXAFS signal if their mass fraction is higher in the sample. Although, Ru and Pd are immiscible elements; however, in an earlier study, the formation of a solid-solution phase was observed in the elemental maps,4 but the signature of any other crystalline structure was not observed. This finding indicates that apart from the presence of hcp/fcc NPs clusters, the PdRu alloy phase could also be present in the form of smaller sized clusters. From the EXAFS fits, we observed marginal variation in the atomic pair distance at the Ru and Pd K-edge with composition (Table S1†). This result suggests that these smaller sized clusters could have an anharmonic distribution of bond lengths, creating overall structural disorder in the NPs. Thus, the anomalous reduction of CN originates from the presence of varying sizes of smaller clusters of either aggregates of Ru and Pd atoms or Pd–Ru solid solution phase. Notably, the CN follows a downturn pattern with the minima at the 50 : 50 composition, which correlates with the variation of the catalytic activity as a function of x in Fig. 1(b). This finding indicates that the structural disorder created in the samples, either because of heterogeneity in the NP cluster sizes or by the formation of disordered smaller sized clusters of PdRu alloy phase, was maximum at the 50 : 50 composition. The maximum disorder at this optimum composition could also be a source of highly active sites with different electronic properties than those of individual Pd/Ru NPs, resulting in the observed behavior of CO oxidation and a highly catalytically active material.

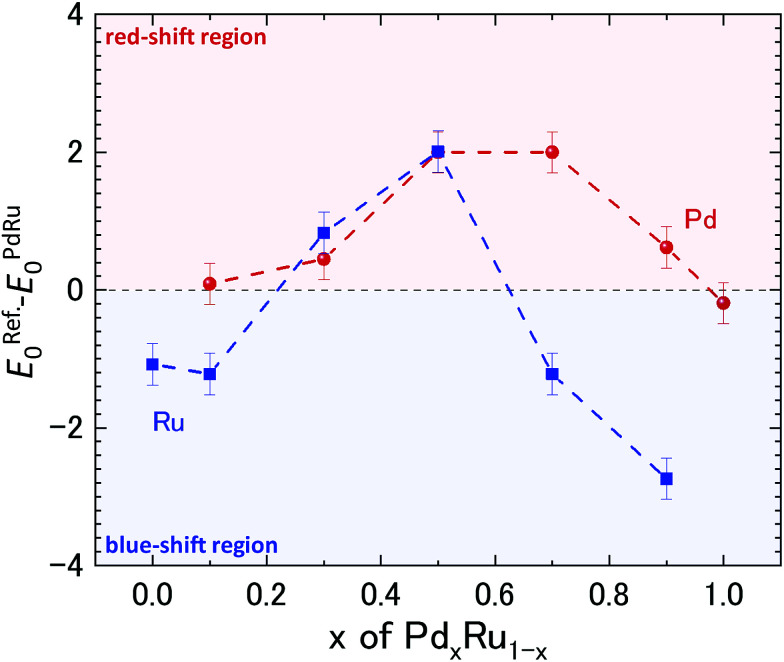
To gain further insight into the role of the valence state on the catalytic properties, X-ray absorption near edge structure (XANES) analysis was performed. The measured XAFS spectra at the Ru and Pd K-edges are plotted in ESI Fig. S3.†Fig. 3 shows the shift in the edge position relative to that of the Pd and Ru references obtained from the measured spectra, as shown in ESI Fig. S3.† For Ru, Pd0.1Ru0.9, Pd0.7Ru0.3, and Pd0.9Ru0.1 NPs, the edge position of the Ru K-edge shifted to a higher energy (blue shift), suggesting partial oxidation of the Ru in the NPs. In contrast, the edge position of the Ru K-edge for the Pd0.3Ru0.7 and Pd0.5Ru0.5 NPs shifted to a lower energy (red shift), indicating a partial reduction of Ru in the NPs. No blue shift is apparent in the XAFS spectra of the Pd K-edge. Namely, all the samples either showed no red shift or a significant red shift. The maximum red shift of the Pd K-edge was observed for the Pd0.5Ru0.5 and Pd0.7Ru0.3 NPs. For the Ru K-edge, the maximum red shift was observed for the Pd0.5Ru0.5 NPs, and a slightly lower red shift was observed for the Pd0.3Ru0.7 NPs. In addition, the Pd0.5Ru0.5 NPs showed the maximum red shift at both the Ru and Pd K-edge. The observed upturn pattern of the edge position as a function of Pd composition can be correlated to the downturn of CN and T50 in Fig. 1. The following conclusions can be drawn from these results: (1) the localized disorder around Pd and Ru resulting from sample heterogeneity and the formation of the small sized clusters of PdRu solid-solution phase actively governs the catalytic properties of the Pd–Ru alloy and (2) the red-shift in the valence state of both Ru and Pd at the optimum composition signifies charging of the NPs, which is highly correlated with the CO oxidation behavior. Moreover, optimum values of these parameters are obtained for the Pd0.5Ru0.5 NPs. The formed disorder structure and PdRu alloy clusters of varying sizes are expected to result in unique electronic properties compared with those of individual Pd and Ru NPs. Thus, the PdRu alloy NPs act as a source of highly active sites for CO conversion unlike the separate Pd and Ru NPs. Theoretical (DFT+U) calculations on the Au-based bi-metallic system Au–X (X = Ag, Cu, Pd, Pt, Rh, Ru)33 indicated that high catalytic activity in the bimetallic system occurs when the reactants do not compete for binding sites at the NP surface. In the present case, it can be deduced that a larger volume fraction of highly active atomic sites available for CO conversion is present for the Pd0.5Ru0.5 NPs than for the other Pd compositions. Consequently, there is less competition for absorption of O2 and CO than for the samples with other Pd compositions, leading to the observed high catalytic properties at the x = 0.5 composition. The obtained XAFS results demonstrate the strong correlation of the structural and valence state with the observed CO-oxidation catalytic properties of the PdxRu1−x system. To investigate the effect of the electronic structure on the CO oxidation, we further performed HAXPES measurements for the PdxRu1−x NPs, and the related analysis is provided in the next section.

Fig. 3. Relative shift in the edge position of Ru K-edge and Pd K-edge as a function of Pd content (x). The edge positions measured at the Ru K-edge and Pd K-edge were subtracted from those of Ru and Pd metal references, respectively.

Fig. 3

Open in a new tab

3.2. Electronic structure: HAXPES

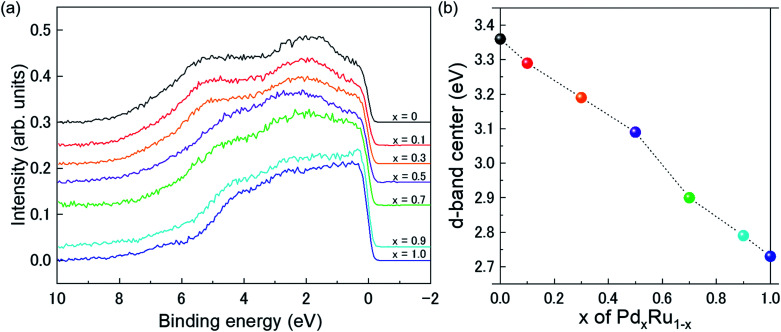
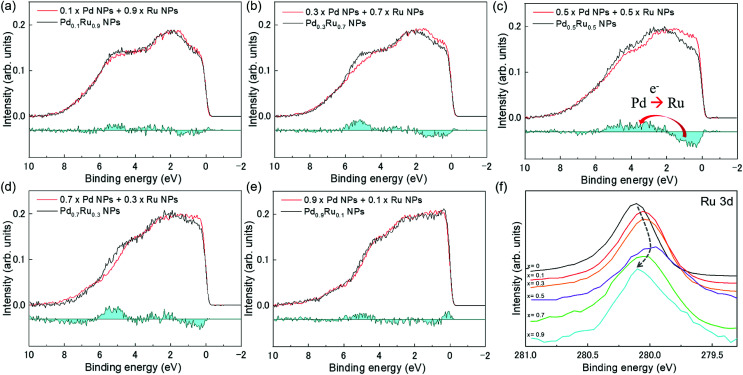
Fig. 4(a) presents VB HAXPES spectra of the PdxRu1−x NPs (x = 0, 0.1, 0.3, 0.5, 0.7, 0.9, 1). To ensure a valid comparison among the VB HAXPES spectra, the following steps were performed: (1) the background caused by carbon powder was subtracted, (2) the areas of all the VB HAXPES spectra were measured in the same region (0–10 eV), and the VB spectrum obtained at step 2 was normalized using the spectrum area. It is noted that the Pd NPs were more distributed than the Ru NPs for peak intensity in the range of −0.2 to 2.0 eV and the Ru NPs were more distributed than the Pd NPs for peak intensities in the range of 4.3–8.0 eV (see ESI Fig. S4†). Generally, the activity of metal catalysts is known to strongly depend on their CN. Hammer et al.34 proposed the so-called d-band model to explain trends in the catalytic activities of metal surfaces, films, and clusters. They also reported34 that the d-band center tends to move away from EF with decreasing CN. The strength of the interaction and the occupancy of the resulting states, which are directly related to the potential barrier for adsorption, are reflected by the position of the d-band center.35 The d-band centers Ēd band for PdxRu1−x NPs were evaluated using the following equation: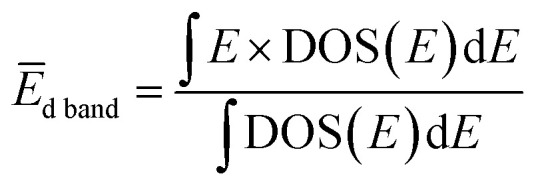3.2.where E is a binding energy and DOS(E) is the density of states of the occupied d states. The observed d-band center is expressed as follows since the photonic cross section of the s band is an approximately tenth of that of d band and accordingly the s band gives a small contributes to the valence band spectrum compared with the d band.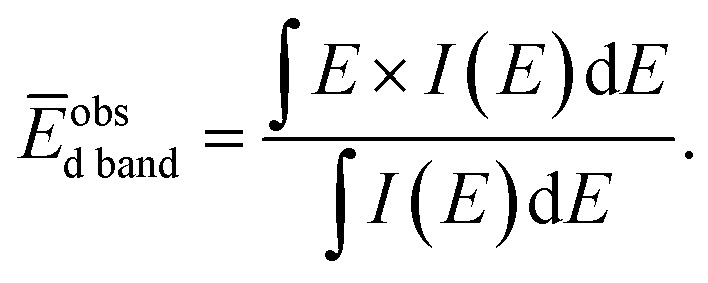3.2.

Fig. 4. (a) VB HAXPES spectra of PdxRu1−x NPs (x = 0, 0.1, 0.3, 0.5, 0.7, 0.9, 1). (b) Center of gravity of VB spectra as a function of Pd content (x).

Fig. 4

Open in a new tab

Here I(E) is an observed intensity of a valence band. Fig. 4(b) shows the d-band center (center of gravity of the VB spectra) as a function of the amount of Pd (x). It is apparent that the d-band center linearly decreased with increasing amount of Pd (x). Namely, the d-band center position shifted toward EF as x increased. However, the highest CO oxidation activity was observed for the PdxRu1−x NPs, which exhibited an intermediate d-band center. This result suggests that for CO oxidation capability, an optimum balance of the adsorption and desorption of CO is required, as reported in a previous study35 related to CO adsorption energy.

To confirm whether the prepared PdxRu1−x system is a simple physical mixture of Pd and Ru NPs or forms a partial chemical mixture/alloy from an interaction between them, we compared the experimental VB HAXPES spectra of the PdxRu1−x NPs with the linear combination of the VB HAXPES spectra of Pd and Ru NPs, as shown in Fig. 5(a)–(e). The deviation of the experimental VB spectra from the calculated VB spectra is shown in the cyan areas, which indicates an interaction between the Pd and Ru NPs and not a simple physical mixture. We presume that an intensity of inelastic scattering or secondary electrons contributing in background should be negligible compare with the Pd–Ru interaction intensity. As observed in Fig. 5(a)–(e), the deviation was largest at x = 0.5 (∼9% of total VB area) and decreased moving away from x = 0.5. This finding indicates that the formation of the partial chemical mixture/alloy reached a maximum at x = 0.5 in the PdxRu1−x system. The variation of the Ru 3d core-level as a function of the amount of Pd (x) in Fig. 5(f) also indicates that the position of the 3d core-level at x = 0.5 moved to the lowest binding energy. These results suggest that the magnitude of these deviations is closely related to the capability of CO oxidation for PdxRu1−x NPs. As mentioned above, the peak intensity in the ranges of −0.2 to 2.0 eV and in 4.3–8.0 eV mainly originates from the nature of Pd and Ru, respectively. Namely, charge transfer from Pd to Ru occurs in the partial PdxRu1−x alloy, leading to electron enrichment of the Ru atoms, which could accelerate the CO oxidation. The structural and electronic information obtained in the present study will contribute to the design and improvement of the functionality of bimetallic NPs.

Fig. 5. Comparison between experimental VB HAXPES spectra (black lines) of PdxRu1−x NPs and linear combination (red lines) for VB HAXPES spectra of Pd and Ru NPs: (a) x = 0.1, (b) x = 0.3, (c) x = 0.5, (d) x = 0.7, and (e) x = 0.9. Here, the cyan areas indicate deviation of the experimental VB spectra from the calculated VB spectra. (f) Ru 3d core-level for PdxRu1−x NPs.

Fig. 5

Open in a new tab

4. Conclusions

We investigated the local and electronic structure of PdxRu1−x NPs using synchrotron-based X-ray techniques to unveil the origin of their CO oxidation activity. The X-ray absorption fine structure spectroscopy (XAFS) studies revealed the follows: (1) the local disorder/valence state in the PdxRu1−x can be tuned by varying the Pd composition. (2) The CN or localized disordering of Pd and Ru actively governs their valence state. (3) The valence state is closely related to the CO oxidation behavior. The d-band center study, from hard X-ray photoelectron spectroscopy (HAXPES), revealed that the capability of CO oxidation needs to an optimum balance in the adsorption and desorption of CO, related to CO adsorption energy. Last, difference between the experimental VB HAXPES spectra of PdxRu1−x NPs and the linear combination for VB HAXPES spectra of Pd and Ru NPs revealed that the electron enrichment of the Ru surface, due to the charge transfer from Pd to Ru, could accelerate the CO oxidation. Hopefully, these findings will be helpful in understanding the correlation between CO oxidation activity and electronic/crystal structure parameters in new functional bimetallic NPs.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

NA-001-C8NA00305J-s001

Acknowledgments

This work was partly supported by ACCEL (JPMJAC1501) of the Japan Science and Technology Agency (JST). The XAFS measurements were performed at SPring-8 with the approval of the Japan Synchrotron Radiation Research Institute under Proposal No. 2016B1033. The HAXPES spectra were obtained at the NIMS synchrotron X-ray station of SPring-8 under Proposal No. 2012B4907, 2016B4910, and 2017A4910. The XRD measurements were performed at SPring-8 with the approval of the Japan Synchrotron Radiation Research Institute under Proposal No. 2016A1028, 2016B0134, and 2017A0134. This work was also partly supported by the Ministry of Education, Culture, Sports, Science and Technology of Japan (OS: 15K04616 and 18K04868). The authors would like to thank Tiffany Jain, M. S., from Edanz Group (http://www.edanzediting.com/ac) for editing a draft of this manuscript.

†

Electronic supplementary information (ESI) available: Particle size distributions of PdxRu1−x NPs, temperature for 50% conversion of CO to CO2 (T50) for PdxRu1−x NPs, fitting results of EXAFS, XANES analysis, VB HAXPES spectra for Ru NPs and Pd NPs (Fig. S1–S4, Table T1). See DOI: 10.1039/c8na00305j

References

  1. Wu D. Kusada K. Kitagawa H. Sci. Technol. Adv. Mater. 2016;17:583–596. doi: 10.1080/14686996.2016.1221727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Louis C. Catalysts. 2016;6:110. doi: 10.3390/catal6080110. [DOI] [Google Scholar]
  3. Principles and practice of heterogeneous catalysis, ed. J. Thomas and W. Thomas, Wiley-VCH, Weinheim, 1997 [Google Scholar]
  4. Kusada K. Kobayashi H. Ikeda R. Kubota Y. Takata M. Toh S. Yamamoto T. Matsumura S. Sumi N. Sato K. Nagaoka K. Kitagawa H. J. Am. Chem. Soc. 2014;136:1864–1871. doi: 10.1021/ja409464g. [DOI] [PubMed] [Google Scholar]
  5. Doherty R. P. Krafft J.-M. Méthivier C. Casale S. Remita H. Louis C. Thomas C. J. Catal. 2012;287:102–113. doi: 10.1016/j.jcat.2011.12.011. [DOI] [Google Scholar]
  6. Zhou S. Jackson G. Eichhorn B. Adv. Funct. Mater. 2007;17:3099–3104. doi: 10.1002/adfm.200700216. [DOI] [Google Scholar]
  7. Huang B. Kobayashi H. Yamamoto T. Matsumura S. Nishida Y. Sato K. Nagaoka K. Kawaguchi S. Kubota Y. Kitagawa H. J. Am. Chem. Soc. 2017;139:4643–4646. doi: 10.1021/jacs.7b01186. [DOI] [PubMed] [Google Scholar]
  8. Chen D. Li Y. Liao S. Su D. Song H. Li Y. Yang L. Li C. Sci. Rep. 2015;5:11604. doi: 10.1038/srep11604. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Nashner M. S. Frenkel A. I. Adler D. L. Shapley J. R. Nuzzo R. G. J. Am. Chem. Soc. 1997;119:7760–7771. doi: 10.1021/ja971039f. [DOI] [Google Scholar]
  10. Shan D. Zhou H. Zhang C. Xie C. Chen Z. Ye T. Kuang Y. ECS Electrochem. Lett. 2014;3:H20–H23. doi: 10.1149/2.0061408eel. [DOI] [Google Scholar]
  11. Weskamp T. Schattenmann W. C. Spiegler M. Herrmann W. A. Angew. Chem., Int. Ed. 1998;37:2490–2493. doi: 10.1002/(SICI)1521-3773(19981002)37:18<2490::AID-ANIE2490>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
  12. Yamaguchi K. Mizuno N. Angew. Chem., Int. Ed. 2003;42:1480–1483. doi: 10.1002/anie.200250779. [DOI] [PubMed] [Google Scholar]
  13. Jacobsen C. J. Dahl S. Hansen P. L. Törnqvist E. Jensen L. Topsøe H. Prip D. V. Møenshaug P. B. Chorkendorff I. J. Mol. Catal. A: Chem. 2000;163:19–26. doi: 10.1016/S1381-1169(00)00396-4. [DOI] [Google Scholar]
  14. Perkas N. Teo J. Shen S. Wang Z. Highfield J. Zhong Z. Gedanken A. Phys. Chem. Chem. Phys. 2011;13:15690–15698. doi: 10.1039/C1CP21870K. [DOI] [PubMed] [Google Scholar]
  15. Bowker M. Chem. Soc. Rev. 2008;37:2204–2211. doi: 10.1039/B719206C. [DOI] [PubMed] [Google Scholar]
  16. Xiao L. Zhuang L. Liu Y. Lu J. Abruña H. D. J. Am. Chem. Soc. 2009;131:602–608. doi: 10.1021/ja8063765. [DOI] [PubMed] [Google Scholar]
  17. Newton M. A. Belver-Coldeira C. Martínez-Arias A. Fernández-García M. Nat. Mater. 2007;6:528. doi: 10.1038/nmat1924. [DOI] [PubMed] [Google Scholar]
  18. van Bokhoven J. A. Miller J. T. J. Phys. Chem. C. 2007;111:9245–9249. doi: 10.1021/jp070755t. [DOI] [Google Scholar]
  19. Méndez J. López M. F. Martín-Gago J. A. Chem. Soc. Rev. 2011;40:4578–4590. doi: 10.1039/C0CS00161A. [DOI] [PubMed] [Google Scholar]
  20. Seah M. P. Dench W. A. Surf. Interface Anal. 1979;1:2–11. doi: 10.1002/sia.740010103. [DOI] [Google Scholar]
  21. Kim H. S. Kang M. Song M. W. Park J. W. Min B. R. React. Kinet. Catal. Lett. 2004;81:251–257. doi: 10.1023/B:REAC.0000019430.25850.9d. [DOI] [Google Scholar]
  22. Yang A. Sakata O. Kusada K. Yayama T. Yoshikawa H. Ishimoto T. Koyama M. Kobayashi H. Kitagawa H. Appl. Phys. Lett. 2014;105:153109. doi: 10.1063/1.4896857. [DOI] [Google Scholar]
  23. Tanuma S. Pwell C. Penn D. Surf. Interface Anal. 2011;43:689–713. doi: 10.1002/sia.3522. [DOI] [Google Scholar]
  24. Very high resolution photoelectron spectroscopy, ed. S. Húfner, Springer-Verlag, Berlin Heiselberg, 2007 [Google Scholar]
  25. Kobayashi K. Yabashi M. Takata Y. Tokushima T. Shin S. Tamasaku K. Miwa D. Ishikawa T. Nohira H. Hattori T. Sugita Y. Nakatsuka O. Sakai A. Zaima S. Appl. Phys. Lett. 2003;83:1005–1007. doi: 10.1063/1.1595714. [DOI] [Google Scholar]
  26. EXAFS Spectroscopy: Techniques and Applications, ed. B. K.Teo and D. C. Joy, Springer, US, 1981 [Google Scholar]
  27. Zabinsky S. I. Rehr J. J. Ankudinov A. Albers R. C. Eller M. J. Phys. Rev. B: Condens. Matter Mater. Phys. 1995;52:2995–3009. doi: 10.1103/PhysRevB.52.2995. [DOI] [PubMed] [Google Scholar]
  28. Conradson S. D. Durakiewicz T. Espinosa-Faller F. J. An Y. Q. Andersson D. A. Bishop A. R. Boland K. S. Bradley J. A. Byler D. D. Clark D. L. Conradson D. R. Conradson L. L. Costello A. L. Hess N. J. Lander G. H. Llobet A. Martucci M. B. Mustre de Leon J. Nordlund D. Lezama-Pacheco J. S. Proffen T. E. Rodriguez G. Schwarz D. E. Seidler G. T. Taylor A. J. Trugman S. A. Tyson T. A. Valdez J. A. Phys. Rev. B: Condens. Matter Mater. Phys. 2013;88:115135. doi: 10.1103/PhysRevB.88.115135. [DOI] [Google Scholar]
  29. Frenkel A. I. Hills C. W. Nuzzo R. G. J. Phys. Chem. B. 2001;105:12689–12703. doi: 10.1021/jp012769j. [DOI] [Google Scholar]
  30. Frenkel A. I. Yevick A. Cooper C. Vasic R. Annu. Rev. Anal. Chem. 2011;4:23–39. doi: 10.1146/annurev-anchem-061010-113906. [DOI] [PubMed] [Google Scholar]
  31. Marinković N. S. Sasaki K. Adžić R. R. Zast. Mater. 2016;57:101–109. [Google Scholar]
  32. Jentys A. Phys. Chem. Chem. Phys. 1999;1:4059–4063. doi: 10.1039/A904654B. [DOI] [Google Scholar]
  33. Zhang L. Kim H. Y. Henkelman G. J. Phys. Chem. Lett. 2013;4:2943–2947. doi: 10.1021/jz401524d. [DOI] [PubMed] [Google Scholar]
  34. Hammer B. Nørskov J. Adv. Catal. 2000;45:71–129. [Google Scholar]
  35. Abe H. Yoshikawa H. Umezawa N. Xu Y. Saravanan G. Ramesh G. V. Tanabe T. Kodiyath R. Ueda S. Sekido N. Yamabe-Mitarai Y. Shimoda M. Ohno T. Matsumoto F. Komatsu T. Phys. Chem. Chem. Phys. 2015;17:4879–4887. doi: 10.1039/C4CP03406F. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

NA-001-C8NA00305J-s001
NA-001-C8NA00305J-s001.pdf (1.5MB, pdf)

Articles from Nanoscale Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES