Human and machine similarity judgments in forensic firearm comparisons

Abstract

It is unclear whether humans assess similarity differently than automated algorithms in firearms comparisons. Human participants (untrained in firearm examination) were asked to assess the similarity of pairs of images (from 0 to 100). A sample of 40 pairs of cartridge casing 2D-images was used. The images were divided into 4 groups according to their similarity as determined by an algorithm. Humans were able to distinguish between matches and non-matches (both when shown the 2 middle groups, as well as when shown all 4 groups). Thus, humans are able to make high-quality similarity judgments in firearm comparisons based on two images. The humans' similarity scores were superior to the algorithms' scores at distinguishing matches and non-matches, but inferior in assessing similarity within groups. This suggests that humans do not have the same group thresholds as the algorithm, and that a hybrid human-machine approach could provide better identification results than humans or algorithms alone.

1. Introduction

Forensic pattern-matching methods depend on determining the similarities and differences between samples, such as a cartridge case from a crime scene and another that was fired by a suspect's firearm. Recently, it has been suggested that for many tasks machine algorithms could be utilized to do these comparisons rather than human examiners [1].

However, it is unknown whether and to what extent humans and machine algorithms assess similarity differently [2]. There is a need to evaluate the performance ability and accuracy of machine algorithms and human examiners in the different stages of a firearm comparison. Incorporating machine algorithms into forensic comparisons must be sensitive to human strengths and weaknesses. Machines should replace humans where algorithms are better, but not where algorithms are worse than humans.

Forensic firearm comparison depends on the ability to assess similarity between pieces of evidence, such as pairs of bullet cartridge cases. Indeed, according to the Association of Firearm and Tool Mark Examiners (AFTE) guidelines, to determine whether the marks on two cartridges were produced by the same firearm the examiner must decide whether the surface contours of the two cartridges are in “sufficient agreement” [3]. Thus, it is important to compare humans and machines in their performance in assessing similarity in firearms samples.

The aim of this study is to investigate whether the measures of similarity obtained by humans that are not trained in firearm comparisons (novices) are different than those obtained by a machine algorithm. Categorical data conclusions, (e.g., identification, elimination, and inconclusive) does not provide the fine-grained information about similarity rating that can help decide how to best combine human and machine in forensic comparisons. Thus, this study uses a fine-grained scale from 0 to 100. This study compares similarity ratings of breech face 2D images between untrained humans and a machine algorithm. A continuous scale was used not only because it is a more sensitive measure than categorical decisions, but also because recently developed algorithms rely on slight differences in similarity ratings [[4], [5], [6], [7]]; among others). It is unclear to what extent humans can assess similarity on a scale of 0–100 rather than reach categorical decisions of “identification”, “elimination”, or “inconclusive”.

Furthermore, it is also important to examine performance on difficult vs. easy cases. Sometimes true matches may look relatively dissimilar while true non-matches look relative similar, which makes some cases more difficult. Decisions should be easier when true matches look similar, and true non-matches look dissimilar. A machine learning algorithm was used to obtain similarity scores for pairs of cartridge case 2D images. The knowledge of which pairs were truly a match or a non-match (the ‘ground truth'), and the similarity information from the algorithm, allowed for splitting the pairs up into easy and difficult groups.

1.1. Background

Pattern-matching forensic methods can be subjective or objective. A subjective method is one in which key procedures involve significant human judgment and discretion, and an objective method is a procedure that is standardized and can be performed by either an automated system or human examiners exercising little or no judgment as it relies on objective quantifiable measurements [8].

The foundational validity of firearms analysis has been questioned [[8], [9]]. PCAST has suggested two directions to strengthen the scientific underpinnings of the discipline: the first is to perform black-box studies to determine error rates in the way firearm comparisons are currently performed, and the second is to develop and test image analysis algorithms for comparing the similarity of tool marks on bullets.

PCAST's guidance about the two directions are being followed by researchers. In the spirit of the first direction, recent black-box studies have found a false positive rate of about 2% in comparisons [10] – although estimates like these have recently come into question because of their treatment of “inconclusives” [[11], [12], [13]]. Following PCAST's second direction, new algorithms (e.g. Refs. [4,14], have been proposed to improve the accuracy of the classification decisions.

However, it is not clear how these two directions relate to one another i.e., how to optimize the division and collaboration between human and machine so they best complement each other (e.g., Ref. [2]. For example, PCAST gives no clear guidance on when algorithms should replace human examiners altogether, and when certain parts of the analysis should be performed by machine algorithms. PCAST only makes it clear that to strengthen pattern-matching disciplines, “Objective methods are, in general, preferable to subjective methods” (page 47).

The push for developing more objective methods and machine algorithms for forensic disciplines has been fueled by the susceptibility of expert decisions to noise and bias, and lack in transparency [15,16]. The 2009 NAS report recommends making “scientific investigations as objective as possible so the results do not depend on the investigator,” and the 2016 PCAST report states that to strengthen the scientific underpinnings of the discipline we should “convert firearms analysis from a subjective method to an objective method.” [8] Recent research has even shown that an algorithm outperforms trained human examiners when evaluating the same samples, specifically in that the algorithm does not have the same problems with inconclusive results as firearm examiners [17].

But subjective methods do have strengths (e.g., [18,19]). There is evidence that humans perform better than algorithms in a variety of tasks [20]. Researchers found that some forensic algorithm methods can be improved: “In specific instances where the algorithm had difficulty in assessing a particular comparison pair, results obtained during the collaborative study with professional examiners suggest ways in which algorithm performance may be improved” [6] ([21,22]; and [23] also research this area). While they do not directly compare algorithms to human examiners, they do discuss how the algorithms perform on the same proficiency tests examiners take and discuss how algorithms can be integrated into the field. Furthermore, forensic examiners learn a wealth of information about class characteristics, such as what type of firearm or ammunition was used.

A hybrid approach of ‘distributed cognition’ [2] in which some parts of the analysis are carried out by human examiners and some by the algorithm, in a collaborative and complementing fashion could utilize the best of both perspectives. This can only be achieved with better understanding of the relative strengths and weaknesses of the human and machine. It is thus important to study which parts of the analysis humans outperform algorithms, and vice versa. This will allow a knowledge-based hybrid process to be developed. Its performance should be compared to the examiner-only and algorithm-only approaches to see if it is better. Note that even if we replace subjective methods altogether, we still want to know why they should be replaced. Not just that they have higher error rates according to a black box study or compared to an algorithm. This type of evaluation will tell us about more specific strengths and weaknesses of the different methods. As new algorithms are developed, this process should be repeated to ensure that the best method, or combination of methods, is used.

In what follows, there is a brief review of the research in psychology, forensic science, and firearm analysis. This literature presents the main arguments regarding the importance of understanding the similarity judgments made by humans and their relationship to those made by machine algorithms. Next, the image dataset, the machine learning algorithm, and the similarity rating results are described.

1.2. Cognitive science issues in firearm analysis

The concept of similarity has been studied for decades (e.g., [[24], [25], [26], [27], [28], [29]].). Making similarity judgments underpins many cognitive processes and plays a major role in learning and making decisions in naturalistic complex tasks [20]. Particularly interesting and important are similarity judgments used by experts in domains that do not have an objective and quantifiable decision thresholds, where experts often have to rely on subjective similarity judgments. For example, many forensic science domains rely on making a subjective judgment of whether two patterns are “similar enough” to conclude that they both come from the same source [[8], [9], [30]].

There has not been a unified method to assess the difficulty or complexity of a comparison. Examiners might consider a comparison complex or difficult, but this is subjective rather than based on data or empirical studies. Researchers have found that, in fingerprints, the quality of a latent print (and thus the difficulty of comparing it to other prints) is usually assessed qualitatively and subjectively by the examiner. There are scales based on points that evaluate the amount of contrast and clarity of features (see [31]; Section 2). Assessing the difficulty of a comparison is challenging because it depends on the stimuli itself and the person doing the comparison, and their interaction, for example, the great variability in the quality of the samples, the examiners' capabilities, and the procedures used in the agencies [32]. We propose to operationalize the difficulty of a comparison using the similarity between two prints as determined by a machine algorithm and relative to whether they were actually matches or non-matches (i.e., similar matches and dissimilar non-matches are classified as ‘easy’, whereas relative similar non-matches and relative non-similar matches are classified as ‘difficult’).

In forensic science evidence found in the crime scene is sometimes compared to the known pattern of the suspect. This can be a pattern of handwriting, fiber, or marks left by teeth, shoe, or tire marks. Even the most used forensic domain, fingerprinting, requires that human analysts compare a latent print from the crime scene with a fingerprint of the suspect. These two patterns are compared, and the human examiner subjectively decides if they are “sufficiently similar” to conclude that they come from the same source (i.e., they are a “match”). Even DNA mixture interpretation requires subjective judgments [33]. Furthermore, even the more objective forensic domains, such as toxicology and drug analysis, require subjective decisions [16]. Hence, the ability to make accurate subjective judgments underpins many of the forensic decision making. In the widely used forensic domain of firearms identification, there has been very little research to explain how such similarity judgments are made.

There are two important research issues we address in the study reported here. First, forensic science and other disciplines must be better informed regarding the ability of humans to make similarity judgments. We need to understand how humans make judgments in forensic firearm identification, and how these may vary by the difficulty. The questions that we aim to address our study are how well humans can make similarity judgments in difficult firearm cases, and how much expertise is needed to make such judgments (i.e., can novices with no knowledge of firearm analysis make such judgments accurately?).

The second issue pertains to the use of computerized systems. This is critical, as it can determine if and to what extent machine learning algorithms are able to do forensic firearm identification in the absence of human intervention, and how best can they work in collaboration with humans. In the context of text documents, examined similarity assessments of machine algorithms vs. humans found that the algorithms (n-grams and latent semantic analysis or LSA) did not perform as well as humans [34]. In fingerprint identifications, AFIS (Automated Fingerprint Identification Systems) are widely used in combination with human conclusions. AFIS systems require the human to mark minutiae in the print, and submit their results to the algorithm, which then provides a list of the most similar matches to the submission. Fingerprint algorithms' ability to work with human examiners has been researched, examining when they can support the human by offloading some of the initial search of databases onto the algorithms, when they can collaborate and distribute cognition as partners, and when the algorithms can take over and replace the human [2]. Of course, the quality of the algorithm matters with regards to whether a human can outperform the algorithm. A high-quality algorithm is more likely to outperform a human than a low-quality algorithm, and the quality can be defined in different ways. Nevertheless, given some high-quality algorithm it is important to know whether a human could outperform it. This type of research and analysis has yet to be conducted in the firearms domain.

2. Image dataset

The bullet casing images of the breech faces collected and analyzed in [35]; shown in Fig. 1, are used. The image dataset consists of images of cartridge breechfaces, from 12 firearms of 3 different types (Ruger P95D, Smith & Wesson 9VE, and Sig Sauer P226 pistols), with 3 different types of ammunition (PMC, Remington and Winchester), and 3 iterations each, for a total of 108 images. The casings were re-imaged by the National Institute of Standards and Technology (NIST), and the data were made available as part of the Ballistics Toolmark Research Database, an open-access research database of fired bullet and cartridge reference data. These images are referred to as the NIST Ballistics Imaging Database Evaluation (NBIDE) dataset.2 Every pair of images was compared by the algorithm [4], to produce a total of 11,556 comparisons. This is twice 5778 (which is 108 choose 2, or in other words, these are all the pairwise comparisons with none repeated between pairs) because the algorithm gives different results if you compare A to B and B to A. The Tai and Eddy's algorithm produces small differences when comparing A to B vs. B to A because one image is aligned to match the other in the comparison, for example for A-B, B is rotated to match A, and for B-A, A is rotated to match B, and the results of the correlation between A and B are not identical between the two orders. However, the differences between the two correlations are very small, between 0.0001 and 0.001. So we selected only the A to B comparisons for our analysis.

Fig. 1.

Low-resolution representation of the NBIDE dataset from a 2007 NIST study of breechface images.

3. Similarity algorithm

This project uses the algorithm written by Tai and Eddy [4]; which was inspired by an algorithm written by the National Institute of Standards and Technology (NIST). NIST created an algorithm to provide a similarity score for a pair of breech face images, but this algorithm is not publicly available. Research groups have attempted to develop similar algorithms that can serve for evaluation and development of decision support tools for firearm analysts. For example, a research group at Michigan State University [14], implemented an algorithm that was not identical to the one written by NIST, but it was “the authors' best guess about what the algo-rithm does based on descriptions written by NIST” [35]. [4] obtained the code from [14] and modified it to improve it in several ways described below.

The measure of similarity produced by Tai and Eddy's algorithm is the maximum cross-correlation function (CCFmax). This algorithm performed all possible pairwise comparisons in the NBIDE dataset, which resulted in 107 × 108 or 11,556 pairwise comparisons. For each pairwise comparison, the algorithm computed a similarity score and the probability of obtaining a higher score by chance.

To perform a pairwise comparison Tai and Eddy's algorithm performs the following activities. 1) Automatically selects breech face marks by finding the cartridge primer region and removing it from the firing pin impression by applying a Gaussian filter and then using a Canny edge detector. 2) Levels the image by fitting a plane and taking the residuals, which enables that the resulting image is free from planar differences in brightness in case the cartridge was not level. 3) Removes the circular symmetry, which occurs, for example, when the surface slopes inwards toward the center, and so the center of the image is darker than the edges. Circular symmetry is removed by fitting a model that captures the symmetry, and then taking the residuals, which will be free from circular symmetry. 4) Performs outlier removal and filtering by using a method used by the NIST [35]. 5) Maximizes correlation by translations and rotations by computing a matrix of correlation values, where each entry corresponds to a particular translation and rotation angles 2.5° apart, and then 0.5° apart in the neighborhood of the highest correlation. The maximum correlation between two images is known as the CCFmax. 6) Computes the probability of obtaining a higher score by chance given a known database. Steps 2, 4 and 5 are modified implementations of work by [14,35]. Steps 1, 3, and 6 were added by [4].3

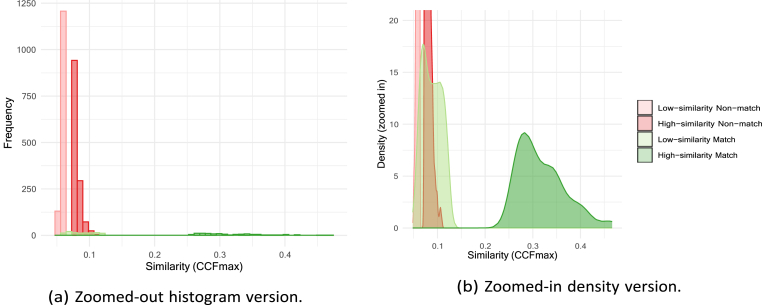
To use an algorithm to determine whether a new pair is a match or a non-match, the algorithm can be trained with experimental data. To do this, the similarity between images is calculated, and the distributions of the similarity measures of known matches and known non-matches, generated by experiments, are calculated, just as in Fig. 2a. Then, the similarity of the new pair is located along the x-axis along the distributions. Using a score-based likelihood ratio approach, if this new value is within the area of the known matches, it is more likely to be a match itself. If it is within the known non-matches, it is more likely to be a non-match. However, if the new pair's similarity is in an overlap region or in a gap between the two distributions along the x-axis, then it is unclear whether it is a match or a non-match. The score-based likelihood ratio gives information about how likely it is that a pair belongs to one distribution vs. another by assessing the heights of the distribution at a point, but the overlap regions leads to less certain conclusions, especially where the distributions have similar heights.

Fig. 2.

Algorithm results from Ref. [4] assessing similarity between pairs of breech-face images. The overlap of the known matches and non-matches motivates our research about whether humans can distinguish between the two categories in this similarity regime.

Fig. 2 shows the distributions of the CCFmax for the match and non-match pairs resulting from the Tai and Eddy's algorithm. The non-match similarity scores distribution has a lower mean and standard deviation (mean = 0.14, sd = 0.008) than the distribution for matches (mean = 0.4, sd = 0.06). And an independent sample Kruskal-Wallis test shows a significant difference across conditions (p = 0.0003). However, there is some overlap between the two distributions, shown in Fig. 2b, suggesting that some pairs that are true matches are graded as having low similarity by the algorithm. In other words, the algorithm is particularly inaccurate in distinguishing pairs that match and pairs that do not match when their similarity is low.

This overlap motivates this study's behavioral research question of whether individuals without training in firearm analysis would be able to distinguish between these two difficult groups of image pairs. That is, would humans be able to judge that matches rated as dissimilar by the algorithm are similar? Although further research could help reduce the overlap, there is often an overlap with such algorithms so it is important to evaluate the performance of human versus machine in the overlap area. Note that our reason for selecting novices instead of examiners was that this research studies the abilities of humans to assess similarity between images, and how they compare to an algorithm.

To study whether humans could distinguish between matches and non-matches in the overlap area, the data was separated into four groups (see Fig. 3): high-similarity matches (HM), low-similarity matches (LM), high-similarity non-matches (HN), and low-similarity non-matches (LN). Within the matches, HM are 75–100% and LM are 0–25% of the distribution. Within the non-matches, HN is 75–100% and LN is 0–25% of the distribution. Avoiding the values at the boundaries (i.e., 26–74%) gives the most extreme pairs, which makes the distinctions between groups clearer.

Fig. 3.

Algorithm results from Ref. [4] (same as Fig. 2, split up into four groups (the top and bottom quartiles of the known match and known non-match distributions). Our research question is whether humans can distinguish between the high-similarity non-matches (bright red) and the low-similarity matches (light green), which overlap. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

The distributions of the two extreme groups (HM and LM) do not overlap, but those of the other two groups do (LM and HN). Also, the standard deviations of the non-match groups are much smaller than for the match groups. These were sampled to have equal numbers of items for each study group.

4. Experiment 1: human similarity judgments in overlap region

The first question of interest was whether human respondents would be able to distinguish between the two overlapping cases, the least similar matches (LM) and the most similar non-matches (HN). To answer this question, a study including only images from the LM and HN groups was performed.

4.1. Participants

One hundred and twenty participants were recruited from Amazon Mechanical Turk (50 were female and 70 were male). On average, the participants were between 31 and 35 years old, and had some years of college (with the mode being a 4-year college degree). On average, the participants spent about 12 min on the study and had a standard deviation of 6.50 min 83 had no visual impairment, and 35 had an impairment with correction. None of the participants were trained as firearm examiners. Ninety two participants did not own a firearm, 26 did, and 2 would rather not say. For the ones who owned a firearm, 6 used it very infrequently, 14 used it once per month, and 6 used it once per year. Thirty one participants had firearm training, 88 did not, and 1 would rather not say. The participants were paid $1.50 USD for participating in the study and an additional bonus of $0.50 for finishing it, for a maximum total payment of $2.00 USD.

4.2. Stimuli and procedures

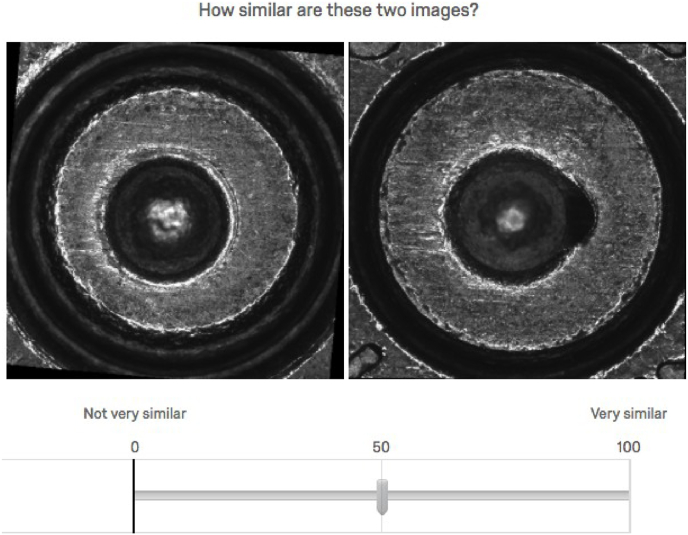
Participants were given instructions, a consent form, and information about their reward for participating and completing the study. For information about the images, they were shown an image of the different parts of the bullet casing (breech face, drag marks, firing pin impression). Then the respondents were asked to judge the similarity for each pair of images on a scale from 0 to 100, as shown in Fig. 4. The slider was set at 50 to start, and the respondents could shift it from “Not very similar” at 0 to “Very similar” at 100. The responses from the first two questions were deleted from the results, since they were considered practice for the respondents.

Fig. 4.

Sample question. The respondent was asked to move the vertical grey marker to a value between 0 and 100 on the line.

A random sample of 10 image pairs was selected from each of the two groups of images in question LM and HN. Fig. 8 in the Appendix shows examples of these. Participants were shown the pairs and asked to assess their similarity. Then, participants were shown the same pairs again in different order to check for consistency, for a total of 20 image-pair judgments. For the purposes of replication, the list of the image labels that were included in the study are shown in Table 6 in the Appendix.

4.3. Results

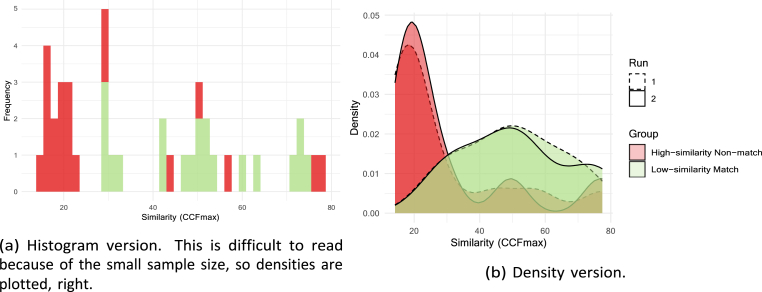
Fig. 5 shows the results from Experiment 1, a histogram on the left and an equivalent density on the right. The histogram is difficult to read because of the small sample size, but it was included here for consistency with the previous figures. Table 1 shows the summary statistics by group.

Fig. 5.

Respondent's results from survey only including two groups.

Table 1.

Experiment 1 summary statistics by group. The values have been averaged over the two runs.

Group	Mean	Median	Std. Deviation
HN	27.6	20	27.2
LM	49.0	52	26.4

The densities of the high-similarity non-matches (HN) and low-similarity matches (LM) mimic the histograms from Fig. 3b, although the respondent's LM have a wider spread farther to the right (i.e., higher similarity) than the corresponding distribution in 3b. There is some overlap between the HN and LM groups, but qualitatively it looks smaller than the overlap in 3b. Finally, there are small peaks in the red non-match distributions at similarity values 50 and 80. Whether the distributions are different from each other must be tested statistically.

An independent samples Kruskal-Wallis test found that these distributions varied significantly across the two experimental conditions (p < 0.01). Mann-Whitney tests found that responses in the LM were significantly higher than those in the HN condition (all p < 0.01). Note that these tests were used because the usual t-test comparison cannot be performed because the distributions are not Normal. Both runs of the study had very similar results, although the second run was slightly higher. The respondents' assessments of similarity of pairs in the LM group are significantly higher than those in the HN group at the 0.05 level. This suggests that the survey responses were not just guesses but instead they represent the respondents' beliefs.

The tests used assume the data are independent. A few of the same images in different groups were included when sampling with replacement. Second, the same respondent answer questions about the four groups (and it is expected that individual respond more similarly to themselves than to others). Third, three comparisons were performed between the groups, which can lead to an increase in the type-1 error. When performing multiple comparisons it is important to adjust the level of the test, with a Bonferroni correction or something similar. The Bonferroni correction sets the level of the test at 0.05/3 = 0.017, and at this level our results are still significant.

A simple linear regression of the respondents' assessed similarity score regressed on the run (1,2), the group (HN, LM), and the respondent ID found that there are significant differences between the different runs, between the different groups, and no significant difference between respondents (see Table 2). The diagnostic plots (QQ plot, stdandardized residuals vs. fitted values, and leverage) showed that the modeling assumptions are satisfied. Informed by these results, the values were averaged over the two runs per respondent, for consistency.

Table 2.

Experiment 1 linear model.

	Dependent variable:
	Reported Similarity (0–100)
Run 2	3.285∗∗∗ (0.739)
Group LM	21.392∗∗∗ (0.736)
Respondent ID	−0.008 (0.011)
Constant	26.571∗∗∗ (0.893)
Observations	5280
R2	0.141
Adjusted R2	0.140
Residual Std. Error	26.753 (df = 5276)
F Statistic	288.067∗∗∗ (df = 3; 5276)

Note: ∗p < 0.1; ∗∗p < 0.05; ∗∗∗p < 0.01.

This experiment provides several pieces of evidence supporting the fact that, on average, un-trained, novice human respondents can distinguish between high-similarity non-matches and low-similarity matches, and thus between matches and non-matches.

5. Experiment 2: human similarity judgments when all conditions are present

It is possible that humans were good at distinguishing between low-similarity matches and high-similarity non-matches because those were the only two types of image pairs that they were presented with. If other types of pairs would have been shown as well, would they have made different decisions about the similarity scores in these two groups? To deal with this potential issue, we ran another study with all four groups of images. This helped us determine whether the respondents could still distinguish between the two middle groups (HN and LM) even when shown the more extreme groups (LN and HM).

5.1. Participants

Experiment 2 was similar to Experiment 1, but with different participants. Our online study had 120 Amazon Mechanical Turk participants, out of which 49 were female and 71 were male. On average, the participants were between 36 and 40 years old, and an educational level of some years of college (with the mode being a 4-year college degree). On average, the participants spent.

18.5 min on the survey and had a standard deviation of about 9 min. Seventy seven participants had no visual impairment, and 43 had an impairment with correction.

None of the participants were trained as a firearm examiner. 88 participants did not own a firearm, 25 did, and 7 would rather not say. For the ones who owned a firearm, 7 used it very infrequently (less than once a year), 12 used it once per month, and 6 used it once per year. Thirty had firearm training, 71 did not, and 4 would rather not say. The participants were paid $3 USD for participating in the study and a bonus of $0.50 for finishing it, for a maximum total payment of $3.50 USD. We ran a small pilot study to make sure the study was running smoothly, and then we ran the large study.

5.2. Stimuli and procedures

As in Experiment 1, 10 pairs of images were selected at random from each of the four groups (Table 6 in the Appendix). The selection of the images and the design of the study was the same as in Experiment 1, except that in this case participants answered a total of 40 questions, 10 in each of the four groups (HM, HN, LM, LN) selected randomly. To clarify, the second experiment had the same exact images as the first, in addition to 20 new images. They did this twice, for a total of 80 questions.

5.3. Results

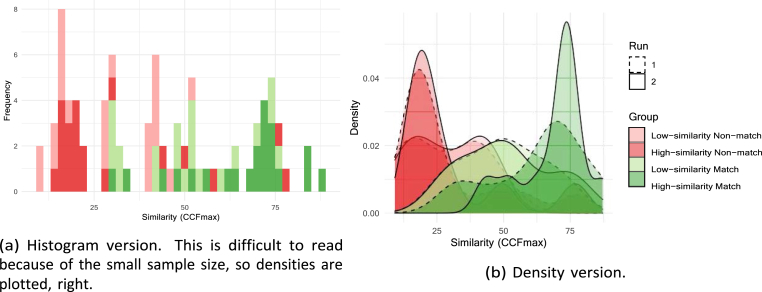
Fig. 6 show the results from Experiment 2, a histogram on the left and an equivalent density on the right displaying the respondents' similarity assessments by group. Table 3 shows the summary statistics by group. It is not immediately clear whether the four densities are separate from each other, or whether the green matches are separate from the red non-matches.

Fig. 6.

Respondent's results from survey including all four groups.

Table 3.

Experiment 2 summary statistics by group. The values have been averaged over the two runs.

Group	Mean	Median	Std. Deviation
HM	65.5	70	26.1
LM	50.3	55	26.3
HN	29.6	21	27.7
LN	28.7	23	24.8

An independent samples Kruskal-Wallis test found that these distributions varied significantly across the four experimental conditions (p < 0.01). Further analysis of pairwise comparisons using the Wilcoxon rank sum test was performed to compare between the group levels, with the Bonferroni correction for multiple testing. This test found the results shown in Table 4, that the only pair of groups that is not statistically significantly different from each other at the 0.05 level is LN-HN (bright red and light red groups). Table 4 shows the pairwise comparison p-values. Finally, as in Experiment 1, both runs of the study had very similar results, although the second run was slightly higher (see Table 5).

Table 4.

p-values of pairwise comparisons using the Wilcoxon rank sum test with Bonferroni correction. The only pair of groups that is not statistically significantly different from each other at the 0.05 level is LN-HN.

	HM	HN	LM
HN	∼ 0	–	–
LM	0.03232	0.00107	–
LN	∼0	1.00000	0.00012

Table 5.

Experiment 2 linear model.

	Dependent variable:
	Reported Similarity (0–100)
Run 2	1.977∗∗∗ (0.524)
Group HN	−35.865∗∗∗ (0.730)
Group LM	−15.104∗∗∗ (0.739)
Group LN	−36.840∗∗∗ (0.721)
Respondent ID	−0.005 (0.007)
Constant	64.964∗∗∗ (0.722)
Observations	10,200
R2	0.261
Adjusted R2	0.260
Residual Std. Error	26.192 (df = 10194)
F Statistic	719.501∗∗∗ (df = 5; 10194)

Note: ∗p < 0.1; ∗∗p < 0.05; ∗∗∗p < 0.01.

As in the first experiment, a simple linear regression was performed. The respondents' assessed similarity score was regressed on the run (1,2), the group (LN, HN, LM, HM), and the respondent ID. The model found that there are significant differences between the different runs, between the different groups, and no significant difference between respondents (see Table 2). The diagnostic plots (QQ plot, stdandardized residuals vs. fitted values, and leverage) showed that the modeling assumptions are satisfied. Informed by these results, the values were averaged over the two runs per respondent, for consistency.

The linear model shows significant differences between the groups, but the nonparametric test shows no difference between LN and HN. Since the distributions of the scores are not normal, it is prudent to rely on the nonparametric test when comparing differences by group. Nevertheless, the model gives information about variability by run and respondent.

This experiment provides evidence that the respondents can discriminate between the matches and non-matches, and specifically between LM and HN, with a p-value less than 0.05.

6. Comparison across experiments and against the algorithm

Experiments 1 and 2 both found that respondents can differentiate between high-similarity non-matches (HN) and low-similarity matches (LM), or in other words, between matches and non-matches (with p < 0.01 in the nonparametric tests). These findings of are robust to including the two easy groups (LN and HM), because there was not much variation in the distributions of LM and HN between the two experiments. Thus, even when the participants observe pairs of images from the HM and LN (“easy”) groups alongside the LM and HN (“difficult”) groups, the results are the same as when they are shown only the LM and HN (“difficult”) groups.

The algorithm categorized the similarity scores for the LM group as overlapping with the scores of the HN group (as shown in Fig. 2b), and thus the algorithm cannot distinguish between matches and non-matches. Instead, the study respondents were able to distinguish between matches and non-matches significantly. Thus, this study finds evidence that the novice human participants outperformed the algorithm in distinguishing between matches and non-matches.

7. Discussion

This study compared the similarity scores of pairs of 2D images of cartridge cases given by a machine algorithm versus those given by untrained humans. Both the algorithm and the humans were asked to give similarity scores from 0 to 100. We were able to divide the pairs into true matches and true non-matches. Using the algorithm's similarity score and the knowledge of whether a pair was a true match or non-match, the pairs were divided into easy (high-similarity matches, low-similarity non-matches) and difficult (low-similarity matches and high-similarity non-matches) categories. This allowed the assessment human performance at different levels of difficulty.

The study found that naive human participants outperformed the algorithm in the sense that they consistently judged matches to be more similar than non-matches, even in the difficult cases (LM, HN). However, within the non-matches, the results were not as clear. The human participants tended to find as much or more similarity in low-similarity non-matches, as in high-similarity non-matches. For reasons that cannot be fully explained by these results, humans seem to be particularly good at detecting differences within relatively similar images and at detecting similarities in quite different images. One aspect that should be further explored is that the algorithm only used limited parts of the image (the breech face) and the humans had access to the entire image, including the firing pin impression. Perhaps including all the information to train the algorithm could improve the performance of the algorithm. This might be an interesting result in psychology, and it is different than how one would program an automated algorithm. Thus, it is worth further investigation.

While the results comparing differences between human and machine algorithmic decision-making are interesting in their own right, they also have potentially important policy implications. In general, a collaborative method that utilizes the strengths of both subjective human decisions and objective algorithmic decisions, while avoiding their weaknesses, may be preferable to strict human-only or algorithm-only approaches. Rather than competing for supremacy, a hybrid collaborative approach seems best. However, the best way to combine them is a topic for further important research.

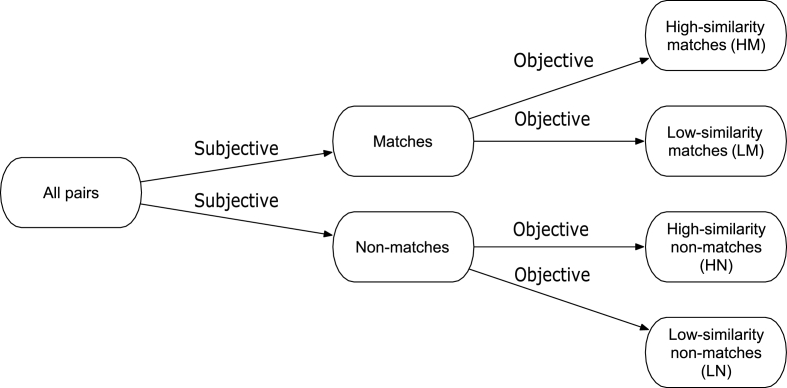
For instance, using only the results from this study, may suggest that applying a subjective method to distinguish between “identification” and “exclusion” and then employing an objective method to distinguish between high- and low-similarity cases within each subgroup maybe optimal. This approach is shown in Fig. 7. In contrast, our study suggest that using the algorithm first to distinguish between “identification” and “exclusion” and then using a subjective method to distinguish between high- and low-similarity pairs in each group would be less accurate than using an objective or subjective method alone. As the data reflects, untrained humans are relatively good at correctly distinguishing between matches and non-matches, but not as good at assessing similarity within the matches and the non-matches. In contrast, the Tai and Eddy [4] algorithm distinguishes some of the matches from the non-matches, but not all.

Fig. 7.

Decision tree for the optimal decision-making according to our study results. This does not generalize to all firearm comparisons, but shows the results from our experiment. It illustrates the importance of combining subjective and objective decision-making processes in the order determined by empirical analysis.

Given that this is the first research to make such comparisons, of course, one must be careful in generalizing these results to other forensic comparison domains, or even to all firearms analysis. This is because, for example, firearm examiners are trained, other disciplines differ from bullet casing examination, and the results might be different with other algorithms. These results suggest that the hybrid approach used in fingerprint algorithms, like AFIS, might be more accurate than either only human or only machine approaches.

This could be the first in a series of studies to compare humans and machines in forensics. For instance, the reason for selecting novices instead of examiners was that this research studies the abilities of humans to assess similarity between images, and how they compare to an algorithm. A second study could be performed to compare how trained firearms examiners perform in comparison to the novices, and this would answer how training affects the human vs. machine comparison. Other studies could compare trained examiners to different types of algorithms, and evaluate hybrid approaches.

These results suggest that it would be a mistake to pick between either human or machine firearms comparison approaches. Instead, methods and approaches should be evaluated, and hybrid, combined collaborative approaches considered. Hybrid here means distributed cognition, whereby the human has an important role and actually makes some key decisions and contributions. However, the process by which human and machine are combined will need to be determined by further empirical research, for specific algorithms, disciplines, human expertise, and for the various stages in the comparison.

Declaration of competing interest

The authors do not have any conflict of interest to report.

Appendix.

Table 6.

NBIDE numerical labels of the pairs of images that were randomly selected from each of the four groups. The first entry under HM, 025,100, represents the pair of images NBIDE025 and NBIDE100. Recall that HM = high-similarity match, LM = low-similarity match, HN = high-similarity non-match, LN = low-similarity non-match. See Section 2 for more information about how the groups were created.

HM		LM		HN		LN
025	100	032	079	017	043	036	090
022	055	006	127	034	142	006	035
091	100	029	112	010	027	041	128
130	138	030	040	090	092	023	055
118	134	063	084	060	134	127	136
078	102	042	056	060	090	097	102
054	075	023	079	017	029	007	040
022	096	032	066	008	117	023	051
053	120	023	061	078	119	049	119
055	096	032	128	060	110	031	057
053	067	027	062	015	100	051	103

Table 6 shows the labels of the images that were randomly selected from each group to be included in the experiment. This list can be used to replicate the experiment.

Fig. 8.

Sample pairs of images from each of the four groups. The pairs are organized from most similar to least similar from left to right, according to the Tai and Eddy's algorithm, with no particular order from top to bottom.