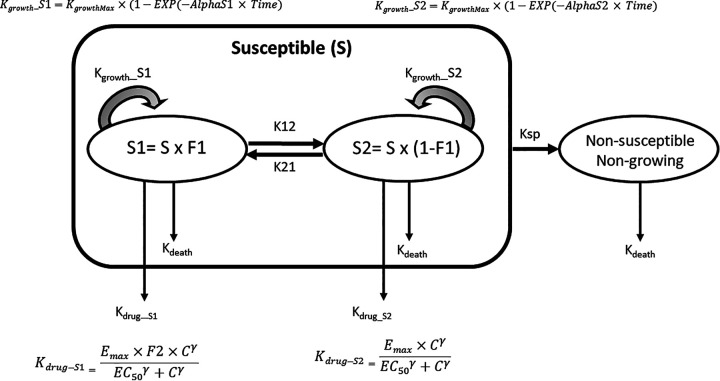
FIG 3.
PK/PD model for colistin time-kill analysis. All bacteria were assumed to be in a susceptible (S) growing population from initial inoculation, with transfer to a nongrowing and nonsusceptible population. The starting susceptible bacterial population was considered to be heterogenous with two subpopulations, representing a dominant population of highly susceptible bacteria (S1) and a small population of less susceptible bacteria (S2) with a dynamic equilibrium between the two subpopulations driven by first-order rate constants of K12 and K21. The same maximal growth rate (Kgrowth) was considered for S1 and S2, but the rate to achieve this maximal growth rate (alpha) was different for S1 and S2 (AlphaS1 for S1 and AlphaS2 for S2). The system was considered to be already in equilibrium during the initial exposure to colistin, and it is the K12/K21 ratio that was estimated by directly evaluating a distribution factor (F1) of the population between the population S1 (F1) and subpopulation S2 (1 − F1) with F1 = 1 − (K12/K21). The irreversible transfer rates to a nongrowing state (KSP) were considered identical for S1 and S2 All bacteria were subject to a constant rate of natural cell death (Kdeath) fixed to 0.17 h−1. The effect of colistin (Kdrug), having the same dimension as Kdeath (h−1), was described by a Hill model with three parameters (Emax for efficacy, EC50 for potency, and gamma for the slope), with C being the colistin concentration at which bacteria are exposed. Kdrug was considered additive to the natural cell death, with a potentiation factor (F2) for the highly susceptible subpopulation S1. F2 increases Kdrug by only increasing Emax because in a preliminary analysis, it was shown there was no difference in EC50s for the two S1 and S2 subpopulations. A model script is given at https://rvc-repository.worktribe.com/output/1567805/supplementary-data-quantitative-pharmacodynamic-characterization-of-resistance-vs-heteroresistance-of-colistin-in-e-coli-using-a-semi-mechanistic-modelling-of-killing-curves.