Emergence of synchronized multicellular mechanosensing from spatiotemporal integration of heterogeneous single-cell information transfer

Summary

Multicellular synchronization is a ubiquitous phenomenon in living systems. However, how noisy and heterogeneous behaviors of individual cells are integrated across a population toward multicellular synchronization is unclear. Here we study the process of multicellular calcium synchronization of endothelial cell monolayer in response to mechanical stimuli. We applied information-theory to quantify the asymmetric information-transfer between pairs of cells and defined quantitative measures to how single cells receive or transmit information within a multicellular network. Our analysis revealed that multicellular synchronization was established by gradual enhancement of information spread from the single cell to the multicellular scale. Synchronization was associated with heterogeneity in the cells’ communication properties, reinforcement of the cells’ state and information flow. Altogether, we suggest a phenomenological model where cells gradually learn their local environment, adjust and reinforce their internal state to stabilize the multicellular network architecture to support information flow from local to global scales toward multicellular synchronization. A record of this paper’s Transparent Peer Review process is included in the Supplemental Information.

Graphical Abstract

eTOC Blurb

We quantitatively characterized the process of mechanically stimulated multicellular calcium synchronization. By applying Granger-causality and network analysis to live movies, we revealed that increased connectivity, heterogeneity, and memory, at the cellular scale, facilitated the emergence of synchronization across a multicellular network by gradual transition from local to global information spread.

Introduction

Synchronized multicellular dynamics is the basis of many critical physiological processes, such as the rhythmic beating of cardiomyocytes, planar cell polarity, and brain activities. The human endothelium, for instance, consists of a staggering over one trillion endothelial cells which constantly monitor environmental cues such as shear stress, in order to collectively regulate the vasculature tone (Davies, 2009; Wolinsky, 1980). However, a fundamental question remains elusive: how synchronization in the group emerges from the interactions of individual cells, each making stochastic decisions based on noisy cues from their local environment?

A major challenge toward establishing multicellular synchronization lays at how single cells translate environment information to intracellular signaling responses (Perkins and Swain, 2009). Signaling in cells often rely on low copy numbers of proteins (Huang et al., 2007) and diffusion limited intracellular transport (Brangwynne et al., 2009). These effects, often considered as intrinsic noises, lead to variable single cell signaling dynamics even in response to identical external stimuli (Elowitz et al., 2002; Swain et al., 2002). Cell-to-cell variation, or intercellular heterogeneity, is present even for cells originating from the same genetic background, also complicates our understanding of multicellular synchronization processes. Such cell-to-cell variation, or non-genetic intercellular heterogeneity, may arise from differences in gene expression levels (also terms as extrinsic noise), alternative splicing, as well as post translation modifications (Bintu et al., 2016; Elowitz et al., 2002; Gut et al., 2018; Ng et al., 2018; Raj and van Oudenaarden, 2008). Intercellular heterogeneity implies that individual cells take different states, or phenotypes, which may be related with intrinsic noises such as by varying the copy number of receptors to modulate the probability of activation (Young et al., 2008). Intercellular heterogeneity also modulates the propensity of cells to interact with their peers, as the communication between cells depend on specialized molecular channels such as gap junctions (Calderón and Retamal, 2016; Nicholson and Bruzzone, 1997). However, it is not known whether non-genetic intercellular heterogeneity can play a constructive role in information transfer between cells in multicellular systems. As such, we ask whether some cells within a group function as leaders or followers, promoting the spread of information through the group, while others act individually, and whether such heterogeneity is important for the synchronization of multicellular dynamics.

Previously, we demonstrated that cell-cell communication through gap junctions (Fujii et al., 2017) modulated ATP-induced calcium signaling in monolayers of fibroblast cells (Sun et al., 2012). Tuning the levels of intercellular communications, by varying cell densities, inserting weakly-communicating cells, and by pharmacologically inhibiting gap junctions, controlled the temporal coordination of calcium signaling in neighboring cells (Potter et al., 2016; Sun et al., 2012). Others have also highlighted the role of local gap-junction mediated cell-cell communication in functional multicellular connectivity of neural progenitor cells at the vascular interface (Lacar et al., 2011), in neural stem cell reactivation in the blood-brain barrier (Spéder and Brand, 2014), in neural progenitors cell proliferation during embryonic development (Malmersjö et al., 2013) and in coordinated fate decisions (Ho et al., 2021).

To elucidate how information transfer between single cells is integrated to synchronize population-level cellular responses, we study the physiological process where monolayers of endothelial cells collectively sense and respond to external shear stress. Endothelial cells line the interior surface of blood vessels and form a monolayer that experiences varying levels of shear stress from blood flow (Hill et al., 2010; Yin et al., 2007). Upon changing the flow rate (e.g., during acute wound), endothelial cells detect the change in shear stress, inform other cells such as smooth muscle cells, and adjust their internal signaling accordingly. Central to the cascade of events, shear stress leads to downstream ATP activation which modulates calcium signaling at the subcellular scale (Faehling et al., 2002; Kohn et al., 1995; Rubanyi and Vanhoutte, 1988). As a group, the endothelial cells must coordinate their signaling dynamics to achieve a coherent and collective response. Specifically, intercellular calcium levels are synchronized via gap junction-mediated cell-cell communication (Kumar and Gilula, 1996; Sun et al., 2012). Such synchronized calcium signaling is instrumental in modulating reepithelialization, angiogenesis, and extracellular matrix remodeling, which are essential processes in wound repair (Aihara et al., 2013; Eming et al., 2014; Handly and Wollman, 2017; Lee et al., 2019; Shannon et al., 2017).

In this study we developed an integrated experimental-computational approach to quantitatively evaluate the roles that single cells take during the emergence of multicellular synchronization. Using this platform, we identified three key functions whereby single cells contribute to collective information processing that ultimately leads to multicellular synchronization. Division of labor, where single cells take differentiated functional roles in collective information processing; Cell memory, where single cells maintain and reinforce their specified functional roles in cell-cell communication in response to repeated external stimuli; And information flow, where the information gradually propagates spatially from the scale of single cells to eventually synchronize the collective.

Results

Endothelial cells in a monolayer adapt their calcium dynamics in response to external shear stress

We employed a microfluidics system that can precisely control the temporal profile of the shear stress that the cells experience (Fig. 1A top). We grew confluent monolayers of HUVEC (Human Umbilical Vascular Endothelial Cell) cells on the bottom surface of the flow channels (Fig. 1A bottom). A computer interfaced flow switch regulated input pressure to induce smooth flow profiles in the microfluidic channel as verified by particle image velocimetry (Fig. 1B). The shear stress -induced calcium signal of the HUVEC cells was imaged with the fluorescent calcium indicator Calbryte-520 at single cell resolution (Fig. 1A inset, Video S1). We manually marked each cell center (Fig. 1A inset), recorded the intracellular calcium signal as a time-series of fluorescent intensity for every cell and verified that the magnitude of the cell’s calcium signal correlated with the magnitude of the applied flow shear stress (Fig. 1C, Methods). This setting enabled us to investigate the collective mechanosensing of HUVEC cells to fluid shear stresses, a scenario that mimics the physiological function of the endothelium.

Figure 1. Collective calcium signaling of mechanosensing as a model to investigate the emergence of multicellular synchronization at the single cell resolution.

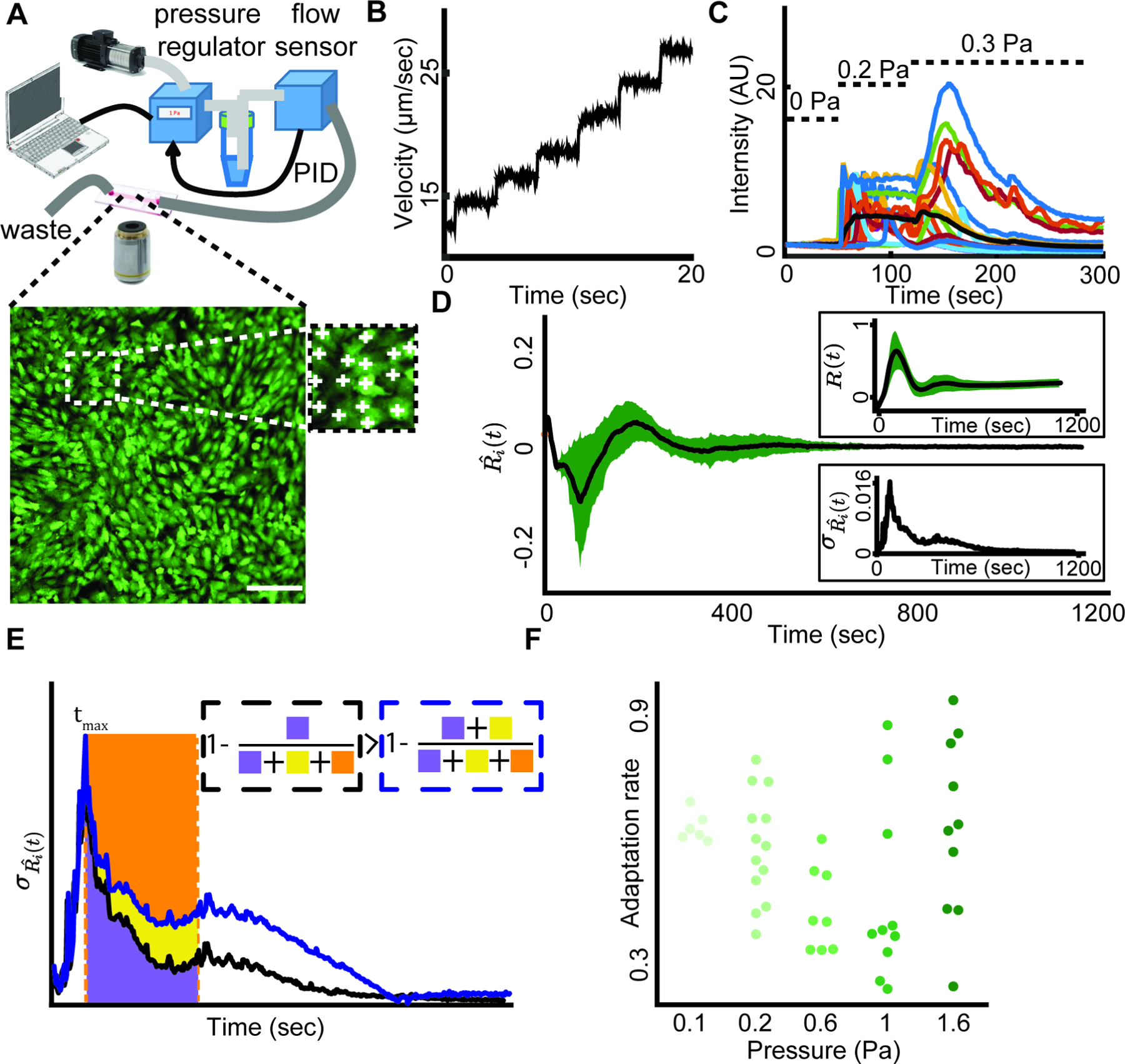
(A) In a typical experiment, a monolayer of HUVEC was cultured in a microfluidic device where fluid flow applied shear stress on the cells. Top: Schematics of the setup. The input pressure that drives a laminar flow in the single channel microfluidics is controlled by a computer interface. The pressure is regulated in real time via a PID loop consisting of a pressure regulator and a flow sensor. Bottom: A monolayer of HUVEC loaded with the fluorescent calcium indicator Calbryte-520 as a readout of the cellular response to flow shear stress. Scale bar = 50 μm. Inset: manual annotation of single cells.

(B) Particle image velocimetry verified that the regulated input pressure produces a smooth flow profile in the microfluidics channel.

(C) Cells respond to step increase in the flow shear stress. Relative intensity is the relative change of the fluorescence intensity from the basal cell level (Methods). Colored lines: individual cell calcium responses. Black line: mean response of over 400 cells in the field of view. Dashed horizontal lines indicate the time interval of 0, 0.2, 0.3 Pa shear stress correspondingly.

(D) Multicellular calcium dynamics is synchronized over time in response to external mechanical stimuli. The flow shear stress is applied from the onset of imaging (t = 0). The calcium dynamics of each cell was represented by the time-derivative of its relative fluorescent intensity. Black: mean calcium Ri(t) dynamics; Green: standard deviation. Top inset: mean (black) and standard deviation (green) of single cell calcium relative intensity (Methods) over time. Bottom Inset: standard deviation of calcium dynamics over time.

(E) Depiction of the adaption rate measure overlayed on the plot of the standard deviation of calcium dynamics overtime. There are two solid lines; the black represents faster adaptation compared to blue. Adaption rate of the black / blue solid line is one minus the ratio between the area under the curve for 400 seconds (200 frames, purple / yellow + purple area) and the area of the rectangle whose height is set by the maximum variations of individual cell dynamics (yellow + orange + purple area). See Methods for full description.

(F) Multicellular adaption rate for increasing shear stress levels. Each observation represents a biological replica. N =47 biological replicates: n = 6 (0.1 Pa), n = 13 (0.2 Pa), n = 8 (0.6 Pa), n = 10 (1 Pa), n = 10 (1.6 Pa).

Upon exposing the cells to a step-like increase in shear stress to 0.2 Pa, which is similar to those that an endothelial cell experiences during acute bleeding (Albuquerque et al., 2000), the variability in the cells’ temporal derivative of their calcium signal (termed calcium dynamics, annotated ${\widehat{R}}_l\left(t\right)$ (Methods)) increased and then gradually reduced until the cells adapted to the external stress and converged to a steady state (Fig. 1D). We defined the adaptation rate as $1-\left(\frac{{\int }_{t_{max}}^{t_{max}+400}{\sigma }_{\widehat{R_l}\left(t\right)}\left(t\right)}{40\ast {\sigma }_{\widehat{R_l}\left(t_{max}\right)}}\right)$, where ${\sigma }_{\widehat{R_l}\left(t\right)}\left(t\right)$ is the population-level standard deviation of single cell calcium dynamics ${\widehat{R}}_l\left(t\right)$ at time t, and $t_{max}=\underset{t}{argmax}{\sigma }_{\widehat{R_l}\left(t\right)}\left(t\right)$ is the time of the peak variability in calcium dynamics (Methods, Fig. 1E). The adaptation rate is a non-parametric measurement for the speed that the multicellular system adapts to the external stress. When a system rapidly synchronizes, adaptation rate approaches one. Conversely, if a system maintains a large deviation between the dynamics of individual cells, adaptation rate is close to zero. In general, higher adaptation rate implies faster multicellular adaptation to the external stress (Fig. 1E black curve adapts faster than blue curve). The endothelial monolayer adapted to increasing levels of shear stress ranging from 0.1 to 1.6 Pa (Fig. 1F, Fig. S1 - parametric exponential model) demonstrating the robustness of the multicellular system in adaptation to varying physiological-relevant levels of external mechanical stimuli (Charbonier et al., 2019). Altogether, these results suggested that the cells gradually adapted despite the vast variability in single cell calcium response at the onset of shear stress.

The interplay between information flow, heterogeneity and multicellular adaptation

We hypothesized that integrating and propagating information from the local scale, between single cells, to the global scale, drove the adaptation of an inherently heterogeneous multicellular system to external mechanical stimuli. To investigate this hypothesis, we defined quantitative measures for cell-cell communication. If two cells communicate, we expect the past calcium dynamics of one cell to contain information regarding the future calcium dynamics of the other cell. Defined in this way, cell-cell communications can be bidirectional and asymmetric – cell A can influence its neighbor B differently from how cell B influences A (Fig. 2A). To quantify asymmetric cell-cell communication, we used Granger Causality (Granger, 1969) (GC), a classic statistical method from the field of information theory, to infer cause-effect relationships between cell pairs from their fluctuating calcium dynamics. Granger Causality uses linear regression to quantify the extent to which the prediction of values in one time series can be improved by including information from another time series. This provides us with an established framework to extract feedback and feedforward relations from pairwise variables’ fluctuating time-series.

Figure 2. Correlating information flow, collective and local heterogeneity in single cell information transfer and multicellular adaptation.

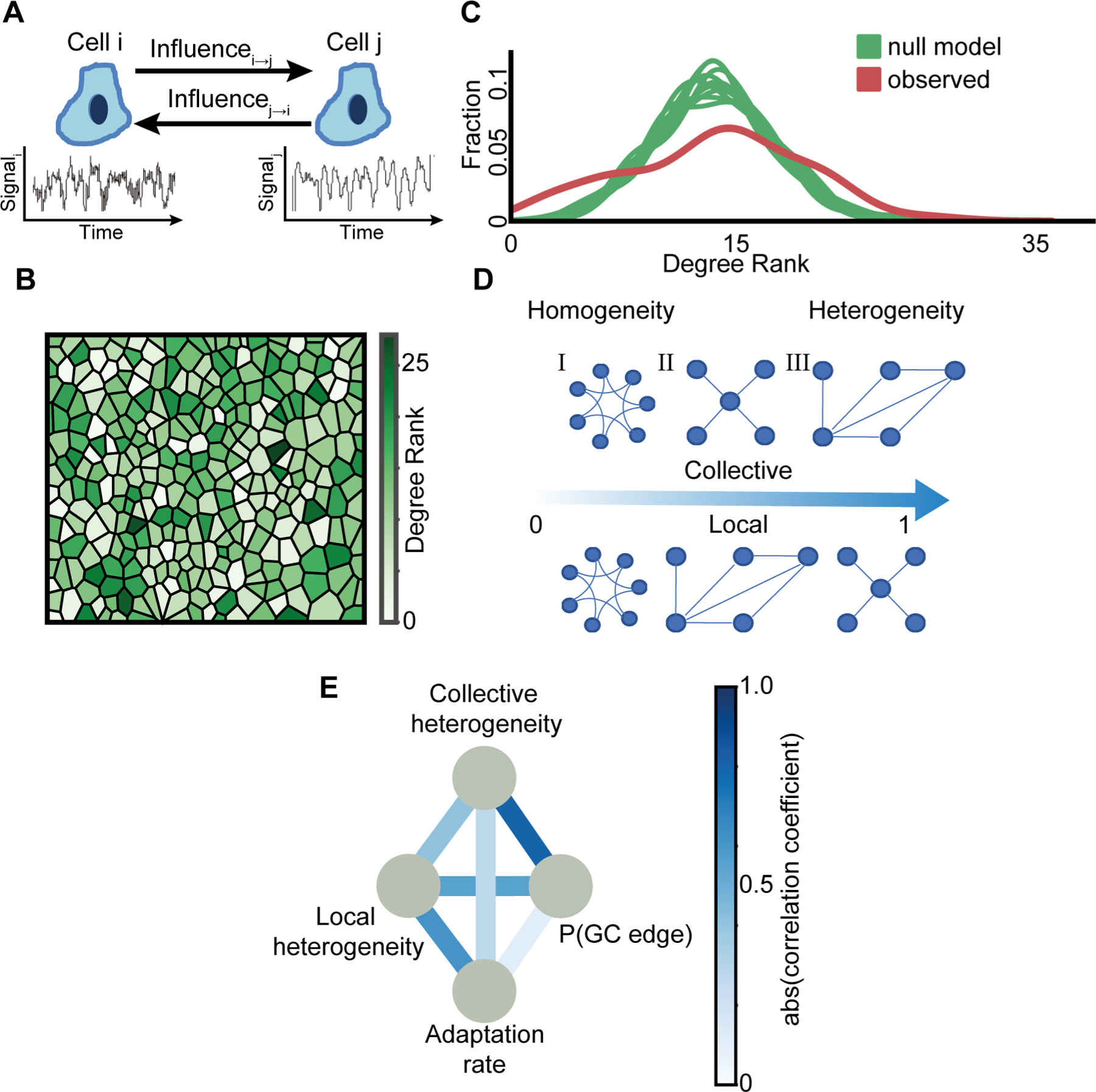
(A) Schematics of cell-cell communication. Generic estimation of the asymmetric mutual influence between a pair of cells from their fluctuating time series. The influence of cell i on cell j is defined as the extent to which the past signal of cell i improves the prediction of cell j’s signal beyond the past signal of j alone and is determined using the pairwise asymmetric Granger Causality statistical test.

(B) Visualization of the spatial single cell heterogeneity of the degree rank (in-degree + out-degree). The color scale is linear.

(C) Heterogeneity in degree rank distribution. The Kernel Density Estimation (KDE) of the degree rank distributions of 10 null models that considered random shuffling of GC edges while preserving the probability for an edge (green) versus the experimentally observed degree rank distribution (red). The raw distribution (input to KDE) is shown in Fig. S3A, with Rinku index ~29 versus ~25 for the observed and null model correspondingly.

(D) Example of collective (top) and local (bottom) heterogeneity for three different network structures. Networks are ordered from left-to-right according to their heterogeneity levels measured with (Jacob et al., 2017) (collective) and (Estrada, 2010) (local). Graph (I) node degree ranks are (2,2,2,2,2,2): local heterogeneity = 0, collective heterogeneity = 0. Graph (II) node degree ranks are (1, 4, 2, 2, 3): local heterogeneity ≈ 0.38, collective heterogeneity ≈ 1. Graph (III) node degree ranks are (1,1,1,1, 4): local heterogeneity = 1, collective heterogeneity ≈ 0.59. See Methods for full details.

(E) Pairwise associations between two heterogeneity measures (local heterogeneity, collective heterogeneity), adaptation rate and GC edge probability. Edges color represents the level of association, as quantified by the magnitude of correlation coefficients. Color scale is linear. Note that some edges reflect positive correlations (e.g., collective heterogeneity - GC edge probability) while others reflect negative correlations (e.g., local heterogeneity – adaptation rate). N = 23 biological replicates, across shear stress levels, that passed the stationarity criterion were considered to calculate correlations. See full data (with signed correlations) in Fig. S4.

To avoid spurious cause-effect relations, Granger Causality requires the time-series being analyzed to be stationary, i.e., fluctuating signals with a consistent mean and variability. Therefore, we excluded experiments where less than 85% of the cells passed two stationary tests (Kwiatkowski–Phillips–Schmidt–Shin (Kwiatkowski et al., 1992) and Augmented Dickey–Fuller (Cheung and Lai, 1995), Fig. S2A, Methods) and in the remaining experiments we analyzed only the cells that passed both stationary tests. When one cell’s calcium dynamics significantly contributed to the accurate prediction of another cell’s signal, we defined a directed GC edge from the first cell to the other (Methods). For every cell in the monolayer, we calculated the degree rank as a measurement for the cell’s involvement in influencing or being influenced-by cells in its local vicinity -- cells with topological distance up to two (nearest neighbor cells and next-to-nearest neighbor cells, Methods, Fig. S2B–C). Cells took different roles in the multicellular communication network as indicated by the spatial heterogeneity in their degree ranks (Fig. 2B), which was higher than a null model that considered random shuffling of GC edges (Fig. 2C, Fig. S3A–B, Methods), and was only associated very weakly with the number of cell neighbors (Fig. S2D).

To quantitatively explore the role of heterogeneity in the cells’ degree rank, we correlated four metrics that characterized adaptation, information flow, collective and local heterogeneity respectively. (1) The adaptation rate measures the dynamics of the multicellular adaptation to external mechanical stimuli (Fig. 1E). (2) The GC edge probability, or P(GC edge), is the probability of a GC edge from all potential edges, a proxy for the overall information flow within the multicellular network. (3) The collective heterogeneity is a measurement for the variability of the cells’ degree ranks (Jacob et al., 2017). The collective heterogeneity is calculated directly from the network’s degree distribution and provides a normalized measure that is independent of the network’s topology and size (Fig. S3B, see Methods for full details). For example, a network in which all the nodes having the same degree is considered as completely homogeneous while a more complex network such as scale-free that has a degree distribution approximates as a power-law (Amaral et al., 2000) is considered a more heterogeneous network (Fig. 2D – top). (4) The local heterogeneity, or the Estrada index, measures the degrees differences between all pairs of communicating cells capturing the heterogeneity in the local network’s structure (Estrada, 2010) (see Methods for full details). The Estrada index is equal to zero for regular networks, where all neighboring cells have the same degree, and equal to one for star graphs (Fig. 2D - bottom). The observed local heterogeneity of all experiments spatially shuffled the cells’ neighbors while preserving the same degree rank (Methods) implying higher local homogeneity (Fig. S3C). Thus, in response to step-like increase in shear stress the multicellular network was characterized by collective heterogeneity and local homogeneity.

We pooled together the 23 experiments across the shear stress range of 0.1–1.6 Pa and correlated the four measurements (Table S1). Collective heterogeneity was correlated with the GC edge probability while the local heterogeneity was negatively associated with the adaptation rate as well as with the GC edge probability. The pairwise correlations are depicted in Fig. 2E and detailed in Fig. S4. Cumulatively, our results suggest a transition from local to global scales in the multicellular network organization. Rapid adaptation is associated with local homogeneity, but has a marginal correlation with the collective heterogeneity. Active information flow is associated with both collective heterogeneity and local homogeneity in communication. The scale-dependent dynamics suggest propagation and integration of information from nearby cells into a decentralized network architecture, a mechanism we further investigate.

Gap-junction mediated multicellular synchronization to periodic mechanical stimuli

After characterizing the communication networks exhibited by endothelial cell monolayers to shear stress, we asked if the network could be trained to adapt to time-dependent external stimuli. To this end, we extended our assay to multiple rounds of repeated mechanical stimuli (Video S2). By treating each round as an independent cycle, and comparing single cell responses across cycles, we could focus on the evolution of synchronization in the multicellular system (Fig. 3A, Methods). We found that the HUVEC monolayer reinforced synchronization as observed by the gradual decrease in the standard deviation of the cells’ calcium dynamics ${\sigma }_{\widehat{R_l}\left(t\right)}\left(t\right)$ (Fig. 3B). To confirm the role of intercellular communication in multicellular synchronization, we inhibited gap junctions or reduced cell density (Methods). In both cases the multicellular network failed to effectively synchronize (Fig. 3C–D, S5A–B).

Figure 3. Information flow and collective heterogeneity are associated with multicellular synchronization to periodic mechanical stimuli.

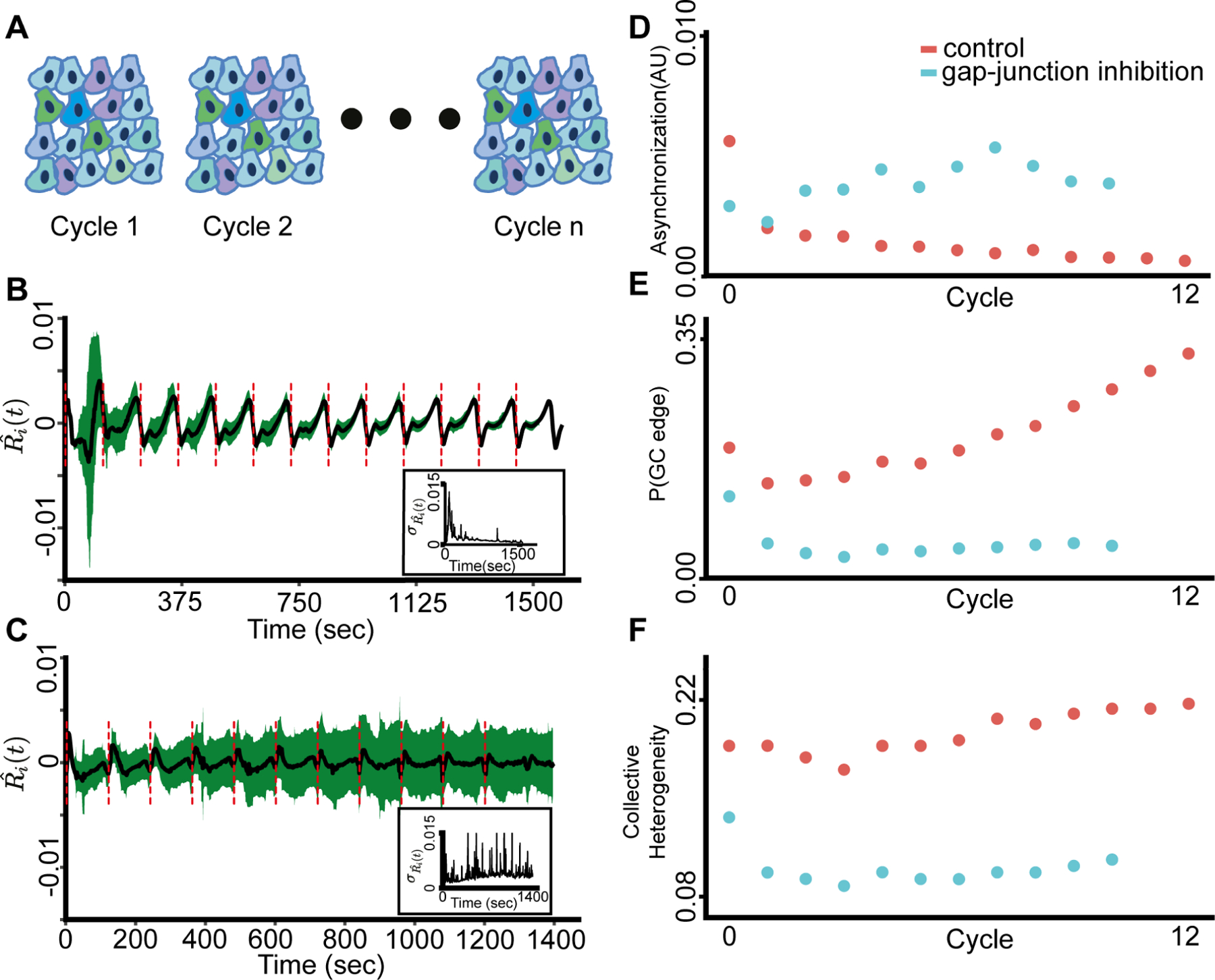
The shear stress was applied from the onset of the experiment (t = 0).

(A) Depiction of the periodic mechanical stimuli experiment setup that included 13 cycles of continuous shear stress in 10 biological replicates (Methods).

(B) Multicellular calcium dynamics is synchronized over time to periodic external mechanical stimuli. In total there are 13 cycles. Black: mean calcium dynamics; Green: standard deviation; Red dashed lines: shear stress onsets. Inset: standard deviation of calcium dynamics over time.

(C) Gap junctions are required for multicellular synchronization. The calcium dynamics fail to synchronize following gap-junction inhibition. Representative of two experiments. Black: mean calcium dynamics; Green: standard deviation; Red dash lines: shear stress onsets. Inset: standard deviation of calcium dynamics over time.

(D) Multicellular calcium dynamics synchronized over time for control (red) (Pearson coefficient = −0.7067, p-value < 0.007) but not for gap-junction inhibited (cyan) monolayers (Pearson coefficient = 0.6442, p-value < 0.0325).

(E) Information flow increased over time for control (red) (Pearson coefficient = 0.9054, p-value < 0.0000207) but not for gap-junction inhibited (cyan) monolayer (Pearson coefficient = −0.3726, p-value < 0.25898).

(F) Collective heterogeneity increased over time for control (red) (Pearson coefficient = 0.8836, p-value < 0.000062) but not for gap-junction inhibited (cyan) monolayer (Pearson coefficient = −0.2376, p-value < 0.4818).

Synchronization coincided with a gradual increase of the information flow, i.e., the cell’s mean GC edge probability (Fig. 3E), and with the collective heterogeneity (Fig. 3F) in intercellular communication. These relations were not measured upon gap-junction inhibition and sparser cell seeding (Fig. 3E–F, Fig. S5C–D, Fig. S6). We did not observe a clear pattern in the local homogeneity measure (Fig. S7). These results, summarized in Table S2, indicate the multicellular network gradually synchronizes to cycles of external mechanical stimuli in a local mechanism that is consistent with jap-junction mediated communication.

Functional cell memory: cells maintain their states in the communication network and reinforce them over time

To characterize the asymmetric communication roles that single cells take during the multicellular synchronization we calculated for each cell the transmission score and the receiver score as measures for being influential or influenced-by cells in its local vicinity (up to topological distance of two). We defined the transmission score as the probability of outgoing GC edges, and the receiver score as the probability of ingoing GC edges (Fig. 4A) (Methods). The observed trend of improved synchronization coincided with a gradual increase of the (population) mean receiver and transmission scores over time (Fig. 4B, Video S3, Video S4).

Figure 4. Functional cell memory is reinforced over time.

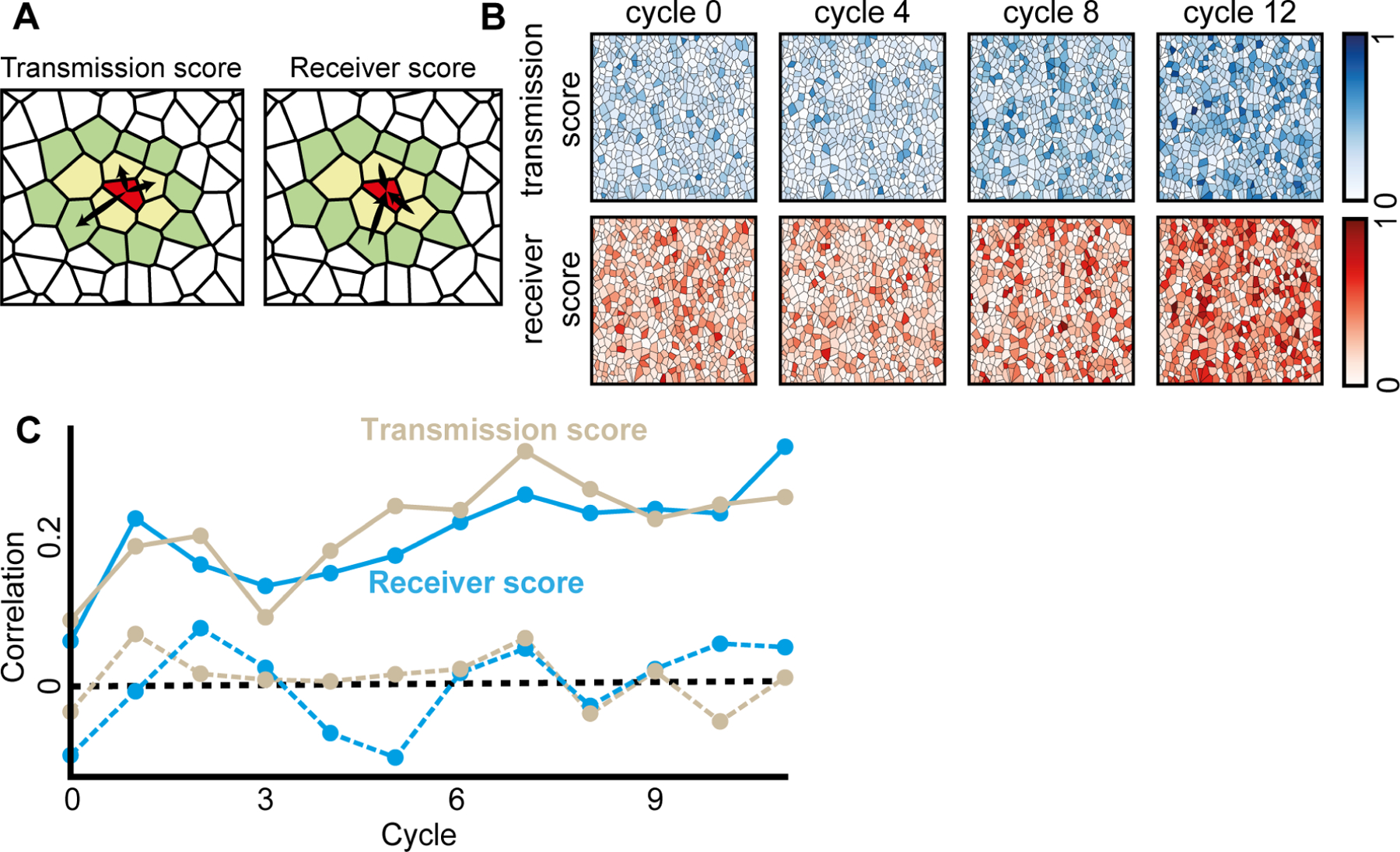
(A) The transmission and the receiver scores were calculated as the probability for a significant outgoing (respectively, ingoing) Granger Causality edge at topological distance of up to two (nearest (yellow polygons) and next-to-nearest neighbor cells (green polygons)). For example, the red cell in the center has total of 15 neighbors, 5 in topological distance 1 (yellow) and 10 in topological distance 2 (green). The transmission score of the red cell is 3(outgoing edges)/15 and receiver score is 3(ingoing edges)/15.

(B) The mean transmission and receiver scores increased over the cycles. Shown are the cells color coded according to their transmission (top, blue) and receiver (bottom, red) scores. The color scale is linear.

(C) Cells transmission and receiver scores were correlated across consecutive cycles (solid lines), reinforced over time (Pearson coefficient = 0.7512, p < 0.0001), and were a local cell property as validated with permutation analysis - shuffling the cells in the next cycle and calculating correlation (dashed line, see Methods). P-value for the significance of the memory ≤ 0.001 (except the first cycle: p-value of transmission and receiver score 0.021 and 0.15 correspondingly, and the third cycle’s transmission score p-value of 0.017, Fig. S8A).

We next asked to what extent the communication properties of cells were intrinsic cellular properties. To this end we correlated single cells’ transmission and receiver scores across the repeated mechanical stimulus cycles while testing the null hypothesis that these scores were assigned randomly between consecutive cycles. We found that single cells’ transmission and receiver scores were strongly correlated between consecutive stimulus cycles, that this correlation gradually increased as cells underwent additional stimulus cycles (Fig. 4C, Fig. S8A), and could not be explained by the autonomous cells’ response to the external mechanical stimuli (Fig. S9). Measuring single cell correlation between larger temporal gaps of 2–4 cycles did not show a dramatic diminishing pattern suggesting that the cellular memory is stable for time scales of at least 4–8 minutes, which is beyond the timescale required for the multicellular system to recover (Fig. S8B). These results suggest that cells maintain and gradually reinforce memory regarding their role in the multicellular communication network at the timescales relevant for collective synchronization.

Stability in single cell communication state and increased information flow lead to enrichment of highly communicating cells coinciding with the establishment of synchronization

We next aimed to characterize how single cell communication properties and memory contribute to multicellular synchronization. First, we normalized the transmission and receiver scores across the population and cycles by calculating the respective z-score - the number of standard deviations away from the mean (Fig. 5A, Methods). The normalized scores allowed comparison of cell communication properties across different cycles in the same experiment as well as between different experiments. Next, we partitioned the normalized transmission-receiver space into five regions and empirically assigned the cells to states according to the region they occupied. Individual cells, whose calcium dynamics were independent of cells in their local vicinity, have normalized transmission and receiver scores both below −0.5. Common cells, with average communication properties. Leader cells, with high transmission scores (transmission score > 0.5 and receiver score < 0.5), follower cells, with high receiver score (receiver score > 0.5 and transmission score < 0.5), and communication hub cells, characterized by both transmission and receiver normalized scores above 0.5 (Fig. 5A, Methods). This data-driven partitioning defined five distinct states that cells take in terms of information transfer in the multicellular communication network and enabled us to follow their evolution throughout the synchronization process (Fig. 5B–C, Video S5, Video S6). The combined effect of the increasing information flow and cell memory led to a gradual increase in the fraction of cells actively participating in communication: followers, leaders and communication hubs, along with decreased fraction of cells with reduced level of communication: common and individual (Fig. 5C).

Figure 5. Cells’ communication states, state transitions and enrichment of communication hubs.

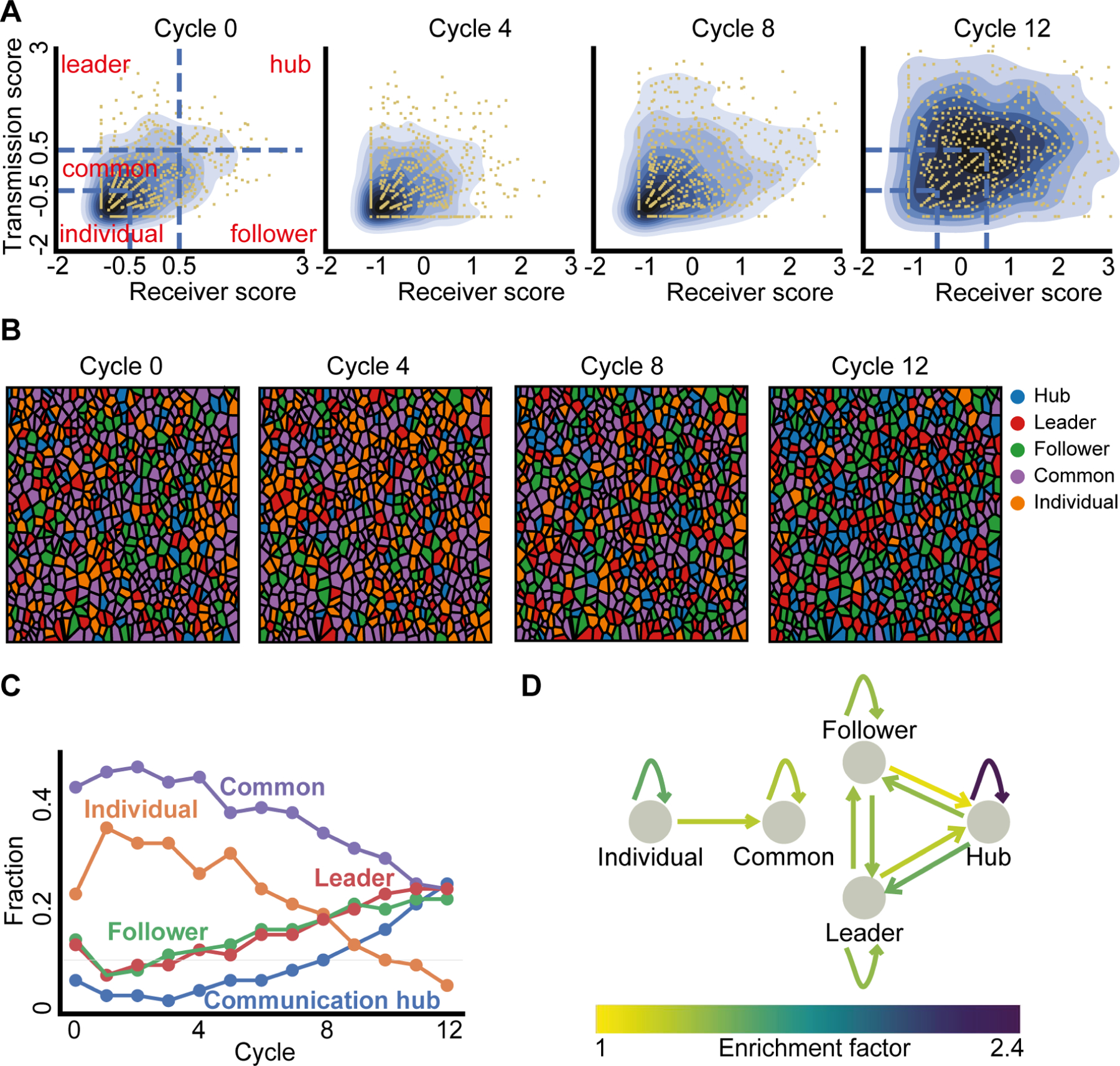
(A) Kernel density estimate plot visualization of the normalized transmission and receiver score over the cycles (blue gradient contours). Left: partitioning of the z-score normalized transmission-receiver space to five regions (blue dashed lines), each cell (yellow dot) was assigned to a group or “state” (red text) according to the region they resided at. Individual: transmission and receiver z-score < −0.5, Common: transmission z-score in the range of (−0.5, 0.5) and receiver z-score < 0.5 or receiver z-score in the range of (−0.5, −0.5) and transmission z-score < 0.5. Leader: transmission z-score > 0.5 and receiver z-score < 0.5. Follower: receiver z-score > 0.5 and transmission z-score < 0.5. Hub: transmission and receiver z-score > 0.5.

(B) Visualizing the cells’ communication states over the cycles with color code.

(C) Fraction of cells at each communication state over the cycles.

(D) Enrichment factors of cellular state transition. Depiction of the single cell transitions between states that were enriched beyond the expected values of a null model. The null model was based on the marginal distribution of the states (Fig. S10, Methods). Shown are edges with fold increase over 1 (linear color code).

To follow the dynamic trajectory of single cells between communication states we analyzed the probability of transitioning from one state to another in consecutive cycles. In particular, we computed the enrichment factor - transition probabilities between any two states and normalized the quantity by the fully random transition probabilities (Methods, Fig. S10). As expected from our earlier observation of functional memory (Fig. 4C), we found that cells tended to maintain their states or “similar” states, as reflected by self-transition enrichment factors above one (Fig. 5D, Fig. S10). Generally, single cells followed a temporal trajectory from the states characterized with less communication capacity to states with increased communication (Fig. 5D - showing edges only for enrichment factors > 1). We also found symmetric transition folds between the follower-and leader states, and the transition from communication hub to the follower/leader state was enriched compared to the opposite transition to a communication hub (Fig. 5D, Fig. S10).

We next focused our attention to the fraction of cells taking the “communication hub” role. Low fraction of communication hubs at the onset of the experiment rapidly increased to become a frequent state in later cycles (Fig. 5C) coinciding with the gradual increase in information flow (Fig. 4B). Moreover, the communication hub state was found to be much more stable than other states or transitions (2.4 fold dwell probability compared with a fully random process), underpinning their rapid spread in the population (Fig. 5C). Altogether, increased information flow along with stable functional memory led to enrichment of communication hubs that contribute to effective spread of information in the multicellular network.

Information gradually propagates from the (local) single cell to the (global) multicellular scale

Our data suggests multicellular synchronization is associated with various single cell properties such as communication state and memory. This led us to the hypothesis that the synchronization process is driven by effectively propagating information from the local scale (between single cells), to the global (collective) scale. To test this hypothesis, we measured to what extent local cell properties explained the information flow in the multicellular network. First, we computed the neighboring pair cross correlation coefficients for direct observations and spatially permuted data. We found that the spatial permutation always decreased the cross correlation, therefore cross correlation was maintained as a local cell property throughout the experiment even in the presence of common external stimuli (Fig. 6A, upper-left inset). Spatial permutation decreased the GC edge probability in early cycles but increased the edge probabilities in later cycles (Fig. 6A main panel and the lower-right inset). These results indicate that once neighboring cells reach sufficient synchronization their ability to influence each other is less effective than cell pairs far apart. We validated these observations more systematically by correlating the topological distance between pairs of cells to their GC edge probability (Methods). This analysis established that at the onset of the experiment, the information flow is dominated by local cell-cell interactions and is gradually transitioning to the global scale as the multicellular network synchronizes (Fig. 6B).

Figure 6. Gradual local to global transition in information spreading.

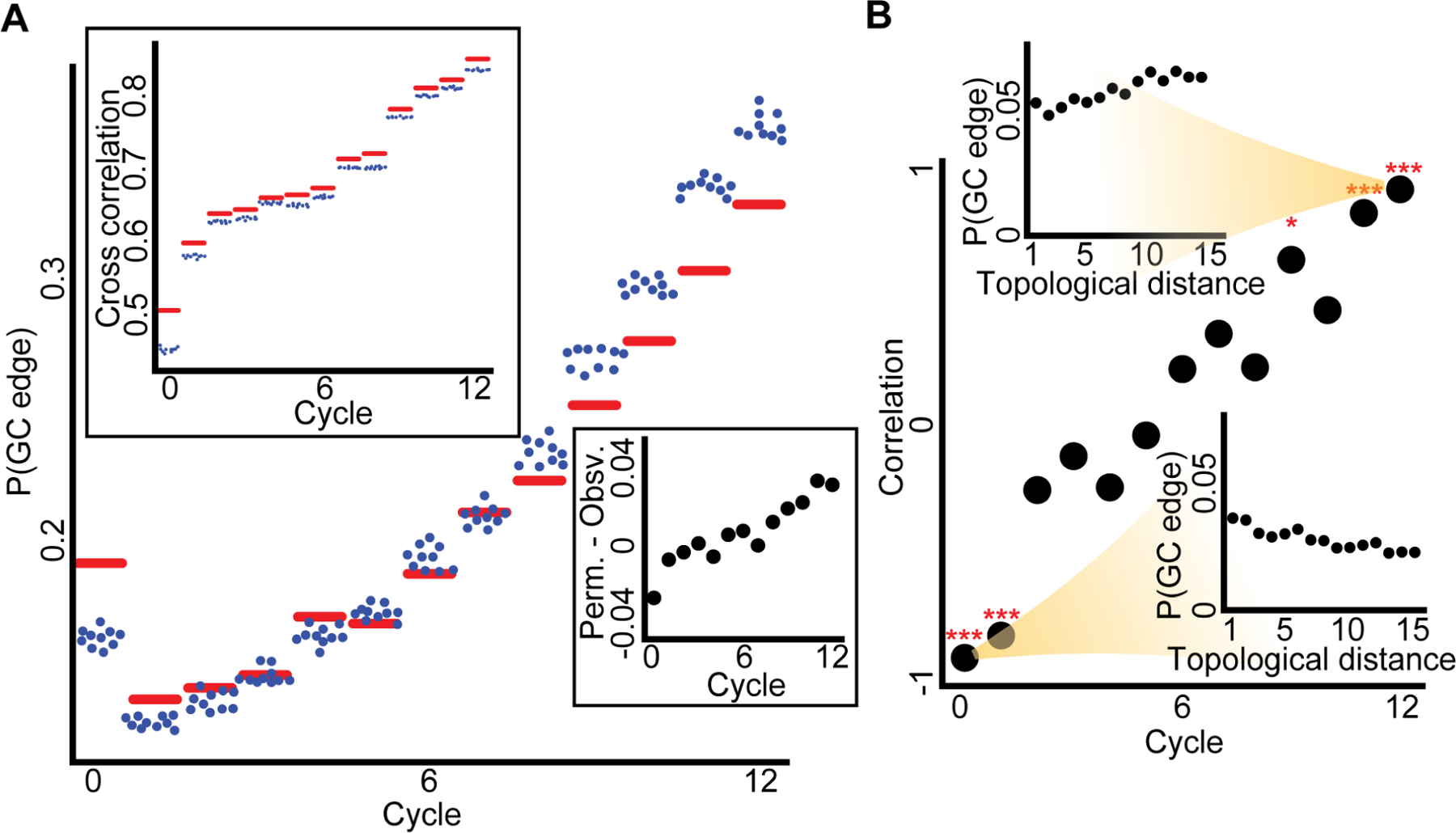
(A) Main panel: the observed versus permuted Granger causality edge probability, P(GC edge), over the cycles. Upper left panel: the mean observed versus mean permuted neighbor cross correlation over the cycles. For both panels the red horizontal line is the experimental observation, while each blue dot is the result of one of ten independent spatial cell permutations. Bottom right inset: experimental GC edge probability subtracted from the mean permuted GC edge probability using the same data as in the main panel. Through cycles 0 to 12 Pearson coefficient = 0.94, p-value < 0.0001.

(B) In the main panel each dot represents the Pearson correlation between the topological distances of pairs of cells to the corresponding GC edge probability in a given cycle. Through cycles 0 to 12 Pearson coefficient = 0.964, p-value < 0.0001. *** - p-value < 0.0001, * - p-value < 0.05, for Pearson correlation significance test. Insets show the P(GC edge) as a function of the topological distance between cell pairs for the first (bottom right) and last (top left) cycles. For this analysis, we randomly selected for each cell at each topological distance at most ten neighboring cells due to computational cost and performed FDR multiple hypotheses correction (see Methods for full details).

Discussion

The emergence of robust multicellular behaviors from heterogeneous single cell dynamics is a poorly understood, but fundamentally important phenomenon in living systems (Zinner et al., 2020). Here we provide insights in bridging the scales between local cell-cell communication and global multicellular synchronization. This was achieved by measuring asymmetric information transfer at single cell resolution in multicellular monolayers under externally applied mechanical stimuli. By employing Granger Causality to systematically quantify the communication of a cell with other cells in their local environment, we defined for each cell its capacity to transmit and to receive information in the multicellular communication network. Our method relies on local pairwise analysis of cell dynamics, and defines single cell communication properties without requiring explicit construction of the network or committing to a specific network architecture. This model-free data-driven approach can be applied to a broad set of biological systems from synchronized beating of cardiomyocytes (Nitsan et al., 2016), intercellular communication through the microenvironment (Nahum et al., 2022), brain activity (Seth et al., 2015), molecular signaling (Goglia et al., 2020) and coordinated cell migration (Malinverno et al., 2017).

We showed the cells were actively communicating with one another locally, and that physical cell-cell contacts via gap-junctions were required for multicellular synchronization. These conclusions were supported by multiple lines of evidence throughout our study. First, we reported that gap-junctions and sufficient cell confluence were required for multicellular synchronization (Fig. 3B versus Fig. 3C or Fig. S5 and Table S2). Second, we demonstrated that both local and collective heterogeneity depended on the spatial organization of cells in their vicinity (Fig. S3). Third, we found that the activation time, a cell’s autonomous response to the external stress, was not associated with the transmission or receiver score (Fig. S9A), which would also be conflicting with the gradual increase fraction of communication hubs (which are both leaders and followers). Forth, cells “remembered” and reinforced their roles in the multicellular communication network over time, as a local, spatially-dependent property (Fig. 4C, Fig. S8), but did not “remember” their activation time in previous cycles (Fig. S9B). Fifth, neighbor pair cross correlation was a local cell property throughout the experiment (Fig. 6A). Together, our data established the decoupling of the local cell-cell communication from the external stimuli, and established that the emergence of multicellular synchronization required gap-junction mediated local cell-cell communication.

Our data reveal that single cells take different roles in cell-cell communication (“division of labor”), which we defined as communication states in the context of collective mechanosensing. Cells gradually reinforce their state (“functional cell memory”), and increase the connectivity (“information flow”) in the multicellular network. These three mechanisms work in concert to facilitate the emergence of multicellular synchronization. Our results suggest that while cell heterogeneity expands the dynamic range of mechanoresponses, functional memory stabilizes the dynamics against intrinsic and extrinsic noise and that information flow sustains and reinforces the multicellular dynamics.

We found that heterogeneity in cells’ communication properties were associated with improved convergence to synchronization (Fig. 2E, Fig. 3F). We also observed that the fractions of cells at each functional state, excluding individuals, became more balanced through periodic cycles (Fig. 5C), in agreement with our conclusion that heterogeneity constructively contributes to the synchronization of a noisy multicellular system. Heterogeneity among cells could arise from stochastic gene expression levels, signaling kinetics, physiological states such as cell cycle, and/or microenvironmental cues (Cheng et al., 2015; Gut et al., 2018; Gut et al., 2015; Hasenauer et al., 2011; Muldoon et al., 2020; Paszek et al., 2010; Tay et al., 2010). Although our data does not exclude a particular source of heterogeneity, the alteration of cellular communication state at a short time scale (~10 minutes) suggests pathway kinetics, such as the cross-talk between gap junction and mechanotransduction, may be important factors to determine both local and global heterogeneities.

Previous studies have reported multiple sources of microenvironment-dependent cell memory. For instance, cells can remember past mechanical properties of their substrate, which influence their differentiation (Yang et al., 2014). Cells can also sense changes in their extracellular signal by remembering past extracellular stimulation via a receptor-mediated mechanism (Lyashenko et al., 2020), and past growth-promoting stimuli can affect cells’ future signaling responses (Spinosa et al., 2019). In the context of collective cell migration, a recent study showed that cells remembered their polarized state independently of cell–cell junctions (Jain et al., 2020), and another study revealed associative memory of electric field and chemoattractant at stimuli in a unicellular organism migration patterns (De la Fuente et al., 2019). In our study, single cell memory of communication properties contributes to the temporal evolution of the multicellular network to its synchronized state. The dissociation between a cell’s activation time and its functional role in information processing underpins the dynamic nature of memory, which is also consistent with the unidirectional evolution of the multicellular network (Figs. 5–6). While further investigations are required to reveal the molecular mechanisms of the cellular memory, we suspect slowed gap junction turnover, as well as the continuously perturbed calcium dynamics from fully relaxation, may contributed to the reinforced functional role of cells.

Our study reveals a self-organized multicellular network that supports information flow from local to global scales. Such information may be carried by two main signaling mechanisms, juxtacrine (contact-dependent) and autocrine (secreted-dependent) (Fancher and Mugler, 2017). A juxtacrine channel allows a cell to establish conversation with its (physically touching) immediate neighbors without interference from extracellular space. For HUVEC cells such communication can be realized by gap junctions (Okamoto et al., 2017). On the other hand, an autocrine channel allows a cell to broadcast its information through diffusive messengers in the extracellular space. For HUVEC cells stress-triggered ATP release and ATP-induced calcium dynamics constitute an autocrine pathway (Yamamoto et al., 2011). While both mechanisms could contribute to the information flow within the multicellular network, we suggest gap-junction and contact-dependent signaling as the dominant mechanism (Fig. 3B versus Fig. 3C or Fig. S5). While a recent study suggested that positive feedback of a diffusive signaling mechanism can drive accelerated, long-range information transmission (Dieterle et al., 2019), the external flow in our system is likely to rapidly dilute the diffusive messenger (Gregor et al., 2010). The contact-dependent information flow hypothesis is also supported by our previous studies where we demonstrated that blocking gap junctions, or inserting weakly communicating cells impaired the information flow (Potter et al., 2016; Sun et al., 2012).

Altogether, our results suggest the following phenomenological model for multicellular synchronization. Cells are gradually “learning” the local network structure around them (heterogeneity), adjusting their internal state, reinforcing it (memory), and thus stabilizing the network architecture. This stabilized network structure reduces conflicting communication interferences and thus promotes enhanced spread of information from the local to the global scale to eventually synchronize the group.

STAR★Methods

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Assaf Zaritsky (assafza@bgu.ac.il).

Materials availability

This study did not generate new materials.

Data and code availability

• Raw imaging data from a few representative experiments (step, cyclic, cyclic with gap junction inhibition), and all the processed data have been deposited at Zenodo and is publicly available. The rest of the raw imaging data will be available from the Lead Contact upon request. DOIs are listed in the key resources table.

• All original code has been deposited at GitHub and is publicly available. DOIs are listed in the key resources table.

• Scripts used to generate the figures presented in this paper are not provided in this paper but are available from the Lead Contact upon request.

• Any additional information required to reproduce this work is available from the Lead Contact upon request.

Experimental model and subject details section

Cell culture

Human Umbilical Vascular Endothelial Cells (HUVEC) were purchased from Lonza and were cultured following the vendor’s instructions. To prepare samples, cells were detached from culture dishes using TrypLE Select (Life Technologies) and suspended in growth mediums before being pipetted into the microfluidics devices at cell density of approximately 1800–2000 cells/mm² at 100% confluence (600–800 cells/mm² at 30%−50% confluence in the lower density experiments) allowing the cells to form monolayers. After overnight incubation, fluorescent calcium dye (Calbryte 520, AAT Bioquest) was loaded for 40 minutes prior to imaging. Palmitoleic acid (Sigma-Aldrich, MO) was used as gap junction inhibitor in our experiments. Palmitoleic acid was first dissolved in DMSO and then diluted to 10uM in growth medium. Before experiment, cells were treated with 10uM palmitoleic acid for 8 to 12 hours while seeding into the PDMS device. Then, 10uM palmitoleic acid was added to growth medium used for shear-stree experiments.

Methods details

Microfluidics

The organic elastomer polydimethylsiloxane (PDMS, Sylgard 184, Dow-Corning) used to create the microfluidic devices was comprised of a two part mixture - a base and curing agent - that were mixed in a 10:1 ratio, degassed, and poured over a stainless steel mold before curing at 65°C overnight. Once cured, the microfluidic devices were cut from the mold, inlet/outlet holes were punched, and the device was affixed to a No. 1.5 coverslip via corona treatment. The cross section of the flow chambers was rectangular (2 mm X 1 mm). See Fig. 1A for depiction.

Applying controlled shear stress on the cells

The microfluidics flow rate was controlled by a PID-regulated pressure pump and was monitored using an inline flow sensor (Elveflow). To verify the stability of the flow profile we mixed 1 micrometer fluorescent particles in the solution and used particle image velocimetry to quantify the flow rate (Fig. 1B). To calculate the shear stress, we approximated the flow profile in the flow chamber as low-reynolds number pipe flow. We considered the cells in the field of view to experience uniform shear stress calculated at the center of the flow chamber. This was possible because the imaging window was narrow (470 μm) compared with the chamber width (1 mm).

In the “step” experiments we exposed the cells to a “step”-like shear stress of 0.1, 0.2, 0.6, 1 or 1.6 Pa for approximately 20 minutes. In the “cycles” experiments we applied multiple rounds of 2 minute long global external periodic mechanical stimuli. We limited the number of cycles for analysis to 13 at most, because of gradual accumulation of stage drifting and photo-damaging effects. Further experiments were performed to evaluate single cell calcium signal at the stimulation onset and its relaxation time after a single pulse (Fig. S11).

Live cell imaging

We imaged the calcium dynamics of HUVEC cells using a 20X magnification oil immersion objective lens (for step-stress experiments) and a 10X dry lens (for cyclic-stress experiments, to avoid flow-induced focus drift). The fluorescent images were captured with a CMOS camera (Hamamatsu Flash 2.8) at 0.5 Hz and 1 sec exposure time. The images were stored as tif files of 960 X 720 pixels with physical pixel size of 0.65 μm X 0.65 μm (20X magnification) or 1.2 μm X 1.2 μm (10X magnification).

Measuring single cell calcium signaling

We manually annotated every cell center (Fig. 1A inset), and recorded the mean fluorescent intensity of approximately 40 μm² around the cell’s center as a proxy of the intracellular calcium signal time-series of each cell. We normalized the calcium signal according to the approach described in (Sun et al., 2013) (“response curve normalization”). The response curve of each cell was defined as $R\left(t\right)=\frac{\Delta F}{F}=\frac{\left(F\left(t\right)-F_0\right)}{F_0}$, where F(t) was calculated as the mean fluorescent intensity at time t, The baseline F₀ was calculated as the mean of the first 5 frames (10 seconds) of F(t) before the mechanical stimulation was turned on. Temporal long-pass filter smoothed the R(t) time series to reduce the effects of outliers. Temporal smoothing was performed using Python’s lowess function from statsmodels (statsmodels.nonparametric.smoothers_lowess) with the parameter frac=0.01. R(t) provides us with a dimensionless measure for the intracellular calcium magnitude relative to the cell’s basal intensity.

To evaluate the change in the calcium signal in response to external mechanical stimulus we derived the cells’ calcium signal in time: ${\widehat{R}}_l\left(t\right)=\frac{d{R}_i}{dt}\left(t\right)-〈\frac{d{R}_i}{dt}\left(t\right)〉$, where $〈\frac{d{R}_i}{dt}\left(t\right)〉$ is the mean value of $\frac{d{R}_i}{dt}\left(t\right)$, and $\frac{d{R}_i}{dt}\left(t\right)$ was calculated by Python’s numpy convolution operator over the time series with the parameter values mode=‘same’ and with a five point stencil filter [1, −8, 0, 8, −1] where the result was divided by constant of 12. A cell’s calcium signal temporal derivative ${\widehat{R}}_l\left(t\right)$ was termed calcium dynamics.

The differentiation is necessary since both the exchange of IP3 and Ca²⁺ lead to a change of calcium concentration. Hence, the derivative is quantity directly related with communication (Sun et al., 2013; Sun et al., 2012). In addition, the derivative has properties such as: independent of basal level of signal, independent of slow systematic errors such as photo bleaching, and stationarity.

Measuring adaptation rate in “step” experiments

The adaptation rate is a non-parametric measurement for the speed that the multicellular system adapts to external stress. We defined the adaptation rate as $1-\left(\frac{{\int }_{t_{max}}^{t_{max}+400}{\sigma }_{\widehat{R_l}\left(t\right)}\left(t\right)}{400\ast {\sigma }_{\widehat{R_l}\left(t\right)}\left(t_{max}\right)}\right)$, where ${\sigma }_{\widehat{R_l}\left(t\right)}\left(t\right)$ is the population-level standard deviation of single-cell calcium dynamics ${\widehat{R}}_l\left(t\right)$ at time t after applying Hampel smooth function (Hampel, 1974) to remove outliers with the parameters of window size of 10 and threshold of 3σ, and $t_{max}=\underset{t}{argmax}{\sigma }_{\widehat{R_l}\left(t\right)}\left(t\right)$ is the time of the peak variability in calcium dynamics (Methods, Fig. 1E). When a system rapidly synchronizes, the adaptation rate approaches one. Conversely, if a system maintains a large deviation between the dynamics of individual cells, the adaptation rate is close to zero. In general, a higher adaptation rate implies faster multicellular adaptation to the external stress (Fig. 1E black curve adapts faster than blue curve). which measured the ratio between the area under the curve of $\left({\sigma }_{\widehat{R_l}\left(t\right)}\left(t\right)\right)$ from the peak variability in calcium dynamics over 400 seconds (Fig. 1E, the area marked in purple area or yellow + purple area for black and purple curve accordingly) with respect to the theoretical upper bound where the relative variability is zero (Fig. 1E, the combined areas marked in yellow, orange, and purple).

We choose a temporal window size of 400 seconds (200 frames) since several experiments had late peak times defining an upper bound on the temporal window (i.e., this was the maximal time-frame without excluding experiments, Table S1).

Measuring multicellular calcium adaption using a parametric exponential model

We devised an exponential parametric model to complement the non-parametric adaption rate measurement. We fitted the exponential model A ∗ e^−Kt + C, to the standard deviation curve of the cell’s calcium dynamic using the non-linear least-squares method (Levenberg-Marquardt algorithm (Levenberg, 1944)). The initial coefficients values were set to A = 0.05, K = 0.01, C = 0. In experiments where the parameters failed to converge, we applied a linear least-squares fit to the logarithm of the signal. The coefficient K of the fitted model was used as the parametric measure for the adaptation rate.

Measuring synchronization in “cycle” experiments

We defined the asynchronization as a measure to quantify multicellular synchronization that relied on the standard deviation of single cell calcium dynamics at different time points $\left({\widehat{R}}_l\left(t\right)\right)$ in “cycle” experiments. Formally, we defined $\widehat{R}\left(t\right)={\sum }_{i=0}^n\frac{\widehat{R_l}\left(t\right)}{n}$, where n is the number of cells, as the mean calcium dynamic of all the cells at time t and ${\sigma }_{\widehat{R_l}\left(t\right)}\left(t\right)$ function as the standard deviation of the cells’ calcium dynamic. The mean of ${\sigma }_{\widehat{R_l}\left(t\right)}\left(t\right)$ was calculated over the entire cycle time. Low values implied improved synchronization across the entire group.

Granger causality

Granger causality (GC) is a statistical method to quantify the information flow among multiple variables’ time-series (Granger, 1969). Intuitively, time-series B is said to be “Granger causal” of time-series A, if the variability of A can be better explained by previous values of B and A, compared to using only previous values of A. Granger causality is an approximation to “transfer entropy” and under the assumption of Gaussian distribution it is exactly equivalent (Barrett et al., 2010).

Formally, given two-time series x_i (t) and x_j (t), where t ∈ Z. The autoregressive model of x_i is:

$$x_i\left(t\right)={\sum }_{k=1}^p{\alpha }_k{x}_i\left(t-k\right)+{\epsilon }_i\left(t\right)$$ (1)

Where, p is the lag order, the number of previous observations used for prediction, α_k is the coefficient of x_i and ε_i is the prediction error at time t. The autoregressive model of x_i based also on the previous observations of x_j is:

$$x_i\left(t\right)={\sum }_{k=1}^p{\alpha }_{ik}{x}_i\left(t-k\right)+{\sum }_{k=1}^p{\alpha }_{jk}{x}_j\left(t-k\right)+{\epsilon }_{ij}\left(t\right)$$ (2)

Where, p is the lag order, α_jk is the coefficient of x_i(t−k), α_jk is the coefficient of x_j(t−k) and ε_ij(t) is the joint error of x_i and x_j predicting x_i.

Stationarity test

To avoid spurious causality connection, x_i and x_j both must comply with a stationary process before applying the granger causality test. Intuitively, stationary means that the statistical characteristics such as average and variance of a time series are independent of time. For each cell’s ${\widehat{R}}_l\left(t\right)$ time series we applied two statistical tests for stationarity. First, Kwiatkowski– Phillips–Schmidt–Shin (KPSS) (Kwiatkowski et al., 1992) tests the null hypothesis of stationarity against the alternative of unit root. Second, Augmented Dickey–Fuller (ADF) (Cheung and Lai, 1995) was applied as a complementary test for KPSS and tests the null hypothesis for unit root against the alternative of stationary. We excluded 24 of the 47 “step” experiments where less than 85% of the cells passed both the KPSS and the ADF stationary tests with significance of below 0.05 (Fig. S2A). From the remaining experiments we considered only cells with time-series that passed both stationarity statistical tests.

Pairwise calibration of the lag order

Granger Causality is based on linear regression and thus sensitive to the lag order, i.e., the number of past time frames used to make future predictions. In the context of a time-series, the autoregressive (AR) model is the estimator of the next time point value based on its own previous values. Higher lag-order reduces the bias but increases the variance while lower lag-order reduces the variance but increases the bias (Wooldridge, 2016). We selected the lag order, for each cell pair independently, as the minimal lag derived from four methods: Akaike information criterion (Akaike, 1973), Bayesian information criterion (Schwarz, 1978), Final Prediction Error (Akaike, 1970) and Hannan–Quinn information criterion (Hannan and Quinn, 1979). The minimum lag was selected to avoid overfitting without losing information backup by using Portmanteau test which checks for whiteness (i.e, the error does not contain a pattern) (Lütkepohl, 2005).

Granger causality statistical test

We applied a statistical test to infer granger causality between two ${\widehat{R}}_l\left(t\right)$ time series x_i and x_j (denoted, GC _{xj −> xi}) (Granger, 1969). GC tests the null hypothesis that x_j is not contributing to the explained variance of x_i (Equation (2)) in relation to the model derived solely from past values of x_i (Equation (1)). This null hypothesis is rejected when at least one of the coefficients in equation (2) is different from zero. The statistic is based on the distribution:

$$F_{value}=\frac{SS{R}_{Restricted}-SS{R}_{Unrestricted}}{SS{R}_{Unrestricted}}\left(\frac{T-k}{p}\right)$$ (3)

Where, SSR_Restricted is the sum of square residuals of the model which take into account only self-previous observation of the random variable (Equation (1)), and SSR_Unrestricted is the sum of square residuals of the other model which also takes into account the previous observation of the second random variable (Equation (2)). T is the sample size (number of observations in the time series used for prediction), p is the number of variables which was removed from the unrestricted model, in our case, the lag order, and k is the number of variables, in our case, twice the lag order. The null hypothesis is rejected when the Fvalue is larger than the F statistic (i.e., F’s critical value) to conclude that $G{C}_{x_j->x_i}$. We derived the p-value from the F-statistic instead of directly using the F statistic to set up a global acceptance threshold.

Measuring collective heterogeneity

We measure the collective heterogeneity using the degree distribution of the network (Jacob et al., 2017). The measure characterizes the variability between the cell’s degrees by measuring the variation of the probability for cells with each degree k, denoted P(k). Formally, the collective heterogeneity measure is defined as $H=\frac{\sqrt{\frac{1}{N}{\sum }_{k_{min}}^{k_{max}}{\left(1-P\left(k\right)\right)}^2}}{\sqrt{1-\frac{3}{N}}}$, where N is the overall number of cells, and the numerator is considered only for all k’s such that P(k) ≠ 0. The denominator is the approximate upper bound for N cells. The collective heterogeneity measure is bounded between 0 and 1 for large networks. H= 0, when all cells have the same degree (minimal heterogeneity). H = 1, for a specific network structure when the network’s size converges to infinity, see (Jacob et al., 2017) for details. H could exceed the value of 1 for extremely small networks (see Fig. 2D). This measure is skewed for networks containing many vertices with zero degree because P(k = 0) is high and the probability for other degrees (k ≠ 0) is low, maximizing the numerator (see gap-junction inhibition experiments in Table S2).

We defined the null model for the collective heterogeneity by random shuffling the GC edges (Fig. S3A). Formally, given a graph G and binary assignment of GC edge $\alpha :\left\{\left(v_i,v_j\right)|\forall v_i\in V\left(G\right)and{v}_j\in N_{{\text{v}}_{\mathrm{i}}}\left(1\right)\cup N_{v_i}\left(2\right)\right\}\to \left\{{\alpha }_1,\dots ,{\alpha }_S\right\}$, where N_v (d) are the cells at topological distance d for cell v, α_i ∈ {0,1} is a binary edge assignment for all cell pairs at topological distance ≤ 2 from one another $\left\{\left(v_i,v_j\right)|\forall v_i\in V\left(G\right)and{v}_j\in N_{{\text{v}}_{\mathrm{j}}}\left(1\right)\cup N_{v_j}\left(2\right)\right\}$, and s is the number of such pairs. A random permutation was performed by shuffling the binary assignments. Observed collective heterogeneity was systematically higher than the null model (Fig. S3B).

Measuring local heterogeneity

We measure the local heterogeneity using the Estrada’s index measure (Estrada, 2010). The measure focuses on the more local structural aspect of the network and is based on the Randić index score that is commonly used in chemistry for describing the molecule structure (Gutman et al., 2018). In contrast to the global collective heterogeneity that measures, Estrada index is based on the degree difference between all pairs of neighboring cells, thus capturing the heterogeneity in local network structure. Formally, the Estrada index is defines as $E=\frac{{\sum }_{i,j\in E}{\left(k_i^{-\frac{1}{2}}-k_j^{-\frac{1}{2}}\right)}^2}{n-2\sqrt{n-1}}$, where n is the number of cells and k_i is the degree rank of cell i. The Estrada index is bounded between 0 and 1. E = 0, when all cells have the same degree, and E = 1, for star topological structure, where one node has a degree of n-1 and the other cells have a degree 1.

We defined the null model for the local heterogeneity by spatially shuffling the cells’ neighbors while preserving the same degree rank. We shuffle the cells’ edges by rewiring two edges while preserving their degree. Formally, given two edges e_i = (v₁,v₂) and e_j = (u₁, u₂), a single rewiring is transforming e_i, e_j edges to $e_i^{\text{'}}=\left(v_1,u_2\right)$ and $e_j^{\text{'}}=\left(u_1,v_2\right)$. The rewiring function repeated $⌈\frac{\left|E\right|}{2}\ast \log \frac{1}{\delta }⌉$ times where the repeated factor δ is 10⁻⁶ following the rule of thumb termination criteria for generating independent random graph (Ray et al., 2015).

Calculating the transmission and receiver scores

The transmission and the receiver scores were calculated as the probability for an outgoing (respectively, ingoing) edge at topological distance ≤ 2 (nearest and next-to-nearest neighbor), where the topological distance was calculated using the Delaunay triangulation.

The transmission (denoted Tr) and receiver (denoted Re) scores were calculated independently for each cell c_i using its cell neighbours at topological distance one and two $N_{c_i}\left(1\right)\cup N_{c_i}\left(2\right)$: $Tr\left(c_i\right)=\frac{{\sum }_{c_j\in N_{c_i}\left(1\right)\cup N_{c_i}\left(2\right)}{1}_{G{C}_{c_i->c_j}}}{\left|N_{c_i}\left(1\right)\cup N_{c_i}\left(2\right)\right|}$ and $Re\left(c_i\right)=\frac{{\sum }_{c_j\in N_{c_i}\left(1\right)\cup N_{c_i}\left(2\right)}{1}_{G{C}_{c_i<-c_j}}}{\left|N_{c_i}\left(1\right)\cup N_{c_i}\left(2\right)\right|}$.

We treat each cell as an independent observation thus characterizing the role of each cell in the multicellular network without specifically committing on the exact network edges. To fix spurious edges due to multiple hypothesis testing we applied the strict Bonferroni correction that defines the edge significance threshold based on the number of edges considered (Bonferroni, 1936). In our case, with a significance threshold of 0.05 and n - number of potential edges we get a new significance threshold of 0.05/n. Edges passing this strict statistical test were termed GC edges.

The reason for using topological distances of up to two in calculating the transmission and receiver score is twofold. First, for analytic reasons and second due to irregularity in cell shape. Calculating the transmission and receiver score based on a small number of neighbors will increase the uncertainty. These neighborhood sizes were determined empirically for sufficient observations for statistics, and the expected short-range communication between the cells. Topological distance of two is a sweet spot in terms of reducing the false-positive errors. Specifically, increasing the number of neighbors makes the statistical test for determining GC edges stricter (from ~0.008 for topological distance of one to 0.003 for topological distance of two) because we use Bonferroni correction to determine statistical significance (Fig. S2B). This way, the statistical test also becomes less variable between cells since the variability in the number of neighbors also decreases.

A second reason for choosing to include next-to-nearest neighbor in the analysis due to the irregular shapes of the cells (Fig. S2C). Gap junctions often connect cells that are next-to-nearest neighbors as defined by Delaunay Triangulation. Nevertheless, the main results regarding heterogeneity, memory, and local-to-global information propagation held also when considering topological distance of size one (Fig. S12).

Note that the variance in the transmission and receiver scores gradually increased over time (Fig. S13). This result is in agreement with our results associating collective heterogeneity and synchronization.

Partitioning the normalized transmission-receiver space

The transmission and receiver scores of each cell were normalized across the population to allow direct comparison of single cell heterogeneity between cycles and between experiments. We calculated the receiver and transmission z-score for each cell c_i, the variation from the mean in units of standard deviations: Tr_norm(ci) = (Tr(ci)-μ)/σ, where μ is the mean transmission score across the population over all cycles, and σ is the standard deviation. The same normalization was applied for the receiver score. Kernel Density Estimation (Scott, 2015) was used for the visualization of the 2-dimensional normalized transmission and receiver score space (Fig. 5A). We partitioned the normalized transmission-receiver space to five regions, and assigned each cell to one of these regions. Individual: transmission and receiver z-score < −0.5. Common: transmission z-score in the range of (−0.5, 0.5) and receiver z-score < 0.5 or receiver z-score in the range of (−0.5, 0.5) and transmission z-score < 0.5. Leader: transmission z-score > 0.5 and receiver z-score < 0.5. Follower: receiver z-score > 0.5 and transmission z-score < 0.5. Hub: transmission and receiver z-score > 0.5. The z-score threshold of 0.5 was selected to maintain sufficient number of cells in each role for statistical analysis.

Measuring information flow

GC edge probability was defined as the probability of a GC edge in the experiment. This was calculated as the ratio between the total number of GC edges and the total number of potential edges in the experiment (defined by topological distance ≤ 2 for each cell). Because GC edge probability is a proxy for the information flow within the multicellular network, we also used the term information flow to refer to the GC edge probability in the manuscript text.

Enrichment factor of cellular state transitions

We calculated the enrichment factor, the fold change in the observed transition probabilities of single cells from one state (functional role) to another cell state in consecutive cycles in relation to a null model derived from the expected transitions based on the marginal distribution of cells’ functional roles.

First, we constructed the single cell transition matrix $t{r}_c^{c+1}\left(i,j,k\right)$ (Equation I) where the (i, j, k) bin holds the total number of transitions of the single cell k ∈ k between state i and state j in consecutive cycles, c, c + 1 ∈ C observed throughout an experiment, and where S_c [k] indicates the state of cell k in cycle c.

$$t{r}_c^{c+1}\left(i,j,k\right)=\left\{\begin{array}{ll}1,\hfill & S_c\left[k\right]=i,S_{c+1}\left[k\right]=j\hfill \\ 0,\hfill & else\hfill \end{array}\right.$$ I.

Second, we accumulated all transitions over all cells in the accumulated transition matrix T (i, j) (Equation II).

$$T\left(i,j\right)={\sum }_{k=1}^{\left|K\right|}{\sum }_c^{\left|C\right|-1}t{r}_c^{c+1}\left(i,j,k\right)$$ II.

Third, we normalized each row of the accumulated matrix T (i, j = 1, …, |S |) to compute the Markov transition matrix $\widehat{T}\left(i,j\right)$ (Equation III), the observed probability for a cell to transition from state i to state j throughout the experiment (Fig. S10 top-left).

$$\widehat{T}\left(i,j\right)=\frac{T\left(i,j\right)}{{\sum }_{j=1}^{\left|S\right|}T\left(i,j\right)}$$ III.

Finally, we calculated the enrichment factor matrix $\ddot{T}\left(i,j\right)$, the fold change in single cell transition from state i to state j in consecutive cycles in respect to the expected probability from a null model assuming random transitions drawn from the marginal state distribution E (i, j) (Equation IV–VI, Fig. S10 bottom-left and right).

$$f\left(i\right)=\frac{{\sum }_{k=1}^{\left|K\right|}{\sum }_{c=1}^{\left|C\right|}{1}_{S_c\left[k\right]=i}}{{\sum }_{j=1}^{\left|S\right|}{\sum }_{k=1}^{\left|K\right|}{\sum }_{c=1}^{\left|C\right|}{1}_{S_c\left[k\right]=j}}$$ IV.

$$E\left(i,j\right)=\frac{u{\otimes }_{\text{outer product}}{u}^T}{u},u=\left[f\left(i=1\right),\dots ,f\left(i=\left|S\right|\right)\right]$$ V.

$$\ddot{T}\left(i,j\right)=\widehat{T}\left(i,j\right)\ast \frac{1}{E\left(i,j\right)}$$ VI.

Measuring cell memory

To measure the cell memory we calculated the Pearson correlation of the cells transmission or receiver scores between consecutive cycles with step Δt (Δt = 1 in Fig. 4C, Δt ≥ 1 in Fig. S8B). We evaluated the significance of our results using a permutation test by shuffling the cells’ spatial locations with over 1000 permutations. The permutation test was performed by concatenating the vector scores of the cycles c, c+Δt, shuffling the values, splitting back to two vectors, and calculating the absolute Pearson correlation. The p-value was set as the fraction of permutations where the shuffled correlation surpassed the observed experimental correlation. In this analysis, each stimulus cycle was considered as an independent event, although the cells’ calcium dynamics $\left({\widehat{R}}_l\left(t\right)\right)$ never reached equilibrium between cycles because the shear stress was periodic and continuous. We performed an additional experiment with rest time between the applications of shear-stress periodic cycles. Even though the system did not synchronize well (in a single replicate), positive correlations were measured between cycles, specifically before and after the idle (i.e., pause in shear stress) cycle providing further evidence that the memory is a cell property that is independent across cycles (Fig. S14).

Activation Time

The activation time of a cell in a given cycle is the time where its calcium dynamics exceeds a threshold value of γ within a cycle. The threshold is parametrized by δ in the range of 0.1, 0.2 or 0.3 from the calcium dynamics range - the initial value subtracted from the maximal value within the cycle.

$$\gamma ={\widehat{R}}_{C_i}\left(t=0\right)+\delta \ast \left(\max \left({\widehat{R}}_{C_i}\right)-{\widehat{R}}_{C_i}\left(t=0\right)\right)$$

The initial time was shifted by 60 seconds (30 frames) from the onset of the cycle to the time where the mean value of the cells’ calcium dynamics is zero to ensure that the single cell calcium signal is on the rise for the vast majority of the cells.

Correlating the topological distance between pairs of cells to their GC-edge probability

In Fig. 6B we correlated the topological distance to the corresponding GC edge probabilities. For each topological distance, for each cell, we randomly selected ten (or less in topological distances with smaller numbers) cells and calculated the GC statistical test for each cell pair in both directions. We evaluated the critical value (i.e., p-value correction) using FDR, to correct for multiple hypothesis testing. Finally, we calculated the probability for GC significant edge as the total number of significant edges divided by total GC tests performed.

Data

N = 47 biological replicates for the “step” experiments: n = 6 (0.1 Pa), n = 13 (0.2 Pa), n = 8 (0.6 Pa), n = 10 (1 Pa), n = 10 (1.6 Pa). N = 14 biological replicates for the “cycles” experiments: control n = 4 (0.1 Pa) and n = 6 (0.2 Pa), low density n = 2 (0.2 Pa), gap-junction inhibition n = 2 (0.2 Pa).

Supplementary Material

3

Video S1: A video of a representative “step” experiment with shear stress of 0.2 Pa.

4

Video S2: A video of a cyclic experiment of shear stress of 0.2 Pa.

5

Video S3: A video depicting the transmission score of a representative “cycles” experiment with shear stress of 0.2 Pa. Each region represents a single cell.

6

Video S4: A video depicting the receiver score of a representative “cycles” experiment with shear stress of 0.2 Pa. Each region represents a single cell.

7

Video S5: A video depicting the evolution of the transmission and receiver scores of a representative “cycles” experiment with shear stress of 0.2 Pa. Showing is the kernel density estimate plot visualization of the normalized transmission and receiver score over the cycles. Partitioning of the z-score normalized transmission-receiver space to five regions (blue dashed lines), each cell (yellow dot) was assigned to a state or role (red text) according to the region they resided at.

8

Video S6: A video depicting the single cell evolution in communication properties of a representative “cycles” experiment. Each region represents a single cell and the communication roles are color coded.

9

Table S1. Step experimental data table. Included are 23/47 experiments that passed the stationarity criteria (see Methods) across a shear stress range of 0.1–1.6 Pa. The following readouts were recorded for each experiment: shear stress (Pa), stationarity level (fraction of cells passing the stationarity criteria), adaptation rate (non-parametric and parametric), K (coefficient of the parametric exponential model), information flow (P(GC edge)), local heterogeneity (Estrada index), collective heterogeneity, std_length (the standard deviation in seconds), t_max_std (the peak time of standard deviation), and adaptation_rate_eow (the end of window time of the adaption rate: t_max_std + 400, see Methods).

10

Table S2. Cycle experimental data table. Included are 15 cycles experiments that include control n = 4 (1Pa), n = 6 (2Pa), gap-junction inhibition n = 2 (“palmitoleic_acid”), and low density n = 2 (“low_density”). The following readouts were recorded for each experiment: treatment, maximal shear stress (Pa), number of cycles, corr_async_vs_cycle (the Pearson correlation coefficient of the asynchronization over cycles), mean_async (the mean value of the asynchronization over cycles), mean_prob_gc_edge (the mean probability of GC edge over cycles), corr_prob_gc_edge_vs_cycle (the Pearson correlation coefficient of GC edge over cycles), corr_mem_tr/re_vs_cycle (the Pearson correlation coefficient of the transmission/receiver memory score over cycles, where the memory at cycle i is the Pearson correlation between the transmission/receiver score of i and i+1), max_mem_tr/re (the maximum value of the transmission/receiver memory score across cycles), mean_local_heterogeneity (the mean value of Esrada’s index over cycles), corr_collective_heterogeneity_vs_cycle (the Pearson correlation coefficient of the collective heterogeneity over cycles), mean_collective_heterogeneity (the mean value of the collective heterogeneity over cycles). Note that one gap-junction inhibition experiment (HUVEC_10uM_palmitolei_acid_60s_2_mbar_HUVEC_10uM_Palmitoleic_acid_60s_exp2) had high collective heterogeneity because it was dominated by cells without edges (see Methods) - 50% of the cells had a zero-degree rank.

Key resources table.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
TrypLE Select	Life Technologies	Cat#12604021
Palmitoleic acid	Sigma-Aldrich	Cat#76169
Dimethyl sulfoxide ≥99.9% USP, Multi-Compendial, J.T. Baker®	VWR	Cat#BDH1115–4LP
Krayden Dow Sylgard 184 Silicone Elastometer Kit (1.1lb)	Fisher scientific	Cat#NC9285739
EGMTM-2 Endothelial Cell Growth Medium-2 BulletKit	Lonza	Cat#CC-3162
ReagentPackTM Subculture Reagents, 100 mL	Lonza	Cat#CC-5034
Deposited data
Raw and analyzed data	This work	https://doi.org/10.5281/zenodo.6568945
Raw data of gap-junction inhibition experiments	This work	https://figshare.com/s/2e2ba004102bdd96f414
Raw data of step function	This work	https://doi.org/10.6084/m9.figshare.19807864.v1
Raw data of step function	This work	https://doi.org/10.6084/m9.figshare.19807870.v1
Raw data of cyclic pressure	This work	https://doi.org/10.6084/m9.figshare.19807873.v2
Experimental models: Cell lines
HUVEC – Human Umbilical Vein Endothelial Cells, Single Donor, in EGM™−2	Lonza	C2517A
Software and algorithms
Source code and test data	This work	https://doi.org/10.5281/zenodo.6589859
Other
Fluorescent calcium dye, Calbryte 520	AAT Bioquest	Cat#21130
CMOS camera	Hamamatsu	Flash 2.8
PID-regulated pressure pump	Elveflow	OB-1
flow sensor	Elveflow	BFS
NE-1000 One Channel Programmable Syringe Pump	New Era Pump Systems	Model#NE-1000
Corning BioCoat Collagen I-coated Flasks T-25 50/cs	VWR	Cat#12777–072
Flow switcher- 2 switch	Fluigent

Highlights.

• Endothelial monolayers synchronize calcium dynamics in response to mechanical stimuli

• Causal inference measures asymmetric information transfer at single cell resolution

• Heterogeneity, memory, and information flow enable collective information processing

• A gradual transition from local to global information spread drives synchronization