FIGURE 2.

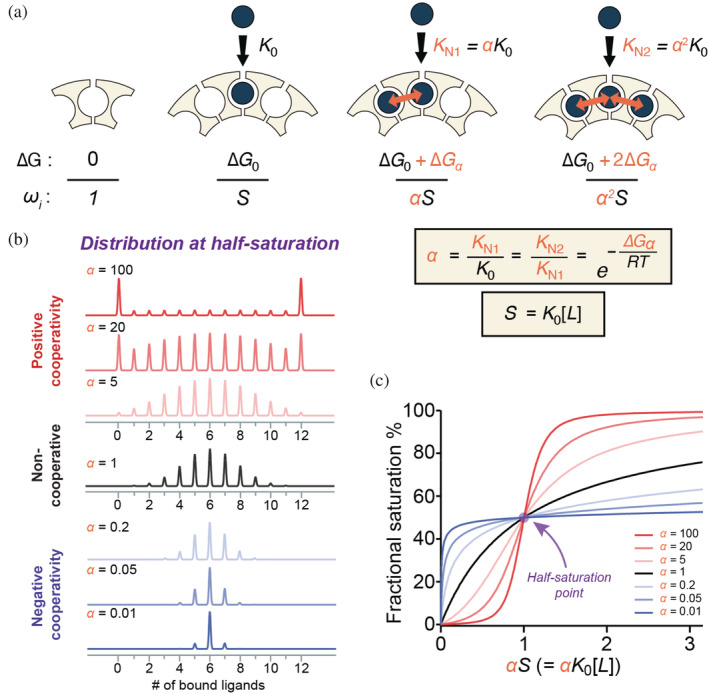
Nearest‐neighbor models can explain and predict population distributions for cooperative ligand binding to ring‐shaped oligomeric proteins. (a) In an NN model of cooperativity, four basic ligand‐binding modes can be described with two energy parameters: an intrinsic free energy change for binding to sites with no occupied neighbors (ΔG ₀), and a coupling free energy term contributed solely from each adjacent bound ligand (ΔG _α ). An empty site is defined as the reference state with ΔG ₀ = 0 and a statistical weight of 1. Binding to an isolated site is afforded a statistical weight ω = S = K ₀[L]. Cooperativity from one bound neighbor results in an association constant K _N1 = αK ₀, ω = αS, while binding to a site with two occupied neighbors is occurs with affinity K _N2 = α ² K ₀, and ω = α ² S. α values >1 indicate stronger binding to sites with occupied neighbors. The four liganded states are referred to in the text as 0, N0, N1 and N2, respectively. (b) Effect of NN cooperativity on simulated population distributions for dodecameric rings with 0–12 bound ligands at half‐saturation. Simulated populations for a non‐cooperative binding (α = 1, black), equivalent to non‐interacting sites, yield the expected binomial distribution. Population distributions arising from both positive (α > 1, red) and negative (α < 1, blue) cooperativity were simulated using a cyclic NN model. In the presence of stronger positive cooperativity the apo and holo populations dominate the distribution. In contrast, negative cooperativity favors states with half of the sites occupied. (c) Effects of NN cooperativity on fractional saturation of ligand‐binding sites. Positive cooperativity (red) generates sigmoidal binding curves, the non‐cooperative binding curve is hyperbolic (black), whereas negative cooperativity (blue) generates curves that are steeper at low concentration but shallow at high concentration. NN, nearest‐neighbor