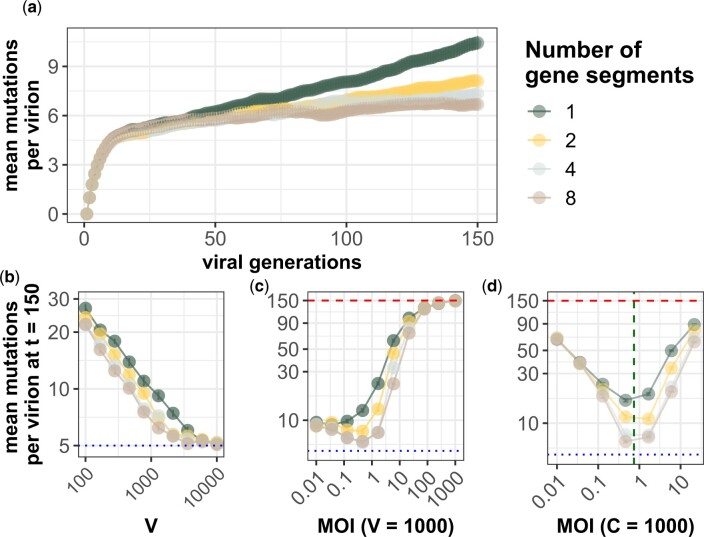
Fig. 3.
Genome segmentation slows the accumulation of deleterious mutations. In (a)–(d), the per genome mutation rate is U = 1 and the fitness cost of mutations is s = 0.2. Each data point is the average across 20 replicate simulations with error bars showing the standard error. Red dashed lines in (c) and (d) show the theoretical expectation of mutation accumulation at selective neutrality (Ut). Blue dotted lines in (b)–(d) show the expectation of mutation accumulation for an infinite viral population size at its mutation-selection balance (U/s). (a) Average number of deleterious mutations accumulated over time at a viral population size V = 1,000 and a cell population size of C = 10,000 for varying numbers of segments. b) Mean number of mutations accumulated across a range of viral population sizes with different numbers of gene segments. Reassortment slows mutation accumulation in small populations subject to Muller’s ratchet. MOI (= V/C) is kept constant at 0.1 by scaling linearly the cell population size C proportionally with the viral population size V. c) Mean number of mutations accumulated across a range of viral MOI. The virus population size is kept constant at V = 1,000 and cell population size C is modified to change MOI. Even though phenotypic hiding grows stronger as MOI increases, populations with segmented genomes experience a decrease in deleterious mutation accumulation at intermediate MOI. d) Mean number of mutations accumulated across a range of MOI. The cell population size is kept constant at C = 1,000 and the virus population size V is modified to change MOI. Segmented viral populations experience deleterious mutation accumulation when drift is strong, but benefit from reassortment as MOI increases. In both (c) and (d), mutation accumulation is slowest at intermediate MOI [dashed green vertical line (d)], balancing the effects of reassortment and phenotypic hiding. At high MOI , phenotypic hiding is nearly complete and mutations accumulate at close to the neutral rate.