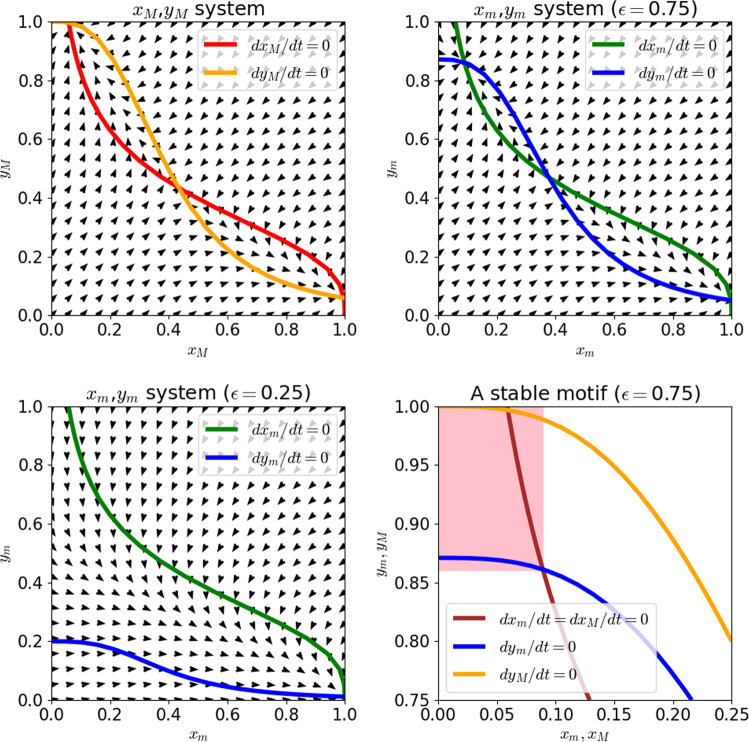
Fig. 3. Phase portraits and nullclines of the bounding systems of Eqs. 8 and 9.

The phase portrait of the bounding $x_M,y_M$ system is depicted in the top left. The trajectories of the x,y system are such that $x\left(t\right)\ge x_M\left(t\right)$ and $y\left(t\right)\le y_M\left(t\right)$. The phase portrait of the $x_m,y_m$ system is depicted in the top right and bottom left corners for two values of the parameter ϵ. For $ϵ=0.75$ (weak control strength), the system exhibits a steady state with small x and large y. Because $x_m\left(t\right)\ge x\left(t\right)\ge x_M\left(t\right)$ and $y_m\left(t\right)\le y\left(t\right)\le y_M\left(t\right)$ both hold, this steady state implies the existence of a subset of the state space that cannot be escaped by varying $u\left(t\right)$ in Eq. 6; this region is highlighted in red in the bottom right figure. Note that in the strong control case ($ϵ=0.25$), there is no such steady state in the bounding system, and thus the control is able to drive the system from a low-x, high-y state to a high-x, low-y state.