Abstract
We assessed mechanistic temperature influence on flowering by incorporating temperature-responsive flowering mechanisms across developmental age into an existing model. Temperature influences the leaf production rate as well as expression of FLOWERING LOCUS T (FT), a photoperiodic flowering regulator that is expressed in leaves. The Arabidopsis Framework Model incorporated temperature influence on leaf growth but ignored the consequences of leaf growth on and direct temperature influence of FT expression. We measured FT production in differently aged leaves and modified the model, adding mechanistic temperature influence on FT transcription, and causing whole-plant FT to accumulate with leaf growth. Our simulations suggest that in long days, the developmental stage (leaf number) at which the reproductive transition occurs is influenced by day length and temperature through FT, while temperature influences the rate of leaf production and the time (in days) the transition occurs. Further, we demonstrate that FT is mainly produced in the first 10 leaves in the Columbia (Col-0) accession, and that FT accumulation alone cannot explain flowering in conditions in which flowering is delayed. Our simulations supported our hypotheses that: (i) temperature regulation of FT, accumulated with leaf growth, is a component of thermal time, and (ii) incorporating mechanistic temperature regulation of FT can improve model predictions when temperatures change over time.
Keywords: Arabidopsis, Arabidopsis thaliana, crop simulation model, flowering time, Framework Model, FT, mathematical model, phenology, photoperiodic flowering, thermal time
Introduction
Ambient temperature during the growing season correlates with the timing of plants’ transition from vegetative to reproductive growth. Germination, organ emergence, leaf expansion, photosynthesis and respiration display similar relationships (Parent et al. 2010). These findings have led to the concept of ‘thermal time’ (Lehenbauer 1914), a metric that asserts that temperature-driven metabolic rates govern development (Zavalloni et al. 2006), and to models such as growing degree days (GDD) that use the empirical relationship between temperature and development to predict plant response (e.g. Ritchie and Otter 1985; Jamieson et al. 1998b; Chuine 2000; Jones et al. 2003; Wilczek et al. 2009; He et al. 2012; Kumudini et al. 2014).
Despite these strong correlations, our ability to predict plant responses to temperature, alone and in conjunction with other environmental factors, remains imprecise. This may be because temperatures exceed some physiologically optimal temperatures (Asseng et al. 2013; Makowski et al. 2015; Wang et al. 2015). However, plants may also respond differently to temperature fluctuations than predicted from constant temperatures falling within the same temperature range (Yin and Kropff 1996; Karsai et al. 2008), as for instance, genotype-specific increases in leaf number for rice plants exposed to 30/22 °C day/night and night/day cycles compared to constant temperature regimes ranging from 22 °C to 32 °C (Yin and Kropff 1996). These observations underscore that predictions based both on mean and constant temperatures are limited. Further, the effect of non-stressing temperatures varies among cultivars (Karsai et al. 2013), and within a single cultivar, differing day-length or climate responses may also confound model prediction. For example, the same cultivar may show different thermal-time requirements, depending on planting date, location or growth conditions across years in the same location (Piper et al. 1996; Kumudini et al. 2014; Carter et al. 2017).
Thermal time accumulation describes an aggregate of underlying plant processes, and therefore may misrepresent some responses. Thermal units accumulate more slowly during cool growing seasons than warm ones, reaching a predetermined threshold later to predict flowering. This implies that all plant physiological rates decrease in tandem with temperature decreases. However, processes do not always slow under cool temperatures. The up-regulation of cryoprotective genes (Jaglo-Ottosen et al. 1998) and the circadian clock’s buffering to temperature changes (Rensing and Ruoff 2002) are just two examples. Therefore, models using thermal time could be improved or informed by incorporating or considering the molecular and genetic underpinnings driving plant response to temperature (Montesino-San Martin et al. 2014).
More mechanistic approaches decompose environmental influences into separate model processes (Welch et al. 2003; Kim et al. 2012; Brown et al. 2013; Zheng et al. 2013; Kiss et al. 2017). One such approach, in wheat, noted that the number of leaves produced before the reproductive transition decreased as the environmental signal’s strength increased (Jamieson et al. 1998a). Prolonged cold, vernalizing temperatures followed by longer days reduced the leaf number at which the transition occurred, while ambient temperature influenced the rate the leaves were produced (Brown et al. 2013). Modelling accumulation of VRN3, a key flowering gene, in response to vernalization and day-length cues, and as a function of thermal time, accurately predicted final leaf number and timing of flowering in the constant temperatures studied (Brown et al. 2013).
Now, temperature response mechanisms in the model plant Arabidopsis thaliana are becoming understood, providing opportunities to computationally test whether they could explain the thermal time response, as well as anomalous examples. Here, we used a modelling approach, building upon the approach (Brown et al. 2013) above, to assess the mechanistic basis of plant temperature response through accumulation of the key flowering regulator FLOWERING LOCUS T (FT). Arabidopsis FT, an orthologue of VRN3 in wheat, is an integrator of environmental cues, its expression responding to photoperiod (day length), vernalization (prolonged periods of cold) and ambient temperature (Blázquez et al. 2003; Amasino 2010; Song et al. 2015). In most genotypes studied, high FT levels strongly correlate with flowering at an early developmental stage (i.e. low leaf number) (Krzymuski et al. 2015; Seaton et al. 2015; Kinmonth-Schultz et al. 2016). FT simulated as a function of day length and accumulated as a function of thermal time can accurately predict flowering in some conditions (Seaton et al. 2015). Under cool temperatures, FT is suppressed through the interaction of SHORT VEGETATIVE PHASE (SVP) and the FLOWERING LOCUS M (FLM)-β splice variant, and flowering is delayed, consistent with the concept of thermal time (Blázquez et al. 2003; Lee et al. 2013; Posé et al. 2013; Lutz et al. 2015; Kinmonth-Schultz et al. 2016; Sureshkumar et al. 2016). However, temperature fluctuations from warm to cool induce FT through induction of CONSTANS (CO), a chief transcriptional activator of FT (Schwartz et al. 2009; Kinmonth-Schultz et al. 2016). As there is no simple correlation between temperature decrease and FT level reduction, the linear accumulation of flowering gene products with thermal time may not adequately capture the influence of temperature on final leaf number, especially when temperature regimes shift over time.
In addition to direct temperature influence on FT gene expression, FT is expressed in the leaves, adding a second mechanistic layer through which temperature may impact whole-plant FT accumulation since the rate of leaf tissue production is strongly temperature-dependent (Parent et al. 2010). FT protein moves from the leaves to the shoot apex where it complexes with FD protein, a bZIP-type transcription factor, to induce the transition from leaf to floral production (Abe et al. 2005; Corbesier et al. 2007). The amount of FT protein perceived at the shoot apex likely depends on the amount of leaf tissue present. Since seasonal temperatures can be used to predict developmental rate and flowering, we aim to test the following hypotheses:
The variability in observed thermal time accumulation at flowering could be explained by the accumulation of gene product (e.g. FT protein) and the capacity for its transcript production (e.g. leaf age and area) as a plant grows.
Direct temperature influence on FT gene expression, like the direct influence of day length and vernalization, could improve model predictions in changing temperatures.
In this work, we used a mathematical modelling approach to assess the integrated influence of temperature acting at multiple scales of plant organization. To do so, we focused on FT, which correlates strongly to flowering time across a range of conditions (Corbesier et al. 2007; Salazar et al. 2009; Kinmonth-Schultz et al. 2016). We utilized earlier work in which we observed that FT could be both induced and suppressed by cool temperatures depending on whether constant or changing temperatures were applied (Kinmonth-Schultz et al. 2016). As FT is expressed in the leaves, and leaf growth is influenced by temperature, this provided us with an opportunity to determine the relative influences of FT transcriptional control versus whole-plant FT accumulation via leaf production.
We first simulated FT transcriptional control by:
Modelling FT suppression and induction by SVP, FLM and CO, based on review of previously published data, to impose dynamic control of FT over a range of temperature conditions (Fig. 1A).
Then, to simulate FT at the whole-plant level, we:
Quantified the level of FT in differently aged leaves.
Modelled the change in FT expression in leaves and plants over time.
FT transcript levels have neither been measured in leaves of different ages, nor been incorporated into flowering models, but doing so could improve our understanding of how day length and temperature impact FT to control flowering across developmental age. We incorporated these two models into the Arabidopsis Framework Model (FM-v1.0) and caused whole-plant FT to accumulate with the rate of leaf tissue production, which was modulated by temperature. Doing so required we modify FM-v1.0 to improve its capacity to simulate growth under dynamic temperature regimes (Fig. 1A).
Figure 1.
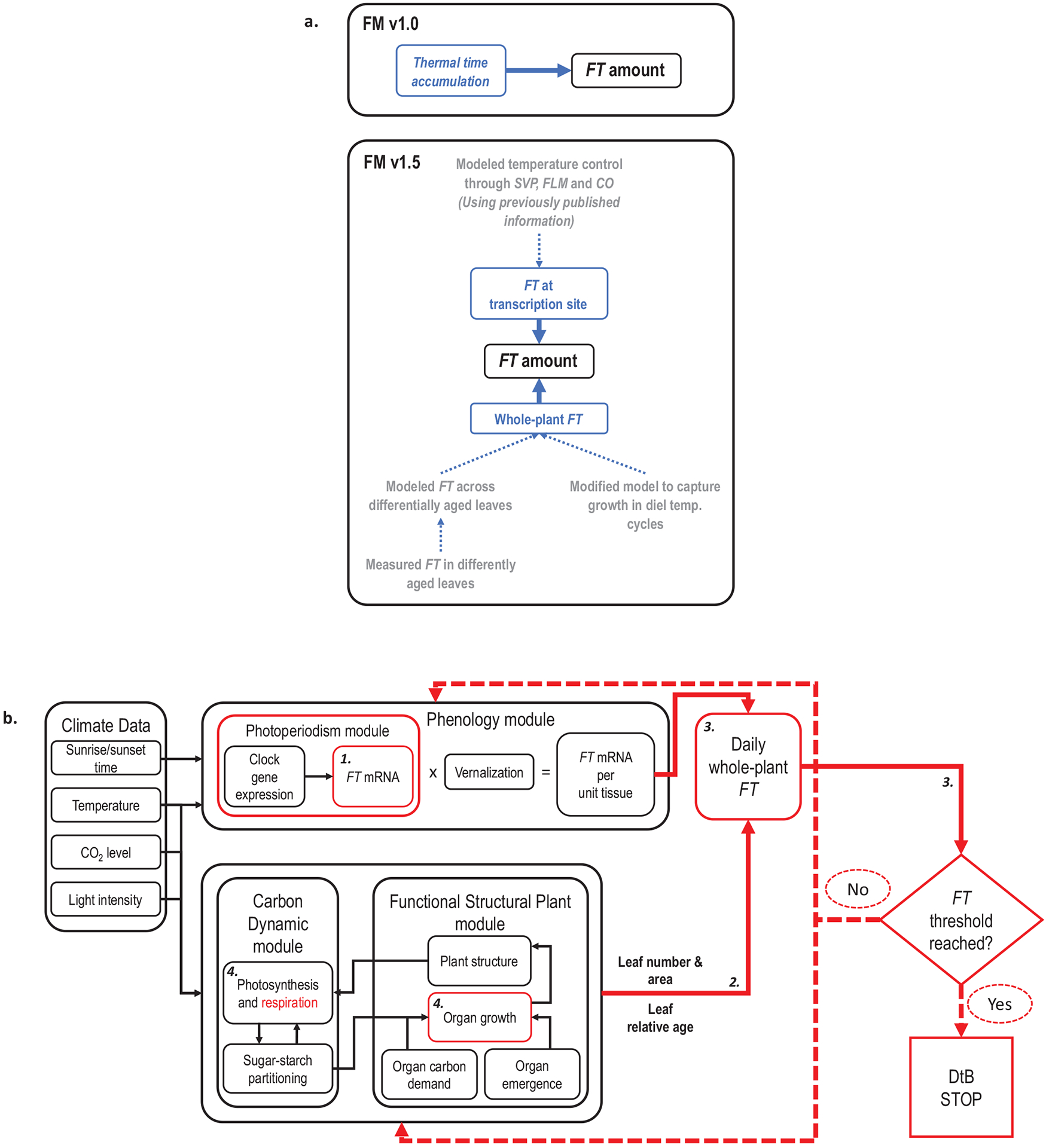
Overview of FM-v1.5. (A) Summary of how temperature influence on FT was modeled in FM-v1.0 and in FM-v1.5 (blue text) as well as the steps involved in modifying FM-v1.5 (gray text). (B) Schematic of Model FM-v1.5. Temperature (through SVP, FLM, and CO), day length, and the circadian clock regulate expression of FT in the Photoperiodism and Phenology modules per unit tissue. The leaf number and relative leaf age, outputs of the Functional Structural Plant module, are used to determine the capacity of each leaf to express FT, and leaf area is used to determine the amount of leaf tissue present. FT is summed across all leaves in a plant and added to the whole-plant FT from the previous time step. The model ceases leaf production and determines the days to bolt (DtB) when FT reaches a pre-set threshold set by using the leaf number for plants grown in long days (LD, 16-h light, 8-h dark) at 22°C, similarly to the way in which thermal units accumulate to a consistent value before a developmental transition occurs. Red illustrates where adjustments were made to the original model (FM-v1.0). The bold, italic numerals correspond to the numbers in the model description in text.
Using this altered model, referred to as FM-v1.5, we:
Explored the sensitivity of FT accumulation to both gene expression and leaf growth, as influenced by temperature.
Asked whether FT could be used to predict flowering if accumulated to a threshold like thermal time accumulates.
Explored the influence of both short- and long-term exposure to cool temperature on flowering; FT is induced and suppressed in these conditions, respectively.
Additionally, as FM-v1.0 had originally simulated FT accumulation as a function of thermal time, we compared our approach to the more traditional thermal-time approach used in FM-v1.0, which could accurately predict flowering in constant temperature conditions (Chew et al. 2014). Finally, we demonstrate situations in which our model fails to predict flowering and use those examples to discuss how our approach can serve as a framework for future work to quantitatively assess the role of FT compared with other molecular mechanisms.
Model Description
Overview
The Arabidopsis Framework Model (FM-v1.0; see Supporting Information—Fig. S1; Chew et al. 2014) combines plant growth and mechanistic flowering regulation for Arabidopsis. FM-v1.0 is run in two phases. In Phase 1, the timing of flowering is determined by thermal time accumulation (T(t) − Tbase, calculated hourly) in the Phenology module, with daytime temperature given more weight (Wilczek et al. 2009; Chew et al. 2012). Thermal time is modified by day length to produce Modified Photothermal Units (MPTUs) through mechanistic circadian- and day-length FT transcriptional regulation in the Photoperiodism module (Salazar et al. 2009). The number of days required to reach the MPTU threshold determines the stopping point of vegetative growth to mark the onset of flowering and is used as an input in Phase 2. In Phase 2, the climate parameters affect vegetative growth. Growth is determined by the rate of photosynthesis and carbon partitioning between roots and shoots (Carbon Dynamic module, Rasse and Tocquin 2006), and includes the rate of organ production as a function of thermal time, including production of individual leaves (Functional Structural Plant module, Christophe et al. 2008).
To modify FM-v1.0, we removed the thermal time accumulation used in Phase 1 of FM-v1.0 and instead incorporated mechanistic temperature influence on FT into the Photoperiodism module (Fig. 1). We maintained thermal time control over leaf tissue production in Phase 2 but modified the specific leaf area (SLA) and respiration components to improve the response of leaf growth to changing temperatures. Then, rather than running the model in two phases, we called the Phenology and Photoperiodism modules at each time step, considering their outputs FT gene expression per unit area (cm−2) of leaf tissue. We used the leaf number, age and area outputs at each time step to determine the relative FT produced by each leaf and summed the value of FT over the total leaf area of all leaves to get a whole-plant FT value. Below we detail our modifications (FM-v1.5, Fig. 1) along with a review of the data used to inform them. FM-v1.5 can be accessed at the following: https://fairdomhub.org/assays/1011.
Data review and model modifications
1. FT transcriptional regulation in changing temperatures regimes simulated through SVP, FLM and CO influence.
To impose dynamic temperature regulation on FT transcription, we incorporated previous research on the control of FT via SVP, FLM and CO. These studies compared the amounts of transcript or protein relative to an endogenous control gene, the whole-plant concentrations of which are unknown. As we are concerned currently with the relative amounts across treatments, we, therefore, expressed their values in terms of leaf area (i.e. nmol cm−2). However, when multiplied by leaf area, the units become simply nmol, and we therefore express them as such throughout. Under LD, in 22 °C day, 12 °C night temperature-cycle conditions (22/12 °C-night), FT was suppressed at dusk compared to 22 °C constant temperatures (22 °C-constant) (Fig. 2A; Kinmonth-Schultz et al. 2016) likely through the action of SVP and the FLM-β splice variant, consistent with prior observations under constant temperatures (Blázquez et al. 2003; Lee et al. 2007, 2013; Posé et al. 2013). SVP protein levels increased shortly after exposure to cool temperatures (Kinmonth-Schultz et al. 2016), as did the amount of FLM-β compared to FLM-δ splice variants (Posé et al. 2013). FLM-β facilitates SVP binding, and SVP and FLM-β protein levels increased with decreasing temperatures (Lee et al. 2013). Both SVP and FLM-β were present at 23 °C; a transfer from 23 °C to 27 °C resulted in SVP decay that occurred within 12 h (Lee et al. 2013). Based on these observations, we used a single term: SVPp to simulate the combined SVP and FLM-β behaviour representing ‘SVP/FLM activity’. Consistent with the observed behaviour of these proteins, we modelled the effect of SVP/FLM proteins (SVPp) to vary in response to temperature as shown below in equations (1.1–1.3).
| (1.1) |
| (1.2) |
SVPp-new is the rate of SVP protein (SVPp) production at time t (nmol h−1), b1 is an empirical parameter to set the SVP production rate that intercepts T = 0 °C, T is tissue temperature (°C) assumed to be equal to air temperature, b2 describes the degree SVP production decreases in response to a temperature increase and t is time of day. The influence of SVP may decline over time, as cool-temperature suppression of FT disappeared over a 2-week period [see Supporting Information—Fig. S2a]. To simulate this behaviour in FT [see Supporting Information—Fig. S2b and c], SVPceil is implemented as the ceiling of SVP production that declines relative to days post emergence of first true leaves (dFTL, equation (1.2)). SVP0 is the value of SVPceil prior to emergence of the first true leaf as determined at the time of sowing (nmol h−1). b3 determines the rate of decay over time (dFTL) and is unitless. SVPp-new is then input into a differential equation (1.3). Values and units of each coefficient are in Supporting Information—Table S1. To capture the suppression of FT at dusk, we set the SVP decay rate to be slightly lower than its production. This caused SVP to remain higher at 22 °C after a 12 °C night than in 22 °C-constant conditions, even after several hours at 22 °C [see Supporting Information—Fig. S2c]. The degradation rate is proportional to the relative amount of present SVP protein (SVPp) as represented by a rate constant (vSVP).
| (1.3) |
In LD 22/12 °C-night, FT levels were higher at dawn co-inciding with higher CO mRNA and protein in cool nights (Fig. 2A and B) (Kinmonth-Schultz et al. 2016). While SVP/FLM activity may respond to absolute changes in temperature (Lee et al. 2007, 2013; Posé et al. 2013), CO accumulation was induced by rapid changes from warm to cool (Kinmonth-Schultz et al. 2016). The degree of temperature change is likely a factor, as a drop of 10 °C (22/12 °C-night) yielded more CO transcript accumulation than did a drop of 5 °C (22/17 °C-night) relative to 22 °C constant temperatures (Kinmonth-Schultz et al. 2016). This relationship was linear across the three treatments [see Supporting Information—Fig. S3a]. Based on these observations, we correlated CO mRNA induction (KT) linearly with the difference (dT) between the maximum and current temperatures (equation (1.4)). To determine dT, the model queried the temperature at each time step, and compared the current temperature against the previous maximum temperature. If higher, the current temperature was set as the new maximum temperature. dT could have been zero if there had been no decrease in temperature, so one was added to ensure KT could not fall below one.
| (1.4) |
Coefficient c1 is an empirical parameter that scales the degree at which CO induction changes with dT. The influence of a maximal temperature change faded over several days if the temperature remained cool over that time frame [see Supporting Information—Fig. S3b]. To account for this, ddT is the time (days) since the maximal change in temperature occurred and c2 describes the decay in influence over time. KT is used to modify the CO mRNA (COm) amount to produce COm-new (equation (1.5)) to account for the temperature influence on CO through transcription (Kinmonth-Schultz et al. 2016).
Figure 2.
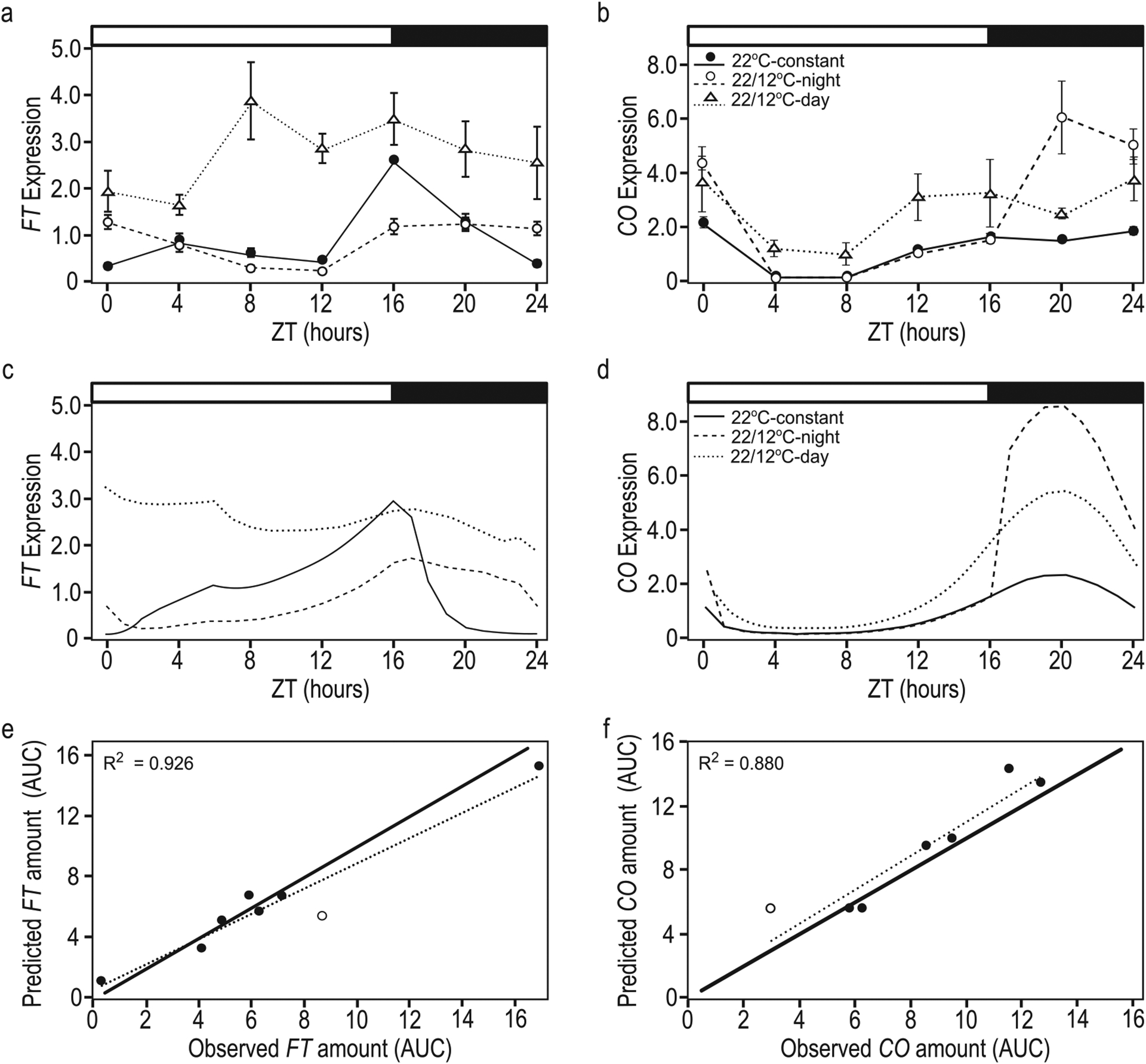
FM-v1.5 mimics general behaviours of CO and FT in response to temperature and can accommodate the overall change in amount across treatments. Observed (A, B) and predicted (C, D) diurnal patterns of FT (A, C) and CO (B, D) gene expression in warm-day, cool-night temperature-cycle (22/12 °C-night) treatments and in conditions in which the temperature dropped from 22 °C to 12 °C at dawn, then remained at the cooler temperature (22/12 °C-day) relative to the 22 °C-constant temperature control. The y-axis (A–D) is in nmol. The x-axis (A–D) is in zeitgeber time (ZT), and represents hours after dawn. The white and black bars represent light and dark periods, respectively. Error bars = 1 SE. If error bars are not visible, the SE is smaller than the height of the symbol. Correlation between predicted and observed results for FT (E) and CO (F), as calculated as the AUC 4 days after temperature treatments are imposed. Treatments include warm-day, cool-night cycles, drops to cooler temperatures at dawn, and growth from seed at constant temperatures. All treatment groups include 12, 17 and 22 °C. Dotted lines = correlation, solid lines = one-to-one line. Open circles are drop from 22 °C to 17 °C at dawn (C) growth from seed at 12 °C (F). Data from Kinmonth-Schultz et al. (2016) pooled and compiled in A and B (license to reproduce data obtained from John Wiley and Sons, #4601440806514).
With these modifications, simulated CO was induced (i.e. COm-new) in response to a change to cool temperatures both during the day and at night like that observed (Fig. 2D). There was a strong relationship between the amount of simulated and observed CO transcript across treatments, calculated as the area under the curve (AUC, Fig. 2F); although, FM-v1.5 does not incorporate the CO suppression observed when plants are grown at constant 12 °C from seed (12 °C-constant) (Kinmonth-Schultz et al. 2016).
COm-new was used as an input to determine CO protein (COp) as in Chew et al. (2014), as shown below (equation (1.6)). CO protein degradation occurred only in the dark period (L1 = Light period).
| (1.5) |
| (1.6) |
As several factors converge to regulate FT at its promoter (Bratzel and Turck 2015), we hypothesized that the SVP/FLM complex and CO acts competitively at the FT promoter, with CO overcoming suppression by SVP/FLM at night when its levels are high. The Photoperiod module in FM-v1.0 (Chew et al. 2014) describes the direct relationship between transcription of FT mRNA (FT m) and CO protein (equation (S1.1)). We modified this equation to incorporate the interaction between CO and SVP/FLM using a modified Michaelis–Menten function for competitive inhibition (Segal 1976), such that the K of FT induction by CO was influenced competitively by SVP/FLM activity as below.
| (1.7) |
The uppercase V and K, and lowercase v and k are Michaelis–Menten constants either describing the FT synthesis rate as influenced by CO protein (COp), SVP/FLM activity (SVPp) or FT degradation. We observed CO and FT induction when the temperature dropped both at dawn and dusk (Kinmonth-Schultz et al. 2016), like previous observations (Thines et al. 2014). However, observed daytime CO induction was lower than nighttime induction while daytime FT induction was higher (Fig. 2A and B). The daytime CO protein production captured in equation (1.6) was not enough to capture the daytime behaviour of FT in FM-v1.5 in response to daytime drops in temperature. While dusk regulation of FT is well understood (Song et al. 2015), the factors influencing morning FT induction are only beginning to be elucidated (Song et al. 2018). To capture the observed behaviour, we increased FT transcriptional sensitivity in the morning (L2) using a switch function that relied on a model component that peaks around dawn, specifically the circadian clock component, LHY, from the Photoperiodism module [see Supporting Information—Fig. S4].
With these modifications incorporated into the model, CO induced higher FT at dawn when temperatures dropped at night (22/12 °C-night), and higher FT throughout the day when temperatures dropped just after dawn (22/12 °C-day) as previously observed (Fig. 2C). Our simulation in which SVP/FLM activity decay was slower than production caused residual SVP/FLM activity at dusk [see Supporting Information—Fig. S2c], suppressing FT at dusk as observed (Fig. 2C, 22/12 °C-night). When we removed SVP influence to mimic a svp mutant, dusk FT suppression disappeared as observed [see Supporting Information—Fig. S5]. However, morning levels of FT in a simulated svp mutant were higher than observed, perhaps because we increased morning FT transcriptional sensitivity to CO. This high induction was necessary to approximate the observed behaviour of FT in wild-type, especially the very high daytime induction observed when the temperature drop occurred at dawn (22/12 °C-day). Therefore, while SVP, FLM and CO may act competitively to regulate FT, additional mechanisms likely increase FT transcription, perhaps in a time-dependent manner, despite the presence of SVP and FLM repression in cool temperatures.
For flowering to occur, favourable conditions must occur over several days (Corbesier et al. 2007; Krzymuski et al. 2015; Kinmonth-Schultz et al. 2016). Our aim was to approximate FT behaviour within a day and through time. Observed FT suppression at dusk in 22/12 °C-night conditions occurs by Day 2 of the temperature-cycle treatment relative to the 22 °C-constant control [see Supporting Information—Fig. S2a]. This was true with FM-v1.5 as well, although FT levels continue to decline until Day 4 [see Supporting Information—Fig. S2b]. Over 2 weeks, the increase in dusk FT levels in 22/12 °C-night conditions relative to the 22 °C-constant control was similar between observed and simulated data [see Supporting Information—Fig. S2b]. In sum, FM-v1.5 can accommodate the wide range in FT transcribed across temperature treatments (Fig. 2E), and FT behaves similarly over time to that observed, allowing us to explore the temperature influence on FT expression and flowering in LDs.
2. Incorporating FT as a function of leaf and plant age.
As our aim was to simulate whole-plant FT accumulation with leaf growth, we needed to ascertain whether FT expression was consistent across all leaves produced and across all ages. SD-grown (8 h light, 16 h dark) plants aged 2, 3, 4 and 6 weeks exposed to LDs for 3 days to temporarily induce FT as in Corbesier et al. (2007) showed differing capacities to express FT. (SDs cause a delay in the transition to reproduction in Arabidopsis, and the lines used do not transition to reproduction in these time frames, as in 8-week-old plants in Corbesier et al. (1998)). In young plants, even very young leaves expressed FT. This capacity changed as plants age (Fig. 3; see Supporting Information—Fig. S6). Newer leaves in older plants seemed to lose capacity to express FT (Fig. 3; see Supporting Information—Fig. S6), even those that had expanded. Considering FT copy number per unit leaf tissue, the amount of FT increased from the cotyledons to the older true leaves in plants aged 2, 4 or 6 weeks in LD, declining again in more newly produced leaves (Fig. 3A–D; see Supporting Information—Fig. S6). In 6-week-old plants, several of the newest leaves showed FT expression levels comparable to those in SD conditions (Fig. 3C and D), even in leaves that had expanded to sizes that were comparable or larger than leaves of plants expressing FT at a younger age. Using pFT:GUS (Takada and Goto 2003) plants to assess the location of FT on a per area basis, FT increased from cotyledons to the true leaves (number 2, Fig. 3E) then declined again in more newly produced leaves. For several of the true leaves on the younger plants, pFT:GUS staining spanned the tip to the base of the leaves [see Supporting Information—Fig. S6a and b]. In 6-week-old plants most leaves sampled showed staining only at their edges regardless of leaf size [see Supporting Information—Fig. S6d]; remnant staining appeared to occur throughout the blade of older leaves. Both analyses suggest that in addition to leaves losing the capacity to express FT as they age, newer leaves in older plants also lose the capacity to express FT. We incorporated the relationship describing FT expressed per unit leaf tissue into FM-v1.5. Future work to address the mechanisms for this change with developmental age is needed.
Figure 3.
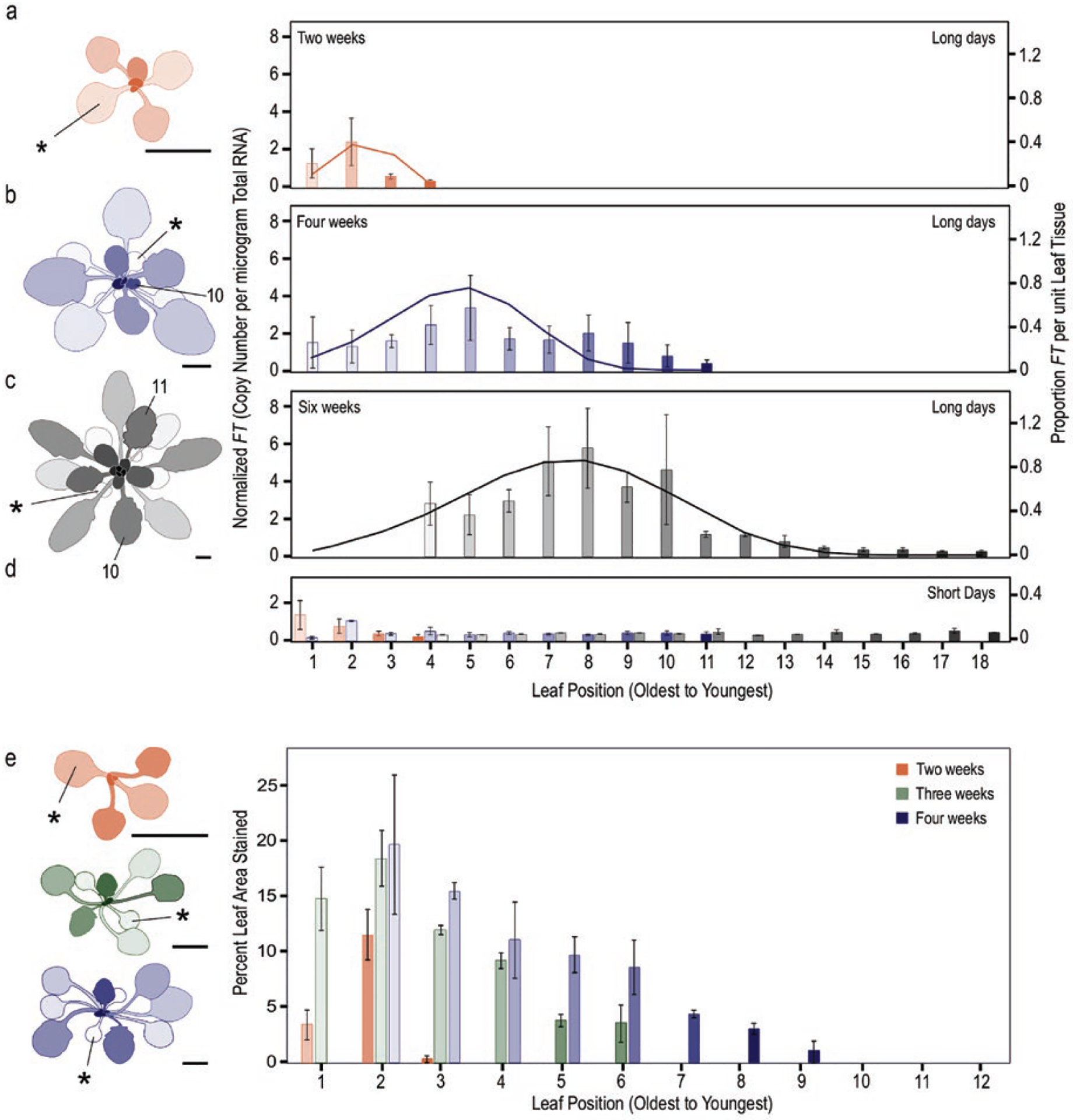
FT expression declines in later produced leaves. Leaves of short-day-grown plants, that had not yet transitioned to flowering, aged 2 (A), 4 (B) and 6 (C) weeks old were exposed to long days or short days (D) for 3 days, then harvested at 16 h after dawn on the third day to determine FT amount per leaf. The colours in (D) correspond to the colours and ages in panels (A–C). FT levels were determined by absolute copy number and normalized within a replicate. The simulated proportion of FT per unit leaf tissue (cm−2, solid lines) for each plant age is shown. This value was used in FM-v1.5 as a modifier to adjust the amount of FT produced by each leaf. Percent of the leaf area showing staining in pFT:GUS plants (E). For all, the two cotyledons and first two true leaves were pooled for each sample as they emerge in pairs. The youngest leaves, just emerging at the apex (1–2 mm in length) were also pooled. Older leaves in the 6-week-old plants failed to yield 2 μg total RNA and were excluded. For each plant inset, asterisk indicates one of each cotyledon pair (*). The 10th and 11th leaves to emerge are labelled. The shading of the bar graphs (light to dark) indicates leaf age (oldest, first to emerge, to youngest) and corresponds to the shading in the plant insets. Scale bars = 0.5 cm.
To simulate the proportion of FT per unit tissue (FT, nmol cm−2) of each leaf, we used a beta function (Yin et al. 1995) based on relative leaf age (r), beginning with the youngest emerged leaf as leaf one.
| (2.1) |
βFT yields a value between zero and no more than one but can be lower depending on plant age as measured by leaf number. βFTmx scales, based on total leaf number, the maximum value that can be attained by a leaf of a single plant, Ropt is the relative age at which that maximum value is attained, Rcrit is the oldest leaf that can express FT and e described the steepness of the curvature. This function caused the dependent variable to oscillate if the independent variable spans a broad range. To avoid this behaviour, we set βFT to be zero below and above the relative ages where βFT first attains a minimum. βFTmx and Ropt are dependent on the total number of leaves on a plant (l), as described below, avoiding the need to reparameterize for plants of different ages. g1 and g2 are empirical coefficients.
| (2.2) |
| (2.3) |
3. Determining whole-plant FT levels and accumulating FT to a threshold.
To link FT transcript accumulation to leaf tissue production, the Phenology module was called at each time step. We considered the output of the Phenology module to be the amount of FT produced per unit leaf area (FTleaf, nmol cm−2) in order to scale for total FT at the whole-plant level. The whole-plant FT level (FTplant) was determined by a summation of all FTleaf adjusted by individual leaf area (LA, cm2) and the capacity of each leaf to express FT (βFT, unitless modifier) as FT induction is dependent on light intercepted by the leaf.
| (3.1) |
At each time step, FTleaf (nmol cm−2) was determined for each leaf, summed across all leaves and added to the value from the previous time step to determine whole-plant FT levels on a per area basis, which can be converted to FT per unit mass using the leaf mass ratio as needed. Such FT accumulation was consistent with the observation that several days of FT induction are needed to induce flowering (Corbesier et al. 2007; Krzymuski et al. 2015; Kinmonth-Schultz et al. 2016). To predict flowering, the model ran until a threshold level of FT was reached at the whole-plant level (FTthrsh). We set the threshold as the value of FT accumulated when plants reached 15 and 8 leaves [see Supporting Information—Table S1], which was the nearest whole number to the average leaf number at bolt for Columbia-0 (Col-0) and Landsburg erecta (Ler), respectively, grown in LD 22 °C-constant conditions (Kinmonth-Schultz et al. 2016). We maintained the strain-specific parameters for rate of emergence and leaf initiation from FM-v1.0, as they were comparable to our results (Fig. 5A), but added a 7-day delay after initiation of the final leaf to improve the fit across strains at 22 °C. This was to account for the time between initiation of the leaf primordia as modelled (Christophe et al. 2008) and growth of a visible bolt, counted when the stem below the bolt head was 2 mm in length (Kinmonth-Schultz et al. 2016).
Figure 5.
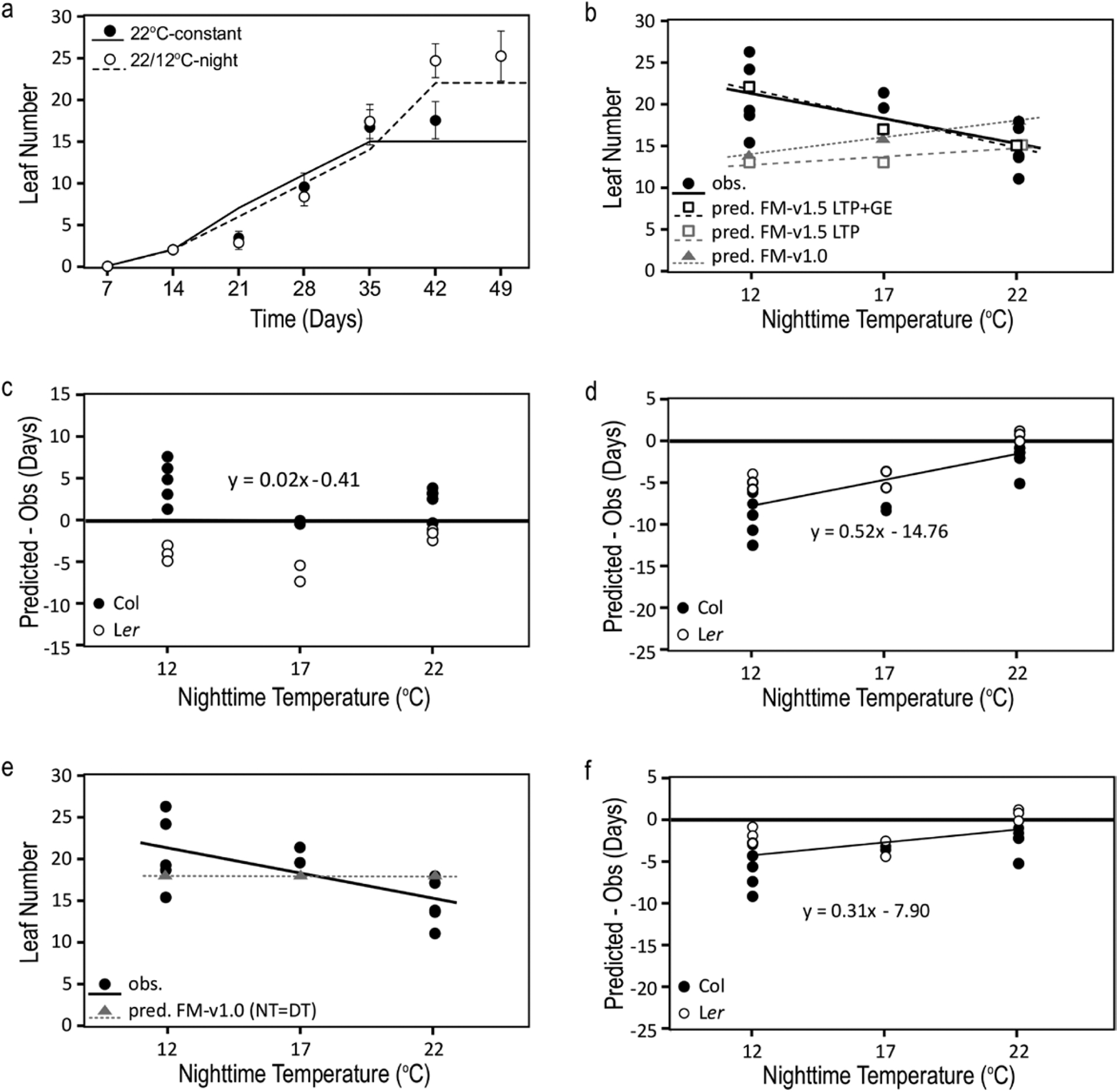
FT accumulation as influenced through CO and SVP/FLM and leaf tissue production can improve model predictions in changing temperature conditions compared to MPTUs. (A) Comparison of simulated (lines, FM-v1.5 LTP+GE) and observed (symbols) leaf number by week in Col-0 in constant 22 °C conditions (22 °C-constant) and in 22 °C-day, 12 °C-night temperature cycles (22/12 °C-night). (B) Final leaf number of Col-0 at bolt as observed (obs.) and predicted (pred.) by incorporating temperature influence on FT though leaf tissue production (LTP) and FT gene expression (GE) (FM-v1.5 LTP+GE), leaf tissue production only (FM-v1.5 LTP), and through traditional MPTUs (FM-v1.0). (C, D) The difference between predicted and observed days to bolt in Col-0 and Landsberg erecta (Ler) using FM-v1.5 LTP+GE (C) and MPTUs in FM-v1.0 (D). (E) Observed and predicted final leaf number and (F) the difference between predicted and observed results using MPTUs in FM-v1.0, adjusted so that daytime and nighttime temperatures are given equal weight. (B–F) Plotted over three nighttime temperatures. Daytime temperature was 22 °C. (C, D, F) Horizontal line at zero is the position in which there is no difference between predicted and observed results. Error bars = 1 SD. If error bars are not visible, the SD is smaller than the height of the symbol. Observed leaf number and days to bolt pooled and compiled from Kinmonth-Schultz et al. (2016) (license to reproduce data obtained from John Wiley and Sons, #4601440806514).
Here, we considered whole-plant levels of FT, rather than the amount reaching the shoot apex, consistent with typical molecular studies that consider gene expression at the level of the whole plant (Imaizumi et al. 2003; Valverde et al. 2004). Through this approach, we inherently assumed that the rates of translocation of FT to the shoot apical meristem and the proportion of whole-plant FT perceived at the shoot apex are similar across treatments. All other treatments were run to this threshold under the assumption that it remains conserved under different growing temperatures.
In FM-v1.0, the development rate towards flowering, as influenced by FT amount and photoperiod, was limited below and above two critical day lengths (10 and 14 h) using a different parameter set for each photoperiod (Chew et al. 2014).
| (3.2) |
We removed this function and considered direct FT accumulation. Determining the absolute amount of FT required to induce flowering and whether there are threshold levels of transcription, below and above which flowering time is unaffected, will be a useful future study. We maintained the vernalization component from FM-v1.0 to maintain model flexibility, as vernalization should modify overall levels of FT (Helliwell et al. 2006; Searle et al. 2006). This value fell between zero and one and now modified the levels of FT produced within the Phenology model rather than modifying the thermal unit accumulation rate.
4. Adjusting FM-v1.0 leaf area response to changing temperature regimes.
FM-v1.0 was parameterized for constant temperatures. It captured the leaf areas of plants exposed to different constant temperatures but simulated larger areas for plants grown in temperature regimes that change over time than the constant-temperature control [see Supporting Information—Fig. S7a]. Conversely, observed plants accumulated similar biomass, but a lower SLA (m2 g−1) under changing temperatures relative to a constant-temperature control (Pyl et al. 2012). Therefore, in FM-v1.5, we adjusted the SLA and respiration components to improve the relationship among leaf areas across changing temperature conditions (described below).
The larger leaf area in FM-v1.0 under a temporal shift in temperature regime, specifically a drop in temperature, occurred for two reasons. First, SLA was observed to decrease with increasing thermal time (i.e. developmental time, Christophe et al. 2008). When incorporated into FM-v1.0, this relationship caused simulated SLA to be lower in warmer conditions because development was faster [see Supporting Information—Fig. S7b and c] although all treatments began at a similar biomass. Second, FM-v1.0 related maintenance respiration to temperature using the Arrhenius function, causing respiration to be lower under cooler temperatures. Under warm daytime temperatures, plants simulated in changing temperatures accumulated the same amount of stored carbon as the control [see Supporting Information—Fig. S7d]. However, once shifted to cooler temperatures, the lower simulated maintenance respiration rate [see Supporting Information—Fig. S7e] left a larger stored carbon pool that could be used for growth, causing larger leaves in FM-v1.0.
Respiration, carbon storage or growth may be altered by temperature in ways not captured in the model. In cold-tolerant woody species, respiration of stem cuttings increased near freezing, rather than following the trend predicted by the Arrhenius function, as did the pool of non-structural carbohydrates (NSCs) (Sperling et al. 2015). Respiration may also increase at more moderate temperatures in cases where freezing tolerance is induced, as in Arabidopsis at 16 °C in light with a low red/far-red ratio (Franklin and Whitelam 2007). In chrysanthemum, cool nighttime temperatures decreased leaf area while increasing dry weight, by increasing stored starch (Heinsvig Kjær et al. 2007). FM-v1.0 did not incorporate these complexities nor consider sinks for carbon other than growth, such as NSCs. Therefore, to simulate the relative relationships in leaf area across the temperature conditions needed for our study, we removed the temperature sensitivity of maintenance respiration and adjusted the SLA (m2 g−1) to decline with decreasing temperature using observations from Pyl et al. (2012) [see Supporting Information—Fig. S8]. This resulted in lower SLA across treatments than the control when there was a temporal shift to cooler temperatures [see Supporting Information—Fig. S7f]. A more accurate representation of respiration and carbon pools should be incorporated into future models to improve plant growth predictions in a range of temperature conditions.
Model parameterization
To entrain the diurnal FT and CO patterns, we incorporated previously published data from three different treatment types all in 16-h photoperiods grown at ~60 μmol m2 s−1 photon flux density: warm-day (22 °C), cool-night (12 or 17 °C) temperature cycles, in which the temperature change occurred at dusk (24 wild-type replicates, six including 17 °C, and five including the svp mutant line); constant warm (22 °C) temperatures shifting to constant cool (12 or 17 °C) temperatures at dawn (eight and three replicates, respectively); and growth at 12 and 17 °C from seed (three replicates each) (Kinmonth-Schultz et al. 2016) (pooled data shown in Fig. 2A and B, see Supporting Information—Figs S3a and S9a). Except for where ‘growth from seed’ is specified, plants were moved to temperature treatments after 1 week in 22 °C-constant temperature conditions. In all instances, growth from seed at 22 °C was used as the control. The temperature-cycle harvests including 17 °C spanned 2 days. An ANOVA comparison of models including and excluding day as a factor, showed no difference. The days were counted as separate replicates for model training. FT and CO gene expression were pooled across all replicates within a treatment and normalized across treatments to the mean peak FT expression (ZT 16) and mean peak CO expression (ZT 16 and 20 mean) in the 22 °C control. Parameter values for change in CO induction and SVP/FLM activity over a period of days were determined using experiments with four replicates each (Kinmonth-Schultz et al. 2016) (data shown in Supporting Information—Figs S2a and S3b). As we were interested in the cumulative influence of FT, we assessed model fit and performance in three ways: (i) minimizing RMSE between observed and predicted gene expression profiles over the 24-h harvest period (14 days after sowing), (ii) comparing observed and predicted amounts of CO and FT as calculated as the AUC 14 days after sowing and (iii) maintenance of gene expression patterns through time.
Experimental Methods
Plant growth conditions
For all previously published and new plant growth experiments used in this work, seeds were sewn onto soil (Sunshine #3 Mix; Sun Gro Horticulture) containing Osmocote Classic time-release fertilizer (Scotts) and Systemic Granules: Insect Control (Bionide), cold and dark stratified at 4 °C for 4 days, then moved to temperature treatments in either long-day (LD, 16-h light, 8-h dark; light intensity = ~60 μmol m2 s−1) or short-day (SD, 8-h light, 16-h dark; light intensity = ~140 μmol m2 s−1) conditions as previously described (Kinmonth-Schultz et al. 2016).
To explore the effect of conditions in which FT is suppressed (Fig. 6), we grew Col-0 at 12 °C from seed (12 °C-constant) or in 22 °C for 1 week then moved plants to 12 °C within 2 hours after dawn (22/12 °C-day). To explore the influence of short-term temperature fluctuations (Fig. 7), we grew Col-0 plants in SDs for 2 weeks, opposed to the 1 week in experiments used to parameterize mechanistic temperature control of FT, to ensure they had two to three true leaves and were competent to flower. We then exposed them to 12 °C in LDs for 2, 4 or 6 days (12 °C-2d, -4d or -6d). After treatment, plants were moved to warm, LD conditions. Control plants were moved directly to warm, LD conditions at 2 weeks. The chambers used for the warm conditions averaged 24 °C. This was incorporated into simulations.
Figure 6.
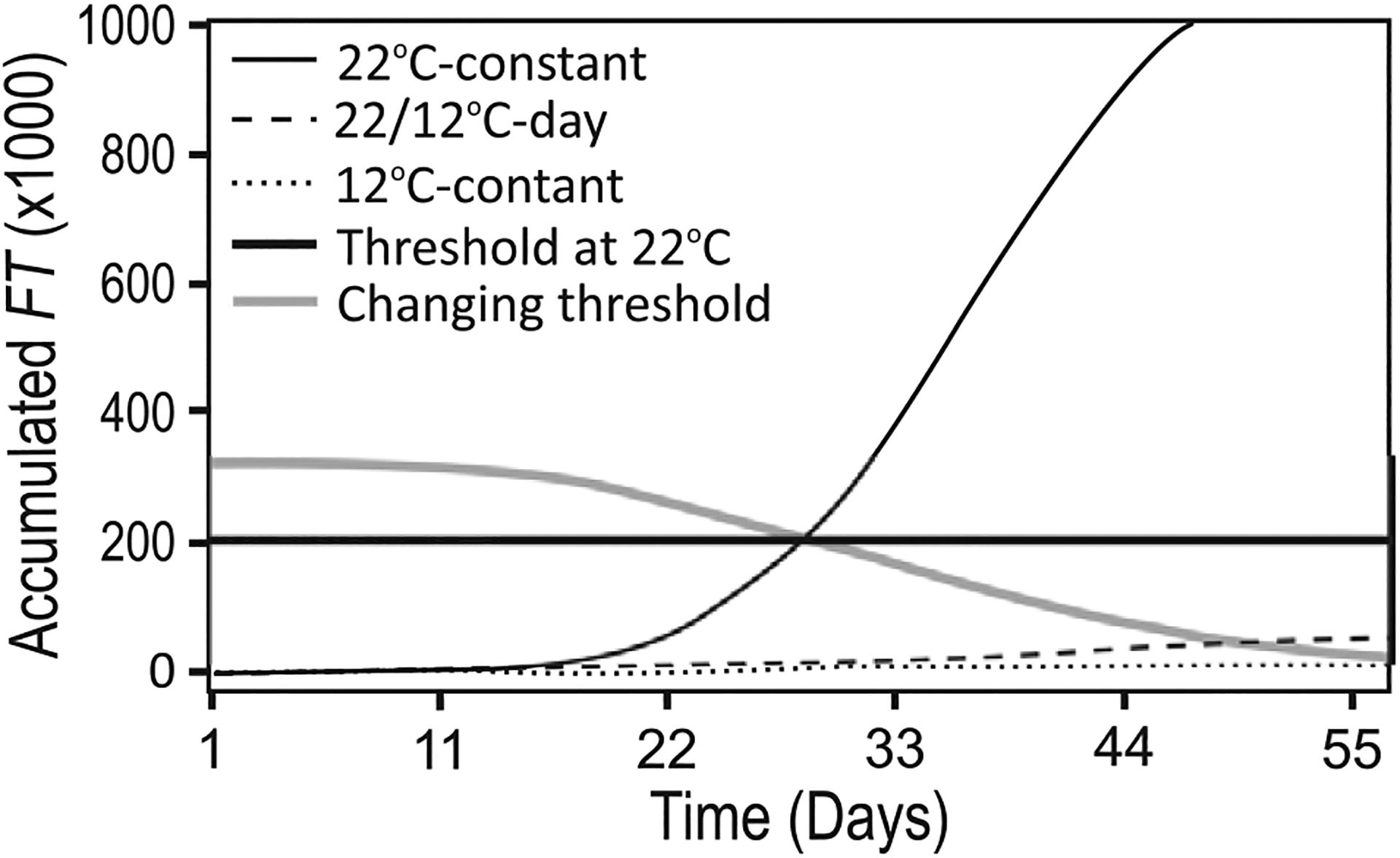
FT fails to accumulate to a threshold in some cool-temperature conditions. Plants grown at constant cool (12 °C) temperatures from seed (constant) or after 1 week at 22 °C (22/12 °C-day) do not accumulate FT to a threshold set using 22 °C constant temperatures in long days (thick black line). Altering the threshold to decline with developmental time (thick grey line) improves the predictive capacity of FM-v1.5, as we propose in the discussion.
Figure 7.
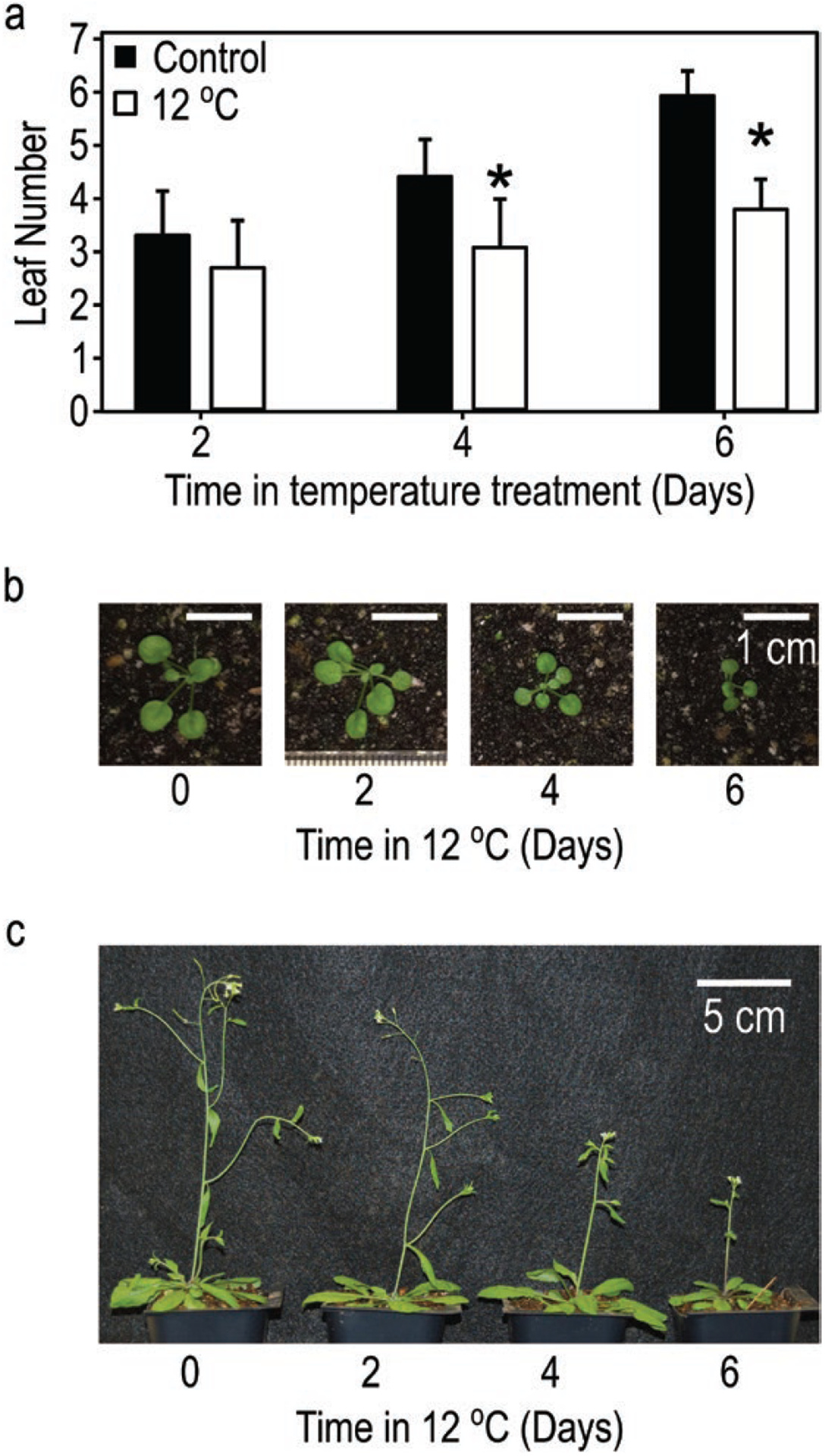
Growth is slowed and flowering is delayed in plants exposed to 12 °C for 2, 4 or 6 days, then returned to warm temperatures (24 °C), relative to control plants grown continuously in warm temperatures. (A) Average leaf number of plants recorded at dawn after 2, 4 or 6 days in 24 °C (control) or 12 °C temperature conditions. (B) Relative seedling sizes on dawn of Day 7, after completion of all cool-temperature treatments (scale bars = 1 cm, 0 = control). Individual images cropped from the same photograph and scaled together (see original image, Supporting Information—Fig. S11). (C) Relative flowering progression 3 days after appearance of last floral stem (bolt) in plants exposed to 12 °C for 2, 4 or 6 days relative to 24 °C control (0, scale bar = 5 cm).
To determine the capacity of leaves of different ages to express FT, we grew Col-0 (for RNA isolation) and pFT:GUS (Takada and Goto 2003) plants for 2, 3 (pFT:GUS only), 4 or 6 weeks in SDs—conditions in which flowering is delayed and rosette leaf production is prolonged. They were moved to LD conditions 3 days prior to harvest, which is adequate time to see day-length-specific induction of FT, but before the transition to reproduction is well underway (Corbesier et al. 2007; Krzymuski et al. 2015; Kinmonth-Schultz et al. 2016), or retained in SD as a control.
Determining FT expression levels in leaves of different ages (RNA and GUS analysis)
We used analysis of FT RNA levels and pFT:GUS signal to determine the capacity of differently aged leaves to express FT. For RNA analysis: leaves of the same relative age were pooled from at least six plants. The cotyledons and first true leaves emerge in pairs, and the leaves of a pair were not separated for this analysis. Small, newly emerged leaves (1–2 mm) were also not distinguished separately, but rather harvested as a group. We isolated RNA (illustra RNAspin, GE Healthcare, Chicago, IL, USA), equalizing the isolate to ensure similar starting material across samples for RT-qPCR. We excluded any samples under 2 μg total RNA, which were primarily those of older leaves. The transcript copy number in each sample was determined using a serial dilution generated from an FT fragment spanning base pairs 1900 to 2135 from the transcriptional start site in exons 3 and 4. The fragment was amplified by RT-PCR and concentrated using ethanol purification. Fragment copy number was determined using the following equation: where Copy number = number of molecules per μL, C = concentration of the purified PCR product (g μL−1), M = molecular weight of the purified region, NA = Avogadro’s number = 6.023 × 10^23 molecules per mole (Fernández-Aparicio et al. 2013). The concentration was determined using a nanodrop (NanoDrop Lite, Thermo Scientific, USA), and then diluted using an eight-step, 1:10 serial dilution. The serial dilution was run along with the plant sample during qPCR and used to develop a linear relationship between copy and cycle number. Replicates were normalized by the replicate average.
For GUS stain image analysis: at least three whole plants of each age (2, 3 or 4 weeks old) were harvested concurrently at dusk. The plants were incubated in chilled 90 % acetone for 45 min. Prior to GUS staining, we rinsed the plants in water. Next, we immersed the plants in a GUS staining solution composed of 50 mM NaPO4, pH 7.4, 2 mM X-gluc (Gold Biotechnology, St. Louis, MO, USA), 0.5 mM K3Fe[CN]6 and 0.5 mM K4Fe[CN]6. We vacuum infiltrated the plants three times for 10 min, as previously described (Sieburth and Meyerowitz 1997). We incubated the plants at 37 °C in the staining solution for 48 h. Next, to clear the tissue, we incubated the plants at 4 °C for 30 min at each step of the following series: 30 % ethanol, fixing solution (50 % ethanol, 5 % acetic acid and 3.7 % formalde-hyde in water), 80 % ethanol and 95 % ethanol. Plants remained in 95 % ethanol overnight. We then photographed the plants, in 95 % ethanol, using a dissecting scope (Leica S8APO). Plants that were too large to be captured in one image were photographed piecewise, and the images were integrated using the GNU Image Manipulation Program (GIMP) (Kimball et al. 1995). During FT expression quantification, ImageJ struggled to distinguish between the blue of the GUS staining and the unstained leaf tissue; to more precisely quantify FT expression, we used GIMP to manipulate photos by tracing any locations stained blue, so they could be detected and analysed using ImageJ software (Rasband 1997). We then used ImageJ to quantify both the total area of FT expression and the total area of each leaf. Finally, we calculated the percentage of leaf area for each leaf that displayed FT expression. We have included both the traced and untraced versions here [see Supporting Information—Fig. S6]. The results for leaves on a single plant that were the same age (i.e. cotyledons and first true leaves) were averaged to obtain a single value for the pair. Then, values for leaves of the same age were averaged across all plants within each age group (i.e. 2, 3 or 4 weeks).
Statistical analysis and experimental controls
Statistical analysis on final leaf number and flowering time for the short-term temperature experiment was done using Generalized Estimating Equation (Carey 2015) in R Statistical Computing Software (v3.1.1; R Core Team 2015), which accounts for missing values and heteroscedasticity of residuals. The Robust Z and standard error were used to calculate P-values and 95 % confidence intervals (CIs) of the difference between the means. Plants were organized into groups of four by similarity of size and leaf number then split into the four temperature treatments to avoid the confounding effects of size. These groups were accounted for in the statistical model. The date of visible bolt was recorded when the stem below the bolt head was 2 mm in length. Floral stems were removed before rosette leaves were counted as stem height differed across temperature treatments and rosette leaves were counted blindly (without knowledge of the temperature treatment) to avoid bias. The experiment was replicated twice, with ‘replicate’ also being included as an effect in the model. Normality of residuals was determined through observation of normal Quantile-Quantile plots and the Generalized ESD Many-Outlier Procedure (Rosner 1983), resulting in detection of three outliers: one in days to bolt (2d in 12 °C treatment), and two in rosette leaf number (4d in 12 °C treatment). Justification was found to remove the latter, as they were counted by a different researcher and may have included leaves produced by auxiliary meristems, no justification was found to remove the former and thus it was not removed. Student’s t-tests (stats package, R Core Team 2015) were used to compare the leaf number of plants grown in 24 °C (control) or 12 °C temperature conditions after 2, 4 and 6 days in temperature treatments. Treatment effects were considered significant when the P-values fell below 0.05 and the CI did not contain zero. For the t-tests, P-values and CI were lowered from these values for multiple comparisons using the Bonferonni correction.
Results
Assessment of FT accumulation in FM-v1.5 across temperatures in response to gene expression or leaf growth
We began by assessing the rates of FT accumulation and the relative temperature influences of both gene expression and leaf development. We compared the total FT accumulated 9 days post emergence, equivalent to 1 week in temperature treatments, considering (i) influence of temperature on gene expression only (GE), (ii) FT accumulated with leaf tissue production as influenced by thermal time, temperature influence on gene expression excluded (LTP) and (iii) gene expression changes incorporated with leaf tissue production (LTP+GE, full FM-v1.5 model). The influence of age on a leaf’s capacity to express FT is incorporated into both the LTP and LTP+GE model variants.
When considering LTP+GE, total FT declined relative to the 22 °C-constant control, with increasing exposure times to cool temperature as would be expected from leaf area changes (Fig. 4A). When only transcriptional changes were considered (GE), FT accumulated at a faster rate than the control for some treatments (i.e. a drop in daytime temperature, Fig. 4B). For treatments in which FT accumulated more slowly than the control, as in 12 °C-constant, the relative difference from the control was less extreme than in LTP+GE. For comparison, we explored the relative difference in accumulated MPTUs, which control flowering time in FM-v1.0, over this time frame. MPTUs across treatments differed to a lesser degree than accumulated FT transcript in LTP+GE, even when nighttime temperatures carried the same weight as daytime temperatures (Fig. 4A).
Figure 4.
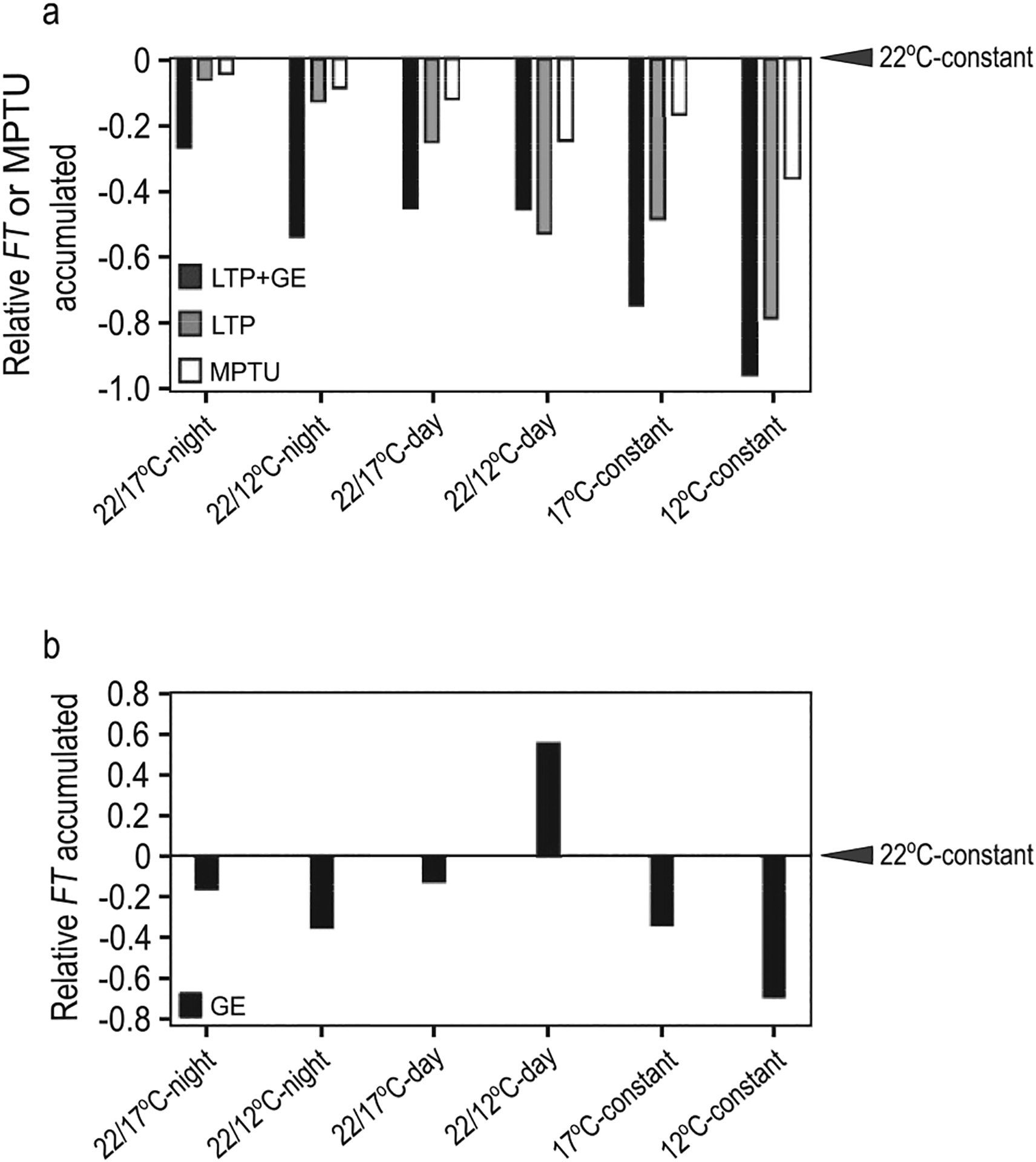
(A, B) Whole-plant FT accumulation influenced by temperature in changing and constant cool-temperature conditions, differs more strongly from the 22 °C control than does accumulated MPTUs. Total FT accumulated in constant and changing temperature conditions relative to 22 °C constant temperatures (indicated by arrowheads) 9 days post emergence, equivalent to 1 week in changing temperature treatments. (A) LTP+GE: FT accumulation in full FM-v1.5 model, i.e. temperature affects FT gene expression though CO and SVP/FLM as well as through leaf tissue production; LTP: FT accumulation only with leaf tissue production as influenced by temperature, temperature influence on FT gene expression excluded; MPTU: accumulated Modified Photothermal Units from FM-v1.0. Here, daytime and nighttime temperatures are given equal weight. (B) GE: FT accumulation considering only influence of temperature on FT gene expression, decoupled from leaf production. 22/12 or 17 °C-night indicates warm-day, cool, night cycles, 22/12 or 17 °C-day indicates treatments in which the temperature drop occurred at dawn, then remained cool for the duration of the experiment, constant indicates temperatures remained constant from seed.
To assess the influence FT transcriptional changes due to temperature have on whole-plant FT levels, we used the LTP model variant, meaning that temperature influenced FT only through leaf production modulated by thermal time and did not affect FT gene expression levels. Total FT accumulation in the warm-day, cool-night temperature-cycle treatments was higher in the LTP variant than the LTP+GE variant although it was still lower than the FT accumulated in the constant-temperature control as leaf production and expansion was slower (Fig. 4A). When the daytime temperature dropped from 22 °C to 12 °C (22/12 °C-day) FT accumulated more quickly in LTP+GE than in LTP. Taken together, we find that whole-plant FT (LTP variant) accumulates in a manner like that of thermal time, in that its rate of accumulation is altered in response to temperature. Incorporating temperature influence on FT gene expression (LTP+GE) can accelerate or decelerate whole-plant FT accumulation depending on the type of temperature fluctuations experienced.
Assessing capacity of FT accumulated to a threshold in FM-v1.5 to predict flowering
We next asked how well FT accumulation could predict flowering, and whether incorporating temperature influence through transcriptional control of FT improved model predictions when there is a temporal shift in temperature regime. To assess this, we simulated experiments for plants grown in warm-day, cool-night temperature cycles (Kinmonth-Schultz et al. 2016) as plants often experience such temperature fluctuations in nature.
We then compared the predicted final leaf number and days to bolt for warm-day, cool-night temperature-cycle treatments in the LTP and LTP+GE model variants in FM-v1.5. Cool temperatures delay bolting and increase leaf number (Blázquez et al. 2003; Kinmonth-Schultz et al. 2016). In LTP, we expected that cool nighttime temperatures would cause flowering to occur at the same leaf number as the 22 °C-constant control because temperature was not influencing gene expression, but plants would still flower later due to slower whole-plant FT accumulation through slower leaf growth. Instead, LTP predicted a leaf number trend opposite to that observed, with a lower leaf number for both 22/17 °C-night and 22/12 °C-night treatments than the 22 °C-constant control (Table 1; Fig. 5B). This behaviour was because leaves that are present in our model continued to produce FT such that it continued to accumulate over time as well as with leaf growth. Because leaf production in cooler temperatures was slower, this caused FT to reach the threshold at a leaf number lower than the control, rather than the same as the control as we had initially expected. However, as expected, both 22/17 °C-night and 22/12 °C-night treatments bolted later than the 22 °C-constant control (Table 1). The full LTP+GE variant followed a trend close to what we had observed experimentally, increasing the final leaf number for both cool-night temperature treatments and causing a stronger delay in days to bolt than LTP (Table 1; Fig. 5A–C).
Table 1.
Observed and simulated days to bolt and leaf number in Columbia-0 (Col-0) and Landsberg erecta (Ler) plants exposed to drops in nighttime temperature.
| Strain | Treatment | Obs. data | FM-v1.0 | FM-v1.5 LTP+GE | FM-v1.5 LTP | |
|---|---|---|---|---|---|---|
| Col-0 | Days to bolt | 22 °C day 22 °C night | 32.27 | 30.33 | 35.00 | 35.00 |
| 22 °C day 17 °C night | 38.60 | 30.63 | 38.50 | 35.96 | ||
| 22 °C day 12 °C night | 40.08 | 31.25 | 44.88 | 37.50 | ||
| Leaf number | 22 °C day 22 °C night | 14.77 | 18.00 | 15.00 | 15.00 | |
| 22 °C day 17 °C night | 20.50 | 16.00 | 17.00 | 13.00 | ||
| 22 °C day 12 °C night | 20.79 | 14.00 | 22.00 | 13.00 | ||
| Ler | Days to bolt | 22 °C day 22 °C night | 27.13 | 27.75 | 25.42 | 25.42 |
| 22 °C day 17 °C night | 32.75 | 28.29 | 26.50 | 25.67 | ||
| 22 °C day 12 °C night | 33.23 | 28.63 | 29.33 | 25.79 | ||
| Leaf numbers | 22 °C day 22 °C night | 7.40 | 14.00 | 8.00 | 8.00 | |
| 22 °C day 17 °C night | 8.17 | 13.00 | 8.00 | 7.00 | ||
| 22 °C day 12 °C night | 9.98 | 12.00 | 9.00 | 7.00 |
We compared this behaviour to flowering predicted using MPTU accumulation by FM-v1.0, adjusting the MPTU threshold to our LD 22 °C-constant conditions, as is recommended when using FM-v1.0 (Chew et al. 2014). If FM-v1.0 adequately captured temperature influence, then the MPTU threshold should be similar across treatments, with negligible differences between predicted and observed results for all three temperature regimes. FM-v1.0 predicted fewer leaves in both 22/12 °C-night and 22/17 °C-night conditions than in the 22 °C-constant control, because it reached the MPTU target before reaching the observed final leaf number (Table 1; Fig. 5B) in a manner similar to the behaviour of the FM-v1.5 LTP variant described above. FM-v1.0 accurately captured days to bolt for Col-0 and Ler grown in 22 °C-constant conditions and showed an expected delay in days to bolt for both 22/12 °C-night and 22/17 °C-night. However, the delay before bolting was shorter than observed (Table 1; Fig. 5D). Recalibrating to equalize the influence of nighttime and daytime temperatures (daytime temperatures are given more weight in FM-v1.0 (Chew et al. 2012)) reduced but did not eliminate these trends (Tables 1 and 2; Fig. 5E and F). Therefore, FT accumulation can be used to predict flowering and incorporating temperature influence on FT transcriptional control improved model predictions in warm-day, cool-night conditions (Table 2).
Table 2.
Fit of FM-v1.0 and FM-v1.5 for Col-0 and Ler combined.
| FM-v1.0 | FM-v1.0 (Night = Day) | FM-v1.5 LTP+GE | ||
|---|---|---|---|---|
| Days to bolt | RMSE | 5.65 | 3.69 | 3.95 |
| Bias | −4.30 | −2.69 | 0.11 | |
| Leaf number | RMSE | 5.56 | 4.91 | 2.67 |
| Bias | 0.79 | 2.33 | −0.07 |
Ability of FT accumulation to predict flowering after long-term exposure to cool temperature
As later produced leaves may lose the capacity to express FT (Fig. 3), we wondered how this would impact FT accumulation and flowering over longer developmental time periods, such as in cool constant temperatures when FT is suppressed and Arabidopsis flowers at a higher leaf number (Blázquez et al. 2003). We grew Col-0 at 12 °C-constant from seed or in 22/12 °C-day conditions. In the latter treatment, plants germinated and grew for 1 week at 22 °C then remained at 12 °C. Although a boost in FT through CO is observed in the short term in these conditions, the effect disappears with time [see Supporting Information—Fig. S3b]. We observed flowering at 24 and 28 leaves, respectively, and at 60 and 61 days after plants were moved from cold stratification to growth temperature conditions. In the full FM-v1.5 LTP+GE variant, FT failed to accumulate to the threshold set in 22 °C-constant conditions (Fig. 6). After removing the effect of leaf age from the LTP+GE model variant (i.e. equation (3.1) becameFTleaf = LA · FT, all other components remained the same), FT attained the threshold in 22/12 °C-day conditions, but not in 12 °C-constant conditions [see Supporting Information—Fig. S10]. Therefore, whole-plant FT accumulation, as influenced by leaf age, leaf tissue production and transcriptional regulation of FT by temperature may not be sufficient to predict flowering in conditions in which FT is strongly suppressed under the assumption of a constant FT threshold.
Influence of short-term drops in temperature on flowering through FT accumulation
Although long-term exposure to cool temperatures suppressed whole-plant FT and delayed flowering, rapid temperature drops at dawn in LDs (22/12 °C-day or 22/17 °C-day) caused short-term FT induction, even though the temperature then remained cool (Kinmonth-Schultz et al. 2016). As FT transcript must accumulate over several days before flowering can occur (Krzymuski et al. 2015), we wondered whether a rapid temperature drop, causing FT induction, could complement FT produced in subsequent warm temperatures to accelerate flowering, or if slower whole-plant FT accumulation with slower leaf growth, caused by the time in cool temperatures, would delay flowering. To compare the predicted influence of FT induction by temperature drops, we used the FM-v1.5 LTP+GE and LTP variants to simulate 2-week-old plants moved to 12 °C in LDs for 2, 4 or 6 days (12 °C-2d, -4d or -6d), then moved to warm, LD conditions. We also grew plants in these conditions. Control plants were moved directly to warm, LD conditions at 2 weeks.
Simulating these conditions in the full LTP+GE variant of FM-v1.5, we found little difference in days to bolt between 12 °C-2d and the control and a 3-day difference between 12 °C-6d and the control. There was a decline in leaf number from 15 leaves in the control to 14 leaves in plants exposed to 12 °C-2d and 12 °C-4d, indicating flowering at a slightly younger developmental age that translated to little difference in days to bolt between the control and 12 °C-2d. In 12 °C-6d, the leaf number increased again to be like the control. In the LTP variant, the leaf number of all three treatments was the same as the control, whereas there was an increase in days to bolt for each consecutive 2 days at 12 °C, consistent with slowed accumulation of FT due to slower leaf growth.
We observed slowed growth (relative to the control) in the cool-temperature treatments. Visible leaf number was significantly lower after 4 and 6 days in 12 °C (Fig. 7A). On Day 7, after completion of all cool-temperature treatments, there was a gradient in leaf area across treatments, with plants from 12 °C-6d being the smallest (Fig. 7B; see Supporting Information—Fig. S11). We observed a statistically significant delay in the number of days to visible bolt in both 12 °C-4d and 12 °C-6d, like both simulations (P < 0.001, Table 3; Fig. 7C). While we did not observe a significant difference in leaf number in either 12 °C-2d or 12 °C-4d relative to the control, plants in 12 °C-6d produced approximately 1.5 more leaves before flowering than the other three treatments (P < 0.001), more like the predicted increase in leaf number from 12 °C-2d and 12 °C-4d to 12 °C-6d in the LTP+GE model variant (Table 3). Combining both the simulated and observed results, it appears that the boost in FT that occurred in 12 °C-2d or 12 °C-4d conditions seems to have compensated for the slightly slower whole-plant FT accumulation in those conditions, causing plants in those conditions to bolt at a similar developmental stage (leaf number) as the control. However, because growth was slowed in those conditions, plants in 12 °C-4d bolted later in terms of number of days. In the 12 °C-6d conditions, the early boost in FT faded over time and was not enough to compensate for the overall slower whole-plant FT accumulation due to slowed growth. Therefore, plants in these conditions bolted both at a later developmental stage (higher leaf number) and at a higher number of days.
Table 3.
Flowering times in plants shifted from warm (24 °C) temperature conditions to, and remaining in, cool-temperature conditions (12 °C) for 2, 4 or 6 days.
| Treatment | Obs. data | n | Robust SE | Robust Z | P-valuea | CI of dif. (lower)a | CI of dif. (upper)a | FM-v1.5 LTP+GE | FM-v1.5 LTP | |
|---|---|---|---|---|---|---|---|---|---|---|
| Days to bolt | LD24C (int) | 35.00 | 11 | 0.62 | 31.10 | 34.75 | 34.75 | |||
| 12C, 2d | 36.00 | 15 | 0.60 | 1.73 | 0.08 | −0.65 | 2.73 | 34.92 | 35.75 | |
| 12C, 4d | 37.31 | 14 | 0.42 | 5.54 | 0.00 | 0.87 | 3.80 | 35.83 | 36.62 | |
| 12C, 6d | 38.64 | 14 | 0.35 | 7.85 | 0.00 | 2.24 | 5.02 | 37.79 | 37.58 | |
| Leaf number | LD24C (int) | 13.73 | 11 | 0.52 | 19.59 | 15.00 | 15.00 | |||
| 12C, 2d | 13.13 | 15 | 0.34 | −1.21 | 0.23 | −0.81 | 1.65 | 14.00 | 15.00 | |
| 12C, 4d | 13.64 | 14 | 0.36 | 0.49 | 0.63 | −1.07 | 1.42 | 14.00 | 15.00 | |
| 12C, 6d | 15.14 | 14 | 0.39 | 3.47 | 0.00 | 0.08 | 2.64 | 15.00 | 15.00 |
Observed and simulated days to bolt and leaf number of rosette leaves on the main stem in Columbia plants exposed to short-term drops to 12 °C temperature relative to plants remaining in the warm temperature control (24 °C) in long days (LD).
Observed treatments counted significantly different from the control when P < 0.05 and the CI of the difference from the control does not contain zero, both were lowered from these values using the Bonferonni correction to account for multiple comparisons.
Discussion
To explore the mechanisms underlying the long-observed thermal time responses, we set out to address whether accumulation of FT as a function of leaf growth as influenced by temperature could be used to predict flowering times in a manner like thermal time. Here, we found that the FM-v1.0 model using thermal time (MPTUs) and our FM-v1.5 LTP variant, in which FT accumulated only with leaf growth as influenced by temperature behaved similarly (Table 1; Fig. 5B and D), each predicting delays in days to bolt under temporal shifts in temperature regimes in LDs relative to the constant-temperature control. This indicates that accumulation of the FT gene product with leaf tissue production could be a component of thermal time. However, the delays in warm-day, cool-night conditions for each model were less than observed. The second question we addressed was whether incorporating direct temperature influence on FT could improve model predictions when there are temporal shifts in temperature regimes. Indeed, adding direct temperature regulation of FT improved model predictions by increasing the degree of predicted difference between the warm-day, cool-night treatments and the control. This suggests that incorporating underlying molecular mechanisms into models of plant development could improve model utility for a range of conditions without requiring recalibration (White 2009; Boote et al. 2013; Chew et al. 2017).
Our work additionally suggests avenues for future study to help us better understand how the external environment acts to influence underlying molecular components to yield developmental phenotypes. We found that FT was reduced in later-produced leaves (Fig. 3). This change in FT expression with developmental age was incorporated into FM-v1.5 using leaf age as a proxy and caused FT to fail to accumulate to a preset threshold to predict flowering in constant cool temperatures. This finding enables integration of qualitative (presence/absence) and quantitative (dosage response) aspects of FT effects on flowering and has implications for other conditions in which FT is suppressed, such as in short day lengths. It can help us quantify when FT plays a role during development, when FT alone is a poor predictor of flowering, and when it may act synergistically or competitively with other flowering factors.
For instance, the FT threshold requirement should be influenced by shoot-apex genes, and their sensitivity likely changes with climate and developmental age. For example, SVP acts both in the leaves to regulate FT and at the shoot apex to regulate SUPPRESSOR OF OVEREXPRESSION OF CONSTANS (SOC1). Currently, the latter mechanism is not captured in our model. In short days, high temperatures may reduce SVP activity at the shoot apex to initiate flowering despite lower FT levels (Fernández et al. 2016). At the shoot apex, SVP suppresses SOC1, which is positively regulated by FT, and which activates LEAFY (LFY), a key player in the floral transition (Schmid et al. 2003; Lee et al. 2008; Jang et al. 2009). FT protein also activates APETALA1 (AP1) at the shoot apex (Lee and Lee 2010). AP1, in turn, is involved in the down-regulation of TERMINAL FLOWER 1 (TFL1), a FT homolog. TFL1 is thought to compete with FT for binding with FD to suppress LFY and AP1, forming a negative feedback loop (Kaufmann et al. 2010; Wickland and Hanzawa 2015). Both the decrease in SVP and TFL1 would likely decrease the FT threshold needed to induce flowering. Like SVP, TFL1 may be temperature sensitive (Kim et al. 2013).
A changing threshold, due to different LATE FLOWERING alleles in Pea, a homologue of TFL1 in Arabidopsis (Foucher et al. 2003), aided flowering time predictions (Wenden et al. 2009). Incorporating such a mechanism—influenced by climate and developmental age—may aid understanding of how climate influences flowering. As proof of concept, we caused the FT threshold level to change with developmental age (thermal time) (Fig. 6). Doing so improved the predictive capacity of FM-v1.5 in constant, cool temperatures, and could be used to incorporate the action of SVP and other players at the shoot apex.
SVP, in conjunction with FLM, suppresses FT in response to cool temperatures (Blázquez et al. 2003; Lee et al. 2007, 2013). We demonstrated that residual SVP and FLM activity after short-term cold exposures could be important for FT regulation. For instance, to mimic observed dusk suppression of FT in warm-day, cool-night temperature cycles, simulated SVP/FLM activity decayed slowly after at 12 °C night, such that it was higher after 16 h at 22 °C, than it was in constant 22 °C conditions.
Our model also highlights the need to clarify the degree of temperature influence in FT activation and suppression at a range of temperatures. For example, in FM-v1.5, FT is not induced to observed levels, and induction is not maintained as long, after dawn exposure to 17 °C (Fig. 2E). It is possible that SVP activation is lower in 17 °C, than predicted from our model. Despite this, the relative difference in transcript levels across treatments was similar to the relative difference in daytime FT expression, which correlates strongly with flowering (Krzymuski et al. 2015; Kinmonth-Schultz et al. 2016) enabling FM-v1.5 to be useful in exploring FT accumulation and its influence on flowering.
Our simulations, while requiring validation in other temperature conditions, are consistent with approaches that use day length and vernalization to influence the leaf number at which the reproductive transition occurs (Brown et al. 2013). However, our work demonstrates that ambient temperature should be incorporated to influence leaf number as well, not only developmental rate. For instance, we altered FT accumulation, either by removing temperature influence on FT transcription (FM-v1.5 LTP, Fig. 4; Table 2) or by short-term, cool-temperature exposure (Fig. 2A; Table 3), affecting final leaf number. In each instance, FT still accumulated with leaf production as influenced by temperature, demonstrating that temperature influences when (in days) the reproductive transition occurs by influencing the developmental rate and whole-plant FT accumulation. We further suggest that tissue accumulation through growth is an underlying factor in the accumulation of thermal time as it causes gene products to accumulate. Together, this work demonstrates that decomposing the influences of climate and development can improve our understanding of plant responses in a range of conditions.
Supplementary Material
Appendix S1. Equation used in FM-v1.0 to describe FT transcription as a function of CO protein (Chew et al. 2014).
Table S1. Coefficients and values for equations used in FM-v1.5.
Figure S1. Graphic representation of FM-v1.0.
Figure S2. SVP/FLM activity declines over time.
Figure S3. Behavior of CO mRNA in response to different temperature regimes.
Figure S4. Simulated expression profile of LHY, plotted over time used to increase morning transcriptional sensitivity of FT.
Figure S5. Simulated FT expression profile in FM-v1.5 in the svp mutant mimics the pattern but not relative amplitude of that observed.
Figure S6. The spatial expression profile of FT changes with leaf age.
Figure S7. Behaviour of morphological and physiological parameters in FM-v1.0 and v1.5.
Figure S8. Specific leaf area (SLA) declines after growth in cool constant temperatures or in warm-day, cool-night temperature cycles relative to a constant, warm-temperature control. (Pyl et al. 2012).
Figure S9. FT expression in plants grown from seed at constant cool temperatures or moved to constant cool temperatures at dawn after 1 week in 22 °C.
Figure S10. In cool-temperature conditions, in which FT expression is suppressed, FT accumulation reaches a threshold set in 22 °C-constant conditions only after the influence of leaf age on capacity of different leaves to express FT is removed from the model.
Figure S11. Growth is slowed in plants exposed to 12 °C for 2, 4 or 6 days.
Acknowledgements
Many thanks the Jennifer Nemhauser lab for use of their dissecting scope and to Paul Panipinto for help on this project.
Sources of Funding
This work was supported in part by a Cooperative Research Program for Agricultural Science and Technology Development (PJ0127872017), Rural Development Administration, Republic of Korea and a Specific Cooperative Agreement (58-8042-6-097) between University of Washington and USDA-ARS to S.-H.K; by National Institute of Health grant (R01GM079712), National Science Foundation grant (IOS-1656076), and Next-Generation BioGreen 21 Program (SSAC, PJ013386, Rural Development Administration, Republic of Korea) to T.I.; by Biotechnology and Biological Sciences Research Council awards (BB/L026996, BB/N012348) to A.J.M.; and by the University of Washington Biology Department Frye-Hotson-Rigg Fellowship and the National Institute of Health Institutional Research and Academic Career Development Award (K12GM63651) to H.A.K.-S.
Footnotes
Conflict of Interest
None declared.
Literature Cited
- Abe M, Kobayashi Y, Yamamoto S, Daimon Y, Yamaguchi A, Ikeda Y, Ichinoki H, Notaguchi M, Goto K, Araki T. 2005. FD, a bZIP protein mediating signals from the floral pathway integrator FT at the shoot apex. Science 309:1052–1056. [DOI] [PubMed] [Google Scholar]
- Amasino R 2010. Seasonal and developmental timing of flowering. The Plant Journal 61:1001–1013. [DOI] [PubMed] [Google Scholar]
- Asseng S, Ewert F, Rosenzweig C, Jones JW, Hatfield JL, Ruane AC, Boote KJ, Thorburn PJ, Rötter RP, Cammarano D, Brisson N, Basso B, Martre P, Aggarwal PK, Angulo C, Bertuzzi P, Biernath C, Challinor AJ, Doltra J, Gayler S, Goldberg R, Grant R, Heng L, Hooker J, Hunt LA, Ingwersen J, Izaurralde RC, Kersebaum KC, Müller C, Naresh Kumar S, Nendel C, O’Leary G, Olesen JE, Osborne TM, Palosuo T, Priesack E, Ripoche D, Semenov MA, Shcherbak I, Steduto P, Stöckle C, Stratonovitch P, Streck T, Supit I, Tao F, Travasso M, Waha K, Wallach D, White JW, Williams JR, Wolf J. 2013. Uncertainty in simulating wheat yields under climate change. Nature Climate Change 3:827–832. [Google Scholar]
- Blázquez MA, Ahn JH, Weigel D. 2003. A thermosensory pathway controlling flowering time in Arabidopsis thaliana. Nature Genetics 33:168–171. [DOI] [PubMed] [Google Scholar]
- Boote KJ, Jones JW, White JW, Asseng S, Lizaso JI. 2013. Putting mechanisms into crop production models. Plant, Cell & Environment 36:1658–1672. [DOI] [PubMed] [Google Scholar]
- Bratzel F, Turck F. 2015. Molecular memories in the regulation of seasonal flowering: from competence to cessation. Genome Biology 16:192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown HE, Jamieson PD, Brooking IR, Moot DJ, Huth NI. 2013. Integration of molecular and physiological models to explain time of anthesis in wheat. Annals of Botany 112:1683–1703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carey VJ. 2015. Ported to R by Thomas Lumley (Versions 3.13 and 4.4) and Brian Ripley (Version 4.13). gee: on Solver. Version 4.13–19. [Google Scholar]
- Carter JM, Orive ME, Gerhart LM, Stern JH, Marchin RM, Nagel J, Ward JK. 2017. Warmest extreme year in U.S. history alters thermal requirements for tree phenology. Oecologia 183:1197–1210. [DOI] [PubMed] [Google Scholar]
- Chew YH, Seaton DD, Mengin V, Flis A, Mugford ST, Smith AM, Stitt M, Millar AJ. 2017. Linking circadian time to growth rate quantitatively via carbon metabolism. bioRxiv 105437. [Google Scholar]
- Chew YH, Wenden B, Flis A, Mengin V, Taylor J, Davey CL, Tindal C, Thomas H, Ougham HJ, de Reffye P, Stitt M, Williams M, Muetzelfeldt R, Halliday KJ, Millar AJ. 2014. Multiscale digital Arabidopsis predicts individual organ and whole-organism growth. Proceedings of the National Academy of Sciences of the United States of America 111:E4127–E4136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chew YH, Wilczek AM, Williams M, Welch SM, Schmitt J, Halliday KJ. 2012. An augmented Arabidopsis phenology model reveals seasonal temperature control of flowering time. The New Phytologist 194:654–665. [DOI] [PubMed] [Google Scholar]
- Christophe A, Letort V, Hummel I, Cournède P-H, Reffye P de, Lecœur J. 2008. A model-based analysis of the dynamics of carbon balance at the whole-plant level in Arabidopsis thaliana. Functional Plant Biology 35:1147–1162. [DOI] [PubMed] [Google Scholar]
- Chuine I 2000. A unified model for budburst of trees. Journal of Theoretical Biology 207:337–347. [DOI] [PubMed] [Google Scholar]
- Corbesier L, Lejeune P, Bernier G. 1998. The role of carbohydrates in the induction of flowering in Arabidopsis thaliana: comparison between the wild type and a starchless mutant. Planta 206:131–137. [DOI] [PubMed] [Google Scholar]
- Corbesier L, Vincent C, Jang S, Fornara F, Fan Q, Searle I, Giakountis A, Farrona S, Gissot L, Turnbull C, Coupland G. 2007. FT protein movement contributes to long-distance signaling in floral induction of Arabidopsis. Science 316:1030–1033. [DOI] [PubMed] [Google Scholar]
- Fernández V, Takahashi Y, Le Gourrierec J, Coupland G. 2016. Photoperiodic and thermosensory pathways interact through CONSTANS to promote flowering at high temperature under short days. The Plant Journal 86:426–440. [DOI] [PubMed] [Google Scholar]
- Fernández-Aparicio M, Huang K, Wafula EK, Honaas LA, Wickett NJ, Timko MP, Depamphilis CW, Yoder JI, Westwood JH. 2013. Application of qRT-PCR and RNA-Seq analysis for the identification of housekeeping genes useful for normalization of gene expression values during Striga hermonthica development. Molecular Biology Reports 40:3395–3407. [DOI] [PubMed] [Google Scholar]
- Foucher F, Morin J, Courtiade J, Cadioux S, Ellis N, Banfield MJ, Rameau C. 2003. DETERMINATE and LATE FLOWERING are two TERMINAL FLOWER1/CENTRORADIALIS homologs that control two distinct phases of flowering initiation and development in pea. The Plant Cell 15:2742–2754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franklin KA, Whitelam GC. 2007. Light-quality regulation of freezing tolerance in Arabidopsis thaliana. Nature Genetics 39:1410–1413. [DOI] [PubMed] [Google Scholar]
- He J, Le Gouis J, Stratonovitch P, Allard V, Gaju O, Heumez E, Orford S, Griffiths S, Snape JW, Foulkes MJ, Semenov MA, Martre P. 2012. Simulation of environmental and genotypic variations of final leaf number and anthesis date for wheat. The European Journal of Agronomy 42:22–33. [Google Scholar]
- Heinsvig Kjær K, Thorup-Kristensen K, Rosenqvist E, Mazanti Aaslyng J. 2007. Low night temperatures change whole-plant physiology and increase starch accumulation in Chrysanthemum morifolium. Journal of Horticultural Science and Biotechnology 82:867–874. [Google Scholar]
- Helliwell CA, Wood CC, Robertson M, James Peacock W, Dennis ES. 2006. The Arabidopsis thaliana FLC protein interacts directly in vivo with SOC1 and FT chromatin and is part of a high-molecular-weight protein complex. The Plant Journal 46:183–192. [DOI] [PubMed] [Google Scholar]
- Imaizumi T, Tran HG, Swartz TE, Briggs WR, Kay SA. 2003. FKF1 is essential for photoperiodic-specific light signalling in Arabidopsis. Nature 426:302–306. [DOI] [PubMed] [Google Scholar]
- Jaglo-Ottosen KR, Gilmour SJ, Zarka DG, Schabenberger O, Thomashow MF. 1998. Arabidopsis CBF1 overexpression induces COR genes and enhances freezing tolerance. Science 280:104–106. [DOI] [PubMed] [Google Scholar]
- Jamieson PD, Brooking IR, Semenov MA, Porter JR. 1998a. Making sense of wheat development: a critique of methodology. Field Crops Research 55:117–127. [Google Scholar]
- Jamieson PD, Semenov MA, Brooking IR, Francis GS. 1998b. Sirius: a mechanistic model of wheat response to environmental variation. The European Journal of Agronomy 8:161–179. [Google Scholar]
- Jang S, Torti S, Coupland G. 2009. Genetic and spatial interactions between FT, TSF and SVP during the early stages of floral induction in Arabidopsis. The Plant Journal 60:614–625. [DOI] [PubMed] [Google Scholar]
- Jones JW, Hoogenboom G, Porter CH, Boote KJ, Batchelor WD, Hunt LA, Wilkens PW, Singh U, Gijsman AJ, Ritchie JT. 2003. The DSSAT cropping system model. The European Journal of Agronomy 18:235–265. [Google Scholar]
- Karsai I, Igartua E, Casas AM, Kiss T, Soos V, Balla K, Bedo Z, Veisz O. 2013. Developmental patterns of a large set of barley (Hordeum vulgare) cultivars in response to ambient temperature. Annals of Applied Biology 162:309–323. [Google Scholar]
- Karsai I, Szucs P, Koszegi B, Hayes PM, Casas A, Bedo Z, Veisz O. 2008. Effects of photo and thermo cycles on flowering time in barley: a genetical phenomics approach. Journal of Experimental Botany 59:2707–2715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufmann K, Wellmer F, Muiño JM, Ferrier T, Wuest SE, Kumar V, Serrano-Mislata A, Madueño F, Krajewski P, Meyerowitz EM, Angenent GC, Riechmann JL. 2010. Orchestration of floral initiation by APETALA1. Science 328:85–89. [DOI] [PubMed] [Google Scholar]
- Kim W, Park TI, Yoo SJ, Jun AR, Ahn JH. 2013. Generation and analysis of a complete mutant set for the Arabidopsis FT/TFL1 family shows specific effects on thermo-sensitive flowering regulation. Journal of Experimental Botany 64:1715–1729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S-H, Yang Y, Timlin DJ, Fleisher DH, Dathe A, Reddy VR, Staver K. 2012. Modeling temperature responses of leaf growth, development, and biomass in maize with MAIZSIM. Agronomy Journal 104:1523–1537. [Google Scholar]
- Kimball S, Mattis P; The GIMP Development Team. 1995. GNU Image Manipulation Program (GIMP) [Internet]. www.gimp.org (15 February 2016).
- Kinmonth-Schultz HA, Tong X, Lee J, Song YH, Ito S, Kim SH, Imaizumi T. 2016. Cool night-time temperatures induce the expression of CONSTANS and FLOWERING LOCUS T to regulate flowering in Arabidopsis. The New Phytologist 211:208–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiss T, Dixon LE, Soltész A, Bányai J, Mayer M, Balla K, Allard V, Galiba G, Slafer GA, Griffiths S, Veisz O, Karsai I. 2017. Effects of ambient temperature in association with photoperiod on phenology and on the expressions of major plant developmental genes in wheat (Triticum aestivum L.). Plant, Cell & Environment 40:1629–1642. [DOI] [PubMed] [Google Scholar]
- Krzymuski M, Andrés F, Cagnola JI, Jang S, Yanovsky MJ, Coupland G, Casal JJ. 2015. The dynamics of FLOWERING LOCUS T expression encodes long-day information. The Plant Journal 83:952–961. [DOI] [PubMed] [Google Scholar]
- Kumudini S, Andrade FH, Boote KJ, Brown GA, Dzotsi KA, Edmeades GO, Gocken T, Goodwin M, Halter AL, Hammer GL, Hatfield JL, Jones JW, Kemanian AR, Kim S-H, Kiniry J, Lizaso JI, Nendel C, Nielsen RL, Parent B, Stöckle CO, Tardieu F, Thomison PR, Timlin DJ, Vyn TJ, Wallach D, Yang HS, Tollenaar M. 2014. Predicting maize phenology: Intercomparison of functions for developmental response to temperature. Agronomy Journal 106:2087–2097. [Google Scholar]
- Lee J, Lee I. 2010. Regulation and function of SOC1, a flowering pathway integrator. Journal of Experimental Botany 61:2247–2254. [DOI] [PubMed] [Google Scholar]
- Lee J, Oh M, Park H, Lee I. 2008. SOC1 translocated to the nucleus by interaction with AGL24 directly regulates LEAFY. The Plant Journal 55:832–843. [DOI] [PubMed] [Google Scholar]
- Lee JH, Ryu HS, Chung KS, Posé D, Kim S, Schmid M, Ahn JH. 2013. Regulation of temperature-responsive flowering by MADS-box transcription factor repressors. Science 342:628–632. [DOI] [PubMed] [Google Scholar]
- Lee JH, Yoo SJ, Park SH, Hwang I, Lee JS, Ahn JH. 2007. Role of SVP in the control of flowering time by ambient temperature in Arabidopsis. Genes & Development 21:397–402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehenbauer PA. 1914. Growth of maize seedlings in relation to temperature. Physiological Research 1:247–288. [Google Scholar]
- Lutz U, Posé D, Pfeifer M, Gundlach H, Hagmann J, Wang C, Weigel D, Mayer KF, Schmid M, Schwechheimer C. 2015. Modulation of ambient temperature-dependent flowering in Arabidopsis thaliana by natural variation of FLOWERING LOCUS M. PLoS Genetics 11:e1005588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makowski D, Asseng S, Ewert F, Bassu S, Durand JL, Li T, Martre P, Adam M, Aggarwal PK, Angulo C, Baron C, Basso B, Bertuzzi P, Biernath C, Boogaard H, Boote KJ, Bouman B, Bregaglio S, Brisson N, Buis S, Cammarano D, Challinor AJ, Confalonieri R, Conijn JG, Corbeels M, Deryng D, De Sanctis G, Doltra J, Fumoto T, Gaydon D, Gayler S, Goldberg R, Grant RF, Grassini P, Hatfield JL, Hasegawa T, Heng L, Hoek S, Hooker J, Hunt LA, Ingwersen J, Izaurralde RC, Jongschaap REE, Jones JW, Kemanian RA, Kersebaum KC, Kim S-H, Lizaso J, Marcaida M, Mueller C, Nakagawa H, Kumar SN, Nendel C, O’Leary GJ, Olesen JE, Oriol P, Osborne TM, Palosuo T, Pravia MV, Priesack E, Ripoche D, Rosenzweig C, Ruane AC, Ruget F, Sau F, Semenov MA, Shcherbak I, Singh B, Singh U, Soo HK, Steduto P, Stoeckle C, Stratonovitch P, Streck T, Supit I, Tang L, Tao F, Teixeira EI, Thorburn P, Timlin D, Travasso M, Roetter RP, Waha K, Wallach D, White JW, Wilkens P, Williams JR, Wolf J, Yin X, Yoshida H, Zhang Z, Zhu Y. 2015. A statistical analysis of three ensembles of crop model responses to temperature and CO2 concentration. Agricultural and Forest Meteorology 214:483–493. [Google Scholar]
- Montesino-San Martin M, Olesen JE, Porter JR. 2014. A genotype, environment and management (GxExM) analysis of adaptation in winter wheat to climate change in Denmark. Agricultural and Forest Meteorology 187:1–13. [Google Scholar]
- Parent B, Turc O, Gibon Y, Stitt M, Tardieu F. 2010. Modelling temperature-compensated physiological rates, based on the co-ordination of responses to temperature of developmental processes. Journal of Experimental Botany 61:2057–2069. [DOI] [PubMed] [Google Scholar]
- Piper EL, Smit MA, Boote KJ, Jones JW. 1996. The role of daily minimum temperature in modulating the development rate to flowering in soybean. Field Crops Research 47:211–220. [Google Scholar]
- Posé D, Verhage L, Ott F, Yant L, Mathieu J, Angenent GC, Immink RG, Schmid M. 2013. Temperature-dependent regulation of flowering by antagonistic FLM variants. Nature 503:414–417. [DOI] [PubMed] [Google Scholar]
- Pyl ET, Piques M, Ivakov A, Schulze W, Ishihara H, Stitt M, Sulpice R. 2012. Metabolism and growth in Arabidopsis depend on the daytime temperature but are temperature-compensated against cool nights. The Plant Cell 24:2443–2469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. 2015. R: A language and environment for statistical computing. Veanna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- Rasband WS. 1997. ImageJ [Internet]. Bethesda, MD: U.S. National Institutes of Health. https://imagej.nih.gov/ij/ (21 January 2016). [Google Scholar]
- Rasse DP, Tocquin P. 2006. Leaf carbohydrate controls over Arabidopsis growth and response to elevated CO2: an experimentally based model. The New Phytologist 172:500–513. [DOI] [PubMed] [Google Scholar]
- Rensing L, Ruoff P. 2002. Temperature effect on entrainment, phase shifting, and amplitude of circadian clocks and its molecular bases. Chronobiology International 19:807–864. [DOI] [PubMed] [Google Scholar]
- Ritchie J, Otter S. 1985. Description and performance of CERES-Wheat. A user-oriented wheat model. US Department of Agriculture, ARS 38:159–175. [Google Scholar]
- Rosner B 1983. Percentage points for a generalized ESD many-outlier procedure. Technometrics 25:165–172. [Google Scholar]
- Salazar JD, Saithong T, Brown PE, Foreman J, Locke JC, Halliday KJ, Carré IA, Rand DA, Millar AJ. 2009. Prediction of photoperiodic regulators from quantitative gene circuit models. Cell 139:1170–1179. [DOI] [PubMed] [Google Scholar]
- Schmid M, Uhlenhaut NH, Godard F, Demar M, Bressan R, Weigel D, Lohmann JU. 2003. Dissection of floral induction pathways using global expression analysis. Development 130:6001–6012. [DOI] [PubMed] [Google Scholar]
- Schwartz C, Balasubramanian S, Warthmann N, Michael TP, Lempe J, Sureshkumar S, Kobayashi Y, Maloof JN, Borevitz JO, Chory J, Weigel D. 2009. Cis-regulatory changes at FLOWERING LOCUS T mediate natural variation in flowering responses of Arabidopsis thaliana. Genetics 183:723–732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Searle I, He Y, Turck F, Vincent C, Fornara F, Kröber S, Amasino RA, Coupland G. 2006. The transcription factor FLC confers a flowering response to vernalization by repressing meristem competence and systemic signaling in Arabidopsis. Genes & Development 20:898–912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seaton DD, Smith RW, Song YH, MacGregor DR, Stewart K, Steel G, Foreman J, Penfield S, Imaizumi T, Millar AJ, Halliday KJ. 2015. Linked circadian outputs control elongation growth and flowering in response to photoperiod and temperature. Molecular Systems Biology 11:776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segal IH. 1976. Biochemical calculations: how to solve mathematical problems in general biochemistry, 2nd edn. Canada: John Wiley and Sons. [Google Scholar]
- Sieburth LE, Meyerowitz EM. 1997. Molecular dissection of the AGAMOUS control region shows that cis elements for spatial regulation are located intragenically. The Plant Cell 9:355–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song YH, Kubota A, Kwon MS, Covington MF, Lee N, Taagen ER, Laboy Cintrón D, Hwang DY, Akiyama R, Hodge SK, Huang H, Nguyen NH, Nusinow DA, Millar AJ, Shimizu KK, Imaizumi T. 2018. Molecular basis of flowering under natural long-day conditions in Arabidopsis. Nature Plants 4:824–835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song YH, Shim JS, Kinmonth-Schultz HA, Imaizumi T. 2015. Photoperiodic flowering: time measurement mechanisms in leaves. Annual Review of Plant Biology 66:441–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sperling O, Earles JM, Secchi F, Godfrey J, Zwieniecki MA. 2015. Frost induces respiration and accelerates carbon depletion in trees. PLoS One 10:e0144124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sureshkumar S, Dent C, Seleznev A, Tasset C, Balasubramanian S. 2016. Nonsense-mediated mRNA decay modulates FLM-dependent thermosensory flowering response in Arabidopsis. Nature Plants 2:16055. [DOI] [PubMed] [Google Scholar]
- Takada S, Goto K. 2003. TERMINAL FLOWER2, an Arabidopsis homolog of HETEROCHROMATIN PROTEIN1, counteracts the activation of FLOWERING LOCUS T by CONSTANS in the vascular tissues of leaves to regulate flowering time. The Plant Cell 15:2856–2865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thines BC, Youn Y, Duarte MI, Harmon FG. 2014. The time of day effects of warm temperature on flowering time involve PIF4 and PIF5. Journal of Experimental Botany 65:1141–1151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valverde F, Mouradov A, Soppe W, Ravenscroft D, Samach A, Coupland G. 2004. Photoreceptor regulation of CONSTANS protein in photoperiodic flowering. Science 303:1003–1006. [DOI] [PubMed] [Google Scholar]
- Wang N, Wang J, Wang E, Yu Q, Shi Y, He D. 2015. Increased uncertainty in simulated maize phenology with more frequent supra-optimal temperature under climate warming. The European Journal of Agronomy 71:19–33. [Google Scholar]
- Welch SM, Roe JL, Dong Z. 2003. A genetic neural network model of flowering time control in Arabidopsis thaliana. Agronomy Journal 95:71–81. [Google Scholar]
- Wenden B, Dun EA, Hanan J, Andrieu B, Weller JL, Beveridge CA, Rameau C. 2009. Computational analysis of flowering in pea (Pisum sativum). The New Phytologist 184:153–167. [DOI] [PubMed] [Google Scholar]
- White JW. 2009. Combining ecophysiological models and genomics to decipher the GEM-to-P problem. NJAS - Wageningen Journal of Life Sciences 57:53–58. [Google Scholar]
- Wickland DP, Hanzawa Y. 2015. The FLOWERING LOCUS T/TERMINAL FLOWER 1 gene family: functional evolution and molecular mechanisms. Molecular Plant 8:983–997. [DOI] [PubMed] [Google Scholar]
- Wilczek AM, Roe JL, Knapp MC, Cooper MD, Lopez-Gallego C, Martin LJ, Muir CD, Sim S, Walker A, Anderson J, Egan JF, Moyers BT, Petipas R, Giakountis A, Charbit E, Coupland G, Welch SM, Schmitt J. 2009. Effects of genetic perturbation on seasonal life history plasticity. Science 323:930–934. [DOI] [PubMed] [Google Scholar]
- Yin X, Kropff M. 1996. The effect of temperature on leaf appearance in rice. Annals of Botany 77:215–221. [Google Scholar]
- Yin X, Kropff MJ, McLaren G, Visperas RM. 1995. A nonlinear model for crop development as a function of temperature. Agricultural and Forest Meteorology 77:1–16. [Google Scholar]
- Zavalloni C, Andresen JA, Flore JA. 2006. Phenological models of flower bud stages and fruit growth of “Montmorency” sour cherry based on growing degree-day accumulation. Journal of the American Society for Horticultural Science 131:601–607. [Google Scholar]
- Zheng B, Biddulph B, Li D, Kuchel H, Chapman S. 2013. Quantification of the effects of VRN1 and Ppd-D1 to predict spring wheat (Triticum aestivum) heading time across diverse environments. Journal of Experimental Botany 64:3747–3761. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1. Equation used in FM-v1.0 to describe FT transcription as a function of CO protein (Chew et al. 2014).
Table S1. Coefficients and values for equations used in FM-v1.5.
Figure S1. Graphic representation of FM-v1.0.
Figure S2. SVP/FLM activity declines over time.
Figure S3. Behavior of CO mRNA in response to different temperature regimes.
Figure S4. Simulated expression profile of LHY, plotted over time used to increase morning transcriptional sensitivity of FT.
Figure S5. Simulated FT expression profile in FM-v1.5 in the svp mutant mimics the pattern but not relative amplitude of that observed.
Figure S6. The spatial expression profile of FT changes with leaf age.
Figure S7. Behaviour of morphological and physiological parameters in FM-v1.0 and v1.5.
Figure S8. Specific leaf area (SLA) declines after growth in cool constant temperatures or in warm-day, cool-night temperature cycles relative to a constant, warm-temperature control. (Pyl et al. 2012).
Figure S9. FT expression in plants grown from seed at constant cool temperatures or moved to constant cool temperatures at dawn after 1 week in 22 °C.
Figure S10. In cool-temperature conditions, in which FT expression is suppressed, FT accumulation reaches a threshold set in 22 °C-constant conditions only after the influence of leaf age on capacity of different leaves to express FT is removed from the model.
Figure S11. Growth is slowed in plants exposed to 12 °C for 2, 4 or 6 days.


