Temperature Dependent Properties of the Aqueous Electron

Abstract

The temperature‐dependent properties of the aqueous electron have been extensively studied using mixed quantum‐classical simulations in a wide range of thermodynamic conditions based on one‐electron pseudopotentials. While the cavity model appears to explain most of the physical properties of the aqueous electron, only a non‐cavity model has so far been successful in accounting for the temperature dependence of the absorption spectrum. Here, we present an accurate and efficient description of the aqueous electron under various thermodynamic conditions by combining hybrid functional‐based molecular dynamics, machine learning techniques, and multiple time‐step methods. Our advanced simulations accurately describe the temperature dependence of the absorption maximum in the presence of cavity formation. Specifically, our work reveals that the red shift of the absorption maximum results from an increasing gyration radius with temperature, rather than from global density variations as previously suggested.

Ab initio molecular dynamics simulations of the aqueous electron in various thermodynamic conditions at the accuracy of hybrid functional electronic structure theory are reported. This work reveals that the red shift of the absorption maximum results from an increasing gyration radius with temperature.

Introduction

The aqueous electron ($e_{\mathrm{aq}}^{-}$ ) is the simplest condensed‐phase anion in nature, consisting of an excess electron solvated in liquid water.[ ¹ , ² , ³ ] In the early 1960s, Hart and Boag discovered $e_{\mathrm{aq}}^{-}$ through its absorption spectrum, ^[4] which is characterized by a main peak resulting from transitions between the s ground state and the p excited states. ^[2] Since then, efforts in both theory and experiment have led to a better understanding of the structural, dynamical, and electronic properties of $e_{\mathrm{aq}}^{-}$ .[ ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ , ¹² , ¹³ , ¹⁴ ] However, despite nearly a half‐century of interest in $e_{\mathrm{aq}}^{-}$ , many questions remain controversial. ^[2] In particular, the question of whether $e_{\mathrm{aq}}^{-}$ occupies a cavity has been highly debated.[ ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ ] This lack of consensus mostly originated from the use of mixed quantum‐classical simulations based on the so‐called one‐electron pseudopotential method, where the electron is treated quantum mechanically and the other interactions classically.[ ¹⁹ , ²⁰ , ²¹ , ²² , ²³ ] In more recent years, cavity formation has drawn strong support, both from molecular dynamics simulations based on more accurate electronic structure methods[ ²⁴ , ²⁵ , ²⁶ , ²⁷ , ²⁸ ] and from the measurement of partial molar volumes. ^[29]

Despite this progress, the variation of the optical absorption spectrum of $e_{\mathrm{aq}}^{-}$ with temperature has remained elusive. ^[2] More specifically, the absorption maximum E _max(T) shows a red shift of 2.4–2.8 meV K⁻¹ at constant pressure,[ ³⁰ , ³¹ ] which has not yet found a consistent explanation. A similar shift with temperature is observed at constant density,[ ³⁰ , ³¹ ] suggesting that density variations only play a minor role. Within the one‐electron pseudopotential scheme, ^[21] many theoretical attempts have been undertaken to understand the dependence of E _max upon varying thermodynamic conditions. Turi and Borgis (TB) developed a potential leading to cavity formation and giving a fair absorption spectrum.[ ¹⁹ , ²⁰ ] The TB model reproduces the experimental temperature dependence of E _max, ^[32] but this agreement was demonstrated to originate from a density effect,[ ³² , ³³ ] unlike in the experiment.[ ³⁰ , ³¹ ] A more elaborate polarizable electron‐water pseudopotential model also failed in reproducing the temperature dependence.[ ² , ³⁴ ] Subsequently, Larsen, Glover, and Schwartz (LGS) developed a noncavity model, ^[22] which was found to describe E _max(T) at fixed density in a qualitatively correct fashion, apart from the slope with temperature being overestimated by a factor larger than two. ^[33]

A more accurate description of $e_{\mathrm{aq}}^{-}$ can be achieved by describing the electronic structure within density‐functional theory. In the early 2000s, ab initio molecular dynamics (AIMD) simulations based on the generalized gradient approximation found that decreasing the density resulted in a red shift of the absorption spectrum, in qualitative agreement with the TB model.[ ³⁵ , ³⁶ ] However, it is by now well known that an accurate description of $e_{\mathrm{aq}}^{-}$ requires more advanced methods to overcome delocalization errors and to capture subtle correlations effects.[ ¹¹ , ²⁵ , ²⁶ , ²⁸ , ³⁷ ] To limit the computational cost of such methods, machine learning schemes ^[38] offer a viable strategy to simulate the quantum dynamics of $e_{\mathrm{aq}}^{-}$ with inexpensive force fields. ^[28]

Here, we combine hybrid‐functional molecular dynamics and machine learning techniques to elucidate the evolution of the adsorption spectrum of the aqueous electron with temperature. Using the energies and forces determined at the hybrid functional level, we train an inexpensive force field through a neural network. ^[38] The molecular dynamics are accelerated by a multiple timestep method.[ ³⁹ , ⁴⁰ ] The long time scale enabled by such a scheme allows us to accurately determine the dependence of the structural and electronic properties of $e_{\mathrm{aq}}^{-}$ on temperature. The present results lead to cavity formation and to a temperature dependence of the absorption maximum in agreement with experiment, thereby demonstrating the strength of the applied methodology.

Results and Discussion

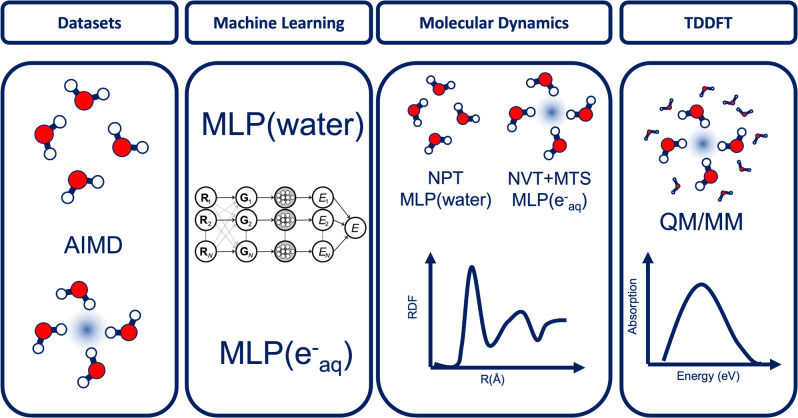
To accurately model the temperature‐dependent properties of $e_{\mathrm{aq}}^{-}$ , we combine several advanced methodologies in sequence as illustrated in Figure 1. Datasets of energies and forces are generated through advanced hybrid‐functional molecular dynamics and used to develop two machine‐learning potentials (MLPs) for simulating neat liquid water and $e_{\mathrm{aq}}^{-}$ . We adopt the neural network scheme introduced by Behler and Parrinello[ ³⁸ , ⁴¹ ] and select data set configurations according to their atomic fingerprints. ^[42] The MLP for neat water is used to perform equilibrated molecular dynamics of liquid water at constant pressure, while the MLP for $e_{\mathrm{aq}}^{-}$ is combined with a hybrid functional supplemented with nonlocal dispersion interactions ^[43] to generate molecular dynamics trajectories with a multiple time step (MTS) scheme. The employed functional provides an accurate description of the electronic structure of $e_{\mathrm{aq}}^{-}$ , ^[25] comparable to higher‐level results from perturbation theory.[ ²⁶ , ²⁸ ] In particular, this set‐up yields a Kohn–Sham band gap of 8.8 eV for liquid water ^[43] in agreement with recent bounds set for the experimental value. ^[44] In our simulations, the pressure is set at 250 bar to match the conditions in the experiment, ^[30] which take advantage of the fact that water remains in its liquid phase for a wide range of temperatures at this pressure. The MTS‐AIMD simulations are performed with the i‐PI code[ ⁴⁰ , ⁴⁵ ] interfaced with the CP2K code. ^[46] Then, the achieved structural configurations are extracted and used in quantum‐mechanics/molecular‐mechanics (QM/MM) set‐up ^[47] to calculate absorption spectra through time‐dependent density functional theory (TDDFT). A more detailed description of the employed methods is provided in the Supporting Information.

Figure 1.

Sequence of methodologies used to simulate $e_{\mathrm{aq}}^{-}$ : data set collection through ab initio molecular dynamics (AIMD); generation of machine learning potentials (MLP); multiple time step (MTS) molecular dynamics; calculation of absorption spectra through time‐dependent DFT and QM/MM.

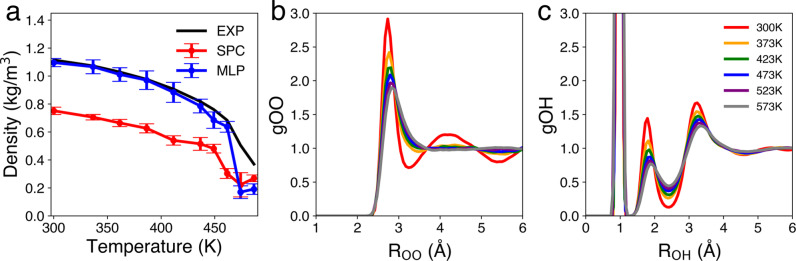
The electronic structure scheme used in our work correctly captures the temperature‐dependent density of water, whereas the simple point charge potential used in the one‐electron pseudopotential model is unable to accurately reproduce such a property. Our MLP performs well for temperatures up to about 600 K (see Figure 2a), but the description deteriorates at higher temperatures, where the low density regime (<0.6 g cm⁻³) might be affected by the lack of long‐range interactions in the MLP. Therefore, we here focus on the temperature range from 300 to 573 K. As the temperature increases, the peaks in the radial distribution functions broaden and the structure beyond the first‐neighbor shell of the water molecules is hardly perceptible (see Figures 2b and c).

Figure 2.

a) Temperature‐dependent density of water at 250 bar, as obtained experimentally (black), ^[30] with the simple point charge water model (SPC, red), and with the machine learning potential (MLP, blue). Corresponding temperature‐dependent radial distribution functions b) g _OO and c) g _OH, as obtained from the MLP‐based molecular dynamics.

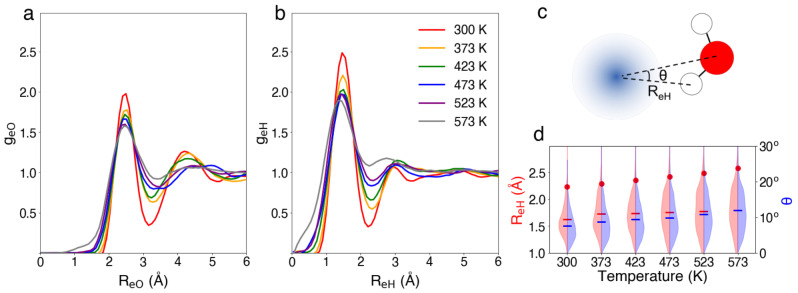
Next, we focus on the temperature‐dependent structural properties of $e_{\mathrm{aq}}^{-}$ . In Figures 3a and b, we give radial distribution functions of oxygen (g _eO) and hydrogen atoms (g _eH) with respect to the electron for various temperatures. We find that the excess electron localizes at all temperatures, forming a cavity structure. Increasing the temperature appears to accelerate the localization process, as can be seen from the evolution of the band gap and of the gyration radius (Figure S7). At all temperatures, the hydrated electron is characterized by a similar geometrical structure, with the hydrogen atoms of the nearby water molecules pointing to the center of the electron. In response to a temperature increase, the vibrational motions globally broaden the features in g _eO and g _eH. In particular, the reduction observed in correspondence of the first peaks directly relates to the cavity structure of $e_{\mathrm{aq}}^{-}$ . The temperature‐dependent structure of $e_{\mathrm{aq}}^{-}$ can be emphasized by analyzing the geometry of water molecules in the first solvation shell. In this shell, O−O and O−H correlations show a slight broadening with increasing temperature, but do not indicate any significant structural shift (see Figure S5). We also focus on two other structural features of this shell: the electron‐hydrogen distance R _eH and the angle θ characterizing the deviation from the radial alignment of the OH bond (see Figure 3c). In Figure 3d, the violin plots illustrate the distribution of R _eH and θ at various temperatures. With increasing temperatures, the distributions of R _eH and θ broaden and their mean values become higher, resulting in a larger gyration radius of $e_{\mathrm{aq}}^{-}$ (see also Figure S6).

Figure 3.

Radial distribution functions of a) O and b) H atoms with respect to the electron at various temperatures, the density being fixed at experimental values: 300 K (red), 373 K (orange), 423 K (green), 473 K (blue), 523 K (purple), and 573 K (gray); c) Graphical representation of $e_{\mathrm{aq}}^{-}$ and a neighboring water molecule defining the distance R _eH and the angle θ; d) Distribution of R _eH (red) and θ (blue) at various temperatures, where the means of the distributions are given by horizontal dashes and the average gyration radii of the electron are indicated by red dots.

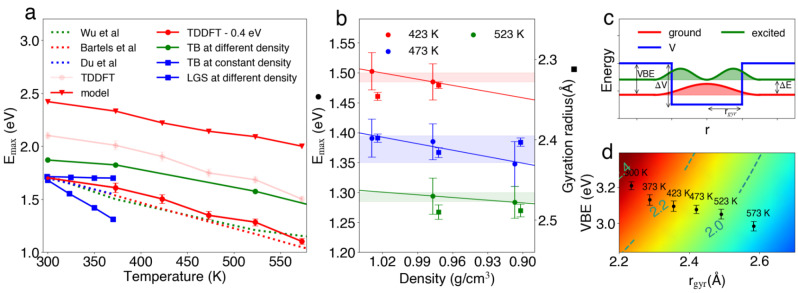
To shed light onto the temperature dependence of E _max(T), we carry out TDDFT calculations of the absorption spectrum in a QM/MM set‐up and average over the structural configurations achieved with the MTS‐AIMD simulations (see Methods). For each configuration, we consider the transitions between the ground state and the lowest five excited states. E _max is then obtained as the peak position of the convoluted absorption spectrum and mainly results from the s‐p transitions (Figure S4). We find a close to linear dependence of E _max on temperature. The calculated E _max(T) shows a substantial redshift of 2.2±0.2 meV K⁻¹ with temperature, in good agreement with experimental data (2.4 meV K⁻¹) ^[30] obtained in the same thermodynamic conditions (see Figure 4). The calculated E _max lies higher by about 0.4 eV than the experimental values. This offset should be assigned to the energy levels of the unoccupied p orbitals, which are known to sensitively depend on the adopted electronic structure method. ^[49] Indeed, at 300 K, the transition from the ground state to the vacuum level, i.e. the vertical binding energy (VBE), is found at 3.26±0.17 eV, in excellent agreement with its experimental counterpart at 3.2 eV. ^[50] The dependence of the VBE on temperature is given in Figure S10.

Figure 4.

a) Temperature dependence of $e_{\mathrm{aq}}^{-}$ absorption maximum in different thermodynamic conditions. Same color implies same thermodynamic conditions for density and temperature. Experimental data from Bartels et al. ^[30] (red dashed line), Du et al. ^[31] (green dashed line), and Wu et al. ^[48] (blue dashed line). Results from the LGS model (blue circles) and from the TB model (blue squares) at fixed water density of 0.997 g cm⁻³. ^[33] Results from the TB model (green circles) at temperature‐dependent experimental densities. ^[32] Present results as obtained (pink circles) and shifted by −0.4 eV (red). Results from the potential well model (red triangles) defined in panels (c) and (d). b) E _max values (bullets, •) and gyration radii (squares, ▪) as a function of density for different temperatures. c) One‐dimensional potential well model with ΔV being the potential depth, VBE the energy difference between the ground state and the vacuum level, ΔE the excitation energy between the ground and the first excited state, and r _gyr the gyration radius corresponding to the half‐width of the potential well. d) Contour plot showing excitation energies (in eV) obtained from the potential well model in the two‐dimensional space defined by r _gyr and VBE.

Since temperature and density vary concurrently in our simulations, the effect originating the variation of E _max remains undetermined. To clarify this issue, we carry out two additional series of simulations. In the first series, we vary the temperature (423, 473 and 523 K), while keeping the density fixed at 0.977 g cm⁻³. In the second series, various densities (1.029, 0.977 and 0.907 g cm⁻³) are considered at the same temperature of 473 K. In Figure 4b, we collect E _max obtained in these various thermodynamic conditions. It appears clearly that the temperature affects E _max more significantly than the density. At constant density, E _max redshifts with a slope of 1.9±0.4 meV K⁻¹, comparable to the slope of 2.2±0.2 meV K⁻¹ found in simulated constant‐pressure conditions (red circles in Figure 4a). In contrast, E _max redshifts only slightly with density at constant temperature. We estimate rates of 0.34, 0.36, and 0.15 eV per g cm⁻³ at 423, 473, and 523 K, respectively, in accord with the measured value of 0.2 eV per g cm⁻³. ^[51] By the same token, the structure of $e_{\mathrm{aq}}^{-}$ is more affected by the temperature than by the density, as evidenced by the radial distribution functions, the gyration radii, and the distributions of R _eH and θ (see Figures S8 and S9). In particular, the gyration radii remain almost constant upon density variations at fixed temperature, but they are highly sensitive to temperature. Overall, the gyration radius emerges as the key factor for determining E _max.

To investigate the origin of the temperature dependence of E _max, we consider a simple one‐dimensional square‐well model with finite barriers ΔV. Here, we assume the separation between the ground‐state level and the onset of the continuum to correspond to the vertical binding energy of $e_{\mathrm{aq}}^{-}$ , and the half‐width of the well to the electron gyration radius r _gyr (see Figure 4c). We numerically solve the Schrödinger equation and obtain the excitation energy ΔE to the first excited state as a function of both VBE and r _gyr (see Figure 4d). Using the values for VBE and r _gyr as obtained from our ab initio simulations (see black dots in Figure 4(d)), we obtain ΔE redshifting with temperature by 1.6 meV K⁻¹ (red triangles in Figure 4a), in reasonably good agreement with the trends seen in the experiment and in our ab initio simulations. This model implies that VBE and ΔE decrease with increasing gyration radius. Since our ab initio simulations reveal a clear increase of the gyration radius with temperature, this provides an interpretation for the temperature dependence of E _max. As a further outcome, this model puts forward the prediction that VBE decreases with temperature (Figure S10), which can be validated by future experiments.

Using the one‐electron pseudo‐potential method, the TB (green circles in Figure 4a) and the LGS model (blue circles) have been able to reproduce the experimental trend of E _max with temperature. However, these two models rely on very different underlying physical mechanisms to support the observed behavior. On the basis of the TB model, Nicolas et al. found that the variations of E _max originate from a density rather than from a temperature effect, obtaining a redshift of 1.4 eV per g cm⁻³ for increasing density and a vanishing shift for temperature variations at constant density (blue squares in Figure 4).[ ³² , ³³ ] These results are not supported by experimental observations, which measure redshifts of 0.2 eV per g cm⁻³ at constant temperature ^[51] and of 2.2 meV K⁻¹ at constant density. ^[31] The inaccuracy of the TB model could result from the underestimation of the interaction between the electron and its neighboring water molecules, as suggested by the height of the first peaks in the radial distribution functions[ ³² , ³³ ] (cf. Figure 3). At variance, the LGS model yields a temperature‐dependent structure for $e_{\mathrm{aq}}^{-}$ , which causes E _max to redshift by 5.2 meV K⁻¹ in constant‐density simulations (blue circles in Figure 4a),[ ³³ , ⁵² ] in qualitative agreement with the measured slope of 2.2 meV K⁻¹. ^[31] However, increasing evidence supporting cavity formation[ ²⁵ , ²⁶ , ²⁷ , ²⁸ , ²⁹ ] disfavors the LGS model, in which the non‐cavity structure results from an overestimated electron‐water interaction. ^[53]

Conclusions

In this work, we provide a comprehensive theoretical study of the temperature‐dependent properties of $e_{\mathrm{aq}}^{-}$ by combining accurate electronic structure calculations at the hybrid‐functional level, machine‐learning potentials, and a multiple‐time‐step scheme to achieve long timescale molecular dynamics simulations. The achieved configurations are then used in a QM/MM set‐up to obtain the absorption spectrum through TDDFT. We develop two machine‐learning potentials for describing neat water and $e_{\mathrm{aq}}^{-}$ in various thermodynamic conditions. In this way, we first simulate liquid water at a fixed pressure of 250 bar and at various temperatures, thereby providing a good description of the temperature‐dependent density of water between 300 and 573 K. Starting from the equilibrium trajectory of liquid water at various temperatures, we then address $e_{\mathrm{aq}}^{-}$ within our accelerated machine learning scheme yielding equilibrated temperature‐dependent properties. We find that the structure of $e_{\mathrm{aq}}^{-}$ is strongly affected by temperature but is less sensitive to density. Our results demonstrate that cavity‐forming electronic structure theory predicts E _max accurately under a variety of thermodynamic conditions. In particular, we reveal that higher temperature leads to larger gyration radii of $e_{\mathrm{aq}}^{-}$ , thereby causing the redshift of E _max. At last, we expect that the computational framework used here can efficiently be used for modeling excess electrons and holes in condensed phases.

Conflict of interest

The authors have no conflicts of interest to declare.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

J. Lan, V. V. Rybkin, A. Pasquarello, Angew. Chem. Int. Ed. 2022, 61, e202209398; Angew. Chem. 2022, 134, e202209398.

Data Availability Statement

The data that support the findings of this study are available in Materials Cloud (https://archive.materialscloud.org/record/2022.97).