Abstract
The overarching goal of this work is to investigate the size-dependent characteristics of the ionization potential of PbS and CdS quantum dots. The ionization potentials of quantum dots provide critical information about the energies of occupied states, which can then be used to quantify the electron-removal characteristics of quantum dots. The energy of the highest-occupied molecular orbital is used to understand electron-transfer processes when invesigating the energy-level alignment between quantum dots and electron-accepting ligands. Ionization potential is also important for investigating and interpreting electron-detachment processes induced by light (photoelectron spectra), external voltage (chemiresistance), and collision with other electrons (impact ionization). Accurate first-principles calculations of ionization potential continue to be challenging because of the computational cost associated with the construction of the frequency-dependent self-energy operator and the numerical solution of the associated Dyson equation. The computational cost becomes prohibitive as the system size increases because of the large number of 2particle-1hole (2p1h) and 1particle-2hole (1p2h) terms needed for the calculation. In this work, we present the Stratified Stochastic Enumeration of Molecular Orbitals (SSE-MO) method for efficient construction of the self-energy operator. The SSE-MO method is a real-space method and the central strategy of this method is to use stochastically enumerated sampling of molecular orbitals and molecular-orbital indices for the construction of the 2p1h and 1p2h terms. This is achieved by first constructing a composite MO-index Cartesian coordinate space followed by transformation of the frequency-dependent self-energy operator to this composite space. The evaluation of both the real and imaginary components of the self-energy operator is performed using a stratified Monte Carlo technique. The SSE-MO method was used to calculate the ionization potentials and the frequency-dependent spectral functions for a series of PbS and CdS quantum dots by solving the Dyson equation using both single-shot and iterative procedures. The ionization potentials for both PbS and CdS quantum dots were found to decrease with increasing dot size. Analysis of the frequency-dependent spectral functions revealed that for PbS quantum dots the intermediate dot size exhibited a longer relative lifetime whereas in CdS the smallest dot size had the longest relative lifetime. The results from these calculations demonstrate the efficacy of the SSE-MO method for calculating accurate ionization potentials and spectral functions of chemical systems.
1. Introduction
Ionization potential (IP) ω (or ionization energy) is defined as the energy needed to remove an electron from a chemical system.
| 1 |
| 2 |
The ejection of the electron can be facilitated using incident photons, scattering by high-energy electrons, or applying a strong electric field. As one of the fundamental properties of a material, IP has relevance to the areas of photovoltaics, mass spectrometry, photoelectron spectroscopy, electrochemistry, photocatalysis, and light-induced electron-transfer processes. The IP of atoms, molecules, and various chemical compounds is a quantity of interest when performing X-ray spectroscopy. Recently, it has been found that small gas-phase polyatomic molecules with a heavy atom, such as iodomethane, when bombarded with hard X-ray pulses display surprisingly enhanced ionization relative to an individual heavy atom with the same absorption cross-section.1 Following the excitation of an electron from an inner orbital of one atom, another electron from a higher energy orbital of the same atom can occupy this inner orbital. Instead of undergoing de-excitation, the newly excited electron can transfer energy via photon emission by ionizing an electron from an outer orbital of a neighboring atom. This process is called interatomic Coulombic decay (ICD).2,3 The IPs of both the inner and outer orbitals of molecules, dimers, and clusters influence which de-excitation mechanism occurs in a highly excited neutral or a highly excited ionized state of these types of systems. Knowledge of the IPs of these systems’ inner and outer orbitals can assist in the prediction of which de-excitation mechanism is likely to occur in a system of interest.4−9 High precision IP measurements in atoms and molecules provide important information about electron–electron correlation and serves as a benchmark for the development and testing of theories. Ionization potential also is a quantity of interest in biological systems. For example, ionizing radiation causes permanent heritable DNA damage,10 and the IPs of nucleic acid tautomers are quantities of interest, due to the role of these molecules in cancer.11
In quantum dots (QDs) and nanomaterials, knowledge of the IP for ionization from HOMO serves as an important metric for quantifying electron-transfer rates.12−18 Photoejection of electrons by X-ray and UV radiation has been used to study valence-band states in QDs.19 Cyclic voltametry has also been used to calculate HOMO energies in QDs and IPs.20 Transient photoemission in two-photon experiments has provided information on the energy levels of unoccupied orbitals.21 Knowledge of the relative positions of the HOMO and lowest unoccupied molecular orbital (LUMO) levels of a QD with respect to the surface ligands is an important factor in extraction of a hot carrier from the QD.19
In molecular quantum chemistry, the simplest approximation of IP (denoted as ωi0) is given by the Koopmans’ approximation, where the exact IP is approximated as the negative of the orbital energies.
| 3 |
Koopmans’ treatment utilizes the Hartree–Fock (HF) approximation to obtain a single N-electron Slater determinant from which an electron from one of the occupied states is annihilated, as shown in eq 3. Although Koopmans’ theorem is limited by the use of single Slater determinants and does not account for orbital relaxation and electron–electron correlation effects, it still provides an acceptable first approximation for the IP of a system of interest.22 Going beyond Koopmans’ approximation by including the effect of electron−electron correlation can be achieved in a variety of different ways such as with electron-propagator methods,23−31 algebraic diagrammatic construction (ADC),32,33 equation-of-motion coupled-cluster (IP-EOM-CCSD),34−39 many-body perturbation theory (MBPT),40,41 GW method,42 correlated-orbital theory (COT),43 and time-dependent density functional theory (TDDFT).44−46 The IP of the HOMO has a special significance in DFT because of Janak’s theorem and plays a prominent role in the development and testing of DFT functionals.47 Without loss of generality, the many-body correction to the IP can always be written as,
| 4 |
where Δωp accounts for all of the correction terms missing from the Koopmans’ approximation; post-HF methods mentioned earlier offer different approximations and formulations for calculating Δωp. However, efficient first-principles calculation of Δωp for large chemical systems continues to be challenging and is an active field of research. Using the electron-propagator method, Ortiz and co-workers developed a series of approximations that offer an order-by-order treatment of electron correlation to the many-body correction for IPs.23−25,48,49 Open-shell systems possess additional complexities compared to their closed-shell counterparts, and the spin-flip EOM-IP approach has been used to treat open-shell systems.50 In the GW formulation, the projective eigen decomposition of the dielectric screening (PDEP) algorithm has been used for calculating the quasiparticle gap of QDs.42 In recent works, methods using stochastic techniques have been demonstrated to achieve the low-scaling needed for applications to large chemical systems. Specifically, the use of stochastic orbitals in the stochastic Green’s function method developed by R. Baer can be used for the calculation of IPs.51 A different strategy of combining the Laplace-transformed expression of the self-energy operator with a real-space Monte Carlo integration scheme developed by Hirata and co-workers has been used for the calculation of IPs at the second-order MP2 level.52 The approach was recently extended for ground-state MP4 level.53 In a related work by Li et al., the Laplace-transformed MP2 approach has been combined with the density-of-states approach to reduce the overall computational cost of the MP2 calculation.54 This approach demonstrated the effectiveness of using the intrinsic degeneracies present in chemical systems to reduce the overall cost of MP2 calculations.
In this article, we present the stratified stochastic enumeration of molecular orbitals (SSE-MO) method for the efficient computation of the IP through the iterative solution of the Dyson equation. The SSE-MO method was originally inspired by the 2013 paper, “Stochastic Enumeration Method for Counting NP-Hard Problems” by Rubinstein.55 The original stochastic enumeration by Rubinstein was based on the importance sampling scheme. In the field of computer science, the stochastic enumeration technique has been applied to traversing deep tree structures and implementing backtracking algorithms.55 For the SSE-MO method, we have combined stochastic enumeration with stratified sampling to perform the necessary summations over a direct-product space of molecular orbital indices and 6D Cartesian coordinate space. The reduced computational cost of the SSE-MO method allowed us to investigate the full frequency-dependent pole structure of the 1-particle Green’s function by an iterative solution of the Dyson equation. In this work, the SSE-MO method was used to investigate IPs of PbS and CdS QDs. The motivation for the SSE-MO method comes from the fact that not all terms contribute equally to the overall self-energy operator. A similar observation has also been made for the density-of-state MP2 method.54 For example, for the Pb4S4 system, the contribution for each term as a function of the hole-index, (i), is presented in Figure 1. Without loss of generality, the self-energy operator can be written as the sum of the 2-particle 1-hole (2p1h) and 1-particle 2-hole (1p2h) terms as shown in eq 5.
| 5 |
It is seen that some terms contribute more than other terms. The SSE-MO method aims to distribute the computation effort used to calculate of the overall self-energy operator in proportion to the contribution of each of the terms and their associated errors. Here, we provide a general formulation of stratified stochastic tensor contraction (section 2.1), details about the construction of the self-energy operator (section 2.2), formulation of stochastic stratified sampling in MO space (section 2.3), performing low-discrepancy sampling (section 2.5), construction of the control-variate functions for the real-space integrals (section 2.6), performing joint MO-space real-space stratified sampling (section 2.7), the iterative solution of the Dyson equation (section 2.2), and the calculation of pole-strengths of the Green’s function and calculation of higher-order derivatives of the self-energy operator (section 2.9). Benchmark calculations on well-studied systems and new results on PbS and CdS QDs are presented in section 3. Comparisons to existing methods and future directions are discussed in section 4.
Figure 1.
Percent contribution of terms Ai2p1h and Ai (defined in eq 5) to the total self-energy as a function of hole index (i) for Pb4S4.
2. Theory
2.1. Stratified Stochastic Enumerated Tensor Contraction
As an introduction to the application of SSE for the calculation of the self-energy operator, we present the SSE approach for performing a general N-index tensor contraction. We start by considering the following general tensor contraction S = Tr{ABCD}.
| 6 |
One situation for which this type of tensor contraction is encountered is when the integration of a 4-point kernel in real space ⟨A(r1)B(r2)C(r3)D(r4) G(r1, r2, r3, r4)⟩ on a spatial grid with N point per dimension is being performed. This tensor contraction has N12 terms and a simple sequential evaluation will require N12 terms. For the stratified stochastic enumeration approach, we will first define a composite index K such that K = 1, ..., N12. The composite index, K, uniquely maps each ordered set of indices (i1, i2, i3, ..., i12) to an integer in 1, ..., N12.
| 7 |
Using the composite index K, we can define the summation as displayed in the following equation.
| 8 |
Next, we divide the entire range of K into N nonoverlapping segments Nseg = N. The number of terms in each segment is NT = N11. The summation over K can be written in terms of the segmented summation.
| 9 |
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
The partial averages are defined as follows.
| 15 |
The total sum can be written as displayed in the equation below.
| 16 |
In SSE, the sequential segment average, X̅, is approximated using the stochastic average,
| 17 |
| 18 |
| 19 |
| 20 |
where the subscript in 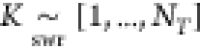 denotes
“sampling-without-replacement”.
For any segment “p”, the SSE average
approaches the sequential average as Mp → NT.
denotes
“sampling-without-replacement”.
For any segment “p”, the SSE average
approaches the sequential average as Mp → NT.
| 21 |
The SSE estimate of the total summation is presented in the equation below.
| 22 |
The allocation of the sampling points for each segment is proportional to the variance in the SSE segment average X̅pSSE.
| 23 |
| 24 |
The SSE approach is based on stratified sampling, which has been used extensively for reducing sampling error in Monte Carlo calculations56−58 and a brief description stratified sampling is presented in the Supporting Information (SI). The SSE method is not restricted to square tensors and can be applied to rectangular tensors as well. We recommend a row-major composite indexing scheme. For an index vector (i1, i2, i3, ..., iD), where D is the dimension of the tensor and each index (id, d = 1, D) is in the range (id = 1, ..., Nd), the row-major composite index K can be calculated using the following expression.
| 25 |
2.2. Second-Order Dyson Equation
In this work we are interested in calculating the IPs of chemical systems. The component of the 1-particle Green’s function, G(ω), that contains information about the IPs can be expressed in the Lehman representation as follows.59
| 26 |
where, Gpq is the matrix element of the matrix representation of the operator in canonical Hartree–Fock (HF) orbital basis {χp},
| 27 |
{ aq†, ap,} are creation and annihilation operators defined with respect to the HF orbitals, {E0, Ψ0N} are the exact ground state energies and wave function, and H is the electronic Hamiltonian. By inserting a complete set of projectors, 1 = ∑m |Ψm⟩ ⟨ΨmN–1|, we obtain the following equation.
| 28 |
As shown in eq 28, the Green’s function’s poles correspond to the vertical IPs of a many-electron system.
| 29 |
The quantity |Amp|2 is the residue of the pole and is known as the pole strength.
| 30 |
The limit η → 0+ in eq 28 is traditionally associated with this expression because of its use in performing the Fourier transform from the time-domain to frequency-domain and will be suppressed in the rest of the derivation. Analogous to the many-body Green’s function, the uncorrelated HF Green’s function G0 is given by the following expression.59
| 31 |
which immediately simplifies to following diagonal representation.59
| 32 |
where i, j = 1, Nocc are indices for occupied orbitals and ϵi is the orbital energy. The above equation recovers the Koopmans’ approximation to the IPs, which is defined as EIPKoopmans = −ϵi.
In the frequency representation, the relationship between the correlated 1-particle Green’s function, G, and the uncorrelated Green’s function G0 is given by the well-known Dyson equation.60
| 33 |
Here, Σ is the self-energy operator. The relationship between the correlated and uncorrelated Green’s function can be derived using various techniques including time-dependent perturbation theory, time-independent perturbation theory, coupled-cluster theory, the configuration interaction method, and electron-propagator methods.26,34,59,61,62 The above operator equation can also be presented in various representations such as plane-waves, real-space grids, and canonical HF orbitals.42,63,64 In this work, we use canonical HF orbitals to represent the Dyson equation.60 To facilitate the calculation of the poles, it is useful to express eq 33 in terms of inverse operators by multiplying G–1(ω) from left and G0–1(ω) from the right.
| 34 |
Once G(ω) is determined for an appropriate set of values of ω, the poles can be observed by constructing a plot of G(ω) versus ω. Approximating the total self-energy operator by diagonal representation,
| 35 |
allows for analytical inversion of the Dyson equation into the following simplified expression,60
| 36 |
where ωi0 is the orbital energy of occupied orbital (i) and ω = −EIP. We have used the second-order approximation to the self-energy operators, which in the canonical MO basis is defined as,60
 |
37 |
where i, j, and k indicate occupied spin orbitals and a and b indicate virtual spin orbitals.
Using the restricted Hartree–Fock (RHF) formulation, the correction to the orbital energies using the second-order self-energy expression can be written as,
| 38 |
where the RHF expressions for the self-energy terms are defined as,
| 39 |
| 40 |
| 41 |
| 42 |
Here, we have used the following compact notation for the energy denominators,
| 43 |
| 44 |
and the r12–1 matrix elements are defined using the chemist’s notation for the indices.
| 45 |
Next, we will develop the SSE-MO approach for evaluating the self-energy operator.
2.3. Stratified Stochastic Enumeration of Self-Energy
We begin by defining
a set  of ordered integers
(i, a, b),
of ordered integers
(i, a, b),
| 46 |
which contains all the possible combinations
of indices that occur in 2p1h self-energy expression. We will use
the composite index K = (i, a, b) to enumerate this ordered set of
integers. The size of set 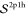 is given as,
is given as,
| 47 |
Using this notation, we can define a general form of the 2p1h self-energy term as follows.
| 48 |
where,
| 49 |
| 50 |
| 51 |
In eq 48 the summation is performed sequentially for all terms. In the stochastic enumeration (SE) approach the sequential sum is replaced by a stochastic summation. We define a new operator Σ̃ which is defined as follows,
| 52 |
and where K is sampled from
the set  . This sampling
is performed without replacement
and the notation
. This sampling
is performed without replacement
and the notation  is used to emphasize this procedure (sample-without-replacement).
The NsampleMO is sample size and bounded from above by Kmax. In the limit when the sample size approaches Kmax2p1h the
following limiting condition is satisfied.
is used to emphasize this procedure (sample-without-replacement).
The NsampleMO is sample size and bounded from above by Kmax. In the limit when the sample size approaches Kmax2p1h the
following limiting condition is satisfied.
| 53 |
Simple stochastic enumeration will involve performing the sampling over multiple runs and averaging the final results.
| 54 |
The variance is defined as follows.
| 55 |
We expect the variance to disappear when NsampleMO approaches Kmax,
| 56 |
To reduce the variance of the overall
calculations,
we introduce stratification in the sampling procedure. This is achieved
in two steps. First, the set  is decomposed
into a union of nonintersecting
subsets,
is decomposed
into a union of nonintersecting
subsets,
| 57 |
| 58 |
where the subsets are nonoverlapping.
| 59 |
The number of elements in subset M is denoted as Kmax2p1h,M.
| 60 |
In the second step, X̃2p1h is calculated using summation over all the subsets.
| 61 |
The stratified stochastic enumeration of the MO indices (SSE-MO), which uses stochastic enumeration for segment sampling, is described by the following equation.
| 62 |
To write the expressions in compact notation, we introduce the following for stochastic summation.
 |
63 |
Using this notation, we can write the following expression.
 |
64 |
A similar treatment is performed for the 1p2h terms. The combined result for the total self-energy operator is given as,
 |
65 |
2.4. Calculation of Optimal Sampling Points for MO-Space Stratified Sampling
To calculate optimal sampling points, we define the segment average as,
| 66 |
which allows us to write the following expression.
| 67 |
It is important to note that Ỹp2p1h,M is a stochastic variable for which the average value, Ỹp, can be obtained by sampling over multiple runs.
| 68 |
The variance is defined as,
| 69 |
The variance of Ỹ goes to zero as NsampleMO,M approaches Kmax,
| 70 |
To distribute the sampling points optimally, we define the following weight factor,
 |
71 |
In addition to that we also define another weight factor that depends on the magnitude of the terms,
 |
72 |
The sampling is performed in batches, and the variance is updated after completion of a batch. The number of sampling points for each segment has the general form of,
| 73 |
where all segments get Nbase sample points per batch irrespective of the segment average and variance. Nopt indicates the number of additional sample points that are distributed in a manner that is proportional to the normalized weights, which depend on the segment average and variance.
2.5. Low-Discrepancy Sampling without Replacement Using Quasi-Monte Carlo Method
It is important to note that
obtaining 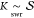 is a correlated sampling process. It is
intrinsically non-Markovian and depends on the entire history of the
string of previously generated indices. One way to achieve this in
discrete integer space is by performing self-avoiding random walks.
However, sampling in the self-avoiding random walker is local in nature,
and therefore is not ideal for variance reduction in each segment.
Here we use quasi-Monte Carlo sampling and a low-discrepancy integer
sequence to perform sampling within each segment.56−58 The linear
congruent generator for low-discrepancy quasi-random numbers is modified
for generation of integer sequences.56 The
sampling index for a segment M is defined as K(M) and can have values in
the range [1, ..., Kmax(M)]. The exact value
of Kmax for each segment is known at the start
of the calculation and is a consequence of the stratification procedure
described in subsection 2.3. Associated with each segment are two integer random numbers
which we define as q(M) and r(M). The variable q(M) impacts the discrepancy
of the points and is an integer random number chosen randomly from
the interval q(M) ∼
[10, 50]. Using q(M),
we define the following sequence from which r(M) is selected randomly.
is a correlated sampling process. It is
intrinsically non-Markovian and depends on the entire history of the
string of previously generated indices. One way to achieve this in
discrete integer space is by performing self-avoiding random walks.
However, sampling in the self-avoiding random walker is local in nature,
and therefore is not ideal for variance reduction in each segment.
Here we use quasi-Monte Carlo sampling and a low-discrepancy integer
sequence to perform sampling within each segment.56−58 The linear
congruent generator for low-discrepancy quasi-random numbers is modified
for generation of integer sequences.56 The
sampling index for a segment M is defined as K(M) and can have values in
the range [1, ..., Kmax(M)]. The exact value
of Kmax for each segment is known at the start
of the calculation and is a consequence of the stratification procedure
described in subsection 2.3. Associated with each segment are two integer random numbers
which we define as q(M) and r(M). The variable q(M) impacts the discrepancy
of the points and is an integer random number chosen randomly from
the interval q(M) ∼
[10, 50]. Using q(M),
we define the following sequence from which r(M) is selected randomly.
| 74 |
Using q(M) and r(M), the low-discrepancy sequence is defined as,
| 75 |
| 76 |
where  is the floor of the ratio.
is the floor of the ratio.
2.6. Control Variate for Monte Carlo Evaluation of Two-Electron Integrals
In this section, we extend the stochastic procedure developed in the previous section for numerical evaluation of the two-electron integrals. Monte Carlo evaluation of the two-electron integrals is not a requirement for implementing the SSE-MO method, and the SSE-MO procedure described in section 2.3 can be used whenever the two-electron repulsion integrals, Vpqst, are available in MO representation. However, for large systems, it is computationally advantageous to avoid the AO-to-MO two-electron transformation and instead, to numerically integrate directly in the MO representation using the Monte Carlo scheme.
Associated with each MO pair function, ψp(r)ψq(r), we define a control-variate function, ψpqcv(r). The control variate function must satisfy two important features. First, ψpq(r) must be nonfactorizable as a product of functions that depend only p and q indices.
| 77 |
Second, the two-electron integrals, [ψpqcv(r1)|r12|ψstcv(r2)], must be known analytically. Adding and subtracting the control variate function, we express the MO product function as follows.
| 78 |
| 79 |
Here, αpq is the control variate and dpq(r) is the difference function. Using the above expression, the two-electron integral can be expressed as,
| 80 |
where,
| 81 |
and,
| 82 |
The control variate, αpq, is defined as the quantity that minimizes the following weighted-variance function.
| 83 |
Here, Sspace is a set of sampling points in 3D space from which r is drawn at random. The control-variate functions, ψpqcv, are represented by Gaussian functions. For p = q, a single Gaussian function is used and for p ≠ q a linear combination of two Gaussian functions is used.
| 84 |
| 85 |
This form of the control variate function guarantees the orthonormality conditions for the MOs.
| 86 |
The widths and the centers of the Gaussian functions are determined using a moment-matching condition. The weighted moments for any pair of molecular orbitals are calculated as,
| 87 |
and the moments for the control-variate functions are obtained analytically.
| 88 |
The coefficients for the control-variate function are obtained by performing a steepest-descent search on the following loss-function.
| 89 |
The equations eq 83 and eq 89 completely define the control-variate function and are used to calculate the Vpqstcv term.
2.7. Monte Carlo Evaluation of Two-Electron Integrals Using Real-Space Stratified Sampling
Since Vpqstcv is analytical, only the Dpqst terms are calculated numerically using the stratified Monte Carlo procedure. We use a combination of ratio estimator, control variate, and stratified sampling techniques to efficiently and accurately evaluate the MO integrals. For calculating Dpqst, we define the following two-electron kernel function,
| 90 |
where,
| 91 |
Associated with each Dpqst integral, we define a control variate fpqstcv as,
| 92 |
where the integral of the control variate is 1 for all values of p, q, s, t.
| 93 |
The calculation of Dpqst requires evaluation of the six-dimensional integral over all space. Traditionally, Monte Carlo integration is performed over an N-dimensional unit cube by transforming the integral range from [−∞, + ∞] to [0, 1]. One approach to achieve this is by using the following transformation,
| 94 |
| 95 |
However, this procedure introduces singularity in the form of the Jacobian J(t) in the integration kernel. In this work, we use a finite-grid approximation to evaluate the integral over a finite volume,
| 96 |
where the limits selected are large enough so that ϵ ≤ 10–5 for all MOs. Using fpqstcv, we define the following ratio estimator for Monte Carlo evaluation of the Dpqst integral.
| 97 |
The averages ⟨Tpqstr12–1⟩ and ⟨fpqst⟩ are defined as follows.
| 98 |
| 99 |
We introduce stratification in the sampling of points in real-space by dividing the entire space into a set of Nsegspace nonoverlapping regions with identical volumes.
| 100 |
| 101 |
The stratified sampling estimate of the averages is then defined as,
| 102 |
Nsamplespace,M,pqst is the number of sampling points associated with the spatial segment, M for indices p, q, s, t. Similar to the stratification strategy in eq 73, the sampling points for each segment are proportional to the variance of the integral kernel in that segment.
| 103 |
| 104 |
We use common-random-number (CRN) sampling for sampling within a segment. The CRN method has been used extensively for reducing variance56−58 and a brief summary of the method is presented in ref (65). In the evaluation of the integral, this means that at any point in time, if a random number η1 is used in the evaluation of Tpqst, then that same random number is used for evaluation of fpqstcv in the same segment. To emphasize this usage, we use superscript “CRN” (common random number) in the following expression.
 |
105 |
2.8. Iterative Solution of the Dyson Equation
Combining the results from section 2.3 and section 2.7, we can express the full self-energy operator as the sum of two terms,
| 106 |
The first term Σpcv(ω) depends only on control-variate functions and is evaluated analytically.
 |
107 |
The second term contains the different terms and is defined as follows.
 |
108 |
The single-shot determination of the self-energy operator is performed by evaluating the self-energy at the HOMO energy.
| 109 |
| 110 |
The full iterative solution of the Dyson equation is obtained by evaluating Σp(ω) for a range of ω and then finding the point where,
| 111 |
The SSE-MO method allows for a third approximation for ω. We can solve the Dyson equation iteratively using Σpcv(ω)
| 112 |
and then include the correction from ΔΣp.
| 113 |
2.9. Calculation of Derivatives
The first derivative of the self-energy, with respect to ω, is useful for locating the poles of G(ω), and is defined as follows.
 |
114 |
The higher-order derivatives of the self-energy operator can then be obtained from the higher-order powers of the denominator.
| 115 |
| 116 |
In the SSE-MO method, the derivative of Σp is obtained by replacing the energy denominator with the higher powers of the denominator,
| 117 |
| 118 |
The contributions from Σpcv are obtained analytically, and the contributions from the ΔΣp are obtained from the stochastic enumeration procedure described above. Because the derivative does not impact r12, which is present in expression for the self-energy, the calculation of the derivatives can be performed concurrently while the calculation of ΔΣp is being performed. This approach was used for the construction of the spectral function and is presented in section 3.2.
2.10. Computational Details
The SSE-MO method was applied to investigate the ionzation potentials of PbS and CdS QDs. In addition, benchmark calculations for Ne, H2O, and CH4 were also performed. The single-particle states and energies were obtained from HF calculations using the 6-31G* basis for Ne, H2O, and CH4 and the LANL-2DZ ECP basis for the quantum dots. These HF calculations were performed using the TERACHEM electronic structure package. The SSE-MO calculations were performed by dividing the MO-index space into Nocc number of segments. The 6D Cartesian space was divided into 100 nonoverlapping regions. A total of Nsample ∼ 109 sampling points were used for calculating the self-energy at each value of ω and the sampling points were distributed using the stratification strategy described earlier. We used the relative standard deviation, σrel, also known as coefficient of variance for defining the convergence criteria for the calculated IPs (eq 119).
| 119 |
In this work, we enforced σrel < 10–2 to be the criteria for convergence for each segment.
3. Results
3.1. 10-Electron System
For benchmarking and testing, the SSE-MO method was used to calculate the IPs of Ne, H2O, and CH4. The results for these chemical systems are presented in Table 1. The IPs were calculated using both single-shot and iterative solution of the Dyson equation and the results between the two approaches were found to be very similar to a maximum difference of 0.17 eV. In all cases, the SSE-MO results were found to be in good agreement with the previously reported results.
Table 1. Ionization Potentials (eV) of Ten Electron Systems: Comparison with Benchmark Literature Values.
3.2. Ionization Potential of PbS and CdS Quantum Dots
The SSE-MO method was applied to Pb4S4, Pb44S44, Pb140S140, Cd6S6, Cd24S24, and Cd45S45 and the ionization potentials from the single-shot and iterative solution of the Dyson equation are presented in Table 2 and Table 3, respectively. We note that the calculated IPs are vertical ionization potentials and do not include contributions from the quantum mechanical treatment of nuclear degrees of freedom. Figure 2 illustrates the graphical verification of the self-consistency of the iterative procedure for Pb140S140. We observe that the curve for Σ(ω) + ω0 versus ω intersects with the curve for ω versus ω at that the value of ω for which the diagonal approximation to the Dyson equation converges. The frequency dependence of the 1-particle Green’s function was evaluated near the poles and is presented in Figures 3, 4, and 5.
Table 2. Self-Energy and Ionization Potentials (eV) of PbS and CdS Quantum Dots from Single-Shot Solution.
| system | Koopmans’ | self-energy from single-shot solution | IP from single-shot solution |
|---|---|---|---|
| Pb4S4 | 8.28 | 0.65 | 7.63 ± 0.05 |
| Pb44S44 | 7.13 | 0.22 | 6.91 ± 0.04 |
| Pb140S140 | 6.91 | 0.09 | 6.82 ± 0.05 |
| Cd6S6 | 5.25 | 0.42 | 4.837 ± 0.04 |
| Cd24S24 | 6.25 | 0.09 | 6.16 ± ϵ < 0.01 |
| Cd45S45 | 6.09 | 0.23 | 5.86 ± 0.02 |
Table 3. Self-Energy and Ionization Potentials (eV) of PbS and CdS Quantum Dots from Iterative Solution.
| system | Koopmans’ | self-energy from iterative solution | IP from iterative solution |
|---|---|---|---|
| Pb4S4 | 8.28 | 0.61 | 7.66 ± 0.01 |
| Pb44S44 | 7.13 | 0.17 | 6.96 ± 0.01 |
| Pb140S140 | 6.91 | 0.28 | 6.71 ± 0.08 |
| Cd6S6 | 5.25 | 0.41 | 4.84 ± 0.01 |
| Cd24S24 | 6.25 | 0.08 | 6.16 ± ϵ < 0.01 |
| Cd45S45 | 6.09 | 0.22 | 5.87 ± 0.01 |
Figure 2.

ω (ordinate) versus ω (abscissa) displayed as the curve labeled ω. The curve labeled ω0+Σ displays the relationship between the HOMO energy + the self-energy (ordinate) and ω. The value of ω at which these two curves intersect is equivalent to the value of ω for which the diagonal approximation to the Dyson equation converges.
Figure 3.

Poles of G0(ω) and G(ω) for the Pb4S4 system. G(ω) (ordinate) versus ω (abscissa) is labeled as G(ω) in the legend. The curve labeled G0(ω) displays the relationship between G0(ω) (ordinate) and ω (abscissa).
Figure 4.

Poles of G0(ω) and G(ω) for the Pb44S44 system. G(ω) (ordinate) versus ω (abscissa) is labeled as G(ω) in the legend. The curve labeled G0(ω) displays the relationship between G0(ω) (ordinate) and ω (abscissa).
Figure 5.

Poles of G0(ω) and G(ω) for the Pb140S140 system. G(ω) (ordinate) versus ω (abscissa) is labeled as G(ω) in the legend. The curve labeled G0(ω) displays the relationship between G0(ω) (ordinate) and ω (abscissa).
When compared to G0(ω), the poles of G(ω) were found to have higher values of ω indicating that for these systems, inclusion of electron correlation effects resulted in a lower IP than Koopmans’ IP values. Comparison between G and G0 shows that inclusion of electron correlation in IPs becomes more important for larger dots. Comparison between the single-shot versus iterative solution of Dyson equation also exhibits similar trends, where the need for iterative solutions become more important for larger dots.
3.3. Single-Pole Approximation to the Spectral Function
We define the single-pole approximation to the spectral function as,
| 120 |
where the subscript “sp” in Asp denotes that we are looking at the form of the spectral function near the pole (ω= ϵp). The imaginary part of the self-energy operator can be approximated from the first derivative of the self-energy, with respect to ω, as described in section 2.9. For example, the imaginary part of the following quantity I(ω),
| 121 |
is given by,
| 122 |
In Figure 6, the ratio Awp/Awpmax is plotted as a function of ω/ωopt for the three PbS QDs.
Figure 6.
Ratio Awp/Awpmax (ordinate) plotted as a function of ω/ωopt (abscissa) for a series of PbS quantum dots. Awp/Awp is the ratio of Asp(ω) and the maximum value of Asp(ω). ωopt is the value of ω for which convergence of the diagonal approximation to the Dyson equation is achieved.
The line width of the plot was found to be narrowest for the Pb4S4 and broadest for Pb44S44. This feature indicates that the relative lifetime of the quasi-hole in the intermediate dot size (Pb44S44) is longer than the other dots in the series. Similar analysis for the CdS QDs in Figure 7 revealed that the line width decreases with increasing dot size. The results from the spectral analysis highlight the importance of including frequency dependency in the self-energy operator. The plots also demonstrate the impact of many-body correlations in the these systems. Specifically, in the absence of electron–electron correlation, the limit σ → 0 will reduce the plots to a Dirac delta function.
Figure 7.
Ratio Awp/Awpmax (ordinate) plotted as a function of ω/ωopt (abscissa) for a series of CdS quantum dots. Awp/Awp is the ratio of Asp(ω) and the maximum value of Asp(ω). ωopt is the value of ω for which convergence of the diagonal approximation to the Dyson equation is achieved.
4. Discussion
4.1. Correlated Sampling in the Combined Cartesian and Molecular Orbital Index Space
The main philosophy of the SSE-MO method is to perform correlated sampling in a joint real-space and occupation-number space (Table 4). Assuming a discretization of 100 points per Cartesian coordinate, the total number of points needed for exhaustive sampling is in the range of 1016 to 1020 as shown in Table 4. However, not all spatial components of all the molecular orbitals contribute equally and uniformly to the calculation of the self-energy. There are certain combinations of MOs whose form in specific regions of the Cartesian space correlate strongly with the error in the self-energy calculations. Through the use of a two-step stratified sampling scheme in both Cartesian and MO space, the SSE-MO method provides a systematic and adaptive procedure to identify the important contributors. We have used a combination of ratio estimator, control-variate, and stratified sampling techniques for the efficient and accurate evaluation of the MO integrals. The key quantity that implements and controls this concept is the Nsamplespace,M,pqst term. This term represents the number of spatial sampling points for the Mth spatial segment for the correction term Dpqrs associated with indices p, q, r, s and depends on both the spatial and MO indices. The total number of sampling points is given by the following expression.
| 123 |
As shown in eq 103, this number was directly obtained from the variance of the integral kernel, which also includes the contribution from the r12–1 operator. Note that these sampling points were not used to evaluate the full r12-integral kernel, but instead were used to evaluate only the component of the full r12-integral kernel not included in the control-variate expression. The Cartesian space sampling for each spatial segment was performed using simple Monte Carlo sampling. This process can be enhanced by using low-discrepancy random numbers, which is a quasi-Monte Carlo approach. We expect that using the quasi-Monte Carlo approach will accelerate the overall calculation process.
Table 4. Total Number of Sampling Points in the Combined MO-Cartesian Space Assuming 100 Points Per Cartesian Coordinate.
| system | N2p1h | N1p2h | NspaceMO | NspaceMO × Nspace |
|---|---|---|---|---|
| Pb4S4 | 3.87 × 104 | 1.76 × 104 | 5.63 × 104 | 5.63 × 1016 |
| Pb44S44 | 5.15 × 107 | 2.34 × 107 | 7.50 × 107 | 7.50 × 1019 |
| Pb140S140 | 1.18 × 109 | 6.37 × 108 | 1.82 × 109 | 1.82 × 1021 |
| Cd6S6 | 7.02 × 105 | 3.32 × 105 | 1.03 × 106 | 1.03 × 1018 |
| Cd24S24 | 4.50 × 107 | 2.13 × 107 | 6.62 × 107 | 6.62 × 1019 |
| Cd45S45 | 2.96 × 108 | 1.40 × 108 | 4.36 × 108 | 4.36 × 1020 |
4.2. Segment-Based Analysis of Sampling Error
The error in the calculated IP using the SSE-MO method originates from the sampling error associated with sampling the integral kernel in the combined Cartesian-MO space. However, not all segments contribute equally to the numerical error. The goal of SSE-MO is to distribute the computational effort in proportion to the contributions from each segment. One insight generated from the SSE-MO calculation is information about the contribution of each segment to the total self-energy operator. We define the cumulative percent contribution for the segments as,
| 124 |
where S(i) is the contribution to the self-energy for each segment. The cumulative percent contribution of the segments to the total self-energy operator is denoted as C(M) and is presented for the PbS and CdS quantum dots in Figures 8 and 9, respectively.
Figure 8.
Cumulative sum of the percent contributions of the segments composing the sample space for the 2p1h and 1p2h terms of the self-energy (ordinate) versus the segment index (abscissa) is displayed. Parts A, B, and C, are for QDs Pb4S4, Pb44S44, and Pb140S140, respectively.
Figure 9.
Cumulative sum of the percent contributions of the segments composing the sample space for the 2p1h and 1p2h terms of the self-energy (ordinate) versus the segment index (abscissa) is displayed. Parts A, B, C are for QDs Cd6S6, Cd24S24, and Cd45S45, respectively.
Analysis of the results revealed that the 2p1h and 1p2h terms show very different behavior. In all cases it was found that only few segments, typically ≤50, had significant contributions to the 1p2h component of the self-energy operator. In contrast, for the 2p1h component, the cumulative sum of the percent contribution increased in a much more gradual manner. The distributions of the standard deviations associated with the segments for the 2p1h and 1p2h terms of the self-energy for the two largest quantum dots, (Pb140S140 and Cd45S45), are presented in Figures 10 and 11, respectively.
Figure 10.
Frequency distributions of the standard deviations (in eV) for the segments that compose the sample space of the 2p1h and 1p2h terms of the self-energy computed for Pb140S140, are displayed.
Figure 11.
Frequency distributions of the standard deviations (in eV) for the segments that compose the sample space of the 2p1h and 1p2h terms of the self-energy computed for Cd45S45, are displayed.
Analysis of the distributions reveals that the sampling error in the 2p1h term is significantly smaller than the sampling error in the 1p2h term for the two largest quantum dots. These plots also show that the overall sampling error in the calculated IP is dominated by the sampling error in the 1p2h term. The advantage of the SSE-MO method is that, by construction, the SSE-MO scheme is able to extract this information dynamically during the course of the calculation and then allocate more sampling points to segments that have high sampling errors. Because SSE-MO is based on stratified sampling, the conventional stratified sampling error analysis69 is applicable for the sampling error in the IP calculations. In addition to this segment-based analysis, the overall sampling error in the calculated IPs as a function of the number of sampling points used to construct the self-energy for Pb140S140 quantum dot is presented in Figure 12.
Figure 12.

Sample standard deviation (σ x̅) in the ionization potential (eV) (ordinate) versus the number of sampling points (abscissa) used to construct the self-energy for the Pb140S140 dot is displayed.
4.3. Connection with Diagrammatic Monte Carlo
The SSE-MO method is conceptually similar to diagrammatic MC (diagMC), where terms are evaluated stochastically. However, there are key differences between the two methods. SSE-MO is not diagram-based and the relative importance of the terms are not evaluated using topological connectivity of the vertices. Also, the SSE-MO method uses stratified sampling as opposed to importance sampling, where emphasis is placed on reducing numerical error through variance minimization and numerical effort is predominantly spent on computing the correction term to the self-energy operator. As an intrinsically adaptive approach, the calculation puts more points where they are needed to achieve reduction of numerical error.
4.3.1. Comparison with Laplace-Transformed Approach
The SSE-MO method does not perform Laplace-transformation, but instead relies on stochastic enumeration to reduce the computational cost. Consequently, only 3D and 6D spatial integrals are solved numerically. As a consequence, higher-order derivatives of the self-energy operator (dnΣ/dωn) can be obtained with relative ease and with very little additional computational cost during the self-energy calculation. This not only allows for calculation of the imaginary component of the self-energy operator, but also open doors for iterative solution of the Dyson equation by Taylor-series expansion of the self-energy operator.
| 125 |
Because we are not using a Laplace transformation, the SSE-MO method is well-suited to extending the self-energy calculation to Σ(3) using the P3 correction developed by Ortiz and co-workers.67 For example, the Laplace transformation of the following term in the P3 expression
 |
126 |
will involve the Monte Carlo numerical integration of a 20-dimensional integral. In the SSE-MO implementation, the dimensionality of the spatial integral will still be six and the MO index will be sampled from the 3p-2h space.
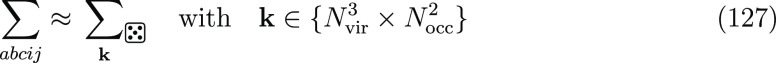 |
127 |
Equation 127 can be viewed as the stochastic tensor contraction over the MO indices and can potentially be applied to other branches of quantum mechanics.
4.4. Selection of Control-Variate Functions
The use of moment-based fitting ensures that the integral of the Mth-order multinomial comes out to be exact. For this work, a maximum of two Gaussian functions were used and was found to be adequate. For more challenging systems, the number of Gaussian functions can be systematically increased. In addition, metrics other than the moments can be used as criteria for the selection of the Gaussian functions. The choice of the control-variate functions is not restricted to Gaussian functions. For QDs, it is possible to take advantage of the approximate spherical symmetry of the system and construct the control-variate functions from the hydrogenic wave functions with effective hole and particle masses.
| 128 |
| 129 |
Although both density fitting70 and the control variate schemes use Gaussian functions, their purpose and implementation are very different. When using the control variate scheme, the goal is to reduce numerical error. When using density fitting, the goal is to approximate it. Specifically in the control variate, the integral of fpq is expressed as
| 130 |
| 131 |
| 132 |
| 133 |
There are two main differences between control variate and density fitting:
-
1.When using the control variate scheme, the error in fitting the integral is always calculated. The error in the estimation of the integral comes from the numerical approximation to the analytical fitting error. If we were to replace the numerical integral, ⟨(f–f0)⟩, by an analytical integral, we would recover the exact integral. The origin of error in density fitting comes from the finite expansion of the auxiliary basis. While in the control variate the error is from the numerical approximation to the residue-error integral, ⟨(f–f0)⟩.

134 -
2.Unlike density-fitting’s attribute of fit-once-use-everywhere, the control variate approach is kernel dependent. This means that the integrals ⟨fpqKA⟩ and ⟨fpqKB⟩ will have different control variate parameters αA and αB, respectively. These parameters are obtained by minimizing the variance as shown below:

135
One approach to do the above integrals efficiently is to first expand the square term and then perform the α-independent integrals separately as shown below.
136 
137 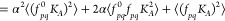
138
5. Conclusions
This work presents the development and implementation of the stratified stochastic enumeration of molecular orbitals (SSE-MO) method for construction of the self-energy operator. The central idea of this method is to express the self-energy operator in a composite space, which is generated by combining the 3D Cartesian space of molecular orbitals with the discrete integer space of the molecular orbital indices. In conjunction, a stratified sampling Monte Carlo scheme was also developed for the efficient evaluation of the complex self-energy operator and its frequency derivatives. The SSE-MO method was applied to a series of CdS and PbS QDs, and the IPs of these QDs were obtained from both single-shot and iterative solution of the second order diagonal approximation to the Dyson equation. The results from these calculations showed that the IPs decreased with increasing dot size. The imaginary component of the self-energy operator was used to construct the single-pole frequency-dependent spectral functions of the quantum dots. The quantum dots with the longest relative lifetimes of the quasi-hole state were identified. The strategy of stochastic enumeration used in the SSE-MO method can also be interpreted in the broader context of stochastic tensor contraction methods and can be applied to other areas of quantum mechanics, where the sequential enumeration of summations is computationally prohibitive.
Acknowledgments
This research was supported by the National Science Foundation under Grant No. CHE-2102437, CHE-1950802, ACI-1341006, and ACI-1541396 and by computational resources provided by Syracuse University.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.2c00329.
Brief description of stratified sampling and common-random-number sampling (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Rudenko A.; Inhester L.; Hanasaki K.; Li X.; Robatjazi S.; Erk B.; Boll R.; Toyota K.; Hao Y.; Vendrell O.; Bomme C.; Savelyev E.; Rudek B.; Foucar L.; Southworth S.; Lehmann C.; Kraessig B.; Marchenko T.; Simon M.; Ueda K.; Ferguson K.; Bucher M.; Gorkhover T.; Carron S.; Alonso-Mori R.; Koglin J.; Correa J.; Williams G.; Boutet S.; Young L.; Bostedt C.; Son S.-K.; Santra R.; Rolles D. Femtosecond response of polyatomic molecules to ultra-intense hard X-rays. Nature 2017, 546, 129–132. 10.1038/nature22373. [DOI] [PubMed] [Google Scholar]
- Jahnke T. Interatomic and intermolecular Coulombic decay: The coming of age story. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 082001. 10.1088/0953-4075/48/8/082001. [DOI] [Google Scholar]
- Averbukh V.; Müller I.; Cederbaum L. Mechanism of interatomic coulombic decay in clusters. Phys. Rev. Lett. 2004, 93, 263002. 10.1103/PhysRevLett.93.263002. [DOI] [PubMed] [Google Scholar]
- McFarland B.; Farrell J.; Miyabe S.; Tarantelli F.; Aguilar A.; Berrah N.; Bostedt C.; Bozek J.; Bucksbaum P.; Castagna J.; Coffee R.; Cryan J.; Fang L.; Feifel R.; Gaffney K.; Glownia J.; Martinez T.; Mucke M.; Murphy B.; Natan A.; Osipov T.; Petrović V.; Schorb S.; Schultz T.; Spector L.; Swiggers M.; Tenney I.; Wang S.; White J.; White W.; Gühr M.. Ultrafast X-ray Auger probing of photoexcited molecular dynamics. Nat. Commun. 2014, 5. 10.1038/ncomms5235 [DOI] [PubMed] [Google Scholar]
- Sansone G.; Pfeifer T.; Simeonidis K.; Kuleff A. Electron correlation in real time. ChemPhysChem 2012, 13, 661–680. 10.1002/cphc.201100528. [DOI] [PubMed] [Google Scholar]
- Jones D.; Yamazaki M.; Watanabe N.; Takahashi M. Electron-impact ionization of the water molecule at large momentum transfer above the double-ionization threshold. Phys. Rev. A 2011, 83, 012704. 10.1103/PhysRevA.83.012704. [DOI] [Google Scholar]
- Aziz E.; Ottosson N.; Faubel M.; Hertel I.; Winter B. Interaction between liquid water and hydroxide revealed by core-hole de-excitation. Nature 2008, 455, 89–91. 10.1038/nature07252. [DOI] [PubMed] [Google Scholar]
- Müller I.; Cederbaum L. Ionization and double ionization of small water clusters. J. Chem. Phys. 2006, 125, 204305. 10.1063/1.2357921. [DOI] [PubMed] [Google Scholar]
- Cederbaum L.; Zobeley J.; Tarantelli F. Giant intermolecular decay and fragmentation of clusters. Phys. Rev. Lett. 1997, 79, 4778–4781. 10.1103/PhysRevLett.79.4778. [DOI] [Google Scholar]
- Ward J. DNA Damage Produced by Ionizing Radiation in Mammalian Cells: Identities, Mechanisms of Formation, and Reparability. Prog. Nucleic Acid Res. Mol. Biol. 1988, 35, 95–125. 10.1016/S0079-6603(08)60611-X. [DOI] [PubMed] [Google Scholar]
- Singh R.; Ortiz J.; Mishra M. Tautomeric forms of adenine: Vertical ionization energies and Dyson orbitals. Int. J. Quantum Chem. 2010, 110 (10), 1901–1915. 10.1002/qua.22363. [DOI] [Google Scholar]
- Chen J.; Schmitz A.; Inerbaev T.; Meng Q.; Kilina S.; Tretiak S.; Kilin D. S. First-Principles Study of p-n-Doped Silicon Quantum Dots: Charge Transfer, Energy Dissipation, and Time-Resolved Emission. J. Phys. Chem. Lett. 2013, 4, 2906–2913. 10.1021/jz400760h. [DOI] [Google Scholar]
- Kilina S. V.; Tamukong P. K.; Kilin D. S. Surface Chemistry of Semiconducting Quantum Dots: Theoretical Perspectives. Acc. Chem. Res. 2016, 49, 2127–2135. 10.1021/acs.accounts.6b00196. [DOI] [PubMed] [Google Scholar]
- Tafen D. N.; Prezhdo O. V. Size and Temperature Dependence of Electron Transfer between CdSe Quantum Dots and a TiO2 Nanobelt. J. Phys. Chem. C 2015, 119, 5639–5647. 10.1021/jp5110278. [DOI] [Google Scholar]
- Zhu H.; Yang Y.; Hyeon-Deuk K.; Califano M.; Song N.; Wang Y.; Zhang W.; Prezhdo O. V.; Lian T. Auger-assisted electron transfer from photoexcited semiconductor quantum dots. Nano Lett. 2014, 14, 1263–1269. 10.1021/nl4041687. [DOI] [PubMed] [Google Scholar]
- Cui P.; Xue Y. Effects of co-adsorption on interfacial charge transfer in a quantum dot dye composite. Nanoscale Res. Lett. 2021, 16 (1), 147. 10.1186/s11671-021-03604-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sardar S.; Kar P.; Remita H.; Liu B.; Lemmens P.; Kumar Pal S.; Ghosh S. Enhanced Charge Separation and FRET at Heterojunctions between Semiconductor Nanoparticles and Conducting Polymer Nanofibers for Efficient Solar Light Harvesting. Sci. Rep. 2015, 5 (1), 17313. 10.1038/srep17313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennehan E. R.; Munson K. T.; Doucette G. S.; Marshall A. R.; Beard M. C.; Asbury J. B. Dynamic Ligand Surface Chemistry of Excited PbS Quantum Dots. J. Phys. Chem. Lett. 2020, 11, 2291–2297. 10.1021/acs.jpclett.0c00539. [DOI] [PubMed] [Google Scholar]
- Padilha L. A.; Robel I.; Lee D. C.; Nagpal P.; Pietryga J. M.; Klimov V. I. Spectral Dependence of Nanocrystal Photoionization Probability: The Role of Hot-Carrier Transfer. ACS Nano 2011, 5, 5045–5055. 10.1021/nn201135k. [DOI] [PubMed] [Google Scholar]
- Dejpasand M. T.; Saievar-Iranizad E.; Bayat A.; Montaghemi A.; Ardekani S. R. Tuning HOMO and LUMO of three region (UV, Vis and IR) photoluminescent nitrogen doped graphene quantum dots for photodegradation of methylene blue. Mater. Res. Bull. 2020, 128, 110886. 10.1016/j.materresbull.2020.110886. [DOI] [Google Scholar]
- Early K. T.; Nesbitt D. Ultrafast Laser Studies of Two-Photon Excited Fluorescence Intermittency in Single CdSe/ZnS Quantum Dots. Nano Lett. 2015, 15, 7781–7787. 10.1021/acs.nanolett.5b01139. [DOI] [PubMed] [Google Scholar]
- Szabo A.; Ostlund N.. Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory; Dover Books on Chemistry; Dover Publications: Mineola, NY, 2012. [Google Scholar]
- Corzo H.; Ortiz J. Electron Propagator Theory: Foundations and Predictions. Adv. Quantum Chem. 2017, 74, 267–298. 10.1016/bs.aiq.2016.05.001. [DOI] [Google Scholar]
- Díaz-Tinoco M.; Dolgounitcheva O.; Zakrzewski V.; Ortiz J. Composite electron propagator methods for calculating ionization energies. J. Chem. Phys. 2016, 144 (22), 224110. 10.1063/1.4953666. [DOI] [PubMed] [Google Scholar]
- Dolgounitcheva O.; Díaz-Tinoco M.; Zakrzewski V.; Richard R.; Marom N.; Sherrill C.; Ortiz J. Accurate Ionization Potentials and Electron Affinities of Acceptor Molecules IV: Electron-Propagator Methods. J. Chem. Theory Comput. 2016, 12, 627–637. 10.1021/acs.jctc.5b00872. [DOI] [PubMed] [Google Scholar]
- Simons J. Equations of motion methods for computing electron affinities and ionization potentials. Encycl. Comput. Chem. 2005, 443–464. 10.1002/0470845015.cn0065. [DOI] [Google Scholar]
- Herman M.; Freed K.; Yeager D.; Liu B. Critical test of equation-of-motion-Green’s function methods. II. Comparison with configuration interaction results. J. Chem. Phys. 1980, 72, 611–620. 10.1063/1.438951. [DOI] [Google Scholar]
- Herman M.; Yeager D.; Freed K. Analysis of third order contributions to equations of motion-green’s function ionization potentials: Application to N2. Chem. Phys. 1978, 29, 77–96. 10.1016/0301-0104(78)85063-0. [DOI] [Google Scholar]
- Freed K.; Yeager D. A wavefunction approach to equations of motion-Green’s function methods. Chem. Phys. 1977, 22, 401–414. 10.1016/0301-0104(77)89027-7. [DOI] [Google Scholar]
- Chen T.-T.; Simons J.; Jordan K. Analysis of the equation-of-motion theory of electron affinities and ionization potentials. Chem. Phys. 1976, 14, 145–158. 10.1016/0301-0104(76)80033-X. [DOI] [Google Scholar]
- Simons J.; Smith W. Theory of electron affinities of small molecules. J. Chem. Phys. 1973, 4908–4911. [Google Scholar]
- Schirmer J.; Cederbaum L.; Walter O. New approach to the one-particle Green’s function for finite Fermi systems. Phys. Rev. A 1983, 28, 1237–1259. 10.1103/PhysRevA.28.1237. [DOI] [Google Scholar]
- Cederbaum L. Direct calculation of ionization potentials of closed-shell atoms and molecules. Theoret. Chim. Acta 1973, 31, 239–260. 10.1007/BF00526514. [DOI] [Google Scholar]
- Nooijen M.; Snijders J. Coupled cluster Green’s function method: Working equations and applications. Int. J. Quantum Chem. 1993, 48, 15–48. 10.1002/qua.560480103. [DOI] [Google Scholar]
- Nooijen M.; Snijders J. Coupled cluster approach to the single-particle Green’s function. Int. J. Quantum Chem. 1992, 44, 55–83. 10.1002/qua.560440808. [DOI] [Google Scholar]
- Ranasinghe D.; Margraf J.; Perera A.; Bartlett R. Vertical valence ionization potential benchmarks from equation-of-motion coupled cluster theory and QTP functionals. J. Chem. Phys. 2019, 150, 074108. 10.1063/1.5084728. [DOI] [PubMed] [Google Scholar]
- Kamiya M.; Hirata S. Higher-order equation-of-motion coupled-cluster methods for ionization processes. J. Chem. Phys. 2006, 125, 074111. 10.1063/1.2244570. [DOI] [PubMed] [Google Scholar]
- Hirata S.; Nooijen M.; Bartlett R. High-order determinantal equation-of-motion coupled-cluster calculations for electronic excited states. Chem. Phys. Lett. 2000, 326, 255–262. 10.1016/S0009-2614(00)00772-7. [DOI] [Google Scholar]
- Pieniazek P.; Arnstein S.; Bradforth S.; Krylov A.; Sherrill C. Benchmark full configuration interaction and equation-of-motion coupled-cluster model with single and double substitutions for ionized systems results for prototypical charge transfer systems: Noncovalent ionized dimers. J. Chem. Phys. 2007, 127, 164110. 10.1063/1.2795709. [DOI] [PubMed] [Google Scholar]
- Opalka D.; Pham T. A.; Sprik M.; Galli G. The ionization potential of aqueous hydroxide computed using many-body perturbation theory. J. Chem. Phys. 2014, 141, 034501. 10.1063/1.4887259. [DOI] [PubMed] [Google Scholar]
- Hirata S.; Hermes M. R.; Simons J.; Ortiz J. V. General-order many-body green’s function method. J. Chem. Theory Comput. 2015, 11, 1595–1606. 10.1021/acs.jctc.5b00005. [DOI] [PubMed] [Google Scholar]
- Govoni M.; Galli G. Large Scale GW Calculations. J. Chem. Theory Comput. 2015, 11, 2680–2696. 10.1021/ct500958p. [DOI] [PubMed] [Google Scholar]
- Bartlett R. J. Towards an exact correlated orbital theory for electrons. Chem. Phys. Lett. 2009, 484, 1–9. 10.1016/j.cplett.2009.10.053. [DOI] [Google Scholar]
- Maitra N. Perspective: Fundamental aspects of time-dependent density functional theory. J. Chem. Phys. 2016, 144, 220901. 10.1063/1.4953039. [DOI] [PubMed] [Google Scholar]
- Casida M.; Huix-Rotllant M. Progress in time-dependent density-functional theory. Annu. Rev. Phys. Chem. 2012, 63, 287–323. 10.1146/annurev-physchem-032511-143803. [DOI] [PubMed] [Google Scholar]
- Runge E.; Gross E. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 1984, 52, 997–1000. 10.1103/PhysRevLett.52.997. [DOI] [Google Scholar]
- Elkind P. D.; Staroverov V. N. Energy expressions for Kohn-sham potentials and their relation to the Slater-janak theorem. J. Chem. Phys. 2012, 136, 124115. 10.1063/1.3695372. [DOI] [PubMed] [Google Scholar]
- Knight J.; Wang X.; Gallandi L.; Dolgounitcheva O.; Ren X.; Ortiz J.; Rinke P.; Körzdörfer T.; Marom N. Accurate Ionization Potentials and Electron Affinities of Acceptor Molecules III: A Benchmark of GW Methods. J. Chem. Theory Comput. 2016, 12, 615–626. 10.1021/acs.jctc.5b00871. [DOI] [PubMed] [Google Scholar]
- Ortiz J. Electron propagator theory: An approach to prediction and interpretation in quantum chemistry. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2013, 3, 123–142. 10.1002/wcms.1116. [DOI] [Google Scholar]
- Pokhilko P.; Izmodenov D.; Krylov A. I. Extension of frozen natural orbital approximation to open-shell references: Theory, implementation, and application to single-molecule magnets. J. Che. Phys. 2020, 152, 034105. 10.1063/1.5138643. [DOI] [PubMed] [Google Scholar]
- Vlcek V.; Rabani E.; Neuhauser D.; Baer R. Stochastic GW calculations for molecules. J. Chem. Theory Comput. 2017, 13, 4997–5003. 10.1021/acs.jctc.7b00770. [DOI] [PubMed] [Google Scholar]
- Willow S. Y.; Kim K. S.; Hirata S. Stochastic evaluation of second-order Dyson self-energies. J. Chem. Phys. 2013, 138, 164111. 10.1063/1.4801862. [DOI] [PubMed] [Google Scholar]
- Doran A. E.; Hirata S. Stochastic evaluation of fourth-order many-body perturbation energies. J. Chem. Phys. 2021, 154, 134114. 10.1063/5.0047798. [DOI] [PubMed] [Google Scholar]
- Lestrange P. J.; Peng B.; Ding F.; Trucks G. W.; Frisch M. J.; Li X. Density of States Guided Møller-Plesset Perturbation Theory. J. Chem. Theory Comput. 2014, 10, 1910–1914. 10.1021/ct400765a. [DOI] [PubMed] [Google Scholar]
- Rubinstein R. Stochastic enumeration method for counting NP-Hard problems. Methodol. Comput. Appl. Probab. 2013, 15, 249–291. 10.1007/s11009-011-9242-y. [DOI] [Google Scholar]
- Press W. H.; Teukolsky S. A.; Vetterling W. T.; Flannery B. P.. Numerical recipes in Fortran 90 the art of parallel scientific computing; Cambridge University Press: Cambridge, U.K., 1996. [Google Scholar]
- Lemieux C.Monte Carlo and Quasi-Monte Carlo Sampling; Springer Series in Statistics; Springer: New York, 2009. [Google Scholar]
- Leobacher G.; Pillichshammer F.. Introduction to Quasi-Monte Carlo Integration and Applications; Compact Textbooks in Mathematics; Springer International Publishing: New York, 2014. [Google Scholar]
- Fetter A.; Walecka J.. Quantum Theory of Many-particle Systems; Dover Books on Physics; Dover Publications: Mineola, NY, 2003. [Google Scholar]
- Díaz-Tinoco M.; Dolgounitcheva O.; Zakrzewski V.; Ortiz J. Composite electron propagator methods for calculating ionization energies. J. Chem. Phys. 2016, 144, 224110. 10.1063/1.4953666. [DOI] [PubMed] [Google Scholar]
- Nooijen M.; Snijders J. G. Coupled cluster approach to the single-particle Green’s function. Int. J. Quantum Chem. 1992, 44, 55–83. 10.1002/qua.560440808. [DOI] [Google Scholar]
- Casida M. E.; Chong D. P. Quasi-particle equation from the configuration-interaction (CI) wave-function method. Int. J. Quantum Chem. 1991, 40, 225–242. 10.1002/qua.560400206. [DOI] [Google Scholar]
- Ping Y.; Rocca D.; Galli G. Electronic excitations in light absorbers for photoelectrochemical energy conversion: First principles calculations based on many body perturbation theory. Chem. Soc. Rev. 2013, 42, 2437–2469. 10.1039/c3cs00007a. [DOI] [PubMed] [Google Scholar]
- Kronik L.; Makmal A.; Tiago M. L.; Alemany M. M. G.; Jain M.; Huang X.; Saad Y.; Chelikowsky J. R. PARSEC – the pseudopotential algorithm for real-space electronic structure calculations: recent advances and novel applications to nano-structures. Phys. Status Solidi B 2006, 243, 1063–1079. 10.1002/pssb.200541463. [DOI] [Google Scholar]
- Description of stratified sampling and common random number sampling is presented in the SI.
- Willow S. Y.; Kim K. S.; Hirata S. Stochastic evaluation of second-order Dyson self-energies. J. Chem. Phys. 2013, 138, 164111. 10.1063/1.4801862. [DOI] [PubMed] [Google Scholar]
- Ortiz J. A nondiagonal, renormalized extension of partial third-order quasiparticle theory: Comparisons for closed-shell ionization energies. J. Chem. Phys. 1998, 108, 1008–1014. 10.1063/1.475463. [DOI] [Google Scholar]
- Johnson R. D.NIST Computational Chemistry Comparison and Benchmark Database. http://cccbdb.nist.gov/ (Accessed May 20, 2022).
- Shields M. D.; Teferra K.; Hapij A.; Daddazio R. P. Refined stratified sampling for efficient Monte Carlo based uncertainty quantification. Reliab. Eng. Syst. Saf. 2015, 142, 310–325. 10.1016/j.ress.2015.05.023. [DOI] [Google Scholar]
- Jung Y.; Sodt A.; Gill P. M.; Head-Gordon M. Auxiliary basis expansions for large-scale electronic structure calculations. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 6692–6697. 10.1073/pnas.0408475102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.










