Log-transformation of independent variables: must we?

Abstract

Epidemiologic studies often quantify exposure using biomarkers, which commonly have statistically skewed distributions. Although normality assumption is not required if the biomarker is used as an independent variable in linear regression, it has become common practice to log-transform the biomarker concentrations. This transformation can be motivated by concerns for non-linear dose–response relationship or outliers, however, such transformation may not always reduce bias. In this study, we evaluated the validity of motivations underlying the decision to log-transform an independent variable using simulations, considering eight scenarios that can give rise to skewed X and normal Y. Our simulation study demonstrates that (1) if the skewness of exposure did not arise from a biasing factor (e.g., measurement error), the analytic approach with the best overall model fit best reflected the underlying outcome generating methods and was least biased, regardless of the skewness of X and (2) all estimates were biased if the skewness of exposure was a consequence of a biasing factor. We additionally illustrate a process to determine whether the transformation of an independent variable is needed using NHANES. Our study and suggestion to divorce the shape of the exposure distribution from the decision to log-transform it may aid researchers in planning for analysis using biomarkers or other skewed independent variables.

INTRODUCTION

Epidemiologic research often quantifies human exposures in terms of concentrations measured in a biospecimen such as urine, blood, or tissue (i.e., biomarkers of exposure). Whether they are compounds of interest or metabolic byproducts, biomarkers often have defining characteristics: positive values, low concentrations with few extremely high observations, oftentimes resulting in non-normal, statistically “skewed” distributions. It is commonly observed that biomarkers of environmental exposures, such as phthalate metabolites and heavy metals measured in urine, are highly skewed to the right (1), as are biomarkers of micronutrients (e.g., vitamin D (2), triglycerides (3)) and clinical endpoints (e.g., c-reactive protein (4), hemoglobin A1C (5)).

When evaluating the relation between a skewed exposure and a health endpoint using regression, it has become common practice to use the log value of the exposure (hereafter “log-transform”) as the independent variable in regression models rather than the original measured values (6). Transformations of independent variables to improve model fit have a long history (7) and log-transformation has become a de facto standard. Motivations for log-transforming independent variables stated in the literature include addressing nonlinear or nonadditive dose–response relationship (8, 9), reducing outlier influence (10, 11), reporting study results in a format that is directly comparable with previous publications, or responding to the misconception that independent variables must conform to specific distributional assumptions (e.g., normality). Because log-transformation of independent variables fundamentally alters the interpretation of regression coefficients, careful selection of exposure transformations is warranted. One parsimonious approach to approximating the true, non-linear dose–response relationship in regression models is by iteratively power-transforming exposure, including log-transformation, and selecting the transformation method that best normalizes the error term, as described by Box and Tidwell (7, 12). However, such assessments are rarely described in the literature and motivations for log-transformations are often left unstated, leaving open the possibility that log-transformation of exposure is done out of habit rather than principle.

In this paper, we review motivations underlying log-transformation of skewed independent variables given in the literature and use simulations to illustrate the need to divorce the shape of the exposure distribution from the decision to log-transform it. Finally, we demonstrate a process for deciding between log-transforming an independent variable or leaving it untransformed, using a case study of blood lead and blood pressure in National Health and Nutrition Examination Survey (NHANES). NHANES data were deidentified and therefore IRB review of this study was not required

DESCRIPTION OF THE PROBLEM

The scenario addressed in this manuscript arises when the goal is to learn about associations between some continuous exposure (X) and an outcome (Y) using regression methods. Often, such models will be in the form of a generalized linear model $g\left(E\left(Y|\mathit{X},\mathit{\beta }\right)\right)={\beta }_0+h\left(\mathit{X}\right){\mathit{\beta }}_x$, where g(⋅) is the link function and h(X) is some transformation of the exposure (e.g., no transformation, spline basis function, log-transformation) and β_x is the set of parameters of interest. Such models typically include distributional assumptions, such as in linear regression where $Y-E\left(Y|\mathit{X},\mathit{\beta }\right)$ is assumed to follow a normal (Gaussian) distribution, such that Y is “conditionally normal.” An often informally given motivation for log-transforming exposure is to approximate a normal distribution for the transformed exposure. For an exposure that follows log–normal distribution, log-transformation results in a normally distributed variable; however, log-transformation can introduce more skewness or spread if exposure follows other distributions (13, 14). Even when log-transformation results in a normal distribution, such distributional assumptions are required for the error term, not for independent variables (12). While log-transformation of exposure may be useful for exploring exposure distributions or estimating quantities such as geometric means, normality of exposures is not a prerequisite for estimating their relationship with on a health outcome in regression models. Aside from this mistaken reasoning, two other commonly cited and testable motivations for log-transforming independent variables are to conform to non-linear dose–response (8, 9) or reduce any potential impacts of outliers (10, 11).

SIMULATION EXAMPLE

We consider a study in which we are interested in assessing the relation between a skewed independent variable (X) and a conditionally normal dependent variable (Y) via a linear regression model. In this setting, we use simulated data to explore the validity of motivations for log-transformation of independent variables. The fact that an independent variable does not follow a normal distribution oftentimes motivates its log-transformation. Therefore, we explore several settings that can give rise to skewed exposure distribution, including 1) truly log–normal distribution, and distributions that appear skewed due to other factors: 2) truncation, 3) mixed distribution, and 4) measurement error.

Data generation methods

We consider a total of eight scenarios, with four X generation methods (XGs) motivated by the above scenarios and two Y generation methods (YGs) representing different exposure-response scenarios (Table 1). Y is generated with either $E\left(Y\right|X)=0.3*X$ [YG_Add] or $E\left(Y|X\right)=0.3*ln\left(X\right)$ [YG_Mult], which addresses the motivation to transform exposure to meet theoretical dose–response functions. For each YG, we consider four different XGs including three that may give rise to skewness and/or outliers without X following a log–normal distribution.

1. XG_LogN: We start with a simple case where X is drawn from a log–normal distribution (XG_LogN; $ln\left(X\right)~N(\mu ,\sigma ))$.

2. XG_TrncN: We use a simple alternative to log–normal distribution by drawing X from a normal distribution that is truncated at 0.01 (XG_TrncN; $X~TN(a=0.01,\mu ,3\sigma ))$.

3. XG_Mixed: We address the situation when a skewed distribution arises because a study sample consists of two or more subpopulations, in what is sometimes known as a “mixture” distribution (15). For example, individuals who encounter chemicals in workplaces or reside in contaminated areas can experience exposures that are substantially higher than that occurring in typical, daily exposures in the general population. We operationalize the mixture distribution (XG_Mixed) by drawing X from a normal distribution truncated at 0.01 ($X~TN(a=0.01,\mu ,3\sigma ))$ with probability 0.8 and another truncated normal distribution ($X~TN(a=0.01,1.5\mu ,9\sigma )$) with probability 0.2, implying a mixture of two truncated-normal distributions.

4. XG_MErr: Last, we considered an outlier generation method through measurement error (XG_MErr). XG_MErr was generated in three steps: 1) generate X from normal distribution truncated at 0.01 ($X~TN(a=0,\mu ,3\sigma )$), 2) generate Y using X, according to YGs, and 3) randomly select 5% of X to introduce random noise that is proportional to the original values of X. As a result, X in XG_MErr consists of 95% of X with perfect measurement and 5% of X with measurement error that can result in outliers (i.e., data points with values of Y that do not follow the trend of rest of the data) and/or high leverage observations (i.e., extremely high or low values of X).

Table 1.

Data generation methods of X and Y used in the simulation studies.

Notation	Description	Parameters
X generation methods (XGs)
XGLogN	X follows log-normal distribution	ln(X) ∼ N(μ = 0.42, σ = 0.8)
XGTrncN	X follows normal distribution, truncated at zero	X ∼ TN (a = 0.01, μ = 0.42, σ = 2.4)
XGMixed	X follows skewed distribution due to mixed distribution (two truncated normal)	80% of X ∼ TN (a = 0.01, μ = 0.42, σ = 2.4) 20% of X ∼ TN (a = 0.01, μ = 0.63, σ = 7.2)
XGMErr	X follows skewed distribution due to measurement error	95% of X ∼ XTrutha 5% of X ∼ XTrutha*MErrb
Y generation methods (YGs)
YGAdd	Additive associations between X and Y	Y = βXc*X + Errord
YGMult	Multiplicative associations between X and Y	Y = βXc*ln(X) + Errord

Abbreviations: ln, natural log; μ, mean; σ, standard deviation; a, lower truncation point; N, normal distribution; TN, truncated normal distribution.

^aX_Truth: true values of X measured without error, which follows TN(a = 0.01, μ = 0.42, σ = 2.4)

^bMErr: measurement error that is proportional to the true values of X, which follows TN(a=0.01, μ = 1, σ =2).

^cβ_X: linear regression coefficient of the untransformed/transformed X, which was set to 0.3.

^dError: linear regression error term, which follows ∼ N(0,1)

We note here that, for XG_LogN, XG_TrncN, and XG_Mixed, one could expect to find an estimator of the dose–response relationship that achieves no bias. XG_MErr represents a more realistic case where the best that one could hope for (absent a formal correction for measurement error bias), is to find an estimator with the lowest bias in a given setting.

We demonstrate the impact of log-transforming an independent variable on estimation and model fit using simple simulations. Using the XGs and YGs described previously, we performed 1000 simulations for a hypothetical study assessing the impact of skewed X with a continuous Y that follows normal distribution, in a sample size of 500. For the sake of simplicity, we assume no confounding or selection bias. As sensitivity analyses, we considered alternative distributions of X, strengths of association, and sample size.

Data analysis methods

For each combination of XG and YG, we estimate an association between X and Y using a linear regression model (LM) with X or ln(X). Since concerns for outliers may motivate the log-transformation of X, we consider an alternative regression analysis using robust linear models. The robust linear model uses M-estimation, which, like least squares, minimizes a function of the residuals; unlike least squares, however, it penalizes large residuals less severely, which reduces outlier impact in expectation (16). For each regression model, we summarize the overall model performance across the 1,000 simulated datasets using average log–likelihood. We note here that bias of regression coefficients is not a meaningful comparison of two approaches because regression with two different transformations of exposure implies fundamentally distinct regression curves, except under the null. Hence, we focus on assessing bias via averaging predicted values of Y at specific percentiles of X, denoted $\stackrel{-}{p}(y|x_q)$ where x_q is the theoretical qth percentile of X and $\stackrel{-}{p}$ is the mean of predicted values. For X percentiles 25^th, 50^th, and 75^th, we generated the following parameters: we generated the following parameters: mean bias (parameter estimate minus truth averaged across all simulations), mean percent bias (bias over truth multiplied by 100 averaged across all simulations), and mean 95% confidence interval coverage (proportion of 95% confidence interval including the truth averaged across all simulations). Asymptotically derived 95% confidence intervals (estimate ± 1.96*standard error derived from the model covariance matrix) were used in the simulation to estimate 95% confidence interval coverage, since Ys were not transformed and there was no covariate adjustment.

We also estimated marginal effects of changing all X from its 75^th to 50^th theoretical percentiles (and 50^th to 25^th theoretical percentiles). Two exposure contrasts (i.e., 75^th to 50^th and 50^th to 25^th theoretical percentiles) could also be conceived as two distinct, absolute change in exposure levels (e.g., 0.78 ug/dL and 0.47 ug/dL decrease in blood lead). In the current simulation section, we report the exposure contrast using percentiles because the units are arbitrary in our simulation; in the real-world example section using NHANES, we include the values equivalent to the exposure contrast values. Further, additive relations between Y and log(X) would imply multiplicative relations in another scale (e.g., Y and X) that results in an effect estimate per 1 unit increase in X that changes depending on the value of X, rather than being constant. The average absolute difference in predicted values of Y with a quartile increase in X was defined as $\stackrel{-}{p}(y|x_{q_1})-\stackrel{-}{p}(y|x_{q0})$ where x_q1 and x_q0 are the theoretical X percentiles. We generated mean bias, mean percent bias, mean root mean squared error (i.e., standard deviation of predicted value minus truth, averaged across all simulations), and Monte Carlo standard deviation (i.e., standard deviation of beta coefficients across 1,000 simulated datasets).

We conducted all analyses with R version 4.1 and robust linear regression using package ‘MASS’ with MM estimator, which is an M-estimator with Tukey’s biweight and fixed scale (16).

Results

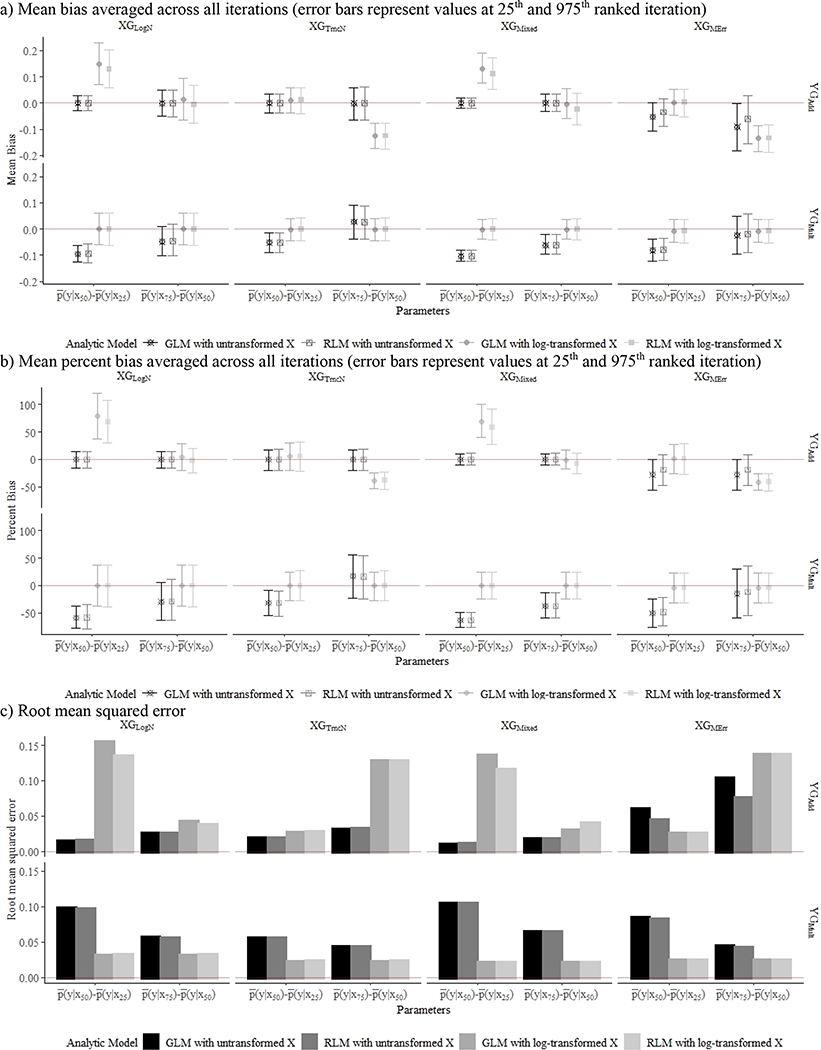
Simulation results are summarized in terms of overall model fit (Table 2), parameter estimates for expected values of Y at X percentiles (Table 2), and bias in expected differences in Y per a quartile increase in X (Figure 1). In the absence of measurement error (i.e., all data generation methods for X except XG_MErr), the analytic approach that best reflected the data generation methods of Y resulted in the least biased estimates and best model fit across all data generation methods. For example, expected values of Y modeled with generalized linear models or robust linear models with untransformed X were least biased with coverage close to 95%, when the true dose–response relationship was linear (YG_Add), even in the presence of outliers (XG_Mixed). Using log-transformed X when the true dose–response is linear resulted in biased estimates, with greater average bias at lower X percentiles across all data generation methods except for XG_LogN (Table 2). Incorrect model specification (e.g., log-transformed X for YG_Add) yielded biased effect estimates, with the extent of bias varying by the exposure contrast, for both generalized and robust linear models (Figure 1).

Table 2.

Average predicted values of Y at X percentiles for each combination of X generation method (XG) and Y data generation method (YG), estimated with four linear regression models (n=500; iteration=1000)

XG	Analytic model	X percentile	YG
			YGAdd				YGMult
			E(Y)	Mean %bias	Coverage	Average ll	E(Y)	Mean %bias	Coverage	Average ll
XG LogN	GLM with untransformed X	25th	0.27	−0.24	0.95	−708	−0.04	−97.63	0.89	−712
		50th	0.46	−0.23	0.94	−708	0.13	−48.16	0.73	−712
		75th	0.78	−0.22	0.93	−708	0.29	−37.88	0.36	−712
	RLM with untransformed X	25th	0.27	−0.10	0.94	−708	−0.04	−95.50	0.88	−712
		50th	0.46	−0.12	0.93	−708	0.13	−48.03	0.72	−712
		75th	0.78	−0.13	0.93	−708	0.29	−37.27	0.38	−712
	GLM with ln(X)	25th	0.27	8.07	0.92	−732	−0.04	2.97	0.95	−708
		50th	0.46	37.34	0.05	−732	0.13	−1.11	0.94	−708
		75th	0.78	23.41	0.13	−732	0.29	−0.60	0.94	−708
	RLM with ln(X)	25th	0.27	11.62	0.89	−732	−0.04	1.73	0.95	−708
		50th	0.46	35.11	0.08	−732	0.13	−0.64	0.93	−708
		75th	0.78	19.59	0.25	−732	0.29	−0.34	0.93	−708
XG TrncN	GLM with untransformed X	25th	0.27	0.19	0.95	−709	−0.04	180.48	0.80	−715
		50th	0.46	0.03	0.94	−709	0.13	−92.30	0.33	−715
		75th	0.78	−0.06	0.94	−709	0.29	−30.89	0.53	−715
	RLM with untransformed X	25th	0.27	0.37	0.94	−709	−0.04	174.25	0.80	−715
		50th	0.46	0.14	0.93	−709	0.13	−90.83	0.34	−715
		75th	0.78	0.00	0.93	−709	0.29	−30.48	0.53	−715
	GLM with ln(X)	25th	0.27	67.82	0.06	−723	−0.04	−2.23	0.94	−709
		50th	0.46	41.79	0.02	−723	0.13	−0.24	0.94	−709
		75th	0.78	8.28	0.76	−723	0.29	−0.49	0.94	−709
	RLM with ln(X)	25th	0.27	66.90	0.08	−723	−0.04	−3.54	0.94	−709
		50th	0.46	41.37	0.03	−723	0.13	0.13	0.93	−709
		75th	0.78	8.10	0.75	−723	0.29	−0.33	0.94	−709
XG Mixed	GLM with untransformed X	25th	0.27	0.08	0.93	−708	−0.04	−62.78	0.92	−719
		50th	0.46	0.02	0.93	−708	0.13	−63.97	0.64	−719
		75th	0.78	−0.01	0.94	−708	0.29	−49.23	0.14	−719
	RLM with untransformed X	25th	0.27	0.23	0.93	−709	−0.04	−69.30	0.91	−719
		50th	0.46	0.12	0.92	−709	0.13	−62.15	0.66	−719
		75th	0.78	0.05	0.93	−709	0.29	−48.45	0.15	−719
	GLM with ln(X)	25th	0.27	68.84	0.15	−772	−0.04	−3.04	0.94	−709
		50th	0.46	68.98	0	−772	0.13	0.09	0.94	−709
		75th	0.78	39.65	0	−772	0.29	−0.30	0.94	−709
	RLM with ln(X)	25th	0.27	66.25	0.17	−773	−0.04	−4.34	0.93	−709
		50th	0.46	62.94	0	−773	0.13	0.46	0.93	−709
		75th	0.78	33.48	0	−773	0.29	−0.14	0.94	−709
XG MErr	GLM with untransformed X	25th	0.27	30.28	0.67	−720	−0.04	49.34	0.90	−718
		50th	0.46	6.07	0.89	−720	0.13	−79.00	0.47	−718
		75th	0.78	−8.05	0.71	−720	0.29	−43.12	0.27	−718
	RLM with untransformed X	25th	0.27	19.38	0.79	−722	−0.04	59.58	0.89	−719
		50th	0.46	3.54	0.92	−722	0.13	−79.33	0.46	−719
		75th	0.78	−5.70	0.80	−722	0.29	−41.33	0.30	−719
	GLM with ln(X)	25th	0.27	69.27	0.06	−724	−0.04	−11.66	0.93	−709
		50th	0.46	40.71	0.03	−724	0.13	−3.04	0.94	−709
		75th	0.78	6.53	0.83	−724	0.29	−4.11	0.94	−709
	RLM with ln(X)	25th	0.27	68.27	0.07	−724	−0.04	−11.67	0.93	−709
		50th	0.46	40.27	0.03	−724	0.13	−2.84	0.94	−709
		75th	0.78	6.36	0.83	−724	0.29	−3.94	0.94	−709

Abbreviations: Coverage, 95% confidence interval coverage; ll, log-likelihood.

^aXG_LogN: ln(X) ∼ N(μ=0.42, σ=0.8)

^bXG_TruncN: X ∼ TN (a=0.01, μ=0.42, σ=2.4)

^cXG_Mixed: 80% of X ∼ TN (a=0.01, μ=0.42, σ=2.4), 20% of X ∼ TN (a=0.01, μ=0.63, σ=7.2)

^dXG_MErr; 95% of X ∼ X_Truth, 5% of X ∼ X_Truth*MErr, where X_Truth ∼TN(a=0.01, μ=0.42, σ=2.4) and MErr ∼ TN(a=0.01, μ=1, σ=2).

^eYG_Add; Y = 0.3X + N(0,1).

^fYG_Mult: Y = 0.3ln(X) + N(0,1).

Figure 1.

Mean bias (a), percent bias (b), and root mean squared error (c) associated with $\stackrel{-}{p}\left(y|x_{q1}\right)-\stackrel{-}{p}\left(y|x_{q0}\right)$. Each figure contains results from 8 X generation method (XGs) and Y data generation methods (YGs) across 1000 simulations with a sample size of 500, with additive YG presented in the top row and multiplicative YG in the bottom row.

^aXG_LogN: ln(X) ~ N(μ=0.42, σ=0.8); ^bXG_TruncN: X ~ TN (a=0.01, μ=0.42, σ=2.4); ^cXG_Mixed: 80% of X ~ TN (a=0.01, μ=0.42, σ=2.4), 20% of X ~ TN (a=0.01, μ=0.63, σ=7.2); ^dXG_MErr; 95% of X ~ X_Truth, 5% of X ~ X_Truth*MErr, where X_Truth ~TN(a=0.01, μ=0.42, σ=2.4) and MErr ~ TN(a=0.01, μ=1, σ=2).; ^eYG_Add; Y = 0.3X + N(0,1).; ^fYG_Mult: Y = 0.3ln(X) + N(0,1).

In XG_MErr, whereby outliers were introduced from measurement error, all models yielded biased estimates. Mean bias of expected Y values were over 5% for all analytic models. When the true dose–response relationship was linear (YG_Add), expected Ys were more biased at Q1 and Q3 than at Q2; incorrect model specification resulted in the most biased estimates when the true dose–response was on a multiplicative scale (YG_Mult).

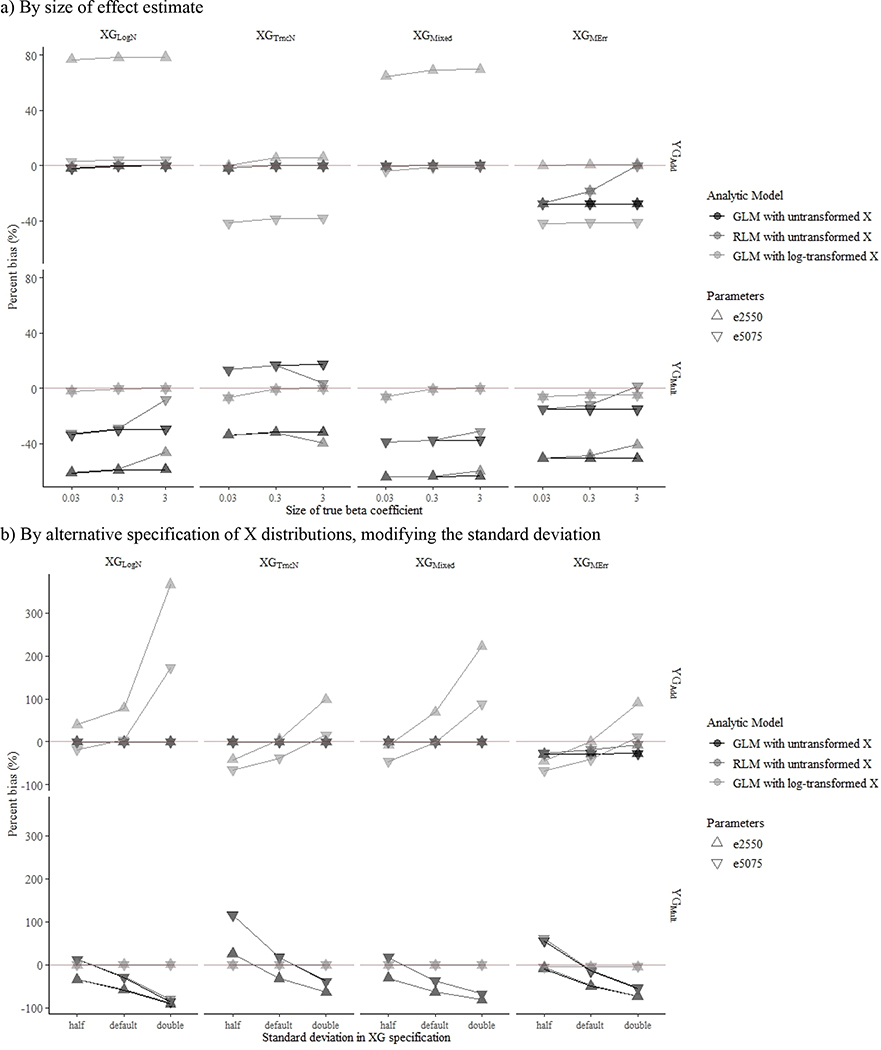
In the case of YG_Mult with incorrect model specification (i.e., untransformed X), robust linear models generally yielded less biased effect estimates than that from generalized linear models when true effect sizes were larger (Figure 2a). We also observed that incorrect model specification yielded greater bias in more skewed X distributions (Figure 2b). When we repeated the simulation with smaller sample size, results were similar to those of the primary analyses.

Figure 2.

Impact of effect size and skewness on the estimation of mean percent bias associated with average absolute difference in predicted Y per exposure contrast ($△:\stackrel{-}{p}\left(y|x_{50}\right)-\stackrel{-}{p}\left(y|x_{25}\right)$▽: $\stackrel{-}{p}\left(y|x_{75}\right)-\stackrel{-}{p}\left(y|x_{50}\right)$). Each figure contains results from 8 X generation method (XGs) and Y data generation methods (YGs) across 1000 simulations with a sample size of 500, with additive YG presented in the top row and multiplicative YG in the bottom row.

^aXG_LogN: ln(X) ~ N(μ=0.42, σ=0.8); ^bXG_TruncN: X ~ TN (a=0.01, μ=0.42, σ=2.4); ^cXG_Mixed: 80% of X ~ TN (a=0.01, μ=0.42, σ=2.4), 20% of X ~ TN (a=0.01, μ=0.63, σ=7.2); ^dXG_MErr; 95% of X ~ X_Truth, 5% of X ~ X_Truth*MErr, where X_Truth ~TN(a=0.01, μ=0.42, σ=2.4) and MErr ~ TN(a=0.01, μ=1, σ=2).; ^eYG_Add; Y = 0.3X + N(0,1).; ^fYG_Mult: Y = 0.3ln(X) + N(0,1).

APPLIED EXAMPLE: BLOOD LEAD AND BLOOD PRESSURE

To illustrate the process of dealing with skewed independent variables, we present as an example an investigation of a well-studied relationship between blood lead and blood pressure using NHANES 1999–2016. Although several studies have examined links between blood lead and blood pressure in NHANES (17–22), results are reported with blood lead in a mixed format: log-transformed, untransformed continuous, or categorical.

In this example, we evaluate exposure response functions between blood lead concentrations and systolic blood pressure. Similar to previous literature, we restricted NHANES participants to non-pregnant adults (20–79 years) who were not on anti-hypertensive medication and had complete data on blood lead concentrations (ug/dL), blood pressure (mmHg) measurements, and commonly adjusted covariates: age, education, race/ethnicity, household income, hypertension medication status, and waist circumference. We calculated systolic blood pressure (mmHg) following Centers for Disease Control and Prevention (CDC) recommendations, to average across blood pressure readings excluding the first reading unless only one is provided, in which case the one reading serves as the average (23). Since our outcome variable, systolic blood pressure, was right-skewed, we applied Box–Cox transformation. We transformed systolic blood pressure with a lambda of −1.23, where lambda was selected by methods described by Box and Tidwell (7).

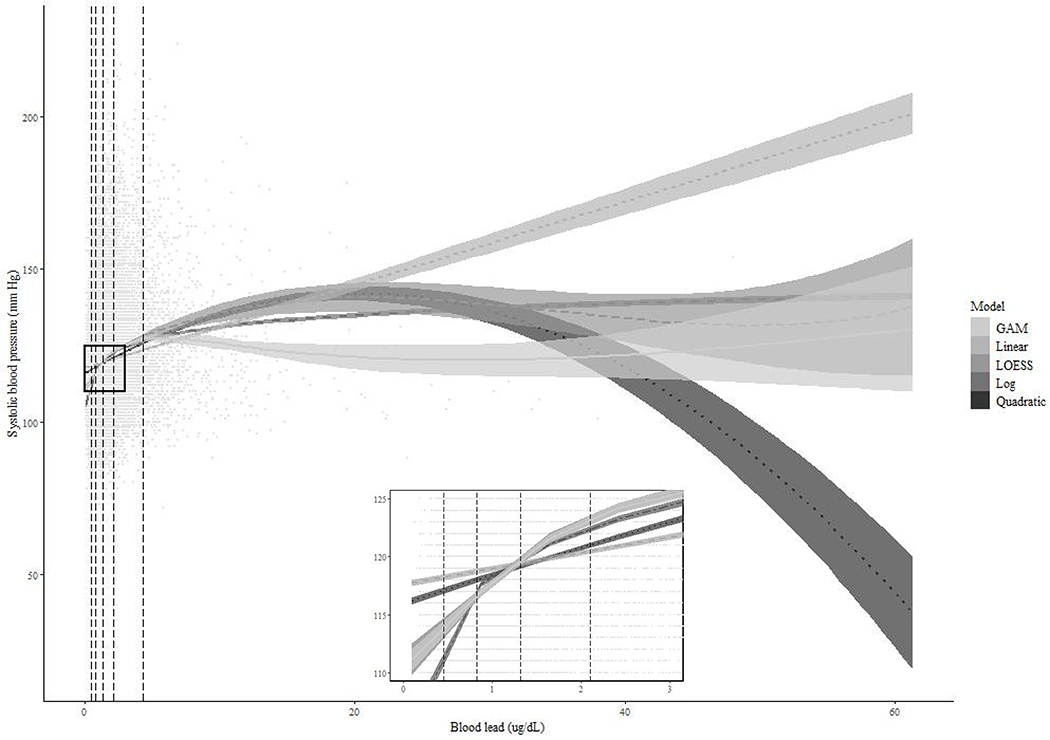
The study sample consisted of 23,113 individuals whose median blood pressure and lead were 118 mmHg (IQR: 109–128 mmHg) and 1.32 ug/dL (0.83–2.10 ug/dL), respectively. Distributions of blood lead concentrations were lower among females (median: 1.09 ug/dL; IQR: 0.70–1.68 ug/dL) than males (1.61 ug/dL; 1.03–2.55 ug/dL), similar to our simulation data generated under mixture distribution (XG_Mixed). In a bivariate plot overlaying the crude dose–response relationship between blood lead and systolic blood pressure, expected values of blood pressure at 25^th to 75^th percentiles of blood lead were similar across all models; however, the expected values varied substantially at lower and higher tails of blood lead (Figure 3).

Figure 3.

Scatter plot of blood lead (ug/dL) and systolic blood pressure (mmHg) along with regression lines from crude models and vertical lines representing 5^th, 25^th, 50^th, 75^th, and 95^th percentiles of lead.

We estimated associations between box-cox transformed systolic blood pressure and blood lead using four regression models: linear regression, robust linear model, linear regression with quadratic term for blood lead, and linear regression with log-transformed blood lead. For each analytic approach, estimates were obtained with or without adjustment for age (quadratic), gender (male/female[ref]), race/ethnicity (Hispanic/non-Hispanic black/non-Hispanic white[ref]/other), calendar year (linear), waist circumference (linear). We bootstrapped 95% confidence intervals using R package boot (5,000 iterations). When model fit was compared using AIC, the approach with log-transformed lead appeared to perform the best (Table 3). Compared to the analytic approach that best fit the data (i.e., linear regression with log-transformed lead), the expected difference in systolic blood pressure per quartile change in blood lead was lower for all other approaches, particularly at lower and higher tails of blood lead. For example, the fully adjusted model with ln(blood lead) best fit the data (AIC: - 301648.57) as compared to that with untransformed blood lead (AIC: −301635.14); expected difference in systolic blood pressure was higher at lower percentiles of X. However, we note that model fit is a global phenomenon that depends on specification beyond simple transformations. When we modified our approach to allow non-additive effect measure modification by sex, model fit criteria in the stratum of males was best for linear regression using ln(blood lead) while linear regression with untransformed blood lead was best in the stratum of females (Table 4).

Table 3.

Average predicted values of systolic blood pressure at percentiles of blood lead $\left(\overline{p}\left(y|x_q\right)\right)$, marginal difference in predicted systolic blood pressure equivalent to 25 percentile change in the total population $\left(\overline{p}\left(y\mid x_{q1}\right)-\overline{p}\left(y\mid x_{q0}\right)\right.$, where exposure contrast from 50^th to 25^th percentile=0.47 ug/dL and 75^th to 50^thpercentile=0.78 ug/dL), and their model fit by analytic approach in NHANES 1999–2016 (n=23,113)^a

	Regression models
	Linear	Robust	Log-transformed	Quadratic
Crude
AIC	−296581	−296539	−297174	−296814
$\overline{p}\left(y\mid x_{25}\right)$	115.69 (115.41, 115.96)	115.83 (115.56, 116.09)	114.8 (114.55, 115.05)	115.19 (114.86, 115.44)
$\overline{p}\left(y\mid x_{50}\right)$	116.20 (115.98, 116.42)	116.47 (116.26, 116.69)	116.71 (116.49, 116.93)	116.09 (115.87, 116.31)
$\overline{p}\left(y\mid x_{75}\right)$	117.01 (116.77, 117.28)	117.51 (117.27, 117.75)	118.69 (118.41, 118.97)	117.51 (117.26, 117.89)
$\overline{p}\left(y\mid x_{50}\right)-\overline{p}\left(y\mid x_{25}\right)$	0.51 (0.41, 0.63)	0.64 (0.53, 0.76)	1.9 (1.8, 2.1)	0.90 (0.79, 1.13)
$\overline{p}\left(y\mid x_{75}\right)-\overline{p}\left(y\mid x_{50}\right)$	0.82 (0.65, 1.0)	1.0 (0.86, 1.2)	2.0 (1.8, 2.1)	1.4 (1.3, 1.8)
Adjusted for age, gender, race/ethnicity, education, NHANES cycle, waist circumference
AIC	−301635	−301614	−301648	−301635
$\overline{p}\left(y\mid x_{25}\right)$	118.22 (117.96, 118.48)	118.48 (118.24, 118.73)	117.99 (117.69, 118.29)	118.15 (117.84, 118.43)
$\overline{p}\left(y\mid x_{50}\right)$	118.28 (118.04, 118.51)	118.54 (118.32, 118.77)	118.29 (118.07, 118.52)	118.25 (118.01, 118.48)
$\overline{p}\left(y\mid x_{75}\right)$	118.37 (118.14, 118.60)	118.63 (118.42, 118.86)	118.60 (118.34, 118.88)	118.41 (118.18, 118.66)
$\overline{p}\left(y\mid x_{50}\right)-\overline{p}\left(y\mid x_{25}\right)$	0.057 (−0.0061, 0.12)	0.058 (0.0052, 0.11)	0.31 (0.13, 0.48)	0.10 (0.011, 0.22)
$\overline{p}\left(y\mid x_{75}\right)-\overline{p}\left(y\mid x_{50}\right)$	0.092 (−0.0097, 0.20)	0.093 (0.0083, 0.18)	0.31 (0.13, 0.49)	0.16 (0.017, 0.34)

Abbreviations: linear, general linear model (GLM) with untransformed X; robust, robust linear model with untransformed X; log-transformed, GLM with log-transformed X; quadratic, GLM with quadratic term for X; AIC, Akaike information criterion.

^aAdjusted for age, gender, race/ethnicity, education, NHANES cycle, waist circumference and 95% confidence intervals bootstrapped.

Table 4.

Sex-stratified average predicted values of systolic blood pressure at percentiles of blood lead $\left(\overline{p}\left(y|x_q\right)\right)$, marginal difference in predicted systolic blood pressure per change in blood lead equivalent to 25 percentile change in the total population $\left(\overline{p}\left(y\mid x_{q1}\right)-\overline{p}\left(y\mid x_{q0}\right)\right.$, where exposure contrast from 50^th to 25^th percentile=0.47 ug/dL and 75^th to 50^thpercentile=0.78 ug/dL), and their model fit by analytic approach in NHANES 1999–2016 (n=23,113)^a

Model	Parameter	Females (n=11,180)	Males (n=11,933)
Linear	AIC	−145063	−157491
	$\overline{p}\left(y\mid x_{25}\right)$	115.64 (115.26, 116.01)	120.29 (119.94, 120.62)
	$\overline{p}\left(y\mid x_{50}\right)$	115.71 (115.37, 116.05)	120.36 (120.05, 120.66)
	$\overline{p}\left(y\mid x_{75}\right)$	115.82 (115.43, 116.23)	120.48 (120.19, 120.76)
	$\overline{p}\left(y\mid x_{50}\right)-\overline{p}\left(y\mid x_{25}\right)$	0.071 (−0.070, 0.23)	0.073 (0.0049, 0.15)
	$\overline{p}\left(y\mid x_{75}\right)-\overline{p}\left(y\mid x_{50}\right)$	0.11 (−0.11, 0.36)	0.12 (0.0077, 0.23)
Robust	AIC	−145052	−157473
	$\overline{p}\left(y\mid x_{25}\right)$	115.93 (115.56, 116.29)	120.68 (120.35, 120.98)
	$\overline{p}\left(y\mid x_{50}\right)$	116.01 (115.67, 116.34)	120.74 (120.45, 121.02)
	$\overline{p}\left(y\mid x_{75}\right)$	116.14 (115.75, 116.52)	120.85 (120.57, 121.12)
	$\overline{p}\left(y\mid x_{50}\right)-\overline{p}\left(y\mid x_{25}\right)$	0.082 (−0.053, 0.22)	0.068 (0.068, 0.13)
	$\overline{p}\left(y\mid x_{75}\right)-\overline{p}\left(y\mid x_{50}\right)$	0.13 (−0.085, 0.35)	0.11 (0.011, 0.2)
Log-transformed	AIC	−145061	−157501
	$\overline{p}\left(y\mid x_{25}\right)$	115.73 (115.35, 116.10)	119.90 (119.45, 120.33)
	$\overline{p}\left(y\mid x_{50}\right)$	115.73 (115.37, 116.08)	120.29 (119.98, 120.59)
	$\overline{p}\left(y\mid x_{75}\right)$	115.72 (115.25, 116.21)	120.68 (120.37, 120.99)
	$\overline{p}\left(y\mid x_{50}\right)-\overline{p}\left(y\mid x_{25}\right)$	−0.00078 (−0.25, 0.27)	0.39 (0.16, 0.62)
	$\overline{p}\left(y\mid x_{75}\right)-\overline{p}\left(y\mid x_{50}\right)$	−0.00078 (−0.25, 0.27)	0.39 (0.16, 0.63)
Quadratic	AIC	−145061	−157491
	$\overline{p}\left(y\mid x_{25}\right)$	115.61 (115.21, 115.99)	120.18 (119.73, 120.55)
	$\overline{p}\left(y\mid x_{50}\right)$	115.72 (115.37, 116.06)	120.30 (119.95, 120.61)
	$\overline{p}\left(y\mid x_{75}\right)$	115.87 (115.44, 116.34)	120.50 (120.21, 120.79)
	$\overline{p}\left(y\mid x_{50}\right)-\overline{p}\left(y\mid x_{25}\right)$	0.10 (−0.08, 0.33)	0.12 (0.016, 0.27)
	$\overline{p}\left(y\mid x_{75}\right)-\overline{p}\left(y\mid x_{50}\right)$	0.15 (−0.12, 0.49)	0.19 (0.026, 0.42)

Abbreviations: linear, general linear model (GLM) with untransformed X; robust, robust linear model with untransformed X; log-transformed, GLM with log-transformed X; quadratic, GLM with quadratic term for X; AIC, Akaike information criterion.

^aAdjusted for age, gender, race/ethnicity, education, NHANES cycle, waist circumference and 95% confidence intervals bootstrapped.

DISCUSSION

This study demonstrates that a skewed exposure distribution does not necessitate the decision to log-transform exposure, using simulations under eight scenarios that could give rise to skewed X and normal Y. Our simulation results suggest that log-transforming an independent variable can bias effect estimates when the underlying true dose–response relationship is linear (YG_Add), even in the presence of outliers (XG_Mixed). In the absence of other sources of bias (i.e., XG_LogN, XG_Trunc, and XG_Mixed), the analytic approach that best reflected the underlying truth had the best model performance and least biased estimates, regardless of the skewness of the independent variable. In the presence of another bias source (e.g., measurement error in XG_MErr), all approaches yielded biased estimates. Although the true dose–response relationship is always unknown, comparing model fit under different analytical approaches can provide guidance on selecting the model that best represents associations in the analytic dataset. Fit statistics, such as AIC used in our example, can be useful as RMSE and %bias cannot be derived without the truth. Our findings illustrate that the decision to log-transform independent variables should be based on whether such transformation improves model fit statistics compared to alternative model specifications, rather than basing the decision on the distribution of the independent variable.

Although concerns for outlier influences are often reported as motivations to log-transform skewed independent variables, our simulation results comparing estimates by X transformation or robust linear model suggest that outlier influence is a lesser concern than incorrect model specification. Log-transforming X substantially biased expected values of Y and expected values of Y per X contrasts when the underlying true relations were linear, across all data generation methods. Our results are in line with the previously demonstrated finding that using a geometric mean to describe the central tendency of a log-transformed independent variable is not more robust to outliers or precise than the arithmetic mean (13).

We additionally demonstrated a worked example using NHANES to determine the optimal modeling approach for a skewed exposure variable. Rather than defaulting to log-transformation, we compared analytic models with various forms (i.e., original, quadratic, log-transformed). We also assessed effect measure modification and compared alternative analytic approaches (i.e., robust linear model). Although a similar level of skewness was observed across all models, comparing AIC lent support that the model with log-transformed X best fit the data in our example overall and among males only, but not among females only. Importantly, we found that associations were weaker in models that did not fit the data well.

Throughout, we focus on assessing model fit for estimating E(Y|X). A key related concern in linear and generalized linear models is that of the error term and the validity of conventional standard errors depend on accurate specification of the error term distribution. Thus, one might speculate that examining model residuals is also crucial to our endeavor, since it can help uncover phenomena like violations of homoskedasticity (does the variance change with values of predictors) that signal model misspecification. However, we note that in the special case of our g-computation-based estimator (with bootstrap standard errors in the case of our blood lead example), the validity of the estimates does not depend on homoskedasticity of the error term, and only the “mean model” for estimating E(Y|X) need be correctly specified. Thus, in contrast to AIC, which addresses relative goodness of fit for competing mean models, examination of model residuals may yield misleading information about whether one should transform exposures because residuals are impacted by the mean model as well as the error distribution. In the case where one is interested in model parameters, rather than g-computation, an alternative way to address non-normal residuals would be the use of heteroskedasticity-robust standard errors, or bootstrapping. In the case of our blood lead example, one can also address non-normal error term distributions through transformations of the outcome. G-computation gives a framework for easily contrasting implications of different transformations of the data.

A broader contribution of this work is that we demonstrate an approach to assessing whether transformations of independent variables may be needed. Following the original work of Box and Tidwell (7), we focus on how the transformation of independent variables affects overall model fit. Alternative to relying on significance testing of independent variables, our approach to compare the overall fit of models with different exposure transformations more directly addresses the central question of how exposures should be entered into the model. Comparing the size and precision of effect estimates from models with different exposure transformations is typically difficult because transformation fundamentally alters the interpretation of model coefficients. However, our approach of focusing on expected values and contrasts of expected values at specific values of exposure ameliorates this issue and allows direct comparison of the implied effect sizes under each transformation. This approach is also beneficial when different transformations may fit better in subsets of the data, as in our NHANES example: regression coefficients for males and females were not comparable due to different preferred transformations, but the expected contrasts were easily comparable. This approach also benefited interpretability due to our Box–Cox transformation of the study outcome, which would otherwise yield effect measures that do not map directly onto the measured outcome. We note that this approach is a simple form of g-computation, which has wide applicability for use in flexible models (24–26).

When presented with skewed independent variables, defaulting to log-transformation is not a one-size-fits-all approach to resolve potential biases. Rather, it may be more important to apply epidemiologic thinking to speculate on sources of bias and approaches to resolve specific biases identified. For example, log-transforming an independent variable may not fit the data well if the underlying dose–response relationship is non-linear on the log scale (e.g., linear or quadratic on the additive scale), irrespective of the skewness of exposure. Specifically for skewed exposure, a mixture distribution of two distinct populations (non-occupational and occupational sources) could additionally include another source of bias (e.g., healthy worker bias), in which case estimation of dose–response in stratified populations may be more appropriate. Another example that can give rise to skewed exposure is outliers, potentially introduced by measurement error due to factors such as batch effects or urinary dilution, in which case correcting for information bias (27) would be preferable to log-transformation. While not demonstrated in our study, other potential sources of bias (i.e., confounding, selection) can be considered as to whether they can give rise to a skewed distribution of the independent variable and corrected for using appropriate methods rather than log-transforming the independent variable. Last, our findings on X transformation also apply to misspecification of confounders and residual confounding, reinforcing the importance of correct model specification since transformation of independent variables is one of many approaches to improve model fit (28).

CONCLUSION

Findings from our simulation suggest that in general linear models, skewness of an independent variable does not always warrant log-transformation, even in the presence of outliers, and can bias effect estimates at lower and higher tails of the distribution if it does not reflect the underlying true dose–response relationship. Broadly, we recommend that skewed distribution of independent variables should not inform the decision to log-transform exposure, unless such skewness is thought to have arisen from a source of bias. Since the true dose–response relationship is unknown, investigators should consider several analytic models and base their final model selection on a comparison of fit statistics. In our simulations, model fit was correlated with bias, suggesting that the Akaike information criterion may be a useful tool for comparing competing models when the true bias is unknown. If skewed distribution of an independent variable is thought to have arisen from a bias source (e.g., confounder, selection, measurement error), it is important to include in model comparison the analytic models that directly address and ameliorate such bias rather than log-transforming the independent variable.