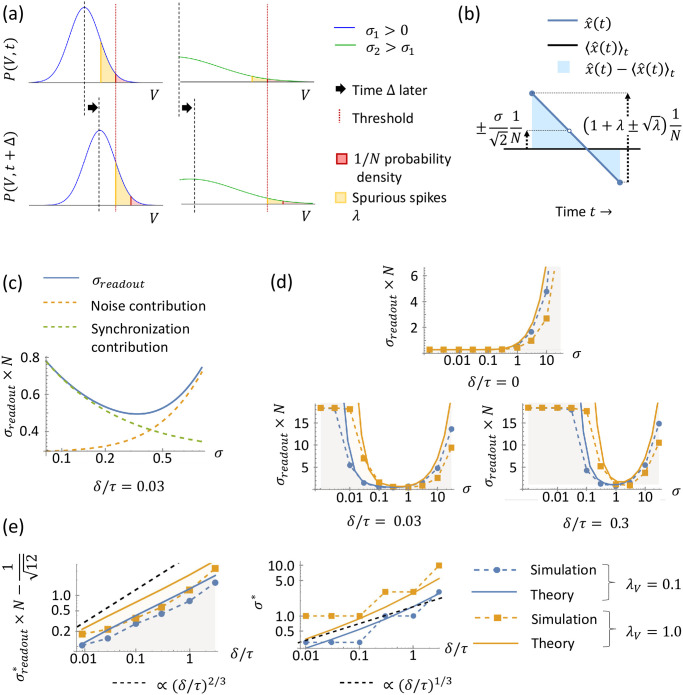
Fig 4. LIF model with nonzero delay.

(a) Calculation of the number of spurious spikes. For a nonzero noise level σ₁, the membrane potentials travel in a Gaussian packet with density P(V, t) (blue, top left) toward threshold (vertical red dotted line). The typical position of the packet at the time t when the first neuron spikes is determined by ensuring the tail probability (red, shaded area) above threshold equals 1/N. During the spike propagation delay Δ, the Gaussian packet continues traveling toward threshold (blue, bottom left), and the mean number of spurious spikes λ is given by the additional probability density that crosses threshold (yellow, shaded area). A larger noise level σ₂ spreads out the Gaussian packet (green, right), thus reducing λ. (b) Readout $\widehat{x}\left(t\right)$ (blue) and its deviation $\widehat{x}\left(t\right)-x\left(t\right)$ (light blue shaded) from the mean ${\langle \widehat{x}\left(t\right)\rangle }_t$. Similar to Fig 3b, the accumulated spike-time variation creates fluctuations in $\widehat{x}\left(t\right)$ with standard deviation upper-bounded by $\frac{\sigma }{\sqrt{2}}\frac{1}{N}$, but in addition, spurious spikes introduce a Poisson variation in the readout with standard deviation $\sqrt{\lambda }\frac{1}{N}$. (c) Integrating the deviations illustrated in (b) yields an approximate upper-bound for σ_readout, Eq 24 (blue). Conceptually, σ_readout receives contributions from noise (Eq 24 without the λ term; yellow, dashed), and synchronous spurious spikes (Eq 24 without the $\frac{{\sigma }^2}{2}$ term; green, dashed). (d) Readout error σ_readout for varying levels of noise. For zero delay (top), noise is not necessary to prevent spurious spikes, and thus it strictly increases σ_readout. For non-zero delays (bottom), σ_readout has a U-shaped dependence on σ, and an optimal noise level σ* exists. The dots/squares on dashed lines represent σ_readout from simulations (N = 64), and solid lines are Eq 24, with the region below shaded, indicating upper-bound. Blue signifies λ_V = 0.1; yellow λ_V = 1.0. (e) Minimal readout error ${\sigma }_{readout}^{*}$ and optimal noise level σ* as a function of delay δ. Minimizing Eq 24 (with higher-order terms, see Eq S91 in S1 Appendix) with respect to σ yields ${\sigma }_{readout}^{*}$ (left, solid lines) and σ* (right, solid lines). ${\sigma }_{readout}^{*}-\frac{1}{\sqrt{12}}$ and σ* asymptotically approach (δ/τ)^2/3 and (δ/τ)^1/3, respectively (dashed black lines). We take the minimal σ_readout from the simulations in (d) and the associated optimal noise level to generate the dots/squares on the blue/yellow dashed lines, observing that our theory indeed provides an upper-bound for ${\sigma }_{readout}^{*}$ and a good estimate for the optimal noise level σ* in finite-sized simulations.