First-Principles Study of Induced Magnetism in Tungsten Vanadium Selenide Alloys for Spintronic Applications

Abstract

The possibility of inducing magnetization in tungsten selenide monolayer by alloying with vanadium selenide was investigated through first-principles calculations. Electronic, optical, and magnetic properties of different W_1–xV_xSe₂ alloy compositions were studied extensively. As the proportion of vanadium atoms in the alloys increased, a phase transition from semiconducting to metallic to semiconducting was discovered. All alloy compositions demonstrated induced magnetism with a long-range ferromagnetic order. Interestingly, in the case of the W_0.25V_0.75Se₂ alloy, spin-up states in the band diagram showed a finite band gap, while a nonzero band gap was found for spin-down states. The W_0.25V_0.75Se₂ alloy can be used as a spin filter tunneling barrier exploiting this fascinating property. High spin polarization of the tunnel current was found for the alloy. Furthermore, under the Curie temperature, electrical conductivity for the spin-up channel was found to be zero, while conductivity for the spin-down channel was around 10¹⁹ (Ω cm s)⁻¹ when the chemical potential was 0.2 eV greater than the Fermi energy. Changes in optical properties were also investigated through time-dependent density functional theory calculations. The findings of this study will be beneficial for proposing new magnetic monolayer alloys for application in nanoscale spintronic devices.

1. Introduction

Transition metal dichalcogenides (TMDs) have recently garnered much attention among the scientific community due to their intriguing physical, chemical, electronic, and optical properties. Much of the research have been focused on monolayer TMDs constructed from group 6 (VIB) materials, such as WS₂, WSe₂, MoS₂, and MoSe₂. They are direct band gap semiconductors with excellent electronic and optical properties, which make them viable candidates for electronic,¹ photonic,² optoelectronic,^3,4 and valleytronic devices .⁵ However, in most cases, defect-free pristine TMDs are nonmagnetic because there are no unsaturated bonds and no magnetic elements. This nonmagnetic nature prevents their spintronic applications.

During the growth process edges, dislocations, grain boundaries, and other imperfections may occur which alter the electronic and magnetic properties of the TMDs. Chalcogen vacancies in WSe₂ monolayers introduced changes in electronic properties, such as band gap narrowing and increase of electron–hole effective masses.⁶ Moreover, it was reported that induced magnetism in defected monolayer WSe₂ was found as a result of two W atom vacancies.⁷ Structural defects such as vacancies are intrinsically generated in as grown WSe₂ monolayers .⁸ However, achieving proper growth control of magnetism inducing defects in TMDs through structural engineering methods can be very difficult.

Although VSe₂ exists only in the T phase in nature, T to R polytype transformation have been observed through Cu deposition in thin VSe₂ surface layers or by intercalating Cu into bulk VSe₂ .⁹ H-type single layer components were found in the R polytype VSe₂ bulk as the only difference between H-WSe₂ and R-VSe₂ is the stacking patterns of sandwich layers. From first-principles calculation, monolayer 1H-VSe₂ was found to be a ferromagnetic (FM) semiconducting material,¹⁰ whereas monolayer WSe₂ is a nonmagnetic semiconductor with a direct band gap .⁶ Previously, there have been reports of vanadium-doped WSe₂ behaving as dilute magnetic semiconductors .^11,12 However, doping TMDs may suffer from several disadvantages, such as alteration of the lattice structure, formation of defects or dislocations, and reduced mobility due to different scattering mechanisms. In contrary, growth of highly pure crystals of W_0.75V_0.25Se₂ and W_0.25V_0.75Se₂ alloy was demonstrated through the direct vapor transport technique .^13,14 These alloys showed excitonic resonances and fast rise and decay of photo current, efficient absorption for photodetection applications. However, the possibility of creating monolayer FM semiconducting material through tungsten vanadium selenide alloys has yet to be explored.

In this work, we explored the possibility of inducing magnetism in monolayer WSe₂ by alloying it with VSe₂ using first-principles calculations. By alloying in different compositions, interesting changes can be found in electronic and magnetic properties from their pristine crystals. To comprehend how the lattice structure changes with alloying, we reported the optimized ground state structure found through density functional theory (DFT) calculations. Electronic and magnetic properties such as spin-polarized E-k diagram with and without spin–orbit coupling (SOC), orbital projected band diagram (fatbands), projected density of states (PDOS), charge density difference, Bader charge transfer, total magnetism, and magnetism distributions were analyzed for different alloy compositions. Our investigation of inducing long-range magnetic order in 2D TMDs through alloying can be vital for future spintronic devices. Additionally, spin-polarized splitting of conduction bands were studied. Ferromagnetic semiconductors showing exchange splitting of conduction bands in the magnetically ordered state can be used as spin filter tunneling barriers¹⁵ in spin filter transistors .¹⁶ To investigate the spin-filtering capability of W_1–xV_xSe₂ alloys, spin polarization of tunnel current and temperature-dependent spin-polarized electrical conductivity was calculated. Additionally, we studied optical properties by utilizing time-dependent DFT calculations. Exciting electronic, magnetic and optical properties revealed from our study uphold the potential of these alloys in emerging applications.

2. Computational Details

The electronic and magnetic properties of the monolayers were calculated using Quantum ESPRESSO^17,18 which is based on DFT. Projector augmented wave (PAW) pseudopotentials of tungsten, vanadium, and selenium were used with exchange–correlation functional described by the Perdew–Burke–Ernzerhof (PBE) functional within the generalized-gradient approximation (GGA). Marzari-Vanderbilt-DeVita-Payne cold smearing¹⁹ of 0.01 Ry was used to describe the electron occupations. Kinetic energy cutoff of 50 Ry was used for electron wave functions and kinetic energy cutoff of 500 Ry was used for charge density and potential. Structural relaxation were performed until forces on atoms converged down to 10^–3 Ry/Bohr and minimum difference in total energies were less than 10^–8 Ry. A (8 × 8 × 1) Γ-centered Monkhorst–Pack grid was used for spin-polarized self-consistent field calculations. Non-self-consistent field calculations were performed using a (32 × 32 × 1) k-point grid to get the density of states (DOS). E-k diagrams were computed along the Γ–M–K−Γ path of the first Brillouin zone and 20 k-points were calculated between each high symmetry points. To observe the effect of SOC, band diagrams for pristine WSe₂, VSe₂, and alloy monolayers were also calculated using fully relativistic PAW pseudopotentials of W, V, and Se atoms with the GGA-PBE exchange–correlation functional.

A (2 × 2 × 1) supercell of monolayer WSe₂ with hexagonal symmetry was created using lattice parameters which matches with experimentally determined crystal structure.²⁰ A vacuum region of 15 Å was added along the z-axis to avoid van der Waals interaction between the periodic images of the monolayers. Pure VSe₂ (V₄Se₈ supercell) and the subsequent alloys—W_0.75V_0.25Se₂ (W₃VSe₈ supercell), W_0.5V_0.5Se₂ (W₂V₂Se₈ supercell), and W_0.25V_0.75Se₂ (WV₃Se₈ supercell)—were created from the (2 × 2 × 1) supercell of 1H-WSe₂ (W₄Se₈ supercell) monolayer by replacing W atom(s) with V atom(s). All the crystal structures were optimized using variable cell relaxation but allowing only x and y components of the cell to change, thus constraining the vacuum region along the z-axis.

The projection of W, V, and Se atomic orbitals on the band dispersion and density of states were determined using Quantum ESPRESSO simulation package. Bader charge analysis for charge distributions in the atoms was conducted using the code developed by the Henkelman group.²¹ Furthermore, temperature-dependent electrical conductivity was calculated using the BoltzTraP code²² within the limitations of the Boltzmann theory and constant relaxation time approximation (see the Supporting Information for details). The calculations were performed on top of the ground state DFT calculation from Quantum ESPRESSO using a dense (32 × 32 × 1) k-point grid.

Ground state electronic structure calculations for the optical properties were done in Quantum ESPRESSO using norm-conserving pseudopotentials with PBE exchange–correlation functional. Optical properties were calculated by solving the Dyson equation²³ within the time-dependent DFT formalism as implemented in the YAMBO code.²⁴ After convergence testing, response block size of the dielectric matrix was taken as 3 Ry. The energy cutoff for expanding the wave functions was taken as 3 Ry. A total of 40 bands were taken for summing over the states in the random phase approximation response function. From the calculated complex dielectric constant, we obtained complex refractive index spectra which were used to calculate reflectance, transmittance, and absorption coefficient of all the monolayers (see the Supporting Information for details).

3. Results and Discussion

Pristine WSe₂, VSe₂, and their derivative alloys (W_0.75V_0.25Se₂, W_0.5V_0.5Se₂, and W_0.25V_0.75Se₂) were optimized and their lattice constants, bond lengths, and bond angles were thoroughly investigated to determine the effect of alloying on the structural properties (see Table 1). Pristine VSe₂ and the monolayer alloys were found to be dynamically stable as can be seen from Figure S1 of the Supporting Information. Pristine structures along with structures with different compositions of V and W are illustrated in Figure 1a–f.

Table 1. Effect of Alloying on the Structural Parameters.

crystal structures	lattice constant	bond length (Å)		bond angle
	a = b (Å)	W-Se	V-Se	∠Se-W-Se	∠Se-V-Se
WSe2 (W4Se8)	6.638	2.547		82.39°
W0.75V0.25Se2 (W3VSe8)	6.649	2.542	2.506	80.83°	82.26°
		2.549		82.32°
W0.5V0.5Se2 (W2V2Se8)	6.677	2.533	2.542	79.94°	79.95°
		2.542	2.499	80.69°	82.04°
W0.25V0.75Se2 (WV3Se8)	6.661	2.537	2.501	79.78°	79.98°
			2.512		80.71°
VSe2 (V4Se8)	6.688		2.508		79.32°

Figure 1.

Optimized structures of different monolayers: (a) pristine WSe₂ (W₄Se₈ supercell), (b) pristine VSe₂ (V₄Se₈ supercell), (c,d) W_0.75V_0.25Se₂ alloy (W₃VSe₈ supercell), (e) W_0.5V_0.5Se₂ alloy (W₂V₂Se₈ supercell), and (f) W_0.25V_0.75Se₂ alloy (WV₃Se₈ supercell). Lattice constants, bond lengths, and bond angles are illustrated here.

As the composition of the V atom was increased, lattice constant also increased. Bond length between the V and Se atom was generally smaller than bond length between W and Se atoms in the crystal structures. This was due to the fact that V had one less valence electron in the d subshell than W. In the W_0.75V_0.25Se₂ alloy, the W-Se bond length was larger when the Se atom was shared only with W atoms and became smaller when Se was shared with a V atom. The same trend was observed in the W_0.5V_0.5Se₂ alloy where the W-Se bond length decreased further when the Se atom was shared only with V atoms. The angle created by Se, W, and Se atoms, ∠Se-W-Se, in the pristine WSe₂ monolayer was found to be 82.39°. For the case of pristine VSe₂ monolayer, ∠Se-V-Se was 79.32°. Both ∠Se-W-Se and ∠Se-V-Se angles in the alloys were smaller than ∠Se-W-Se of pure WSe₂. This deviation arose from the addition of V atoms. The upper and lower Se layers tended to move toward the transition metal layer when V atoms were added. Hence, the lattice constant was larger in the alloys compared to WSe₂.

To determine the energetic stability of the considered systems, formation energy was calculated using total energy of (2 × 2 × 1) supercells of pristine and alloy monolayers computed from DFT study. Formation energy for the alloy monolayers were determined using the equation

1

Here, E_formation is the formation energy of the alloys, E_W1–xVxSe2 represents total energy of alloy monolayer, where x = 0.25, 0.5, and 0.75. and 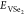are total energies of pristine WSe₂ and VSe₂ monolayers, respectively. Calculated formation energies are shown in Table 2.

Table 2. Formation Energy of W_1–xV_xSe₂ Alloy Monolayers.

crystal structures	formation energy (eV)
W0.75V0.25Se2	0.0494
W0.5V0.5Se2	0.0847
W0.25V0.75Se2	0.0812

Formation energy for all the alloys was positive and had a very small value less than 0.1 eV. As the formation energy is positive, external factors such as temperature or pressure will be required to form the alloy monolayers from pristine monolayers. Among the alloys, W_0.75V_0.25Se₂ had the lowest formation energy and the formation energy was higher for higher vanadium compositions. The formation energy is comparable to other monolayer TMD alloys such as Mo_1–xV_xS₂ and Mo_1–xCr_xS₂ .²⁵

Spin-polarized band diagram with and without including SOC for WSe₂, W_0.75V_0.25Se₂ (W₃VSe₈ supercell), W_0.5V_0.5Se₂ (W₂V₂Se₈ supercell), and VSe₂ monolayers are shown in Figure 2. Without SOC, the pristine WSe₂ monolayer was found as a semiconductor with a direct band gap of 1.55 eV which matched well with previous reports.^6,7 Spin-up and spin-down bands were degenerate resulting in zero magnetic moment for this structure. With SOC, a large splitting of 0.467 eV was found at the valence band maximum (VBM) between spin-down and spin-up states in WSe₂. This is consistent with previous report.²⁶ Splitting was also noticeable in the conduction band minimum (CBM). However, the amount of splitting was much smaller compared to VBM. The direct band gap after including SOC was found to be 1.26 eV (compared to 1.55 eV without SOC) which is consistent with previously reported value.²⁷ In the case of the pristine 1H-VSe₂ monolayer, an indirect band gap of 0.234 eV was observed without SOC, which is consistent with the previous report .²⁸ To find the most stable magnetic order, total energies for both FM and anti-FM (AFM) cases were computed for VSe₂ using a (4 × 4 × 1) supercell. Total energy for FM case was less than total energy for the AFM case (see the Supporting Information). Hence, it can be concluded that monolayer VSe₂ is a FM semiconducting material. Total magnetization of the V₄Se₈ supercell was 4.00 μ_B. VBM occurred at K point originating from a spin-up state and CBM occurred between Γ and K points originating from a spin-down state. After including SOC, two spin-up bands and two spin-down bands below the Fermi level underwent a small amount of splitting along the Γ–M path. Similarly, two spin-down bands above the Fermi level showed splitting along the same k-path. Expectation value of the spin operator along [001] direction was maximum (spin-up, +1/2) or minimum (spin-down, −1/2) around the Fermi level as can be seen from Figure 2h where blue and red lines represent spin-up and spin-down bands, respectively. Separation in spin-up states and spin-down states confirms the presence of magnetic moment after including SOC. Total magnetization was similar to without SOC case, which is evident from the similar positions of spin-up and spin-down bands in both cases.

Figure 2.

Spin-polarized band diagram without SOC for different monolayers: (a) WSe₂ (W₄Se₈ supercell), (c) W_0.75V_0.25Se₂ (W₃VSe₈ supercell), (e) W_0.5V_0.5Se₂ (W₂V₂Se₈ supercell), and (g) VSe₂ (V₄Se₈ supercell). Spin-up and spin-down bands are represented by blue and red lines, respectively. Band diagram including SOC for (b) WSe₂, (d) W_0.75V_0.25Se₂, (f) W_0.5V_0.5Se₂, and (h) VSe₂. The color gradient from blue to red represents expectation values of the spin operator along [001] direction ranging from +1/2 to −1/2.

To find the ground state magnetic ordering of the alloys, both FM and AFM magnetic configurations were considered using (4 × 4 × 1) supercells of monolayer alloys. Total energy for FM configurations was found to be lower than AFM configurations (see the Supporting Information for details). Our calculation showed that magnetic moment contribution from each V atom of any particular monolayer was identical for various sizes of supercells. Hence, all the alloys demonstrated long-range FM order with different total magnetization. For W_0.75V_0.25Se₂, Fermi level shifted inside the valence band. This suggests that this alloy will show a metallic behavior. A total magnetization of 0.38 μ_B/cell was observed for this structure. As the concentration of V was increased in W_0.5V_0.5Se₂, total magnetization increased to 1.53 μ_B/cell. Fermi level moved further into the valence band. Atomic orbital projected DOS without SOC for pristine WSe₂, VSe₂, and the alloys are presented in Figure 3. PDOS of WSe₂ indicated that d orbitals of W atoms contributed significantly in the bands near Fermi level as can be seen in Figure 3a. Similarly, for VSe₂, states around the Fermi level mostly originated from d orbitals of V atoms. For W_0.75V_0.25Se₂ and W_0.5V_0.5Se₂ alloy, states around CBM and VBM were found to be originating from both W-d and V-d orbitals. Though difference in DOS originating from W-d orbitals and V-d orbitals was not much in W_0.75V_0.25Se₂, for W_0.5V_0.5Se₂, a stark increase of V-d orbital states was seen, especially around the CBM. Specific d orbital contributions were investigated in detail and elaborated later (see Figure 4). Similar kind of trend could be seen in case of W_0.25V_0.75Se₂ alloy. For this alloy, an increased total magnetization of 2.97 μ_B/cell was observed. Spin-up and spin-down bands became further separated. The magnetization originated from V atoms and as the percentage of V atom was increased in the alloys, total magnetization also increased. Total magnetization found in the monolayers is summarized in Table 3. Positions of spin-up and spin-down bands in the monolayer alloys after including SOC were similar to their without SOC cases, resulting in similar total magnetization with and without SOC. However, splitting between the spin-up and spin-down bands changed. In the case of W_0.75V_0.25Se₂, energy difference between the two spin-up and spin-down bands above the Fermi level at K point increased from 0.07 eV (without SOC) to 0.4 eV (with SOC), as can be seen from Figure 2c,d. The spin-up band shifted down toward the Fermi level, while the spin-down band shifted upward. This characteristic is similar to splitting of VBM in pristine WSe₂. This was expected as both spin-up and spin-down states above the Fermi level at K point in W_0.75V_0.25Se₂ originated mostly from d_x²–y² (26.7%) and d_xy (26.7%) orbitals of W atoms (see Table 4 and Figure S3 of the Supporting Information). In the case of W_0.5V_0.5Se₂ and W_0.25V_0.75Se₂ (see the Supporting Information for band diagram of W_0.25V_0.75Se₂ with SOC), splitting of bands after including SOC was mostly observed along the Γ–M path similar to pristine VSe₂. This can be attributed to the fact that d orbitals of V atoms contributed more than d orbitals of W atoms around the Fermi level in these alloys. As the overall band structures of pristine VSe₂, WSe₂, and the alloys were similar for with SOC and without SOC cases, orbital projection of band structure and DOS were performed for the without SOC case, which is enough to give a detailed description of the electronic properties.

Figure 3.

PDOS without including SOC for different monolayers: (a) WSe₂ (W₄Se₈ supercell), (b) W_0.75V_0.25Se₂ (W₃VSe₈ supercell), (c) W_0.5V_0.5Se₂ (W₂V₂Se₈ supercell), and (d) VSe₂ (V₄Se₈ supercell). Spin-up and spin-down components of the PDOS are marked by blue and red arrows, respectively.

Figure 4.

Orbital projected E-k diagrams and PDOS without SOC for (a) WSe₂ (W₄Se₈ supercell), (b) VSe₂ (V₄Se₈ supercell), and (c,d) W_0.5V_0.5Se₂ (W₂V₂Se₈ supercell). Spin-up and spin-down bands are grouped together in the E-k diagrams. In the E-k diagrams, size of the circles indicate amount of contribution. Only d orbitals of W and V atoms are shown as they have the most significant contributions around the Fermi level. Spin-up and spin-down components of the PDOS are marked by blue and red arrows, respectively.

Table 3. Magnetization Induced in W_1–xV_xSe₂ Monolayers.

crystal	total magnetization
structures	(per cell)
WSe2(W4Se8 supercell)	0.0 μB
W0.75V0.25Se2(W3VSe8 supercell)	0.38 μB
W0.5V0.5Se2(W2V2Se8 supercell)	1.53 μB
W0.25V0.75Se2(WV3Se8 supercell)	2.97 μB
VSe2(V4Se8 supercell)	4.00 μB

Table 4. d Orbital Contributions of W and V Atoms in the Pristine Crystals and Their Alloys.

monolayer	contribution at VBM				contribution at CBM
	W-dx2–y2	W-dxy	V-dx2–y2	V-dxy	W-dz2	V-dz2	V-dx2–y2	V-dxy
WSe2	37.6%	37.6%			81.2%
W0.75V0.25Se2	26.7%	26.7%	12.3%	12.3%	31.5%	44.3%
W0.5V0.5Se2	13.6%	22.0%	27.2%	17.8%	21.0%	56.4%
W0.25V0.75Se2	6.3%	6.3%	36.8%	36.7%	9.7%	74.7%
VSe2			44.0%	44.0%		35.2%	32.4%	10.8%

For detailed analysis of the electronic properties, projection of atomic orbitals was performed on the band structure and DOS. The d orbitals of W and V atoms predominantly contributed to the bands near the Fermi level. Figure 4a–d shows their contributions for the different crystal structures. Contributions from the other orbitals are provided in the Supporting Information. For WSe₂, VBM consisted primarily of d_x²–y² (37.6%) and d_xy (37.6%) orbitals of W atoms. Other orbital contributions came from p_x (10.4%), p_y (10.4%) orbitals of Se atoms and p_x (1.2%), p_y (1.2%) orbitals of W atoms. On the other hand, CBM consisted primarily of d_z² (81.2%) orbitals of W atoms. Rest of the contribution came from s (11.2%) orbitals of W atoms and p_x (3.2%) and p_y (3.2%) orbitals of Se atoms. For VSe₂, VBM consisted primarily of d_x²–y² (44.0%) and d_xy (44.0%) orbitals of V atoms. Other orbital contributions came from p_x (5.6%), p_y (5.6%) orbitals of Se atoms. Unlike WSe₂, CBM of VSe₂ occurred in between the Γ and K point. It consisted primarily of d_z² (35.2%), and d_xy (32.4%) orbitals of V atoms. Rest of the contribution came from d_x²–y² (10.8%) of V atoms, p_z (10.4%) orbitals of Se atoms, s (2.4%) orbitals of V atoms, and p_x (1.6%) orbitals of Se atoms.

As majority of the contribution at VBM and CBM came from d orbitals of W and V atoms, their projection on the bands is shown for the W_0.5V_0.5Se₂ alloy in Figure 4c,d. Fermi level rested inside the valence band. Due to the upward shift of valence bands, there were one empty spin-up and two empty spin-down states in the K direction. The VBM and CBM both occurred at K point with a gap of 0.539 eV. In VBM, d_x²–y² and d_xy orbitals of V atoms contributed a total of 45.0%. On the other hand, d_x²–y² and d_xy orbitals of W atoms contributed a total of 35.6%. In CBM, d_z² orbital of V atoms contributed 56.4%, whereas d_z² orbitals of W atoms contributed 21.0%. This clearly shows that d orbitals of V atoms have more dominant presence in valence and conduction band edges than the W atoms. This trend was also seen in the other compositions of the W_1–xV_xSe₂ alloy. Table 4 summarizes the orbital contributions at VBM and CBM of different alloy compositions. Orbital projected DOS for d orbitals of W and V atoms of W_0.5V_0.5Se₂ (W₂V₂Se₈ supercell) alloy is shown in Figure 4c,d. Spin-up and spin-down DOS diagrams were found to be asymmetrical for d orbitals of both W and V atoms. The asymmetry was higher for the case of d orbitals of V atoms. Spin-up and spin-down states above the Fermi level and around the band edges were dominated by d orbitals of V atoms.

Spin-polarized E-k diagram along with PDOS of W, V, and Se atoms of W_0.25V_0.75Se₂ (WV₃Se₈ supercell) is shown in Figure 5a. There was a direct band gap of 0.8 eV between spin-up states in the conduction and valence band, while there was no gap between occupied and unoccupied spin-down states. This opens up the opportunity to use W_0.25V_0.75Se₂ as a spin-filter tunneling barrier. During the tunneling process, spin is conserved. Spin-down electrons should not face any barrier during tunneling because of available unoccupied states. However, spin-up electrons see a barrier of 0.8 eV during tunneling. This could give rise to a highly spin-polarized current filtering out spin-up electrons using spin filter effect. This effect is shown schematically in Figure 5b. From the PDOS, it was evident that spin-down states between the band gap of spin-up states mostly came from d orbitals of V atoms. Figure 5c,d shows contributions of d orbitals of W and V atoms. V-d_z², V-d_xy, and V-d_x²–y² orbitals mostly contributed to the spin-down states located between the mid gap of spin-up CBM and VBM states.

Figure 5.

(a) Spin-polarized E-k diagram and PDOS without SOC for the W_0.25V_0.75Se₂ (WV₃Se₈ supercell) alloy. (b) Schematic arrangement of W_0.25V_0.75Se₂ as a spin-filter tunneling barrier between two metal electrodes. (c,d) Projection of d orbitals of W and V atoms on the band diagram and DOS without SOC for the W_0.25V_0.75Se₂ alloy. In the E-k diagrams, size of the circles signify the amount of contribution.

In the metal/W_0.25V_0.75Se₂/metal structure shown in Figure 5b, when electrons with random spin polarization tunnel from the left metal through the W_0.25V_0.75Se₂ spin-filter, spin-up electrons get filtered out because of the gap present in spin-up channel. On the other hand, spin-down electrons can tunnel through the filter easily and a highly spin-polarized current with a large number of spin-down electrons is found in the right metal electrode. The barrier height for spin-up states, Φ_↑, was found to be 0.8 eV, while the barrier height for the spin-down state, Φ_↓, was 0 eV. For a fixed barrier thickness, spin-up tunnel current density, J_↑, and spin-down tunnel current density, J_↓, depend exponentially on the corresponding Φ_↑(↓) as the relation given by²⁹

2

Here, the exchange splitting, which is difference in barrier heights of spin-up and spin-down electrons, was Φ_↑ – Φ_↓ = 0.8 eV. This resulted in a very high spin polarization of the tunnel current, P = 42% obtained from the equation

3

EuO, EuS, and EuSe were reported to exhibit spin filtering behavior with less exchange splittings .^15,30,31 In these materials, spin-up electrons had lower barrier height than spin-down electrons. Therefore, in contrast to W_0.25V_0.75Se₂, spin-down electrons would be filtered out instead of spin-up electrons in these materials.

The condition of spin-filtering was still present after including SOC in W_0.25V_0.75Se₂. The band diagram of W_0.25V_0.75Se₂ with SOC is shown in the Supporting Information. After incorporating SOC, two spin-down bands touching each other at K point just above the Fermi level underwent a splitting of 0.11 eV. The VBM for spin-up state shifted slightly downward increasing the barrier height for spin-up channel from 0.80 eV (without SOC) to 0.88 eV (with SOC). This resulted in an increase in spin-polarization of tunnel current from 42% (without SOC) to 44% (with SOC).

Curie temperature, T_C, can be obtained using the mean field expression³²

4

Here, N is the number of magnetic ions in the magnetic unit cell, k_B is the Boltzmann constant, E_AFM is the total energy in AFM state, and E_FM is the total energy in the FM state. T_C of W_0.25V_0.75Se₂ was estimated to be 59.57 K. The magnetic configurations and total energies are provided in the Supporting Information.

Electrical conductivity relative to relaxation time, σ/τ with respect to chemical potential for WSe₂ and W_0.25V_0.75Se₂ is shown in Figure 6a,b for 50 and 300 K temperature. Details about how the electrical conductivity was calculated are mentioned in the Supporting Information. As WSe₂ was found to be a non-magnetic direct band gap semiconductor, σ/τ for spin-up channel overlapped spin-down channel. σ/τ for both channels dropped sharply above the Fermi energy due to the presence of the band gap. For W_0.25V_0.75Se₂, σ/τ for spin-up channel showed distinct behavior compared to the spin-down channel. When the chemical potential was increased above the Fermi energy, electrical conductivity for spin-up channels dropped sharply and became zero at 0.16 eV for 50 K temperature. However, conductivity for the spin-down channel was around the order of 10¹⁹ (Ω cm s)⁻¹ when chemical potential was above the Fermi energy. Similarly, conductivity for the spin-up channel in W_0.25V_0.75Se₂ dropped sharply above the Fermi energy by an order of 7 in magnitude compared to spin-down channel at 300 K. The spin-up channel introduced a barrier acting as a semiconductor, while the spin-down channel showed metallic characteristics. At 0.43 eV, σ/τ for the spin-up channel was 5.86 × 10¹¹ (Ω cm s)⁻¹, while σ/τ for the spin-down channel was 2.77 × 10¹⁸ (Ω cm s)⁻¹. Thus, the spin-down channel number was significantly greater compared to the spin-up channel number, and consequently, the spin-down channel had a huge conductance. Figure 6c shows the change in spin-up and spin-down conductivity with temperature at a certain chemical potential (μ – E_F = 0.2 eV). Conductivity for the spin-up channel was zero until 60 K and afterward, it started rising with the increase in temperature. Interestingly, spin-up conductivity was always lower than spin-down conductivity which make this alloy particularly functional for spintronic devices.

Figure 6.

Electrical conductivity relative to relaxation time (σ/τ) plotted as a function of chemical potential (μ-E_F) for the spin-up channel (blue curve) and spin-down channel (red curve) for (a) WSe₂ and (b) W_0.25V_0.75Se₂. Dashed curve represents conductivity at 50 K temperature, while solid curve represents conductivity at 300 K temperature. (c) Change in conductivity with respect to temperature for W_0.25V_0.75Se₂ at μ-E_F = 0.2 eV.

Magnetism distribution of pristine WSe₂, VSe₂, and their alloy compositions was estimated from charge distribution as can be seen in Figure 7. For WSe₂, total magnetization was found to be zero. Hence, magnetism distribution in Figure 7b does not show any spin polarization around the atoms. For W_0.75V_0.25Se₂, only the V atom possessed significant atomic magnetic moment which can be seen from the spin polarization plot in Figure 7c. For W_0.5V_0.5Se₂ and W_0.25V_0.75Se₂, V atoms induced an atomic magnetic moment in W atoms in the same direction of the spin polarization of V atoms. For pristine VSe₂, magnetism distribution showed atomic magnetic moments of V atoms are ferromagnetically ordered, which was consistent with previous report .¹⁰Figure 7 also shows change in induced magnetization with the increase in composition of vanadium. Total magnetic moment of V atoms closely followed the total magnetization curve. Thus, in all the alloy compositions and pristine VSe₂, magnetization mostly originated from atomic magnetic moments of the V atoms.

Figure 7.

(a) Total magnetization and total atomic magnetic moment of V atoms in W_1–xV_xSe₂ monolayers as a function of V atom composition. Magnetism distribution of (b) pristine WSe₂ (W₄Se₈ supercell), (c) W_0.75V_0.25Se₂ (W₃VSe₈ supercell) alloy, (d) W_0.5V_0.5Se₂ (W₂V₂Se₈ supercell) alloy, (e) W_0.25V_0.75Se₂ (WV₃Se₈ supercell) alloy, and (f) pristine VSe₂ (V₄Se₈ supercell). Isosurface value was set to be 0.008 e/Bohr³.

Top view of charge density difference for WSe₂, VSe₂, W_0.75V_0.25Se₂, W_0.5V_0.5Se₂, and W_0.25V_0.75Se₂ alloys are shown in the Supporting Information (see Figure S7). Unlike the pristine structures, the W_0.75V_0.25Se₂ alloy showed an anisotropic behavior in the charge density difference. Though there were regions of depletion around V atoms in pristine VSe₂, for the same isosurface value, the V atom in W_0.75V_0.25Se₂ did not show same region of depletion around itself. In case of W_0.5V_0.5Se₂ and W_0.25V_0.75Se₂, this anisotropic behavior was increased further and new regions of charge accumulation was seen around the V atoms.

Table 5 shows average charge transfer of V, Se, and W atoms in the crystal structures as calculated through Bader charge analysis. It was seen that, charge transfer to Se atoms increased as the composition of V atoms were increased in the alloys. This effect can be attributed to Se layers moving inward to the transition metal layer with alloying as stated before. Charge transfer from V atoms showed less changes compared to Se and W atoms. However, charge density difference plots (Figure S7c–e) showed spatial charge redistribution around the V atoms.

Table 5. Average Charge Transfer from Bader Charge Analysis.

crystal structures	average charge transfer
	V	Se	W
WSe2(W4Se8 supercell)		–0.50947375	+1.01902675
W0.75V0.25Se2(W3VSe8 supercell)	+1.180299	–0.53572675	+1.035342
W0.5V0.5Se2(W2V2Se8 supercell)	+1.184901	–0.565672	+1.0774385
W0.25V0.75Se2(WV3Se8 supercell)	+1.180041	–0.574831375	+1.058224
VSe2(V4Se8 supercell)	+1.19390175	–0.59698425

Optical properties of W_1–xV_xSe₂ alloy monolayers for different compositions were calculated. Calculation details are provided in the Supporting Information. Real and imaginary parts of the complex dielectric constant for pristine monolayers and their consequent alloys are presented in Figure S11 of the Supporting Information. Frequency-dependent refractive index, n, and extinction coefficient, κ, were determined from the complex dielectric constant. The absorption coefficient, α, was determined from the equation, α = 4πκ/λ, where λ is the wavelength of the incident photon. The absorption coefficient, E-k diagram and JDOS for pristine WSe₂ is presented in Figure 8a. Under 1.55 eV, JDOS was close to zero. The absorption edge was found at around 1.55 eV which corresponds to the direct band gap of WSe₂ at K point. α depends on the quantum-mechanical probability of electron transition from filled states of the valence band to empty states of the conduction band. From JDOS, we get the total picture of number of occupied states at E and unoccupied states at E + hν, where hν is the photon energy. Absorption peaks found at higher energy matched with the peaks found in JDOS. For WSe₂, there was a steep increase in α at 2.5 eV. It was due to interband transitions into higher energy levels of the conduction band. W_0.75V_0.25Se₂ and W_0.25V_0.75Se₂ possessed a substantial amount of α in infrared range, as shown in Figure 8. These two alloys also showed the Reststrahlen effect in this range which is described in the Supporting Information. For W_0.5V_0.5Se₂, an absorption edge was found above 0.5 eV. This was due to direct transition between the highest occupied spin-up state and the lowest unoccupied spin-down state at the Γ point. These two bands were parallel and showed similar curvature around the Γ point. A gap of 0.54 eV was present between the bands. The absorption edge for VSe₂ above 0.67 eV was due to direct transition from the highest occupied spin-up band to the lowest unoccupied spin-up band at the K point. Pristine WSe₂ and VSe₂ showed large absorption in the visible light region but the absorption coefficient dropped in the infrared region. However, the alloys showed good absorption both in the infrared region and the visible light region.

Figure 8.

(a) Absorption coefficient, E-k diagram and joint density of states (JDOS) for WSe₂. For the E-k diagram, VBM at K point is set to zero energy. Absorption coefficient for (b) W_0.75V_0.25Se₂, (c) W_0.5V_0.5Se₂, (d) W_0.25V_0.75Se₂, and (e) VSe₂.

4. Conclusions

We studied the effects of alloying on structural, electronic, optical, and magnetic properties of monolayer W_1–xV_xSe₂ using DFT calculations. Alloying the 1H-WSe₂ monolayer with 1H-VSe₂ monolayer introduced changes in the crystal structure and lattice parameter was increased. Because of alloying, a transition from semiconducting (WSe₂) to metallic (W_1–xV_xSe₂) to semiconducting (VSe₂) state was observed. All of the alloys demonstrated induced magnetism. Total magnetic moment increased with the increase of vanadium composition and maximum magnetic moment of 4.0 μ_B/(V₄Se₈ supercell) was reached for VSe₂. By investigating the spin polarization, the pristine 1-H VSe₂ monolayer and all the monolayer alloys were found to be ferromagnetically ordered. W_0.25V_0.75Se₂ alloy showed unique spin filtering characteristics. In W_0.25V_0.75Se₂, a gap of 0.8 eV opened for the spin-up channel, while the spin-down channel showed no gap around the Fermi level. Because of this barrier, 42% spin polarization was found in the tunnel current without incorporation of SOC. Below the Curie temperature, electrical conductivity for the spin-down channel was around 10¹⁹ (Ω cm s)⁻¹, while the spin-up channel showed zero electrical conductivity when the chemical potential was 0.2 eV above the Fermi energy. These properties can be exploited to create spin filter tunnel junctions in spin filtering transistors. Investigation of the optical properties revealed good absorption of alloy monolayers in the infrared region which was not present in pristine WSe₂ and VSe₂ monolayers. Our results will provide direction for utilizing FM monolayer TMD alloys which could be useful in designing novel spin-electronic devices.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c03312.

• Dynamical stability of pristine VSe₂ and monolayer alloys; band diagram of W_0.25V_0.75Se₂ with and without SOC; total magnetization with and without SOC; orbital projected band diagram and density of states for d orbitals of W and V atoms in W_0.75V_0.25Se₂ and s, p orbitals of Se, W, and V atoms in pristine WSe₂, pristine VSe₂, and monolayer alloys; molecular orbitals for WSe₂, VSe₂, and W_0.25V_0.75Se₂; charge density difference isosurfaces; ground state magnetic order; Curie temperature calculation; details of electrical conductivity calculation; and complex dielectric constant, complex reflective index, transmittance, and reflectance of pristine and alloy monolayers (PDF)

The authors declare no competing financial interest.