Phase and polarization modulation in two-dimensional In₂Se₃ via in situ transmission electron microscopy

Abstract

Phase transitions in two-dimensional (2D) materials promise reversible modulation of material physical and chemical properties in a wide range of applications. 2D van der Waals layered In₂Se₃ with bistable out-of-plane ferroelectric (FE) α phase and antiferroelectric (AFE) β′ phase is particularly attractive for its electronic applications. However, reversible phase transition in 2D In₂Se₃ remains challenging. Here, we introduce two factors, dimension (thickness) and strain, which can effectively modulate the phases of 2D In₂Se₃. We achieve reversible AFE and out-of-plane FE phase transition in 2D In₂Se₃ by delicate strain control inside a transmission electron microscope. In addition, the polarizations in 2D FE In₂Se₃ can also be manipulated in situ at the nanometer-sized contacts, rendering remarkable memristive behavior. Our in situ transmission electron microscopy (TEM) work paves a previously unidentified way for manipulating the correlated FE phases and highlights the great potentials of 2D ferroelectrics for nanoelectromechanical and memory device applications.

A set of phase and polarization modulations are achieved in 2D In₂Se₃ by in situ transmission electron microscopy.

INTRODUCTION

Controlling the phases of matter is a central task for materials science. By means of phase engineering, improved performances (1–3) and extended functionalities (4) have been achieved in bulk materials. In recent years, with the exciting discovery and development of two-dimensional (2D) materials (5–8), numerous new phases were unveiled in 2D, because of their reduced dimension (9, 10). Phase transition in 2D has been frequently found in many 2D polymorphic materials (11–13). For example, by modulating the 1T′ and 2H phases in 2D MoTe₂ with an optical laser, better electrical contacts can be rendered (11). On the basis of the electrically stimulated phase transition, resistive memory can be made in 2D MoTe₂ (14), PdSe₂ (15), TaS₂ (16), etc., showing great potential for next-generation digital memory and neuromorphic computing (17, 18). The prevailed 2H-1T and 2H-1T′ phase transitions in 2D transition metal dichalcogenides can also be triggered by alkali metal intercalation, which is beneficial for the electrocatalytic performances of these materials (19). Structural phase transitions aside, arising from the reduced dimension, a variety of new physical characteristics emerged in 2D materials, such as ferroelectrics (20, 21), ferromagnetics (22, 23), superconductivity (24, 25), etc., which correlate with the phase transition in 2D materials, are currently under intensive study.

Recently, 2D van der Waals (vdW) layered In₂Se₃ has attracted much attention because of its multiferroic nature, e.g., ferroelectricity and ferroelasticity, in different phases (21, 26, 27). α-In₂Se₃ is a ferroelectric (FE) phase with out-of-plane ferroelectricity (21, 28), while β′-In₂Se₃ was reported as an in-plane FE phase with thickness down to 45 nm (27) and recently has been confirmed as antiferroelectric (AFE) phase (26). As a result of the bistable coexistence of AFE β′ phase and out-of-plane α phase in 2D In₂Se₃, it is hopeful to use this AFE and out-of-plane FE phase transition for potential applications such as next-generation transistor and nonvolatile logic devices (29). Experimentally, it has been reported that the 2D α-In₂Se₃ can transform into β′-In₂Se₃ by increasing the temperature from room temperature to 220°C (26) or 290°C (30); however, β′-In₂Se₃ cannot return to α-In₂Se₃ when the temperature drops back to room temperature, showing the difficulty in controlling the phases of 2D In₂Se₃ solely by the thermal effect. In addition, electric field can induce the reversible phase transition between β′ phase and the nonlayered γ phase in In₂Se₃ for memristor applications (31). On the theory side, density functional theory (DFT) calculations have predicted the phase transition in monolayer (one quintuple layer) α-In₂Se₃, namely, the strain triggered topological phase transition in 1L α-In₂Se₃ (32). Despite these efforts above, a complete and reversible phase transition in 2D In₂Se₃ still largely remains unclear, especially the reversible phase transition between FE α phase and β′ phase of interest has not been achieved.

Here, using chemical vapor deposition (CVD)–synthesized 2D β′-In₂Se₃, we reveal thickness-dependent phase stability in few-layer samples. When the number of 2D β′-In₂Se₃ layers decreases below four, the β′-In₂Se₃ spontaneously transforms into α-In₂Se₃. In addition, temperature is the conventionally dominated mode to control phase transition in bulk In₂Se₃. With the rising temperature, α, β, and γ bulk phase sequentially dominates in In₂Se₃ (33, 34), while in their 2D counterparts, AFE β′-In₂Se₃ emerges and competes with the out-of-plane FE α phase at the room temperature. As we present here, the phase stability of α and β′ phases in 2D In₂Se₃ can be controlled by strain or thickness in addition to temperature, and these previously undefined paths for phase control offer rich opportunities in 2D ferroelectrics. We apply comprehensive in situ TEM on 2D In₂Se₃ and confirm the phase manipulations through mechanical and electrical stimuli (scheme shown in Fig. 1A). The reversible FE phase transition between α-In₂Se₃ and β′-In₂Se₃ is first-time reported, enabled by strain manipulation. Moreover, through the local joule-heating effect, phase transition from α-In₂Se₃ to β′-In₂Se₃ and γ-In₂Se₃ can be realized. We further show that the intrinsic polarizations can be readily controlled by external electric field in 2D FE phases. These results offer a versatile platform for manipulating and engineering the phases and polarizations in 2D FE materials, which will promote the development of 2D FE devices.

Fig. 1. Phase evolutions and thickness dependence of 2D In₂Se₃.

(A) Atomic scheme of the phase transitions in 2D In₂Se₃. (B) Phase diagram of α-In₂Se₃ and β′- In₂Se₃ on strain and layer number, obtained by DFT calculations. (C) Polarized-light OM image at the polarizer azimuth angle φ = 70° presenting the typical gradient morphology of β′-In₂Se₃. (D) HAADF image of the edge of the β′-In₂Se₃. (E) The SAED patterns corresponding to the 2L-5L In₂Se₃, respectively. The superspots (red circles) of In₂Se₃ disappear for layer number less than four. (F) Atomic HAADF image and corresponding image simulation results of few-layer β′-In₂Se₃. (G) HAADF image and corresponding image simulation results of 1L α-In₂Se₃. (H) Intensity line profile corresponding to the line in (G). Atomic differential phase contrast image of (I) β′-In₂Se₃ phase and (J) α-In₂Se₃, respectively. The yellow arrows indicate the intrinsics polarization directions in AFE β′-In₂Se₃. Scale bars, 50 μm (C), 2 μm (D), 2 1/nm in (E), 1 nm (F and G), and 2 nm (I and J), respectively.

RESULTS

Thickness dependence of phases in 2D In₂Se₃

We synthesized the β′-In₂Se₃ single crystals using the CVD method (see Materials and Methods and fig. S1). The crystal structure of the β′-In₂Se₃ is shown in Fig. 1A. Because of the spontaneous polarization of the center Se atoms, few-layer β′-In₂Se₃ was reported with AFE structures (26). We examine the phase stability as a function of layer number and the biaxial strain using DFT calculations (see Materials and Methods; Fig. 1B). The result shows that α and β′ phases indeed have very close energies, with the ground state of α phase slightly lower than that of β′ phase, and β′ phase overwhelms α phase under tensile strain, irrespective of thickness. However, we experimentally observed different favorable phases changing with thickness. The typical optical microscope (OM) image of β′-In₂Se₃ with a regular triangle shape and bright-field TEM (BF-TEM) image with apparent stripe-like domain structures can be seen in fig. S2 (A and B). The selected area electron diffraction (SAED) patterns with superspots corresponding to the periodic AFE supercell and the Raman spectrum presented in fig. S2 (B and C) also show the characteristics of β′ phase.

The wedge-shape edges of synthesized β′-In₂Se₃ flakes are particularly interesting. The polarized-light OM image (Fig. 1C) shows domain structures in thicker β′-In₂Se₃. As thickness decreases, the contrast of domains gradually vanishes. To attain better contrast, scanning TEM (STEM) with the high-angle annual dark-field (HAADF) technique is used to identify the number of layers at the edge of the β′-In₂Se₃, shown in Fig. 1D and fig. S3 (A and B), and the corresponding SAED patterns shown in Fig. 1E. The STEM-HAADF intensity ratio is linearly correlated with the number of layers at the edges (see Materials and Methods).

We find that when the number of layers is equal to or more than four, In₂Se₃ remains β′ phase with superspots in SAED (marked by red circles). On the contrary, when the number of layers is less than four, the superspots in the SAED pattern disappear, showing the phase transition from β′-In₂Se₃ to α-In₂Se₃ (Fig. 1E and fig. S3, C to E). Atomic-resolution STEM-HAADF images of 5L and 1L In₂Se₃ are shown in Fig. 1 (F and G, respectively), reconciling the phase identification results above. The results of atomic force microscope (AFM) and corresponding Raman spectra also prove the thickness dependence of phases in In₂Se₃ (fig. S4) and during the transfer process from mica to polymethyl methacrylate (PMMA) and TEM grid, no phase transition occurs (fig. S5). Apparent atomic structures with bright and dark contrast are observed in 5L In₂Se₃, which is believed to be β′-In₂Se₃ (Fig. 1F). 1L In₂Se₃ area is verified in α phase, which is shown by the projected atomic positions of In + Se, In, and Se + Se (Fig. 1G), and the relevant intensity line profile is presented in Fig. 1H. The atomic structure and the corresponding STEM-HAADF image simulation (see Materials and Methods) results of 1L β′-In₂Se₃ and β-In₂Se₃ are shown in fig. S6 with projected atomic positions of In + Se, In + Se, and Se, which is distinct from our experimental images of 1L area. The STEM–differential phase contrast (DPC) images show the electric polarization fields (see Materials and Methods). The DPC image with periodic contrast in Fig. 1I indicates strong in-plane electric polarization field in AFE β′-In₂Se₃; the net in-plane polarization observed in β′-In₂Se₃ may imply that it has ferrielectric property resulted from the competition between FE and AFE orders (35). The net polarization direction is indexed by the yellow arrow. Compared with the β′-In₂Se₃, because of the weaker in-plane electric polarization field, the DPC result of α-In₂Se₃ presents darker contrast in Fig. 1J.

These results indicate that the AFE β′-In₂Se₃ is thickness dependent and likely becomes less stable than α-In₂Se₃ in ultrathin 2D layers (<4L). This evolution of stability with thickness is probably caused by the strain. For the thick sample, there should be still residual tensile strain in the sample after cooling from high temperature, which maintains the thick samples in β′ phase, while for thinner samples, the strain is liable to relaxation and trigger the β′-α phase transition during the CVD cooling/transfer process. Because of the smaller bending rigidity of thin (<4 layer) samples, they are prone to out-of-plane curling, buckling and wrinkling, and edge delamination (36), which can lead to local delamination from the substrates (pristine growth substrate, PMMA substrate during transfer, or Si, TEM grid, and others after transfer); as a result, we can only observe the most stable nonstrained α phase in 2D In₂Se₃. In contrast, the thick layers are more rigid with notably larger bending rigidity, so these thicker (>4 layer) 2D In₂Se₃ samples are not easy to delaminate from substrates, and they could maintain the original tensile strain state and maintain the β′ phase. The TEM-measured in-plane lattice parameters of monolayer α phase and β′ phase can also justify the residual tensile strain in β′ phase (fig. S7). Detailed strain effect on the phase transition of 2D In₂Se₃ is unveiled by in situ TEM and discussed in the next section.

Strain-induced reversible phase transition in 2D In₂Se₃

Implied by our DFT results (Fig. 1B), strain can also effectively modulate the phase transition in 2D In₂Se₃. As shown in Fig. 2A, we use in situ TEM techniques to load/unload the mechanical strain on our 2D samples. By using a piezo-driven nanomanipulator (see Materials and Methods), the nano-sized tungsten (W) tip applies the stress with subnanometer displacement precision. Dark-field TEM (DF-TEM) is carried out to characterize the domain structures in β′-In₂Se₃. Before in situ manipulation, the β′-In₂Se₃ shows typical nanodomain structures and superspots in the SAED pattern corresponding to the AFE phase (Fig. 2B). The W tip is then compressed downward (along z direction) approximately along the viewing direction of TEM. During compression, the β′-In₂Se₃ remains unchanged with intact domain structures shown in Fig. 2 (C and D). After compression by ca. 5.55 nm, the W tip is pulled back in reverse direction. As shown in Fig. 2 (E to H), the transition from β′-In₂Se₃ to α-In₂Se₃ occurs in this reverse process. In this process, the phase transition front (α/β′ interface) was determined by the contrast of nanodomains in DF-TEM. More details of the phase transition process are recorded in fig. S8 and movie S1. Comparing the TEM morphology before and after in situ experiment (figs. S9 to S12), the originally flat sample morphology apparently turns wrinkled and rippled. The corresponding SAED patterns in Fig. 2H and the postmortem Raman spectrum on the same position of the manipulated TEM sample (fig. S12C) confirm the α phase formation after an in situ compression-relaxation process.

Fig. 2. In situ βʹ-In₂Se₃ to α-In₂Se₃ phase transition.

(A) Schematic illustration of the in situ TEM setup. (B) Typical DF-TEM image of β′-In₂Se₃ and corresponding SAED pattern at the moment when the W tip contacts the sample. The diffraction spot selected by objective aperture for dark field was indicated by the yellow circle at the right top of (B). (C to G) Sequential TEM image series during the in situ compression and relaxation by the W tip. Initially, the sample was entirely β′-In₂Se₃ with obvious stripe-like domain structures in (B) to (D). After compression, when the W tip is reversely pulled back, the β′-In₂Se₃ starts to transform into α-In₂Se₃ and the domain structures gradually disappeared in (E) to (G). (H) DF-TEM image and corresponding SAED pattern of the resulted α-In₂Se₃ after in situ loading-unloading. Scale bars, 1 μm. (I) Schematic graphs of the in situ TEM compression-relaxation process of β′-In₂Se₃–to–α-In₂Se₃ phase transition. (J to L) The DFT calculation results of the strain-dependent energy evolution for different In₂Se₃ phases. Scale bars, 1 μm (B); (D) to (H) have the same scale bar as (B). Scale bars of SAED pattern in (B) and (H) are both 2 1/nm.

In addition, the in situ BF-TEM experiments for smaller and larger areas in 2D In₂Se₃ clearly manifest the morphology transformation during the compression-relaxation process (figs. S9 to S11 and movies S2 to S4). Before phase transition, the β′-In₂Se₃ on substrate (a-carbon in TEM grid) is smooth without noticeable contrast variation (figs. S9A and S11A), implying the ultraflat condition and firm attachment with the substrate. However, during the phase transition from β′-In₂Se₃ to α-In₂Se₃ (pull-back of W tip), obvious wrinkles and ripples with additional TEM contrast occur in α-In₂Se₃ (figs. S9, D to F, and S11, B to F). The roughened, rippled, or wrinkled morphologies in the 2D In₂Se₃ after such mechanical loading-unloading process are further verified by the equal inclination fringe analysis (figs. S13 and S14).

Hence, a schematic graph of the above in situ TEM phase modulation process is shown in Fig. 2I. Originally, β′-In₂Se₃ is stretched and fixed by the underlying substrate—amorphous carbon (a-carbon) and suffers biaxial tensile strain, which is normally caused by the cooling stress during CVD growth (36). The strain tends to be maintained during the PMMA transfer process for TEM sample preparation (see Materials and Methods and fig. S5). Upon the in situ TEM manipulation, when the W tip moves away from the β′-In₂Se₃, the delamination between β′-In₂Se₃ and the substrate (a-carbon) occurs with strain relaxation in β′-In₂Se₃. This mechanical delamination is partially enhanced by the differences in flexural modulus and elastic modulus of β′-In₂Se₃ and a-carbon substrate. In this way, the tensile strain originally restored in β′-In₂Se₃ applied by the substrate is released, which results in the phase transition from β′-In₂Se₃ to α-In₂Se₃. The lattice parameter of original β′-In₂Se₃ is larger than the relaxed α-In₂Se₃ (fig. S15), which further proves the strain relaxation in the compression-relaxation phase transition process. After the strain relaxation, the β′-In₂Se₃ film (1185.7 μm²) almost entirely transforms into α-In₂Se₃ (fig. S12). We also transfer the β′-In₂Se₃ film from mica to rough Cu substrate (fig. S16). Compared with transferred 2D film from mica to TEM grid, rough Cu substrate cannot attach with 2D In₂Se₃ well and cannot maintain the strain therein. The formation of ripples in 2D samples on rough Cu surface (fig. S16C) also indicates the delamination and strain relaxation, which corroborates with the in situ TEM results that after phase transition from β′-In₂Se₃ to α phase, many wrinkles are formed in the film because of the delamination process.

To further rationalize the strain effect on the phase stability in 2D In₂Se₃, we performed DFT calculations on β′-In₂Se₃ and α-In₂Se₃ under biaxial strain. As shown in Fig. 2 (J to L), the relationship between lattice constant (lattice strain) and energy for α-In₂Se₃ and β′-In₂Se₃ can be identified. The calculated in-equilibrium lattice constants (a) for α-In₂Se₃ and β′-In₂Se₃ are very close, 4.181 and 4.177 Å for 1L α-In₂Se₃ and β′-In₂Se₃, respectively. Without the external strain, the energy of α-In₂Se₃ is slightly lower than β′-In₂Se₃ regardless of the thickness. With the increasing of strain, the energy difference between β′-In₂Se₃ and α-In₂Se₃ is reduced, with interceptions at ca. 5 to 8% strain. According to thermodynamics and our DFT results, the α-β′ phase transition occurs and the mixed-phase state exists with the biaxial strain ranging from 5.55% (monolayer), 6.37% (four layer), to 7.11% (six layer), determined by the tangential line [black lines in Fig. 2 (J to L)] of the two equation-of-state curves (see Materials and Methods). Therefore, our experiments and DFT results confirm the critical role of the tensile strain on the phase control in 2D In₂Se₃. In addition, Raman spectroscopy (fig. S17) was used to determine the strain level during the transfer process, similar as MoS₂ (37, 38). Compared with the significant shift of A_1g¹ peak of β′-In₂Se₃ on the TEM grid hole where a certain degree of strain has been released, little shift of A_1g¹ peak of β′-In₂Se₃ on mica, PMMA, and SiO₂ substrates proved that the strain can be maintained during the PMMA transfer process.

Apart from the tensile strain relaxation that induces phase transition from β′-In₂Se₃ to α-In₂Se₃, α-In₂Se₃ is expected to transform back into β′-In₂Se₃ when tensile strain is applied. The scheme for this in situ TEM tensile experiment is shown in Fig. 3A. The 2D α-In₂Se₃ sample (on TEM grid) obtained via the above strain relaxation approach is firmly coupled with a Cu tablet, and then the entire TEM grid with a 2D sample on it can be stretched with the elongated Cu tablets mounted on an in situ TEM tensile holder (see Materials and Methods). As shown in Fig. 3 (B to I), BF-TEM is used to record the in situ tensile process. Before the start, α-In₂Se₃ is observed with many wrinkles. The SAED pattern without superspots in the top right of Fig. 3B confirms the absence of β′ phase. During the tensile process, with the increase in tensile distance of Cu tablet labeled on the top left of Fig. 3 (B to H), no phase changes are observed in α-In₂Se₃ at first. Until the tensile distance increases from 310 to 323 μm, numerous β′-In₂Se₃ domains suddenly appear and superspots emerge in the SAED pattern, in agreement with the phase transition from α-In₂Se₃ to β′-In₂Se₃ after the tensile strain reached the critical point. The recorded in situ TEM process is shown in movie S5. During the tensile process, some superspots appear in the SAED patterns of the α-In₂Se₃, which is induced by appearance of ordered structure during in situ tension experiment (fig. S18). It is worth noting that the β′-In₂Se₃ in Fig. 3H has less wrinkles or ripples than the initial α-In₂Se₃. Although the tensile distance is completely released to zero (back to starting point), the 2D In₂Se₃ still maintains the β′ phase (Fig. 3I) because of the irrecoverable plastic deformation in Cu chips and TEM grid. The scheme of the above transformation process from α-In₂Se₃ to β′-In₂Se₃ is presented in Fig. 3J. Meanwhile, according to the strain relaxation and in situ tension, a complete reversible process (β′-In₂Se₃ → α-In₂Se₃ → β′-In₂Se₃) has also been achieved on the same 2D flake sample (fig. S19).

Fig. 3. In situ α-In₂Se₃–to–βʹ-In₂Se₃ phase transition.

(A) Schematic illustration of the setup of the in situ TEM tensile experiment. (B to I) Sequential BF-TEM images during the tension and relaxation process. The uniaxial tensile direction is indicated by the yellow arrow in (B). Initially, the sample is entirely α-In₂Se₃ with wrinkles/ripples in (B) to (G). When the tensile distance reaches 323 μm, the α-In₂Se₃ transforms into β′-In₂Se₃ with striped domain structures (pink arrows) in (H). (I) TEM image and corresponding SAED pattern of the β′-In₂Se₃ after the entire in situ loading-unloading. (J) Scheme of the tensile strain induced phase transition from α-In₂Se₃ to β′-In₂Se₃. (K and L) The high-resolution HAADF images and corresponding simulation images of α phase and β′ phase during in situ process above. (M and N) The high-resolution HAADF image of the α/β′ interface and the corresponding GPA results. Scale bars, 1 μm (B to I) and 1 nm (K to M). Scale bars of SAED patterns in (B) to (I) are same as the scale bar of 2 1/nm in (B).

In addition, the atomic-resolution STEM-HAADF images of the α-In₂Se₃ and β′-In₂Se₃ during phase transition (Fig. 3, K and L) are matched with the multislice STEM image simulation results shown as insets of Fig. 3 (K and L). The atomic-resolution HAADF image and the corresponding strain distribution in different phases acquired at the α/β′ interface by geometric phase analysis (GPA) method (see Materials and Methods) are presented in Fig. 3 (M and N), respectively. Considerable relative tensile strain can be observed on the β′-In₂Se₃ side, and relative compressive strain (still in tensile range with respect to equilibrium state) on the α-In₂Se₃ side, in line with the DFT results. In this way, via strain manipulations, reversible phase transition between AFE β′-In₂Se₃ and out-of-plane FE α-In₂Se₃ can be readily achieved. Meanwhile, guided by the unraveled strain relaxation concept and phase transition application on other 2D materials (11, 14), FE field-effect transistors (FE-FETs) realized by phase transition are designed and FE memory performance of β′-In₂Se₃ and α-In₂Se₃ FE-FET are tested (figs. S20 and S21 and Materials and Methods), which shows promising performance.

Phase modulation in 2D In₂Se₃ enabled by in situ electrical TEM

Electrical stimuli influence materials through the electric field and the thermal effect (joule heating) (39). Here, we explore the phase transitions in 2D In₂Se₃ triggered by electrical stimuli using in situ TEM. We find that α-In₂Se₃ can transform into β′-In₂Se₃ and further γ-In₂Se₃, by the applied bias/current. The scheme of our in situ electrical TEM setup is shown in Fig. 4A. The bias/current is applied/measured by Keithley 2400 connected to the piezo nanomanipulator described above (see Materials and Methods). Our results show that through intensive electrical current (see Materials and Methods), the heat generated triggers the phase transition in 2D α-In₂Se₃. As shown in Fig. 4B, when relatively low current is applied, the phase transition from α-In₂Se₃ to β′-In₂Se₃ occurs. While the electrical current is relatively higher, the direct α-In₂Se₃–to–γ-In₂Se₃ transition occurs. In literature, the transition temperatures for these two transitions are 200°C (30, 40) and 520°C (41), respectively.

Fig. 4. In situ electrically stimulated α-In₂Se₃ to β’-In₂Se₃, and γ-In₂Se₃ phase transitions.

(A) Schematic illustration of the in situ electrical TEM setup. (B) Schematic graphs of the α-In₂Se₃ to β′-In₂Se₃ and γ-In₂Se₃ phase transitions under electrical stimuli. (C to E) Sequential TEM images when applying low current; α-In₂Se₃ transformed to β′-In₂Se₃ affected by electrical field and joule heat. (F) Temperature distribution after applying low current. (G to I) Sequential TEM images when applying high current; α-In₂Se₃ transforms into γ-In₂Se₃ (inner) and β′-In₂Se₃ (outer). (J) Temperature distribution after applying high current. Scale bars, 1 μm (C to E and G to I). Scale bars of SAED patterns in (C), (E), (G), and (I) are same as the scale bar 2 1/nm in (C).

The in situ electrical TEM processes are detailed in Fig. 4 (C to J). Figure 4 (C to E) shows the transition from α-In₂Se₃ to β′-In₂Se₃ at a relatively low current. Before the start, the SAED pattern in Fig. 4C confirms the α phase. After applying current, superspots appear in the SAED pattern (Fig. 4E), indicating the transition to β′-In₂Se₃ (movie S6). The corresponding I-V cycle is shown in fig. S22. The phase transition current for this case is ca. 5 × 10⁻⁵ A. Figure 4F shows the calculated temperature distribution (see Materials and Methods) for the current of 5 × 10⁻⁵ A. On the basis of the reported critical transition temperature (200°C) from α-In₂Se₃ to β′-In₂Se₃, we can estimate the radius of new β′-In₂Se₃ area by joule heating mechanism. The radius of the new phase area is calculated as 5.77 μm (Fig. 4F), perfectly matching with our experimental results of 5.6 μm (fig. S22 and table S1). Next, when we apply higher current (8 × 10⁻⁵ A) on the α phase (Fig. 4, G to I, and fig. S23), the temperature in the center of the contact area significantly increases. Correspondingly, the 2D In₂Se₃ transforms from α phase (Fig. 4G) to γ phase, as shown in Fig. 4I (movie S7), confirmed by the SAED patterns before and after in situ electrical stimuli. To better distinguish different phases, the relationship between the atomic structure and SAED patterns (both experiment and simulation) of α, β′, and γ phases are presented in fig. S24. In addition, to exclude the chemical changes induced by thermal energy generated during the above process, we also measure the element distribution before and after in situ TEM using energy-dispersive spectrum (EDS), which shows the unchanged atomic ratio 2:3 for In and Se (fig. S23B). The complete phase changes in the entire 2D In₂Se₃ film under high current (8 × 10⁻⁵ A) are also shown in fig. S23.

Polarization modulation in 2D In₂Se₃ via in situ electrical TEM

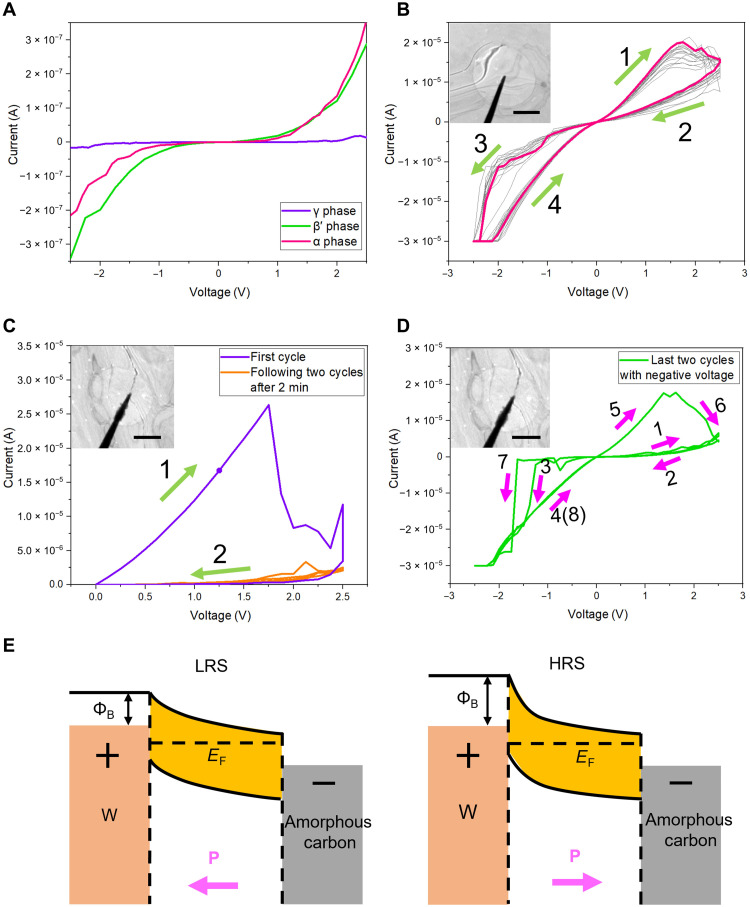
Under the direct effect of electric field, the FE polarization can be tuned in 2D In₂Se₃ as well. Different from the joule heating discussed in the previous section, here, we apply continuous and milder bias/current using the in situ electrical TEM technique. First, with point-like contact, the I-V curves at different phases of 2D In₂Se₃ can be measured (Fig. 5A). The results show that while all the contacts are governed by the Schottky barriers (42), α-In₂Se₃ and β′-In₂Se₃ have better conductivity compared with γ-In₂Se₃. Next, as we applied cycled bias on different phases, they show different characteristics. After several I-V cycles for electroforming (fig. S25, A and B), resistive hysteresis characteristics can be seen in α-In₂Se₃ (Fig. 5C); however, no resistive memory effect is observed in β′-In₂Se₃ and γ-In₂Se₃ (fig. S26, C and D).

Fig. 5. Electric polarization modulation and memoristive effects in 2D In₂Se₃.

(A) The I-V curve for the different 2D In₂Se₃ phases. (B) I-V cyclic curve for α-In₂Se₃. Green arrows indicate the switching directions. (C) Resistive switching characteristics of the α-In₂Se₃ at positive bias. After the first cycle, the resistive switching disappears for the following I-V cycles. (D) Resistive switching characteristics recover after applying negative bias on the α-In₂Se₃ after processes shown in (C). The top-left corner images of (B) to (D) are corresponding BF-TEM images of the contact made by W tip with 2D In₂Se₃. Scale bars, 500 nm. (E) Schematic band diagrams for the FE polarization modulation and effects on the Schottky barrier height. LRS, low-resistance state; HRS, high-resistance state.

Further experiments are carried out to understand such resistive memory mechanism in α-In₂Se₃. As shown in Fig. 5C, during the first I-V cycle in positive bias, the α-In₂Se₃ experiences a reset process at 1.75 V. However, when we run the second and third cycles at positive voltage after 2 min, the resistive memory effect disappears, meaning that the α-In₂Se₃ still maintains the reset situation. Such behavior confirms that the α-In₂Se₃ has the potential for nonvolatile memory applications (43, 44). Meanwhile, on the same α-In₂Se₃ sample, when we apply I-V cycles with negative bias, the set process is completed at −1.35 V in the first cycle, and in the following cycle, obvious resistive memory effect is recovered under positive bias (Fig. 5D).

The morphology of samples and structure changes during the above I-V cycle are shown in fig. S26 and movie S8. The morphology of α-In₂Se₃ does not have apparent change, and the corresponding SAED patterns before and after the I-V cycle all indicate that the 2D sample maintains α-In₂Se₃ structure, which suggests that the memristive behavior is not due to the phase transition. In fig. S27, the HAADF-STEM image does not show contrast of defects emerging in α-In₂Se₃ after 15 cycles. Therefore, the conductivity changes are most likely attributed to the FE polarization in 2D α-In₂Se₃, explainable by the shift of Schottky barrier height under positive and negative biases (Fig. 5E). When the polarization is in the direction (negative bias) of the external electrical field, depletion region is formed and lower barrier height with low-resistance state is rendered. With the increasing of positive bias, the intrinsic polarization of α-In₂Se₃ will switch to the opposite z direction. In this case, more electrons are accumulated at the W/α-In₂Se₃ interface and result in higher Schottky barrier height and high-resistance state. Thus, the polarization in α-In₂Se₃ manipulated by the external electric field can successfully control the current and conductance of the channel with nonvolatile memory effects.

DISCUSSION

In summary, we report the thickness, strain, and electrically controlled phase and polarization modulation in CVD-synthesized 2D In₂Se₃. There is a critical layer thickness above which the α phase tends to transform into β′ phase. According to our in situ TEM results, the strain-induced reversible phase transition from β′-In₂Se₃ to α-In₂Se₃ has been confirmed. In addition, the in situ electrical TEM reveals the joule heat–modulated phases of α-, β′-, and γ-In₂Se₃. Last, the reversible nonvolatile resistive switching is achieved in FE α-In₂Se₃. These results provide new valuable insights into the phase manipulations in 2D materials and can potentially stimulate new applications in nanoelectromechanical systems and memory devices for the 2D FE materials and their phase hybrids.

MATERIALS AND METHODS

Synthesis of 2D β′-In₂Se₃

2D β′-In₂Se₃ films were grown on mica substrates at 800° to 850°C for 10 to 15 min under a flow of 50–standard cubic centimeter per minute argon using In₂Se₃ powder as precursor by atmospheric-pressure CVD. The detailed CVD and cooling process is presented in fig. S1.

(S)TEM specimen preparation

By the PMMA-assisted technique, the CVD-grown In₂Se₃ was transferred onto a TEM grid. First, thin-layer PMMA was spin-coated on the as-grown mica substrate at 500 rpm for 10 s and then 3000 rpm for 60 s. After heating at 100°C for 5 min, another thin-layer PMMA was spin-coated again on the as-grown mica substrate at 500 rpm for 10s and then 1000 rpm for 30 s. With the PMMA, the In₂Se₃ detached from the substrate by immersing in deionized water at room temperature for 10 min. Next, the PMMA/In₂Se₃ layer was transferred onto a TEM grid and dried at 50°C. Last, acetone was used to wipe off the PMMA.

Determination of sample thickness

The ability of electron scattering is determined by the composition elements and thickness of the sample. When the composition elements for the materials are the same, the relationship between intensity I and object thickness t can be described as (45)

$$I=I_0(1-\text{exp}(-\mathrm{\mu }t))$$ (1)

where I₀ is the intensity of the beam as it enters the object and μ is defined as the attenuation coefficient and equals the inverse of the mean free path between scattering events. The equation can be simplified as follow by Taylor series

$$I=I_0(\mathrm{\mu }t-1/2(\mathrm{\mu }t{)}^2)$$ (2)

In addition, when the thickness is less than 10 nm, the relationship between intensity I and object thickness t is nearly linear (45).

In situ TEM

In situ observation of the phase transition of In₂Se₃ was performed with JEOL 2100F. The in situ compression-relaxation experiment and electrical measurements were carried out by a nanofactory in situ holder with a pizeo-controlled tungsten tip. The pizeo-controlled tungsten tip can provide accurate compression depth to contact different samples (maximum, ±14 μm; minimum step, 2 pm). The electrical measurements were done on the Keithley 2400, which is controlled by the LabVIEW program. The in situ tension experiment in transmission electron microscope was achieved by Gatan 654 single tilt straining holder. The quantifoil TEM grid with relaxed α-In₂Se₃ is stuck in the Cu tablet, which enable the simultaneous deformation between Cu tablet and α-In₂Se₃.

STEM characterization and EDS analysis

The atomic-scale HAADF-STEM images of different In₂Se₃ phases were obtained by the JEM-ARM200F TEM with the cold field emission gun and the Corrected Electron Optical Systems probe spherical aberration corrector and an operated accelerating voltage of 200 kV. The vacuum during the measurement was kept at 7.7 × 10⁻⁷ mbar, and the electron beam current was 13.3 μA. For image acquisition, the camera length on STEM was 120 mm. With a defocus of 5 nm, the acquisition time of HAADF images is 19 μs per pixel. Wiener filtering was applied on HAADF-STEM images for reduction of noises. Elemental results of different In₂Se₃ phase were obtained from JEOL 2100F with an energy-dispersive x-ray spectrometer operated at 200 kV. Atomic-resolution DPC-STEM imaging was performed with a convergence angle of 24.4 mrad and a four-quadrant annular detector after probe aberration corrected in the Thermal-Fisher Spectra 300 TEM. The spot size was 5 and the probe current was 30 pA. The dwell time was 16 μs for DPC-STEM acquisition with the collection angle of 12 to 45 mrad and the pixel size of 0.4967 Å.

HAADF-STEM simulation

The STEM simulation is accomplished in Dr. Probe (46) by a dynamic multislice method. The parameters are set as the same as experimental imaging condition. The simulation used the DFT calculation results of β′-In₂Se₃ and α-In₂Se₃ with the accuracy of 0.01 nm/pixel.

Strain analysis on TEM image

The GPA analysis (on high-resolution HAADF-STEM image) (47) was performed with the reflexes (in reciprocal space) perpendicular to the a and b directions as the two bases, respectively.

Phase stability analysis under strain

Taking the phase-lattice constant separation using a 1D problem as an example, which is similar as the free energy versus strain (48). For a two-phase system, there are two phase regions, L^α and L^β. Because the total extension of lattice is conserved, the overall extension of lattice constant can be described as

$$a^0=f^{\mathrm{\alpha }}{a}^{\mathrm{\alpha }}+f^{\mathrm{\beta }}{a}^{\mathrm{\beta }}$$ (3)

Here, the f^α and f^β are the fractions of α phase and β phase. Meanwhile, a^α and a^β are the extension of lattice parameter in α phase and β phase, respectively. According to the lever rule based on the Eq. 3, the fraction of two phases can be determined as follows

$$f^{\mathrm{\alpha }}=\frac{a^{\mathrm{\beta }}-a^0}{a^{\mathrm{\beta }}-a^{\mathrm{\alpha }}}$$ (4)

The Helmholtz free energy density of the two-phase system under isothermal-isobaric conditions can be described as

$$F^0=f^{\mathrm{\alpha }}{F}^{\mathrm{\alpha }}+(1-f^{\mathrm{\alpha }})F^{\mathrm{\beta }}$$ (5)

Here, the F^α and F^β are Helmholtz free energy density related with the a^α and a^β. Under the state of equilibrium, $\frac{ \mathrm{\partial }{F}^0}{\mathrm{\partial }{f}^{\mathrm{\alpha }}}=0$ and $\frac{ \mathrm{\partial }{F}^0}{\mathrm{\partial }{a}^{\mathrm{\alpha }}}=0$ and then we can deduce

$$\frac{\mathrm{\partial }{F}^{\mathrm{\alpha }}}{\mathrm{\partial }{a}^{\mathrm{\alpha }}}=\frac{\mathrm{\partial }{F}^{\mathrm{\beta }}}{\mathrm{\partial }{a}^{\mathrm{\beta }}}$$ (6)

$$\frac{F^{\mathrm{\beta }}-F^{\mathrm{\alpha }}}{a^{\mathrm{\beta }}-a^{\mathrm{\alpha }}}=\frac{\mathrm{\partial }{F}^{\mathrm{\beta }}}{\mathrm{\partial }{a}^{\mathrm{\beta }}}$$ (7)

Equations 6 and 7 show that the common tangent of the free energy–lattice constant curve determines the equilibrium free energy and extension of lattice parameter of mixed phases.

Transfer of α-In₂Se₃ films

After spin-coating PMMA and baking, the PMMA/α-In₂Se₃/Cu was immersed in 1 M ammonium persulfate solution for 5 hours to etch the Cu substrate, and then the PMMA/α-In₂Se₃ film was collected by SiO₂/Si substrate and baked at 50°C for 10 min. After removing the PMMA by acetone, the α-In₂Se₃ film was transferred to the SiO₂/Si substrate.

Device fabrication and measurement

After covering the In₂Se₃ films by metal hard mask, 40-nm Au was deposited to the films for contact electrodes (Denton Explorer E-beam Deposition System). The devices were tested by the semiconductor analyzer (Keithley 4200) in a probe station (Lake Shore).

Temperature field analysis

Here, we assume that the heat transfer is dominated by the In₂Se₃, because the thermal conductivity of a-carbon is 0.6, which is less than the thermal conductivity of 2D In₂Se₃ (12 to 18 W/mK), and the vacuum did not conduct heat in the TEM. In addition, steady-state heat transfer model was used to fit the temperature field induced by current. The joule heat generated by current per second can be demonstrated as follows

$$Q=I^{2}R$$ (8)

According to the steady-state heat transfer model, the 2D In₂Se₃ can be seen as a hollow cylinder, the inside diameter r₁ can be seen as the diameter of the W tip, and the outside diameter r₂ can be seen as the distance between the W tip and the Cu screen. In this way, according to the Fourier law, we can get the relationship between temperature field and rate of heat flow as follows

$$\mathrm{\Phi }=\frac{2\mathrm{\pi }\mathrm{\lambda }l(t_{\mathrm{r}1}-t_{\mathrm{r}2})}{\text{ln}\left(\frac{{\mathrm{r}}_2}{{\mathrm{r}}_1}\right)}$$ (9)

Here, Φ is the rate of heat flow, which is equal to Q, and the t_r1 and t_r2 are the temperature at the W tip and the Cu screen, respectively. λ is the thermal conductivity of the 2D In₂Se₃, and l is the thickness of the 2D In₂Se₃. Because the W tip is not at the center of the Cu screen, we can measure the shortest distance r_S and the longest distance r_L between the W tip and the Cu screen and then Eq. 9 can be modified as

$$\mathrm{\Phi }=\frac{2\mathrm{\pi }\mathrm{\lambda }\mathrm{l}(t_{\mathrm{r}1}-t_{\mathrm{r}2})}{\frac{\text{ln}\left(\frac{r_{\mathrm{s}}}{r_1}\right)+\text{ln}\left(\frac{r_{\mathrm{L}}}{r_1}\right)}{2}}$$ (10)

The average distance r_a can be defined as the $\text{ln}\left(\frac{r_{\mathrm{a}}}{r_1}\right)$= $\frac{\text{ln}\left(\frac{r_{\mathrm{s}}}{r_1}\right)+\text{ln}\left(\frac{r_{\mathrm{L}}}{r_1}\right)}{2}$, and we can get the result that $r_{\mathrm{a}}=\sqrt{r_{\mathrm{s}}{r}_{\mathrm{L}}}$. In this way, we hypothesis the temperature t_r2 of Cu screen is room temperature 25°C. Then, we can calculate the temperature t_r1 at the contact area of the W tip and 2D In₂Se₃. Next, we can get the temperature field of the whole 2D In₂Se₃ by following equation

$$t(r)=t_{\mathrm{r}1}-\frac{({\mathrm{t}}_{\mathrm{r}1}-{\mathrm{t}}_{\mathrm{r}2})\text{ln}\left(\frac{r}{r_1}\right)}{\text{ln}\left(\frac{\sqrt{r_{\mathrm{s}}{r}_{\mathrm{L}}}}{r_1}\right)}$$ (11)

t(r) is temperature function ranges with the distance r between certain area and W tip. All the parameters have been measured as shown in table S1.

SAED pattern simulation

The SAED pattern simulation was achieved by JEMS by the Bloch wave method (49). The accelerating voltage is 200 kV, and the thickness of the sample is set as 10 nm. Other parameters are same as the JEOL 2100F TEM. The crystal structure and lattice parameters are same as our DFT results.

DFT calculation

DFT calculations were performed to achieve optimized geometrical and strain-dependent energy change using the Vienna Ab Initio Simulation Package code (VASP.5.4.4.18) (50, 51) with the projector augmented wave (52) basis and the vdW-DF exchange-correlation functional method (53, 54). The kinetic energy cutoff was set to 350 eV. The first Brillouin zone was sampled by Γ-centered 9 × 3 × 1 k-point grids for the structural relaxation. Total energy and the force on each atom were converged to less than 10⁻⁵ eV and 0.02 eV/Å, respectively. The vacuum space of more than 15 Å along the z direction was used to minimize possible periodic interactions.

Supplementary Materials

This PDF file includes:

Figs. S1 to S27

Table S1

References

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S8