Abstract

The excitation energy transfer (ET) pathway and mechanism from an organic antenna to a lanthanide ion has been the subject of discussion for many decades. In the case of europium (Eu3+), it has been suggested that the transfer originates from the ligand singlet state or a triplet state. Taking the lanthanide complex Eu(TTA)3(H2O)2 as an example, we have investigated the spectra and luminescence kinetics, mainly at room temperature and 77 K, to acquire the necessary experimental data. We put forward an experimental and theoretical approach to measure the energy transfer rates from the antenna to different Eu3+ levels using the Dexter formulation. We find that transfer from the ligand singlet state to Eu3+ may account for the ET pathway, by combined electric dipole–electric dipole (ED–ED) and ED-electric quadrupole (EQ) mechanisms. The contributions from the triplet state by these mechanisms are very small. An independent systems rate equation approach can effectively model the experimental kinetics results. The model utilizes the cooperative processes that take place on the metal ion and ligand and considers S0, S1, and T1 ligand states in addition to 7F0,1, 5D0, 5D1, and 5DJ (=5L6, 5D3, 5D2 combined) Eu3+ states. The triplet exchange ET rate is estimated to be of the order 107 s–1. The observation of a nanosecond risetime for the Eu3+ 5D1 level does not enable the assignment of the ET route or the mechanism. Furthermore, the 5D1 risetime may be contributed by several processes. Observation of its temperature dependence and also that of the ground-state population can supply useful information concerning the mechanism because the change in metal-ion internal conversion rate has a greater effect than changes in singlet or triplet nonradiative rates. A critical comparison is included for the model of Malta employed in the online software LUMPAC and JOYSpectra. The theoretical treatment of the exchange mechanism and its contribution are now being considered.
Introduction
Lanthanide ions are versatile lighting and display elements, but their performance relies upon an efficient antenna because their absorption is very weak. Hence, there have been many thousands of papers describing the quantum efficiency and brightness of their complexes with organic ligands, particularly for europium, Eu3+. From experiment, some studies have proposed that the singlet state S1 (or a charge transfer (CT) state) is responsible for the transfer of energy from the coordinated ligand to the Eu3+ energy levels,1−5 whereas the majority of reports consider that energy transfer (ET) occurs from the ligand triplet state, T16−8 (Figure 1a). The understanding of the major ET pathway and mechanism is particularly important for the development and optimization of photovoltaic and optoelectronic devices, such as in lighting and displays, light-emitting diodes (LEDs), biomarkers, sensors, fluoroimmunoassays, and noncontact thermometers.9−13
Figure 1.
(a) Selected energy levels of the ligand-Eu3+ system. (b) Schematic structure of the complex. (c) X-ray structure of triclinic Isomer I of Eu(TTA)3(OH2)2 showing the disorder of the thienyl group in one of the coordinated TTA ligands14 (black bonds) superimposed upon Isomer II, the monoclinic structure15 (gray bonds). (d) Infrared spectra of Ln(TTA)3(OH2)2 complexes. (e) Calculated ultraviolet absorption spectra using time-dependent density functional theory (TD-DFT) for Eu(TTA)3(OH2)2 in the gas phase (black) and in toluene solution (red). The MWB52-PBE0/D3BJ/def2-TZVP level of theory was employed, and the CPCM model was employed for the solution spectrum. The CASSCF-NEVPT2 calculated spectrum using a (6,6) active space is shown in blue. (f) DFT frontier orbitals of Eu(TTA)3(OH2)2 in toluene solution.
Naturally, the Eu3+ population mechanism can depend upon many factors including the type of ligand system. However, confirmatory evidence from experiment should show that the Eu3+ acceptor luminescence risetime is equal to the donor decay time. Moreover, even the confirmation of the energy transfer route may not be sufficient to elucidate the relevant mechanism.6
Hence, attempts to unravel the population channel and its mechanism have turned to theory. However, to date, there has only been a comprehensive quantitative description given by Malta and co-workers12,16−18 for the transfer of energy from the antenna to the Eu3+ metal ion. The model of Malta, using the tensor operator techniques of Kushida,19 has been employed in many publications and has sometimes concluded that singlet ET occurs to Eu3+, and in other cases, triplet ET occurs. The earlier publications evidently overestimated the contributions from exchange ET. The model is available for use in free and widely used computation software programs called LUMPAC20 and JOYSpectra.21
The key question which has been targeted in many publications is: does the antenna ET originate from a singlet or a triplet channel? Naturally, both can contribute to varying extents. We present an alternative strategy for attacking this question which utilizes experimental data in conjunction with theory. The compound Eu(TTA)3(H2O)2 (TTA = thenoyltrifluoroacetonate) (Figure 1b) has been chosen for the demonstration of the results because it has been widely studied and applied,8,22−28 and it has been used for illustration in the software JOYSpectra.21 The temporal variation of the populations of ligand and metal states has been reproduced by a new rate equation model.
Methods
Materials
EuCl3·6H2O and LaCl3·7H2O were purchased from Sigma-Aldrich (≥99.99% trace-metal basis) and used without further purification. All organic chemicals were purchased from TCI or Energy Chemical with 98% purity and used without further purification.
Synthesis
Ln(TTA)3(H2O)2 were obtained according to a procedure following the literature method.24 Briefly, for Ln = Eu, HTTA (0.67 g, 3 mmol) was dissolved in 15 mL of ethanol in a 150 mL flask, with stirring at room temperature. Then, the pH of the solution was adjusted to 6–7 by the addition of NaOH solution (1.0 M). After that, 1 mmol of EuCl3·6H2O (0.37 g, 1 mmol) solution in 5.0 mL of deionized water was added to the above mixture at 60 °C. Then, deionized water (100 mL) was added to the above mixture with vigorous stirring for 2 h at 60 °C to ensure complete precipitation. After cooling to room temperature, the precipitate was filtered, washed repeatedly with water, and dried overnight under vacuum at room temperature to afford Eu(TTA)3(H2O)2 as a light yellow solid (0.68 g, 80%). Ln(TTA)3(H2O)2 (Ln = Gd, La) were prepared analogously. The compound easily decomposes in a moist atmosphere. The results of thermogravimetric analysis are shown in Figure S1.
Instruments
Excitation and emission spectra and luminescence decay curves were obtained by a Fluorolog-3 spectrometer from Horiba with a 450 W Xenon lamp, Horiba Nano, and Spectra LEDs as excitation sources. Spectra were recorded at 77 K with the samples in NMR tubes in a home-built liquid nitrogen setup made of glass. Experiments at the sensor reading of 10 K (i.e., the nominal 10 K temperature) were performed using an Optical Cryostat-CS202I-DMX-1SS from Advanced Research Systems Instruments, Inc. Emission spectra with higher resolution were also measured using an iHR 550 spectrometer with a system consisting of a Nd:YAG pump laser, a third-order harmonic generator (THG at 355 nm, 120 mJ), and an optical parameter oscillator (OPO, Spectra-Physics VersaScan, and UVScan) with a pulse duration of 8 ns and repetition frequency of 10 Hz. Absorption spectra were recorded at room temperature for solutions in quartz cuvettes using a PerkinElmer LAMBDA 1050+ UV/VIS/NIR double-beam spectrophotometer. A qX3/Horiba4 variable-temperature cell was employed to investigate the temperature dependence of emission between 280 and 323 K. A 10 mm pathlength cuvette was used for all room-temperature measurements. Fourier transform infrared (FT-IR) spectra were recorded using a PerkinElmer FT-IR Spectrum Two equipped with LiTaO3 detector.
Computation of Molecular Structure and State Energies. Rate Equations
Calculations were performed using Orca version 4.2.129,30 and accessories, together with the use of Avogadro31,32 and Gabedit.33 In these density functional theory (DFT) calculations, the PBE034,35 functional was employed with the def2-TZVP basis set,36 with the Stuttgart in-core effective core potential and basis set for Eu3+.37,38 In all optimizations, the Grimme dispersion correction D3BJ was used.39,40 The calculation for Eu(TTA)3(H2O)2 in toluene solvent used the Conductor-like Polarizable Continuum Model (CPCM).41 The optimized structures were checked to represent true minima by calculation confirming the absence of imaginary frequencies. The simulated absorption spectra employed a bandwidth of 2000 cm–1. The time-dependent DFT calculation employed 30 roots. Molecular orbital figures used the isosurface values of 0.05 e/a03 in all cases.
CASSCF-NEVPT2 calculations42−44 were also performed using ORCA 4.2.1. for 10 roots, following a second-order Møller–Plesset theory calculation with the optimized structure from the above DFT. The basis set 6-31+G(d)45 was used for all atoms except Eu, with the auxiliary basis: def2-TZVP/C.46
Multiwfn v3.7.47 was used to determine the molecular orbital coefficients at atomic positions. Distances from Eu to the relevant atoms were measured in Diamond48 and Avogadro.31,32
The wavefunction for 7F0 (or 5D0, for example) comprises several other SLJ multiplets in the intermediate coupling scheme. For example, for Eu3+ in Lu2O3, the wavefunction of 7F0 due to J-mixing is49
where the two numbers after the term represent J and MJ values. Hence, there is about a 5% contribution to the 7F0 wavefunction from 7F2 and this has been recognized in the reduced matrix elements given by Kasprzycka et al.50 Ideally, this contribution should be included in calculations, but for simplicity, we restrict our calculations to mainly order-of-magnitude results.
Maple 202151 was employed for computations involving the rate equation model.
Theoretical Background
The oscillator strength Pif of a transition between initial (i) and final (f) states of a system is measured experimentally from an emission spectrum if the low-temperature lifetime τ is approximated as the radiative lifetime τR, as52,53
| 1a |
or
| 1b |
where the virtual cavity model correction
for the macroscopic and local electric field has been inserted in
(eq 1b) for an electric
dipole (ED)-allowed transition 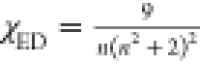 or χMD = n3 for a magnetic
dipole (MD)-allowed transition; ε0 (F m–1) is the vacuum permittivity, ν (s–1) is the transition frequency, c is the speed of
light (m s–1), m is the electron
mass (kg), λ is the emission wavelength
(in nm), n is the refractive index, and τR (s) = 1/A is the radiative lifetime
(A is the Einstein coefficient of spontaneous emission,
s–1).
or χMD = n3 for a magnetic
dipole (MD)-allowed transition; ε0 (F m–1) is the vacuum permittivity, ν (s–1) is the transition frequency, c is the speed of
light (m s–1), m is the electron
mass (kg), λ is the emission wavelength
(in nm), n is the refractive index, and τR (s) = 1/A is the radiative lifetime
(A is the Einstein coefficient of spontaneous emission,
s–1).
Alternatively, the oscillator strength can be approximately measured from the absorption spectrum: from the linear absorption coefficient α (m–1) or the absorption cross section σ (m2), where N (m–3) is the number of absorbing centers per unit volume, and i and f are the initial and final levels in the transition
| 2 |
| 3 |
Here, h is Planck’s constant (J s) and E = hν. Hence, in terms of ν̅ (cm–1)
| 4 |
or in terms of molar absorption coefficient, ε (mol–1 cm–1 dm3)
| 5 |
where
| 6 |
with l being the pathlength (cm), c the concentration (mol dm–3), and P0 and P the incident and transmitted power through the sample, respectively. The use of eq 5 pertains to the population of the initial state, which for 7F0 is rather less than 1.
The oscillator strength for an ED-allowed transition can be calculated from the line strength (in C2 m2), Sif (ED) = ∑i,f|⟨φf|μe|φi⟩|2 of the transition, where μe is the ED moment operator
| 7 |
and gi is the degeneracy of the initial state (which is usually omitted or often placed in the numerator). Since our cases correspond to nondegenerate (7F0 and S1) initial states, we do not go into detail here. In eq 7, ν̅ is the peak maximum in cm–1. For example, from eq 7, if Pif (singlet) = 0.5 at 25 000 cm–1, then Sif equals 4.7329 × 10–58 C2 m2 or 4.2537 × 10–35 esu2 cm2. The inclusion of local field effects changes the answer in eq 7 by a factor of ∼3.
The oscillator strengths for the analogous transitions in absorption and emission are related by the state degeneracies
| 8 |
The energy transfer rate by the ED–ED mechanism between the donor (D) and acceptor (A) separated by distance R (see later) can be written
| 9a |
| 9b |
where the units are ν (s–1) (the average frequency of the transitions involved), R (m), and the overlap integral between the normalized emission and absorption spectra is in J–1.
Now we consider interaction comprising an ED transition of the antenna and an electric quadrupole (EQ) transition of the lanthanide ion. The equation given by Dexter for this interaction, neglecting local field effects, is54
 |
10 |
which shows an R–8 dependence. In terms of line strengths, this can be written as52
| 11a |
| 11b |
where the dipole line strength refers to the ligand and the quadrupole line strength to europium, respectively.
The line strength of an EQ transition (in C2 m4) from lower level i to upper level f is given by55
 |
12a |
where λ is in nm; or in terms of oscillator strength
| 12b |
where α is the fine structure constant, a0 is the Bohr radius, ⟨r2⟩ is the expectation value of the radial wavefunction for Eu3+, and λ is in nm.
The line strength of a ligand ED transition (in C2 m2) from an upper level S1 to a lower level S0 (both with spin S = 0) is given by56,57
| 13 |
with λ in nm. For a given transition, the ratio52,54
| 14 |
Values of AEQ′ = 1/(n5 × τA(EQ)) for the Eu3+ free ion have been tabulated by Dodson and Zia.55 Values of AEQ for the transitions 5D2 → 7F0 at 21 752 cm–1 (460 nm) and 5G2 → 7F0 at 26 423 cm–1 (378 nm) are largest for those under consideration herein, with magnitudes of 3.14 × 10–3 and 4.92 × 10–3 s–1, respectively.
The distance R in eqs 9a–11b does not represent the average donor ligand (O)-Eu acceptor distance, but rather it is the electronic barycenter of the donor state, and the coefficients (ci) of the donor singlet or triplet molecular orbital at each atom i can be calculated by the Hirshfeld method using Multiwfn 3.7.47 The value of R is then
| 15 |
where Ri is the distance from atom i to Eu. We employed the results from our TD-DFT calculation, in addition to a second-order Møller–Plesset (MP2) perturbation calculation, of the orbital compositions of the ligand singlet and triplet states. The calculated values of R, in Å, for the singlet state are TD-DFT 3.79, MP2 4.56; and for the triplet state are TD-DFT 3.96, MP2 4.45. The value given in most publications12 is 4.5, and we prefer to use this value for reference since it basically agrees with our MP2 calculation results.
Although the free ion selection rules forbid the ED mechanism for the transition (and others) 5D0 → 7F0, the transition is usually observed by this mechanism with an oscillator strength of ∼10–8 due to the crystal field selection rules incorporating the admixture of other states into the initial and terminal levels. It is therefore considered that the use of eqs 9a and 9b are justified since the Eu3+ site symmetry is C1 in the present case. The contribution of vibronic structure to the intensity of an electronic transition is of paramount importance for high-symmetry systems,58 but for Eu3+ ions in organometallic systems, most of the spectral intensity arises from pure electronic transitions. Hence, for this reason, in our largely order-of-magnitude calculations, and to avoid unnecessary complication, we do not consider vibronic intensity contributions to spectra. Additionally, we do not consider contributions from magnetic dipole transitions.
Results and Discussion
Structure, Frontier Orbitals, and Calculated Spectra of Eu(TTA)3(H2O)2
The crystal structure of Eu(TTA)3(H2O)2 was reported by White (monoclinic, P21/c, Z = 4)15 and subsequently, for two further isomers (triclinic, P1̅, Z = 2) by Vallet and co-workers.14 The structures are overlaid in Figure 1c, and the reader is referred to the detailed comparison given by Vallet et al. In each case, the site symmetry of the Eu3+ ion is C1 and the coordination number is 8, including two aqua ligands. The FT-IR spectra of the Ln(TTA)3(H2O)2 complexes are shown in Figure 1d. The FT-IR spectrum is a good identification method, and we have compared our spectra with those previously published and with DFT calculation in Table S1.24,25,59 We modeled the structure using the ORCA 4.2.1 program,29,30 either in the gas phase or in toluene (employing the CPCM),41 and the nearest-neighbor bond distances are listed in Table S2, in comparison with those from the crystal structures. The common statistic is the longer distance for Eu–Ow bonds.
Singlet Energy and Oscillator Strength
Our TD-DFT calculations in the gas phase or toluene solution indicate the ultraviolet peak maximum of Eu(TTA)3(H2O)2 at ∼295 nm, Figure 1e, with the frontier orbitals from the gas-phase calculation shown in Figure 1f. The CASSCF-NEVPT2 calculation using a (6,6) active space indicates a longer wavelength, 347 nm. We envisage that after ultraviolet excitation, rapid intersystem crossing occurs from the higher singlet states to the lowest one, which then can undergo intersystem crossing and/or direct ET to Eu3+. The transfer occurs from the S1–S0 zero phonon line (ZPL) energy, and its detailed identification and energy are discussed in the Supporting Information (SI), Section S3. In conclusion, for Eu(TTA)3(H2O)2, we take the zero phonon line energy of the lowest singlet state at 25 410 cm–1 (394 nm) and the oscillator strength from 0.005 up to a maximum value of 0.05. We only consider energy transfer to Eu3+ levels below this energy, which are above or coincident with the 5D0 luminescent state. Table S3 lists the Eu3+ SLJ multiplet energy levels of several Eu3+ systems and shows that in the present ET process, Eu3+ could be excited to the 5DJ (J = 0–3) and 5L6 levels, which lie below S1 in energy.
Triplet Energy and Oscillator Strength
Malta et al.22 noted that the phosphorescence emission band in Gd(TTA)3(H2O)2 is not observed in Eu(TTA)3(H2O)2 and concluded that the ET from the lowest triplet state of the TTA ligand to Eu3+ is efficient. Other scenarios could be that the triplet level is bypassed and/or energy transfer also occurs from the singlet state. We have measured the low-temperature solid state (Figure 2a,b) and frozen-solution (Figure 2c) phosphorescence spectra of Ln(TTA)3(H2O)2 (Ln = La, Gd). The spectrum of La(TTA)3(H2O)2 solid has a strong 0–0 line at 534.7 nm (18 701 cm–1) with the dominant progression frequency of 1349 cm–1, corresponding to the unresolved band comprising the antisymmetric C–F stretch and the thiophene ring stretch. The corresponding Gd3+ complex, Figure 2b, has a spectrum similar to that previously reported,23 but we assign the zero phonon line to the prominent peak at 508.5 nm (19 666 cm–1), with the progression frequency of 1350 ± 4 cm–1. The difference in zero phonon line energies for Ln = Gd, La is 965 cm–1, and from this, we estimate the triplet state energy of Eu(TTA)3(H2O)2 at ∼19 530 cm–1 (512 nm). The spectrum of Gd(TTA)3(H2O)2 in toluene at 77 K, Figure 2c, shows a blueshift of the phosphorescence from that in Figure 2b, in addition to the observation of singlet emission.
Figure 2.
Phosphorescence spectra of solid (a) La(TTA)3(H2O)2 and (b) Gd(TTA)3(H2O)2 at the nominal temperature of 10 K. (c) Fluorescence and phosphorescence spectrum of Gd(TTA)3(H2O)2 in toluene at 10 μM concentration at 77 K. Excitation wavelengths (in nm) were used as indicated. The phosphorescence spectra do not exhibit change in wavelength when the excitation wavelength is altered.
We have found that due to the magnetic/exchange properties of Gd3+, the complexes generally have short phosphorescence lifetimes. Hence, to estimate the (unquenched) triplet state lifetime for Eu(TTA)3(H2O)2, we prefer to use the lifetime for the analogous La complex, which we measured as 0.2 s at 77 K in the solid state. This value is consistent with the reported phosphorescence lifetimes of other lanthanum complexes.60 However, the magnitude represents the lowest value for the radiative lifetime, and using eq 1, it gives the highest value for the T1–S0 transition oscillator strength, Pif ∼ 6.53 × 10–9.
Europium Emission Spectrum and Its Temperature Dependence
The room-temperature22 and 77 K23 luminescence spectra of Eu(TTA)3(H2O)2 have previously been published and assigned. We note, in Figure 3a, that the room temperature spectra differ for the solid state and toluene solution, indicating a different coordination environment for Eu3+, presumably due to the loss of water in toluene solution.
Figure 3.
(a) 355 nm Excited room-temperature emission spectra of Eu(TTA)3(H2O)2: blue and black, solid, at different resolution in two instruments; red in toluene solution. The relative intensities are arbitrary for clarity of observation. (b) Temperature dependence of solid-state Eu(TTA)3(H2O)2 emission from 10 to 300 K. (c) Measured 5D0 luminescence decay curves of solid Eu(TTA)3(H2O)2 at different temperatures and (d) data plot of monoexponential lifetime versus temperature. The blue line follows y = 1/(A + B* exp(−C/0.695 × x)), with A = 2972 ± 26, B = (8.1 ± 8.6) × 106, and C = 1716 ± 211. The fit shows that other factors may be involved at lower temperatures (Radj2 = 0.9758).
Many publications employing the model of Malta have included contributions to ET rates from 7F1 because at room temperature, the occupation of this J-multiplet is appreciable. From emission spectra, the 7F1 crystal field levels of Eu(TTA)3(H2O)2 are located at 288, 358, and 493 cm–123 so that the room temperature population ratio 7F1/7F0 is estimated as 0.48 from the barycenter of 380 cm–1.
The participation of the 7F1J-multiplet in facilitating ET from an antenna to Eu3+ has been invoked in the literature1,21,28 because the SLJ selection rules forbid transfer involving 7F0. The argument is that at room temperature, where the population of 7F1 has been taken as 0.33, for example, in ref (1), it can act as an effective receiving state. Theoretically, the temperature dependence of Eu3+ 5D0 population is weak because multiphonon relaxation to the next-lowest level, 7F6, involves the energy gap of ∼12 020 cm–1, which is spanned by many phonons. Hence, if 7F1 is dominant in participating in the ET process, one would expect an increase in Eu3+ emission intensity with temperature. Figure 3b shows that, unless other factors are involved, this is not the case, and that the emission intensity shows a progressive decrease with increasing temperature. The decay of 5D0 at different temperatures is shown in Figure 3c, and the curves were fitted by monoexponential functions to give lifetimes in the region of 0.3 ms, which are plotted against temperature in Figure 3d and fitted by a single barrier model. The fit gives an activation energy of 1716 ± 211 cm–1, which is consistent with the 1749 cm–1 gap between 5D0 and 5D1 in Eu(TTA)3(H2O)2.
Oscillator Strengths of Eu3+ Transitions
The europium ion transitions are very weak in intensity. Some transitions are observed in solid Eu(TTA)3(H2O)2, as marked in Figure S2, but they are not evident in toluene solution in the same figure. We have measured the oscillator strengths by absorption spectroscopy using eq 5 for data from Eu(TTA)3(H2O)2 in toluene solution and also aqueous EuCl3. The results are listed in Table S4 together with values from other studies.
Magnitudes of Spectral Overlap Integrals
The integral in eqs 9a, 9b, and 10 is termed the spectral overlap integral. In units of energy–1, it measures the overlap of the emission band of the donor moiety with the absorption band of the acceptor. Each band is normalized to unit area. In the present case, the emission from the singlet or triplet state is very broad compared with the sharp intra-4f6 absorption transitions. The SI, Section S5, gives an example of the calculation of this integral by representing the absorption and emission bands by Gaussians (Figure S4). The value was directly calculated using Maple 2021 software.51 Alternatively, the value was calculated by summation of the intervals in the data columns,61 and the answer was in good agreement (Section S5). We have therefore employed this summation method in the present study to calculate spectral overlap integrals (Table 1). Note that the spectral overlap integral does not represent the area bounded under the donor and acceptor curves (Figure S5), which gives a much smaller answer.
Table 1. Calculated Spectral Overlap Integrals for Various Scenarios.
| systema | transitions | SO (eV–1) | Figures |
|---|---|---|---|
| GdTTA phos + EuTTA abs | T1 → S0, 7F0 → 5D1 | 2.324 | |
| GdTTA phos + EuCl3 abs | T1 → S0, 7F0 → 5D1 | 2.254 | 4a |
| GdTTA phos + EuTTA em | T1 → S0, 5D0 → 7F0 | 1.141 | 4b |
| GdTTA phos + EuTTA em | T1 → S0, 5D0 → 7F0 | 1.279 | S6a |
| GdTTA em + EuTTA abs | S1 → S0, 7F1 → 5D1 | 0.494 | 4c |
| GdTTA phos + EuTTA abs | T1 → S0, 7F1 → 5D1 | 2.317 | 4d |
| HTTA em + EuTTA em | S1 → S0, 5D0 → 7F0 | 0.232 | S6b |
| GdTTA em + EuTTA em | S1 → S0, 5D0 → 7F0 | 0.197 | S6c |
| GdTTA em + EuTTA abs | S1 → S0, 7F0 → 5D1 | 0.550 | S6d |
| HTTA em + EuCl3 abs | S1 → S0, 7F0 → 5D1 | 0.619 | S6e |
| HTTA em + EuCl3 abs | S1 → S0, 7F0 → 5D2 | 1.754 | S6f |
| GdTTA em + EuTTA exc | S1 → S0, 7F0 → 5D2 | 1.326 | S6g |
| GdTTA em + EuTTA abs | S1 → S0, 7F0 → 5D2 | 1.354 | S6h |
| GdTTA em + EuCl3 abs | S1 → S0, 7F0 → 5D3 | 1.292 | S6i |
| GdTTA em + EuCl3 abs | S1 → S0, 7F0 → 5L6 | 0.172 | S6j |
LnTTA = Ln(TTA)3(H2O)2 (Ln = Gd, Eu); phos = phosphorescence spectrum; abs = absorption spectrum; em = emission spectrum; exc excitation spectrum.
The spectral overlap integrals were calculated from normalized antenna emission and europium absorption or emission bands. The antenna triplet emission spectra were taken from solid-state Gd(TTA)3(H2O)2 phosphorescence since the energy is expected to be nearer to that of Eu(TTA)3(H2O)2, rather than that of the La3+ complex. Singlet emission spectra were taken from HTTA and Gd(TTA)3(H2O)2. The Eu3+ data were taken from the room-temperature absorption spectra of aqueous EuCl3·6H2O and solid-state and toluene-dissolved Eu(TTA)3(H2O)2, except for the 5D0–7F0 transition, which was taken from emission spectra. The calculated values do not vary much for different combinations of the above for the same overlap, showing that the assumption is reasonable, and a selection of the resulting graphs is displayed in Figures 4 and S6. In fact, the spectral overlap integrals are all small, in the narrow range of 0.17 to 2.3 eV–1 (column 3, Table 1).
Figure 4.
Examples of spectral overlap of antenna emission bands and europium absorption bands, both normalized to unity. Spectra are from this work. (a) Gd(TTA)3(H2O)2 solid-state phosphorescence spectrum (inset) and EuCl3·6H2O aqueous room-temperature absorption spectrum; (b) Gd(TTA)3(H2O)2 solid-state phosphorescence spectrum and 10 μM Eu(TTA)3(H2O)2 in toluene room-temperature emission spectrum. (c) Gd(TTA)3(H2O)2 solid-state singlet emission and Eu(TTA)3(H2O)2 solid-state room-temperature absorption spectrum. (d) Gd(TTA)3(H2O)2 solid-state phosphorescence spectrum and Eu(TTA)3(H2O)2 solid-state room-temperature absorption spectrum.
Calculated Energy Transfer Rates: Electric Dipole–Electric Dipole Mechanism
Table 2 summarizes the calculated ET rates using eq 9b. The transfer rates from the antenna triplet state to Eu3+ by this mechanism are negligible. The dominant transfer from the singlet state occurs to 5D2 and 5L6, although the back-transfer is appreciable for the latter. The maximum total ED–ED transfer rate involving the 7F0 acceptor state is 5.1 × 107 s–1, which is insufficient to quench the singlet emission. The S1–T1 intersystem crossing rate has been estimated to be typically in the order of 108 s–1,12 so that this process should dominate ED–ED ET.
Table 2. Electric Dipole–Electric Dipole Energy Transfer Rates for Eu(TTA)3(H2O)2a.
| ET transitionb | PD (ED) | PA (ED) | SO (eV–1) | ν̅av (cm–1) | WETf (s–1) | WETb (s–1) |
|---|---|---|---|---|---|---|
| T1–5D0 | 6.53E-9 | 1.66E-10 | 1.21 | 18417 | 0.001 | 2.2E-8 |
| 7.9E-8 | 0.491 | 1.1E-5 | ||||
| T1–5D1 | 6.53E-9 | 7.2E-10 | 2.29 | 19291 | 0.008 | 7.7E-4 |
| S1–5D0 | 0.05 | 1.66E-10 | 0.197 | 21357 | 956 | 9.9E-15 |
| 7.9E-8 | 4.6E5 | 4.7E-12 | ||||
| S1–5D1 | 0.05 | 7.2E-10 | 0.551 | 22231 | 1.071E4 | 1.6E-9 |
| S1–5D2 | 0.05 | 1.32E-6 | 1.335 | 23481 | 4.26E7 | 0.35 |
| 1.36E-8 | 4.39E5 | 3.63E-3 | ||||
| S1–5D3 | 0.05 | 2.74E-8 | 1.292 | 24891 | 7.62E5 | 5.1E3 |
| S1–5L6 | 0.05 | 1.82E-6 | 0.172 | 25278 | 6.53E6 | 1.83E6 |
| S1–(7F1–5D1) | 0.05 | 6.1E-8 | 0.494 | 22086 | 8.24E5 | 9.7E-9 |
| 8.5E-6 | 1.15E8 | 1.4E-6 | ||||
| T1–(7F1–5D1) | 6.53E-9 | 6.1E-8 | 2.317 | 19146 | 0.67 | 0.02 |
| 8.5E-6 | 94 | 2.8 |
PD and PA are the donor and acceptor ED oscillator strengths. SO is the spectral overlap integral and ν̅av is the donor–acceptor average energy. WETf and WET are, respectively, the forward and backward rates according to the Boltzmann equation. The distance R in eq 9b was fixed at 4.5 Å as discussed above.21 Only the ED contribution to the oscillator strength of 7F0 → 5D1 has been considered. The ED-MD (MD = magnetic dipole) ET rate is zero for a centrosymmetric system62 and is expected to be small in other cases.54 The oscillator strength of S1 → S0 is given as 0.05, which is probably 1 order of magnitude too high (SI, Section S3), and if so, the calculated WET then needs to be reduced by a factor of 10. Alternative oscillator strengths are given for 7F0 → 5D0 and the hypersensitive 7F0 → 5D2 transition, according to the data in Table S4.
The initial Eu3+ state is 7F0 unless indicated, and the final antenna state is S0.
The appreciable population of 7F1 at room temperature leads to its participation in the ET processes. Two values are listed for the oscillator strength of the ED-allowed transition 7F1 → 5D1 in Table 2, taken from Table S4. The spectral overlaps are displayed for the ligand singlet and triplet transitions involving 7F1 at room temperature in Figure 4c,d, respectively, and the singlet channel is much faster (Table 2) for the ED–ED mechanism. Processes involving 7F1 → 5D0 (Figure S6k,l) are not considered here because the ED intensity of this transition is very weak.
Electric Dipole–Electric Quadrupole (ED–EQ) ET Mechanism
The antenna singlet and triplet transitions may follow orbitally allowed ED transitions. Besides forced ED pure electronic transitions and vibronically allowed ED transitions, some transitions of Ln3+ may be EQ allowed. However, the spectral intensity of such transitions is very weak. By contrast, relative to ED–ED ET, the ED–EQ ET mechanism may occur, for fully allowed ED and EQ transitions, respectively, with the ratio about (a0/R)2,52,54 where a0 is the Bohr radius (5.291772...× 10–11 m) and R is the donor–acceptor separation, as above. For R ∼ 4.5 Å, this ratio is 0.014, so ED–ED ET is more important. However, the 4fN – 4fN transitions of Ln3+ are usually not first-order ED-allowed and are rather weaker. Taking the 7F0 → 5D2 transition as an example because it is the most intense EQ allowed transition considered herein, eq 14 gives the ratio P(ED–EQ)/P(ED–ED) of 73 so that the ED–EQ ET mechanism in this case can give a rate up to ∼3.0 × 109 s–1. The use of eq 12b (with the oscillator strength of the EQ acceptor transition 7F0 → 5D2 (6.7 × 10–12)55 inserted into eq 11b) gives the result 3.9 × 108 s–1, which is similar to the decay rate of S1 → S0.
In summary, the combined ED–EQ and ED–ED rates from the S1 state can therefore account for the quenching of singlet emission. The ET contributions from the triplet state to Eu3+ by the above mechanisms are very small, leading to its common description of “Dexter ET”.
Rate Equation Approach
We apply an independent systems model to calculate the energy transfer rate to Eu3+ in Eu(TTA)3(H2O)2. This means that the overall metal–ligand transitions are considered independently and concurrently so that sensible ground-state populations are conserved. Seven levels are included. The antenna levels are S1, T1, and S0. Other levels such as Tn were found to be of minor importance here. The Eu3+ levels are labeled DJ that include 5L6, 5D3, and 5D2 combined; 5D1, 5D0, and 7F0. The latter comprises 7F0 and 7F1 for simplicity here, but we have also performed calculations using separate levels. However, we have taken into account that the occupations of 7F0 and 7F1 are about 0.6 and 0.4 at room temperature, but 1.0 and 0.0, respectively, at 10 K. The rate constants are listed in Table 3. From the above temperature dependence of 5D0 lifetime, we are confident that a charge transfer state is not involved in the energy transfer processes. The relevant experimental data for Eu(TTA)3(H2O)2 have been previously published (Figure 5).8
Table 3. Rate Constants, Their Meanings, and Values Adopted in the Calculations.
| rate constanta | meaning | value 300 K | value 10 K |
|---|---|---|---|
| Q | S0 → S1 excitation | 10 | 10 |
| a | T1 → S0 nonradiative and radiative decay | 1E6 | 1E2 |
| b | S1 → S0 fluorescence decay | 3E8 | 3E8 |
| f | S1 → T1 intersystem crossing | 1E9 | 1E9 |
| c | 5D0 → 7FJ luminescence | 5000 | 3906 |
| g | S1 → S07F0 → DJ energy transfer | 1E9 | 1E9 |
| k | S1 → S07F0 → 5D1 energy transfer | 1.1E8 | 1.1E4 |
| m | S1 → S07F0 → 5D0 energy transfer | 1.17E6 | 4.6E5 |
| n | T1 → S07F0 → 5D1 energy transfer | 3.33E7 | 2.84E7 |
| p | T1 → S0 F0 → 5D0 energy transfer | 1.5E7 | 1.5E7 |
| s | DJ → 5D1 internal conversion | 1E8 | 1E8 |
| d | 5D1 → 5D0 internal conversion | 2.5E6 | 2.5E5 |
| u | 5D1 → 7FJ luminescence | 1E4 | 1.5E5 |
Unit s–1 or mol–1 s–1.
Figure 5.

Rate constants in the independent systems model.
The rate equations considered are as follows:
 |
These equations were solved in Maple 202151 by the Rosenbrock method with the initial concentrations of [S0] = 1, [7F0] = 1, and others zero. The concentrations at 5 ns were determined, and these were employed in the further calculation with zero excitation (Q = 0). The rationale for parameter values is given in SI, Section S7. The values are representative, and we have not made an effort to fine-tune them to simulate experimental data.
The first calculations assumed, as often done, that the energy transfer to Eu3+ arises solely from the triplet state. In this case, the rate parameters k, m, and g were set to zero. The 300 K risetime of 5D1 from Figure 4 in ref (8) is ∼30 ns, which infers an ET rate (parameter n) of 3.33 × 107 s–1 if the transfer is only from T1. The 300 K decay time of 5D1 is 0.4 μs.8 Using the other illustrative values in Table 3, for this zero singlet ET scenario (Szero), the calculated concentrations of the different states are plotted against time in Figure S7 (black lines) and subsequently fitted by mono- or biexponential functions (red lines). The calculated risetime of 5D1 was found to be 20 ns, which is the same as the triplet decay time. To simulate 10 K conditions, the calculation was repeated with the contributions to energy transfer from 7F1 omitted, Figure S8 (Table 3, column 4, also with the 5D1 and 5D0 lifetimes adjusted for their temperature dependence). Again, the 5D1 risetime equals the triplet decay time, but it only increases to 23 ns, far from the experimental value ∼70 ns as in Figure 4b, ref (8). We therefore consider that other parameters would need to change to achieve a longer risetime but reducing the intersystem crossing rate (f) by a factor of 10 from 300 to 10 K has little effect upon the 5D1 risetime (Figure S9) and increasing parameter a to 106 s–1 has no effect (Figure S10).
An alternative model involves ET from solely the singlet state (the Tzero model), as displayed in Figure S11 for 300 K. Again, there is a 5D1 risetime in the ns range, in this case 10 ns. By comparison with the previous Szero model, this leads to the conclusion that the experimental observation of a ns risetime for 5D1 does not enable one to judge if the ET route involves singlet or triplet ET, let alone the operating mechanism, as has often been done. Taking into account the changes in 5D0 and 5D1 lifetimes and the absence of ET involving 7F1, the 10 K profiles are shown in Figure S12 and the 5D1 risetime does not differ from that at room temperature. However, if the internal conversion rate (parameter s) is reduced by a factor of 10 as in Figure S13, which is reasonable for such a temperature change, the 5D1 risetime increases up to 102 ns. This could be a signature of mainly singlet energy transfer.
The two above models, Szero and Tzero, show that the feeder state, T1 or 5D2, determines the 5D1 risetime and that while, from 300 to 10 K, a 10-fold change of 5D2–5D1 internal conversion rate is reasonable and produces a longer risetime, the change of rate involving T1 only slightly modifies the risetime. Hence, in principle, we can distinguish singlet or triplet ET by monitoring the change in 5D1 risetime with temperature.
Figure 6 displays the ET scenario from ligand to Eu3+ at 300 K with combined singlet and triplet energy transfer as in columns 3 and 7, Table 3: 96% from S1 and 4% from T1. Remember that the exchange contribution to T1 is not known, but we can put an upper limit on it from the 5D1 risetime.
Figure 6.
Calculated (black lines) 300 K time profiles of levels using the Rosenbrock method, following a 5 ns pulse. (a) 5D0; (b) 5D1; (c) DJ; (d) T1; (e) S1; (f) S0; (g) 7F0. The parameters are in columns 3 and 7 of Table 3. The red lines are fits to the calculated data using mono- or biexponential functions, with the fitted lifetimes as indicated. In S0 and F0: A 1.000000002; B 0.9999999948; C 0.999999988; D 0.9999999811; E 1.000000003; F 0.999999993; G 0.9999999835; H 0.9999999739; I 0.9999999643.
The 5D1 risetime is intermediate (14 ns) between the Szero and Tzero models. The profile for 7F0 is interesting because it displays both the nanosecond decrease (as in Szero) and the long risetime as in Tzero. The latter is determined by 5D0 decay, whereas the former is the same as the T1 decay time and the S0 risetime. Monitoring the population of 7F0 (although difficult) may therefore be fruitful when considering energy transfer mechanisms.
Using the parameters in Table 3, columns 4 and 8, to simulate the 10 K kinetics (Figure S14), the 5D1 risetime is intermediate between the decay times of 5D2 (DJ) and T1 but is similar to the room temperature value. However, taking into account the slowing of the 5D2–5D1 internal conversion rate by an order of magnitude from 300 to 10 K (with rate constant s changed in Table 3, column 8, to 107 s–1, Figure 7), the 5D1 risetime becomes much longer.
Figure 7.
Calculated 10 K time profiles of levels using the Rosenbrock method, following a 5 ns pulse (black lines). (a) 5D0; (b) 5D1; (c) DJ; (d) T1; (e) S1; (f) S0; (g) 7F0. The parameters are in columns 4 and 8 of Table 3, with the exception that s = 107 s–1. The red lines are fits to the calculated data using mono- or biexponential functions, with the fitted lifetimes as indicated. In S0 and F0: A 1.000000002; B 0.9999999948; C 0.999999988; D 0.9999999811; E 0.9999999788; F 0.9999999708; G 0.9999999629.
We summarize the results from the model as follows:
-
1.
The maximum total ET rate from the ligand singlet state to the acceptor 7F0 state via the ED–ED mechanism is of the order 107 s–1. The rate involving the acceptor state 7F1 is up to the order 108 s–1. The intensity of Eu3+ emission decreases with increasing temperature despite an increasing ET rate involving the 7F1 acceptor state. The maximum rate for ED–EQ transfer (108–109 s–1) is sufficient to quench the singlet emission. We are presently unable to calculate the ET rate for exchange interaction but our calculations of the 5D1 risetime indicate a value in the range of 107 s–1.
-
2.
The ET rate from the triplet state by ED–ED and ED–EQ mechanisms is very weak but is still enough to quench the long lifetime triplet emission.
-
3.
The observation of a nanosecond risetime for 5D1 does not enable distinction of triplet or singlet ET, let alone the mechanism. The 5D1 risetime may be contributed by several processes.
-
4.
Following the 5D1 risetime as a function of temperature and using the temporal profile of 7F0 may provide useful information concerning the energy transfer route.
Conclusions
We have employed the Dexter formalism54 to investigate the ET mechanisms and rates from an antenna to a lanthanide ion, with the complex Eu(TTA)3(H2O)2 as a case study. This compound may not have been a good choice in view of its rapid decomposition in moist air, but our spectra are consistent with those of previous studies. Considerable differences exist between the spectra for the complex in the solid state and in dilute solution. These arise from the enormous concentration factor in the solid state and merit further study. The use of the experimental data for oscillator strengths and spectral overlap enables ET rates to be calculated for ED–ED and ED–EQ ET. As previously shown,61 the Förster and Dexter formalisms are the same for ED–ED transfer, with the exception of local field effects. The independent systems model is successful in reproducing the temporal variation of experimental data. The model can be applied on different timescales and is general for Eu3+ complexes except for special cases, such as the involvement of a charge transfer state, where the model can be further adapted by its inclusion. This study does show that time-gated spectroscopy together with transient absorption measurements could provide detailed information to understand the kinetics of energy transfer in Eu3+ complexes.
In the Supporting Information, we have commented upon the software LUMPAC and JOYSpectra, which both use the model of Malta. We consider that the use of an approximation for the exchange integral and a fixed value may not be justified. The major outstanding problem therefore lies with the calculation of exchange ET rate. Some previous reports have considered the evaluation of two-center exchange integrals, and we will study these to apply the formalism of Dexter and calculate the exchange contribution to ET.
Acknowledgments
K.-L.W. acknowledges funding from the Hong Kong Research Grants Council Research Grant No. 1230020. The authors thank the Max-Planck-Institut für Chemische Energiekonversion for making available the Orca Program. This research was conducted using the resources of the High Performance Cluster Computing Center, Hong Kong Baptist University, which receives funding from the Research Grant Council, University Grant Committee of the HKSAR and Hong Kong Baptist University. The authors also thank Sci-Hub for removing barriers in the way to science. They also thank Dr. Jose Diogo de Lisboa Dutra for private discussions concerning LUMPAC and Prof. O.L. Malta and his group for correspondence. Professor Y. Y. Yeung is thanked for providing the free ion compositions of multiplet terms of some europium complexes.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.2c03965.
Experimental (S1); computation of molecular structure (S2); singlet energy and oscillator strength (S3); oscillator strengths (S4); spectral overlap integral (S5); spectral overlap diagrams (S6); rate equation model (S7); calculations using the model of Malta (S8); units and conversions used in this work (S9); and references (S10) (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Kasprzycka E.; Trush V. A.; Amirkhanov V. M.; Jerzykiewicz L.; Malta O. L.; Legendziewicz J.; Gawryszewska P. Contribution of Energy Transfer from the Singlet State to the Sensitization of Eu3+ and Tb3+ Luminescence by Sulfonylamidophosphates. Chem. – Eur. J. 2017, 23, 1318–1330. 10.1002/chem.201603767. [DOI] [PubMed] [Google Scholar]
- Carlos L. D.; Faustino W. M.; Malta O. L. Comment on Trivalent Europium Lifetimes in the Presence of Intramolecular Energy Transfer Processes. J. Braz. Chem. Soc. 2008, 19, 299–301. 10.1590/S0103-50532008000200015. [DOI] [Google Scholar]
- Yang C.; Fu L.-M.; Wang Y.; Zhang J.-P.; Wong W.-T.; Ai X.-C.; Qiao Y.-F.; Zou B.-S.; Gui L.-L. A Highly Luminescent Europium Complex Showing Visible-Light-Sensitized Red Emission: Direct Observation of the Singlet Pathway. Angew. Chem., Int. Ed. 2004, 43, 5010–5013. 10.1002/anie.200454141. [DOI] [PubMed] [Google Scholar]
- Miyazaki S.; Miyata K.; Sakamoto H.; Suzue F.; Kitagawa Y.; Hasegawa Y.; Onda K. Dual Energy Transfer Pathways from an Antenna Ligand to Lanthanide Ion in Trivalent Europium Complexes with Phosphine-Oxide Bridges. J. Phys. Chem. A 2020, 124, 6601–6606. 10.1021/acs.jpca.0c02224. [DOI] [PubMed] [Google Scholar]
- Fu L.-M.; Ai X.-C.; Li M.-Y.; Wen X.-F.; Hao R.; Wu Y.-S.; Wang Y.; Zhang J.-P. Role of Ligand-to-Metal Charge Transfer State in Nontriplet Photosensitization of Luminescent Europium Complex. J. Phys. Chem. A 2010, 114, 4494–4500. 10.1021/jp9103189. [DOI] [PubMed] [Google Scholar]
- Mara M. W.; Tatum D. S.; March A.-M.; Doumy G.; Moore E. G.; Raymond K. N. Energy Transfer from Antenna Ligand to Europium(III) Followed Using Ultrafast Optical and X-Ray Spectroscopy. J. Am. Chem. Soc. 2019, 141, 11071–11081. 10.1021/jacs.9b02792. [DOI] [PubMed] [Google Scholar]
- Gawryszewska P.; Moroz O. V.; Trush V. A.; Amirkhanov V. M.; Lis T.; Sobczyk M.; Siczek M. Spectroscopy and Structure of LnIII Complexes with Sulfonylamidophosphate-Type Ligands as Sensitizers of Visible and Near-Infrared Luminescence. ChemPlusChem 2012, 77, 482–496. 10.1002/cplu.201200026. [DOI] [Google Scholar]
- Faustino W. M.; Nunes L. A.; Terra I. A. A.; Felinto M. C. F. C.; Brito H. F.; Malta O. L. Measurement and Model Calculation of the Temperature Dependence of Ligand-to-Metal Energy Transfer Rates in Lanthanide Complexes. J. Lumin. 2013, 137, 269–273. 10.1016/j.jlumin.2013.01.008. [DOI] [Google Scholar]; Note the error in this publication: in the caption of Figure 4 (μs is written instead of ns) and the color coding in the Figure 4b needs to be reversed.
- Lis S.; Elbanowski M.; Makowska B.; Hnatejko Z. Energy Transfer in Solution of Lanthanide Complexes. J. Photochem. Photobiol., A 2002, 150, 233–247. 10.1016/S1010-6030(01)00637-2. [DOI] [Google Scholar]
- Tanaka F.; Ishibashi T. Energy Transfer between Lanthanide Ions in Dinuclear Complexes. J. Chem. Soc., Faraday Trans. 1996, 92, 1105–1110. 10.1039/ft9969201105. [DOI] [Google Scholar]
- Wang J.; Deng R. Energy Transfer in Dye-Coupled Lanthanide-Doped Nanoparticles: From Design to Application. Chem. – Asian J. 2018, 13, 614–625. 10.1002/asia.201701817. [DOI] [PubMed] [Google Scholar]
- Carneiro Neto A. N.; Teotonio E. E. S.; de Sá G. F.; Brito H. F.; Legendziewicz J.; Carlos L. D.; Felinto M. C. F. C.; Gawryszewska P.; Moura R. T. Jr.; Longo R. L.. et al. Modeling Intramolecular Energy Transfer in Lanthanide Chelates: A Critical Review and Recent Advances. In Handbook on the Physics and Chemistry of Rare Earths, Including Actinides; Elsevier, 2019; Vol. 56, pp 55–162. [Google Scholar]
- Moore E. G.; Samuel A. P. S.; Raymond K. N. From Antenna to Assay: Lessons Learned in Lanthanide Luminescence. Acc. Chem. Res. 2009, 42, 542–552. 10.1021/ar800211j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vallet V.; Fischer A.; Szabó Z.; Grenthe I. The Structure and Bonding of Y, Eu, U, Am and Cm Complexes as Studied by Quantum Chemical Methods and X-Ray Crystallography. Dalton Trans. 2010, 39, 7666–7672. 10.1039/b926508b. [DOI] [PubMed] [Google Scholar]
- White J. G. The Crystal Structure of Europium Tris[4,4,4,-trifluoro-1-(2-thienyl)-1,3-butanedione] Dihydrate. Inorg. Chim. Acta 1976, 16, 159–162. 10.1016/S0020-1693(00)91705-5. [DOI] [Google Scholar]
- Malta O. L. Ligand-Rare-Earth Ion Energy Transfer in Coordination Compounds. A Theoretical Approach. J. Lumin. 1997, 71, 229–236. 10.1016/S0022-2313(96)00126-3. [DOI] [Google Scholar]
- Malta O. L. Mechanisms of Non-Radiative Energy Transfer Involving Lanthanide Ions Revisited. J. Non-Cryst. Solids 2008, 354, 4770–4776. 10.1016/j.jnoncrysol.2008.04.023. [DOI] [Google Scholar]
- Malta O. L.; Gonçalves e Silva F. R. A Theoretical Approach to Intramolecular Energy Transfer and Emission Quantum Yields in Coordination Compounds of Rare Earth Ions. Spectrochim. Acta, Part A 1998, 54, 1593–1599. 10.1016/S1386-1425(98)00086-9. [DOI] [Google Scholar]
- Kushida T. Energy Transfer and Cooperative Optical Transitions in Rare-Earth Doped Inorganic Materials. I. Transition Probability Calculation. J. Phys. Soc. Jpn. 1973, 34, 1318–1326. 10.1143/JPSJ.34.1318. [DOI] [Google Scholar]
- Dutra J. D. L.; Bispo T. D.; Freire R. O. LUMPAC Lanthanide Luminescence Software: Efficient and User Friendly. J. Comput. Chem. 2014, 35, 772–775. 10.1002/jcc.23542. [DOI] [PubMed] [Google Scholar]
- Moura R. T. Jr.; Carneiro Neto A. N.; Aguiar E. C.; Santos-Jr C. V.; de Lima E. M.; Faustino W. M.; Teotonio E. E. S.; Brito H. F.; Felinto M. C. F. C.; Ferreira R. A. S.; et al. JOYSpectra: A Web Platform for Luminescence of Lanthanides. Opt. Mater.: X 2021, 11, 100080. 10.1016/j.omx.2021.100080. [DOI] [Google Scholar]
- Malta O. L.; Brito H. F.; Menezes J. F. S.; Gongalves e Silva F. R.; Alves S. Jr.; Farias F. S. Jr.; de Andrade A. V. M. Spectroscopic Properties of a New Light-Converting Device Eu(Thenoyltrifluoroacetonate)32(Dibenzyl Sulfoxide). A Theoretical Analysis Based on Structural Data Obtained from A Sparkle Model. J. Lumin. 1997, 75, 255–268. 10.1016/S0022-2313(97)00107-5. [DOI] [Google Scholar]
- Teotonio E. E. S.; Brito H. F.; Felinto M. C. F. C.; Kodaira C. A.; Malta O. L. Luminescence Investigations on Eu(III) Thenoyltrifluoroacetonate Complexes with Amide Ligands. J. Coord. Chem. 2003, 56, 913–921. 10.1080/0095897031000135333. [DOI] [Google Scholar]
- Charles R. G.; Ohlmann R. C. Europium thenoyltrifluoroacetonate, Preparation and Fluorescence Properties. J. Inorg. NucI. Chem. 1965, 27, 255–259. 10.1016/0022-1902(65)80222-6. [DOI] [Google Scholar]
- Fernandes M.; de Zea Bermudez V.; Sá Ferreira R. A.; Carlos L. D.; Charas A.; Morgado J.; Silva M. M.; Smith M. J. Highly Photostable Luminescent Poly(ε-caprolactone)siloxane Biohybrids Doped with Europium Complexes. Chem. Mater. 2007, 19, 3892–3901. 10.1021/cm062832n. [DOI] [Google Scholar]
- Zhou L.; Zhang H.; Deng R.; Li Z.; Yu J.; Guo Z. Conversion Process of the Dominant Electroluminescence Mechanism in a Molecularly Doped Organic Light-Emitting Device with Only Electron Trapping. J. Appl. Phys. 2007, 102, 064504. 10.1063/1.2779269. [DOI] [Google Scholar]
- Zucchi G.; Murugesan V.; Tondelier D.; Aldakov D.; Jeon T.; Yang F.; Thuéry P.; Ephritikhine M.; Geffroy B. Solution, Solid State, and Film Properties of a Structurally Characterized Highly Luminescent Molecular Europium Plastic Material Excitable with Visible Light. Inorg. Chem. 2011, 50, 4851–4856. 10.1021/ic2000415. [DOI] [PubMed] [Google Scholar]
- Blois L.; Carneiro Neto A. N.; Malta O. L.; Brito H. F. The Role of the Eu3+ 7F1 Level in the Direct Sensitization of the 5D0 Emitting Level through Intramolecular Energy Transfer. J. Lumin. 2022, 247, 118862. 10.1016/j.jlumin.2022.118862. [DOI] [Google Scholar]
- Neese F. The ORCA Program System. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 73–78. 10.1002/wcms.81. [DOI] [Google Scholar]
- Neese F. Software Update: the ORCA Program System, Version 4.0. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1327 10.1002/wcms.1327. [DOI] [Google Scholar]
- Avogadro: An Open-Source Molecular Builder and Visualization Tool. Version 1.2.0. http://avogadro.cc/ (Accessed on 18 August 2022).
- Hanwell M. D.; Curtis D. E.; Lonie D. C.; Vandermeersch T.; Zurek E.; Hutchison G. R. Avogadro: An Advanced Semantic Chemical Editor, Visualization, and Analysis Platform. J. Cheminf. 2012, 4, 17 10.1186/1758-2946-4-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allouche A.-R. Gabedit-A Graphical User Interface for Computational Chemistry Softwares. J. Comput. Chem. 2011, 32, 174–182. 10.1002/jcc.21600. [DOI] [PubMed] [Google Scholar]
- a Perdew J. P. Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B 1986, 33, 8822–8824. 10.1103/PhysRevB.33.8822. [DOI] [PubMed] [Google Scholar]; b Erratum: Phys. Rev. B 1986, 34, 7406.
- a Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]; b Erratum: Phys. Rev. Lett. 1997, 78, 1396.
- Weigend F.; Ahlrichs R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- Andrae D.; Haeussermann U.; Dolg M.; Stoll H.; Preuss H. Energy-Adjusted ab Initio Pseudopotentials for the Second and Third Row Transition Elements. Theor. Chim. Acta 1990, 77, 123–144. 10.1007/BF01114537. [DOI] [Google Scholar]
- Dolg M.; Stoll H.; Savin A.; Preuss H. Energy-Adjusted Pseudopotentials for the Rare Earth Elements. Theor. Chim. Acta 1989, 75, 173–194. 10.1007/BF00528565. [DOI] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Garcia-Ratés M.; Neese F. Efficient Implementation of the Analytical Second Derivatives of Hartree-Fock and Hybrid DFT Energies within the Framework of the Conductor-Like Polarizable Continuum Model. J. Comput. Chem. 2019, 40, 1816–1828. 10.1002/jcc.25833. [DOI] [PubMed] [Google Scholar]
- Angeli C.; Cimiraglia R.; Evangelisti S.; Leininger T.; Malrieu J.-P. Introduction of N-electron Valence States for Multireference Perturbation Theory. J. Chem. Phys. 2001, 114, 10252–10264. 10.1063/1.1361246. [DOI] [Google Scholar]
- Angeli C.; Cimiraglia R.; Malrieu J.-P. N-electron Valence State Perturbation Theory: A Fast Implementation of the Strongly Contracted Variant. Chem. Phys. Lett. 2001, 350, 297–305. 10.1016/S0009-2614(01)01303-3. [DOI] [Google Scholar]
- Angeli C.; Cimiraglia R.; Malrieu J.-P. N-electron Valence State Perturbation Theory: A Spinless Formulation and an Efficient Implementation of the Strongly Contracted and of the Partially Contracted Variants. J. Chem. Phys. 2002, 117, 9138–9153. 10.1063/1.1515317. [DOI] [Google Scholar]
- Hehre W. J.; Ditchfield R.; Pople J. A. Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. 10.1063/1.1677527. [DOI] [Google Scholar]
- Hellweg A.; Hattig C.; Hofener S.; Klopper W. Optimized Accurate Auxiliary Basis Sets for RI-MP2 and RI-CC2 Calculations for the Atoms Rb to Rn. Theor. Chem. Acc. 2007, 117, 587–597. 10.1007/s00214-007-0250-5. [DOI] [Google Scholar]
- Lu T.; Chen F. Multiwfn: A Multifunctional Wavefunction Analyser. J. Comput. Chem. 2012, 33, 580–592. 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- Diamond–Crystal and Molecular Structure Visualization. http://www.crystalimpact.com/diamond (Accessed on 18 August 2022).
- Tanner P. A.; Yeung Y. Y.; Ning L. What Factors Affect the 5D0 Energy of Eu3+? An Investigation of Nephelauxetic Effects. J. Phys. Chem. A 2013, 117, 2771–2781. 10.1021/jp400247r. [DOI] [PubMed] [Google Scholar]
- Kasprzycka E.; Carneiro Neto A. N.; Trush V. A.; Jerzykiewicz L.; Amirkhanov V. M.; Malta O. L.; Legendziewicz J.; Gawryszewska P. How Minor Structural Changes Generate Major Consequences in Photophysical Properties of RE Coordination Compounds; Resonance Effect, LMCT State. J. Rare Earths 2020, 38, 552–563. 10.1016/j.jre.2020.02.001. [DOI] [Google Scholar]
- Maple . Maplesoft; A Division of Waterloo Maple Inc.: Waterloo, Ontario, 2021.
- Henderson B.; Imbusch G. F.. Optical Spectroscopy of Inorganic Solids; Oxford University Press: Oxford, U.K., 1989. [Google Scholar]
- Hilborn R. C. Einstein Coefficients, Cross Sections, f Values, Dipole Moments and All That. Am. J. Phys. 1982, 50, 982–986. 10.1119/1.12937. [DOI] [Google Scholar]
- Dexter D. L. A Theory of Sensitized Luminescence in Solids. J. Chem. Phys. 1953, 21, 836–850. 10.1063/1.1699044. [DOI] [Google Scholar]
- Dodson C. M.; Zia R.. Magnetic Dipole and Electric Quadrupole Transitions in the Trivalent Lanthanide Series: Calculated Emission Rates and Oscillator Strengths; Oxford University Press: Oxford, U.K., 1989. [Google Scholar]
- Bernath P. F. MoLLIST: Molecular Line Lists, Intensities and Spectra. J. Quant. Spectrosc. Radiat. Transfer 2020, 240, 106687 10.1016/j.jqsrt.2019.106687. [DOI] [Google Scholar]
- Reid M. F.Transition Intensities, Chapter 2, In Crystal Field Handbook; Cambridge University Press: Cambridge, 2000; Vol. 190. [Google Scholar]
- Tanner P. A. Spectra, Energy Levels and Energy Transfer in High Symmetry Lanthanide Compounds. Top. Curr. Chem. 2004, 241, 167–278. [Google Scholar]
- Rajamouli B.; Devi R.; Mohanty A.; Krishnan V.; Vaidyanathan S. Effects of Electron-Withdrawing Groups in Imidazole-Phenanthroline Ligands and Their Influence on the Photophysical Properties of EuIII Complexes for White Light-Emitting Diodes. New J. Chem. 2017, 41, 9826–9839. 10.1039/C7NJ02291C. [DOI] [Google Scholar]
- Brinen J. S.; Halverson F.; Leto J. R. Photoluminescence of Lanthanide Complexes. IV. Phosphorescence of Lanthanum Compounds. J. Chem. Phys. 1965, 42, 4213–4219. 10.1063/1.1695922. [DOI] [Google Scholar]
- Tanner P. A.; Zhou L.; Duan C.-K.; Wong K.-L. Misconceptions in Electronic Energy Transfer: Bridging the Gap between Chemistry and Physics. Chem. Soc. Rev. 2018, 47, 5234–5265. 10.1039/C8CS00002F. [DOI] [PubMed] [Google Scholar]
- Chua M.; Tanner P. A.; Reid M. F. Energy Transfer by Electric Dipole-Magnetic Dipole Interaction in Cubic Crystals. Solid State Commun. 1994, 90, 581–583. 10.1016/0038-1098(94)90125-2. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.








