Abstract
Cancer starts after initially healthy tissue cells accumulate several specific mutations or other genetic alterations. The dynamics of tumor formation is a very complex phenomenon due to multiple involved biochemical and biophysical processes. It leads to a very large number of possible pathways on the road to final fixation of all mutations that marks the beginning of the cancer, complicating the understanding of microscopic mechanisms of tumor formation. We present a new theoretical framework of analyzing the cancer initiation dynamics by exploring the properties of effective free-energy landscape of the process. It is argued that although there are many possible pathways for the fixation of all mutations in the system, there are only a few dominating pathways on the road to tumor formation. The theoretical approach is explicitly tested in the system with only two mutations using analytical calculations and Monte Carlo computer simulations. Excellent agreement with theoretical predictions is found for a large range of parameters, supporting our hypothesis and allowing us to better understand the mechanisms of cancer initiation. Our theoretical approach clarifies some important aspects of microscopic processes that lead to tumor formation.
Significance
Cancer results from accumulation of several unfavorable mutations in tissues over the course of human lifetimes. Understanding how such mutations fixate during a lifetime is critically important for clarifying the underlying mechanisms of tumor formation. Inspired by the analysis of stochastic processes in chemistry and physics, we developed a new theoretical framework to investigate the dynamics of cancer initiation. Our analysis reveals that despite a large number of possible dynamic pathways, there are only a few optimal pathways that govern the formation of the tumor. This approach should help in analyzing the mechanisms of cancer initiation as well as in the development of new medical anticancer methods.
Introduction
Cancer is a collection of genetically related diseases that exhibit uncontrolled cellular growth in specific tissues that strongly affects the normal functioning of living organisms and might even lead to a death (1,2). It is now well established that the cause of cancer is the accumulation of several specific genetic or epigenetic alterations in the genome (1, 2, 3, 4). The genetic errors frequently appear during cell replications, but a huge majority of them are quickly repaired by specific biochemical DNA repair pathways (2,5,6). Due to the stochastic nature of these chemical processes, a very small fraction of these mutations might escape the repair mechanisms, and the accumulation of several such mutations eventually can lead to a cancer. However, the microscopic details of how the tumors develop still remain not well understood despite significant efforts in multiple research areas (7,8).
It is clear that tumor formation is the result of a complex network of chemical, biological, and physical processes (1,9). Each type of the cancer is initiated by acquisition of a relatively small number of specific mutations or other genetic alterations (typically between two and eight).
In recent years, several theoretical approaches to analyze the dynamics of cancer initiation have been proposed (10, 11, 12, 13, 14, 15). Many of them specifically addressed the effect of stochastic tunneling (12,16, 17, 18), showing the importance of this phenomenon. For example, it was found that stochastic tunneling is a leading process in adaptation dynamics of asexual populations across fitness valleys (19, 20, 21). However, despite significant advances in our understanding of the cancer initiation dynamics, the main difficulty is that the overall process of multiple mutations fixation has a very large number of possible pathways. This leads to the use of several approximations that are not always able to realistically describe the processes that stimulate tumor formation.
In this paper, we present a new theoretical approach of analyzing the cancer initiation dynamics. It is based on analogy with the analysis of complex processes in physics and chemistry, suggesting exploring the effective free-energy description of the fixation dynamics for several mutations. The method is explicitly applied for the system with two mutations where it is tested with analytical calculations and Monte Carlo computer simulations. It is found that there are only a few pathways that dominate the fixation process. This significantly simplifies the overall analysis, and it allows to understand better the underlying microscopic mechanisms of tumor formation. The extension of these theoretical method to systems with multiple mutations is also discussed. It is interesting to note that our idea is related to a recently proposed method of analyzing stochastic systems that takes into account their topological properties (22).
Methods
The cancer initiation involves various processes such as the appearance of mutations, multiple cell divisions, and cell deaths (23). Although the system starts with one of the normal cells becoming mutated, the tumor formation is associated with the situation when all cells in the tissue acquire all mutations, which is known as a mutation fixation. The important critical constraint for all processes in the system is that due to homeostasis the total number of cells in the tissue is always fixed. The main idea of our method is to look at the cancer initiation process at steady-state conditions as a motion of a “particle” in an effective free-energy landscape created by transitions between different stochastic states. The “particle” corresponds to a current state of the system, which is determined by the number of cells with different degrees of mutations. The effective free-energy landscape is built in the following way. Since all transition rates out of the given state can be specified, one can evaluate the residence times in each state. We are considering the systems in the stationary state, i.e., as soon as the total fixation is achieved, the process immediately starts from the beginning. This eliminates any free-energy bias between the initial and final states of the system. Then the inverse of the residence time correlates with effective free-energy for this state. This is because the longer the system is occupying the given state, the lower is the corresponding “free energy.” Finally, the cancer initiation process is viewed as a motion in this effective potential between initial and end states. The initial state has one mutated cell with only one mutation, and the final state has all cells with all possible mutations. The analysis of stochastic dynamics in free-energy landscapes has been widely explored for understanding the mechanisms of various complex processes in chemistry, physics, and biology (24,25).
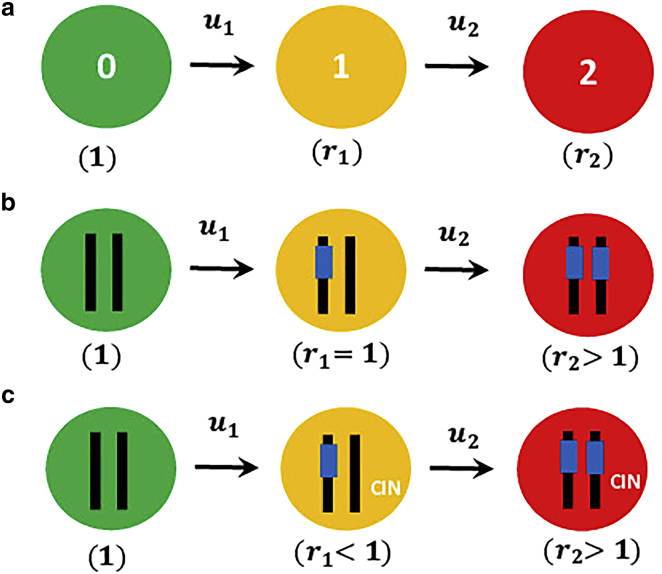
Let us explain in more detail the hypothesis by concentrating on a simplest nontrivial “two-hit” model of cancer initiation dynamics (26,27). In this model, which is schematically shown in Fig. 1 a, the system might be without any mutations in the tissue cells (indicated by the green circle), or it might sequentially acquire one mutation in some of the cells (indicated by the yellow circle), and it might finally get two mutations in all tissue cells (indicated by red circle). Two specific examples of the processes that might follow the “two-hit” model, inactivation of tumor suppressor genes and chromosomal instability, are presented in Fig. 1 b and c (3).
Figure 1.
(a) A schematic description for cancer initiation dynamics in the “two-hit” model. First and second mutations can appear with rates and , respectively. The fitness parameters for normal, one-mutation and two-mutation cells are 1, , and , respectively. (b) A schematic view for the process of inactivation of tumor suppressor genes that might follow the “two-hit” model. In this case, introducing first mutation does not affect the fitness parameter (), whereas acquiring the second mutation would increase the cell proliferation rate (). (c) A schematic view of the chromosomal instability (CIN) process that also might follow the “two-hit” model (28). Here, the first mutation by itself is known to be disadvantageous (), whereas introducing the second mutation would make their combination advantageous (). To see this figure in color, go online.
The total number of cells in the tissue is assumed to be equal to N, and it is constant during the cancer initiation process (3). This is one of the features of homeostasis that keeps the number of cells in healthy adult tissues to be constant (3). As illustrated in Fig. 1 a, there are three types of tissue cells that can be found in the system: normal cells without mutations (type 0), cells with one mutation (type 1), and cells with two mutations (type 2). We define , , and as the number of type 0, type 1, and type 2 cells, respectively, which means that
| (1) |
At some time (assumed to be ), one of the tissue cells gets a first mutation with a rate . Sometime later, a second mutation appears in one of the single-mutated cells with a rate . Note that this might happen before all the tissue cells will have the single mutation, i.e., before the fixation of the first mutation. It is realistic also to assume that the system is in a so-called strong-selection and weak-mutation regime with (3,29, 30, 31). This is because the mutations are rare events due to a very low probability of escaping the DNA repair mechanisms. This also means that the dominating processes that evolve the system are cell divisions and removals that at the same time must also keep the total number of cells in the tissue fixed. We define cell division rates for the normal, single-mutated, and double-mutated cells as b, , and , respectively. The parameter is known as a fitness parameter, and it describes how much faster the single-mutated cells replicate in comparison with the normal cells. It reflects the overall physiological impact of this mutation on cellular metabolism: if , the mutation is disadvantageous, corresponds to a neutral effect, whereas for the mutation is advantageous. Similarly, the parameter is a fitness parameter for double-mutated cells that reflects the cumulative effect of both mutations influencing the cellar metabolic processes (15).
Because the total number of cells in the tissue is constant and equal to N, there are possible discrete states in the system, as shown in Fig. 2 a. Each state can be characterized by just two integer numbers with , which corresponds to the system having cells with one mutation, cells with two mutations, and cells without mutations. For example, the state describes the state with one single-mutated cell, zero cells with two mutations, and normal cells without mutations. The state describes the situation when all cells have the single mutation, i.e., this is the fixation of the first mutation. In the state all cells are double-mutated, and this is the fixation of both mutations, which is also assumed to be the beginning of cancer. In our model, the cancer initiation process starts in the state and ends in the state : see Fig. 2. This is because we are interested in understanding the mutation dynamics in the tissue, and for this purpose one should have at least one cell already mutated. It is also important to note that the transition from the state to the state is irreversible. The reason is that in the state there are no wild-type cells left, and it is now not possible to have processes that would decrease the number of mutated cells in the tissue.
Figure 2.
(a) A schematic view of the two-dimensional state space associated to fixation of two mutations. Sequential fixation pathway is shown with blue dashed lines, and a possible stochastic tunneling is shown with a red dashed line. (b) The corresponding stochastic transition in the system. Each state corresponds to a population with cells of type 1 and cells of type 2. To see this figure in color, go online.
To construct the effective free-energy landscape for the cancer initiation process in the two-hit model, we need to specify the rates of all possible transitions between different states. As shown in Fig. 2 a, there are two types of discrete states in the system depending on the location in the discrete-state stochastic scheme that we might label as bulk and boundary states. It can be shown that the number of bulk states is equal to , and there are six possible stochastic transitions out of each of them (see Fig. 2 b). The horizontal forward transition rate from the state to the state is given by the rate (Fig 2 b). The first term in this rate reflects the possibility of acquiring the first mutation by any of the normal cells ( of those), whereas the second term reflects the cell replication by the mutated cell and the removal of the normal cell. The horizontal backward transition rate from the state to the state is given by , reflecting the cell replication of the normal cell and the removal of the single-mutated cell. Similarly, as shown in Fig. 2 b, the forward vertical transition rate from the state to the state is given by , and the vertical backward transition rate is . In these cases, the changes in the number of double-mutated cells are taking place only via the cell divisions of the double-mutated cells and removal of the normal cells. More complex processes are taking place in diagonal transitions (see Fig. 2 b). The forward diagonal transition rate to go from the state to the state is equal to . Again, the first term reflects the possibility of the single-mutated cells to acquire the second mutation ( single-mutated cells in the system in the starting state), and the second term is due to the cell replication of the double-mutated cell and the removal of the single-mutated cell. Then the backward diagonal transition from the state to the state is given by , which corresponds to the cell replication of the single-mutated cell and the removal of the double-mutated cell. In the supporting material, we explicitly show how to evaluate the transition rates , , and , yielding the following expressions
| (2) |
As one can see from Fig. 2 a, there are also boundary states that lie on the horizontal, vertical, and diagonal axes. They correspond to the situation with (only single- or double-mutated cells, diagonal line) or (only normal or double-mutated cells, vertical line) or (only normal or single-mutated cells, horizontal line). The number of stochastic transitions out of these states varies between 1 and 3, which is less than 6 due to the boundary location, but the specific rates follow the same rules as for the bulk states.
Knowing all the transition rates between different states allows us to evaluate the average residence times in each state. For any bulk state , we have
| (3) |
and similar expressions can be also obtained for the boundary states. This is closely related to our recent study on temporal order of mutations in cancer where we also utilized a free-energy landscape picture to clarify the underlying microscopic processes (15). Then the effective free-energy potential for the system can be estimated via the inverse residence times as
| (4) |
This can be justified by noting that the residence times in each state might be viewed as proportional to the probability for the system to be found in the given state, . The results of our estimates for the effective free-energy landscape are presented in Fig. 3 a. One can see that there is a broad effective free-energy mountain that correspond to the most bulk states surrounded by free-energy valleys that correspond to the boundary states.
Figure 3.
(a) Effective free-energy potential in the space of all possible states (), which is proportional to inverse residence times in each state, . In calculations , , , , and were utilized. (b) Schematic view of the optimal pathways that include only the boundary states. To see this figure in color, go online.
The cancer initiation dynamics in the two-hit model can be investigated by analyzing stochastic transitions in the effective discrete-state scheme presented in Fig. 2 a. There are several ways it can be done. In this work, we employ the method of first-passage probabilities that was already successfully applied in earlier studies of cancer initiation dynamics (14,15). In this approach, one could define functions as the probability to reach the final fixation state at time t given that system starts at state at time . The temporal evolution of these functions is described by a set of following backward master equations,
| (5) |
for the bulk states. Similar, but simpler expressions can be obtained for the boundary states. In addition, we have an initial condition , which means that the fixation is instantaneous if the system already starts in the final state. The first-passage probability functions should provide a full description of cancer initiation process. We are particularly interested in the mean fixation probabilities and the mean fixation times , starting from the state .
This first-passage approach allows us to obtain exact results but only small values of N. In the supporting material, we provide detailed derivations (supported by Monte Carlo computer simulations) for and systems. However, the typical number of tissues cells is much larger, and it ranges from to , but at these conditions, it is not feasible to get explicit solutions. It is possible, however, to investigate the cancer initiation dynamics in the system using Monte Carlo computer simulations, but even this approach is challenging because the total number of states is of the order of .
The analysis of the free-energy landscape presented in Fig. 3 a suggests another strategy to investigate the cancer initiation dynamics. Because the bulk states correspond to an effective maximum, it is reasonable to assume that the number of pathways going via these states will not be large. This suggests that the dominating pathways on the route to the two-mutations fixation must be those that follow only the boundary states. There are two such pathways, as illustrated in Fig. 3 b. Then, instead of trying to account for all possible pathways in the system, the realistic description of the cancer initiation process can be obtained by considering only these two pathways. This significantly simplifies theoretical analysis, and it also allows to understand better the underlying microscopic picture. The main reason for the boundary pathways dominating the fixation dynamics is that there are few transitions out of each of those states, leading to longer residence times on them. This would translate then to the lower effective free energies, which corresponds to boundary pathways being the preferred routes in the mutation fixation in these systems.
The dynamics of cancer initiation in the stochastic model that accounts only for the boundary states (see Fig. 3 b) can be explicitly analyzed as shown in detail in the supporting material. More specifically, the expression for the two-mutations fixation probability starting from the state is given by
| (6) |
where
| (7) |
is the forward transition rate (Fig. 3 b) for the states on the horizontal axis (); and
| (8) |
is the fixation probability starting from the state (one double-mutated cell).
The results of theoretical calculations are presented in Fig. 4 for various sets of parameters. It is found that in the weak mutation limit (), the fixation probability depends strongly on the fitness parameter and weakly on the fitness parameter . This is because in this limit Eq. (6) simplifies into
| (9) |
which is essentially the expression for the fixation of the first mutation. One can easily understand this from the scheme in Fig. 3 b. In the weak mutation limit, the dominating pathway is the horizontal-diagonal path, whereas the vertical path has a very low contribution. In addition, it is enough to reach the state for evaluating the overall fixation probability because the transition to this state is irreversible. These arguments suggest that the overall fixation of two mutations in the model with only boundary states can be well approximated by the fixation of the first mutation.
Figure 4.
(a) Fixation probability for the model with only boundary states as a function of the fitness parameter for different values of the fitness parameter . Note that several curves are on the top of each other, i.e., no dependence on is observed. (b) Mean fixation times for the model with only boundary states as a function of the fitness parameter for different values of the fitness parameter . In calculations, the parameters , , and were utilized. To see this figure in color, go online.
The mean fixation times can also be derived using the same method of calculations as for the fixation probabilities as explained in the supporting material. But it is more instructive to use the following arguments to derive the approximate expression, which also explains better the microscopic processes in the system. Utilizing the previous theoretical analysis (14,15), the mean fixation time for two mutations can be approximated as
| (10) |
where
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
We also have from Eq. (2) that . This expression implies that there are five contributions to the mean fixation time. The first term, , describes the time it takes to move along the horizontal pathway to reach the state , and it corresponds to the mean fixation time of only the first mutation. The second term, , evaluates the average time to move from the horizontal path to the diagonal path. It reflects possible multiple reversible transitions between the state and . The third term, , describes the average time to be on the diagonal path before reaching the full fixation. The fourth term, , is the time to jump from the horizontal path to the vertical path, and it is given by the residence time in the state . Finally, the fifth term, , describes the average time on the vertical path before reaching the fixation. Our approximate expression for the mean fixation times has been tested with Monte Carlo computer simulations (not shown here), and good agreement is found, especially in the most biologically relevant regions of and .
The results of calculations for the mean fixation times in the model with only boundary states are presented in Fig. 4 b. Two different behaviors are observed depending on the value of the fitness parameter . If is close to 1, then the monotonic increase in the overall fixation time as a function of the fitness parameter is predicted (Fig. 4 b). One can understand this by looking into the scheme in Fig. 3 b. The system spends most of the time on the diagonal path. Increasing significantly slows down the motion on this path in the direction of the fixation since the single-mutated cells can replicate faster than the double-mutated cells for . In addition, the motion on the vertical path is also not fast due to . More interesting behavior with a nonmonotonic dependence on is observed for larger values of : see Fig. 4 b. This can be again explained by exploring the stochastic scheme in Fig. 3 b. Although , the slowest step in the overall fixation is a translocation along the horizontal path. Clearly, increasing will decrease this term and accelerate the overall dynamics. However, for the motion along the diagonal path will become slow. These two factors lead to the overall nonmonotonic behavior in the system.
We hypothesize that the cancer initiation process can be well described by analyzing only those pathways that follow the boundary states. Our idea is supported by constructing an effective free-energy landscape (Fig. 3 a). To fully test this proposal, we analyze the dynamics of fixation of two mutations in the full model (with all possible discrete states) and in the model with only boundary states using Monte Carlo computer simulations for realistic sets of parameters. The results are presented in Fig. 5. In order to fairly compare the dynamics of cancer initiation, both models (all states and only boundary states) have been studied only with the computer simulations, although our analytical calculations, as explained above, agree with the computer simulations predictions for the model with only boundary states.
Figure 5.
(a) Fixation probability for the full model versus the model with only boundary states. (b) Mean fixation times for the full model versus the model with only boundary states. Solid lines correspond to the model with only boundary states, and dashed curves describe the full model. In calculations, the parameters , , and were utilized. To see this figure in color, go online.
The comparison of fixation probabilities is presented in Fig. 5 a, showing a very good agreement for all ranges of parameters. Slight deviations between the model with optimal pathways and the full model are observed only near . The advantage of our theoretical picture is that these observations can be explained using the schemes in Figs. 2 a and 3 b. Due to weak mutations rates (), for the system spends a significant amount of time in the horizontal axis of states with . This opens the possibility of stochastic tunneling, i.e., moving to the bulk states and crossing them on the road to the overall fixation. Increasing the fitness parameter moves the system faster to the diagonal axis of states, from which the stochastic tunneling is not possible: see Fig. 3 b.
The mean fixation times for the full model and for the model with only boundary states are presented in Fig. 5 b. Although the deviations in the fixation times are larger than the differences in the fixation probabilities in some regions, the overall agreement is quite satisfactory. The model with the optimal pathways correctly describes the overall trends and quantitatively agrees with the full model for and for large values of this fitness parameter. The difference found at the region around can be explained using the same arguments as above. In this region, the system is originally found mostly on the horizontal axis (see Fig. 3 b), opening the possibilities for exploring the side pathways via the bulk states (stochastic tunneling). But from these pathways the system can escape to the vertical and diagonal axis faster than in the optimal-pathway model. This explains why the mean fixation times in the model with the boundary states in the region around are larger than the mean fixation times in the full model.
Discussion
Although there are some deviations between the predictions of the optimal-pathway model and the full model of two-mutations fixation, it can be argued that a very simple theoretical picture based on utilizing the effective free-energy landscape is capturing many features in the cancer initiation dynamics. Importantly, it allows to significantly simplify the analysis of the complex processes associated with the tumor formation. Instead of looking at a very large number of possible pathways on the road to fixation (visiting ∼ states), one might concentrate on the processes that are going via very few pathways (visiting ∼ states). This allows us to obtain analytical estimates that significantly improve our understanding of the microscopic mechanisms of underlying processes. For example, the order of mutations (15) and the role of the fitness parameters now can be explained much better.
This theoretical approach can be easily generalized to the system with more than two mutations. If the tumor appears after the fixation of M mutations, then the overall number of states in the system will be ∼, and it will be prohibitively difficult to analyze such systems even with the most advanced computational tools. Our method suggests that, instead, one could mostly account only for ∼ boundary states. One could visualize these processes by noting that the overall space of discrete states is occupying the diagonally cut half of the M-dimensional cube, and the boundary states correspond to the surfaces surrounding this figure. Furthermore, our theoretical results suggest that in the cancer initiation processes, the dominating pathways are those that are less heterogeneous from the point of view of different types of cells. In other words, in the system with M mutations, there are types of cells that might exist simultaneously (where the number of mutations range from zero to M), and we predict that the road to fixation follows mostly via the states with the smaller number of types of cells. From a microscopic point of view, from the more heterogeneous states there are more ways of escaping to less heterogeneous states. This is another way of looking at the effective free-energy landscape of the cancer initiation process.
Another advantage of the proposed theoretical method is that it can be sequentially improved by again using the effective free-energy landscape in Fig. 3 a. To make the description of the dynamic properties of the fixation process more precise, one might add a few more states to the boundary states. These additional states lie near the corners of the stochastic scheme in Fig. 3 a. It is expected that this will make the predictions for the fixation probabilities and mean fixation times much closer to the exact values. But importantly, this should not significantly complicate the calculations of dynamic properties.
Although our theoretical approach successfully captures the main physical features of the cancer initiation process with multiple mutations, it is important to discuss its limitations and future directions. Because before the formation of the tumor the total number of tissue cells is constant, the cell replications must be accompanied by cell deaths. Following the typical procedure adopted in the field (3), we utilized the Moran process, which is a mathematical procedure that allows to keep the total number of cells in the system fixed by following specific rules. This procedure assumes that after one cell divides, any other cell in the system can be instantly removed with the same probability, which effectively neglects the spatial structure of the tissue. But taking into account the tissue structure, for example, by utilizing the Moran process on graphs (32), might lead to very complex dynamic phenomena. This direction will be interesting to explore. However, there might be a more general problem since the exact biochemical mechanisms of how the normal tissue is regulating cell replications and deaths are still not well understood (2). In other words, the use of the Moran process might not be a reasonable approach, potentially leading to some artifacts in the theoretical analysis of the cancer initiation dynamics. One of the possible future directions is also to explore more mechanical approaches that utilize various ideas from chemistry and physics in clarifying the cell replications and cell deaths processes (33). In addition, our theoretical approach did not distinguish the cells with the same number of mutations but different types of mutations. However, it is known that interactions between different subclones might be crucial during the cancer progression. At the same time, the proposed theoretical method can be extended in this direction. It will be important to explore various theoretical and experimental tools for more quantitative investigations of cancer initiation processes.
Author contributions
H.T. and A.B.K. designed the research. H.T. and C.S carried out the research. H.T. and A.B.K. wrote the article.
Acknowledgments
We acknowledge the support from the Welch Foundation (C-1559), from the NSF (CHE-1953453 and MCB-1941106), and from the Center for Theoretical Biological Physics sponsored by the NSF (PHY-2019745).
Declaration of interests
The authors declare no competing interests.
Editor: Alemayehu A. Gorfe.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2022.05.011.
Supporting material
References
- 1.Weinberg R.A. Garland Science; 2013. The Biology of Cancer. [Google Scholar]
- 2.Lodish H., Berk A., et al. Matsudaira P. Macmillan; 2008. Molecular Cell Biology. [Google Scholar]
- 3.Nowak M.A. Harvard University Press; 2006. Evolutionary Dynamics: Exploring the Equations of Life. [Google Scholar]
- 4.Hanahan D., Weinberg R.A. The hallmarks of cancer. Cell. 2000;100:57–70. doi: 10.1016/s0092-8674(00)81683-9. [DOI] [PubMed] [Google Scholar]
- 5.Tomasetti C., Vogelstein B. Cancer etiology. Variation in cancer risk among tissues can be explained by the number of stem cell divisions. Science. 2015;347:78–81. doi: 10.1126/science.1260825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tomasetti C., Li L., Vogelstein B. Stem cell divisions, somatic mutations, cancer etiology, and cancer prevention. Science. 2017;355:1330–1334. doi: 10.1126/science.aaf9011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hanahan D., Weinberg R.A. Hallmarks of cancer: the next generation. Cell. 2011;144:646–674. doi: 10.1016/j.cell.2011.02.013. [DOI] [PubMed] [Google Scholar]
- 8.Dominik W., Natalia K. World Scientific; 2014. Dynamics of Cancer: Mathematical Foundations of Oncology. [Google Scholar]
- 9.Lahouel K., Younes L., et al. Tomasetti C. Revisiting the tumorigenesis timeline with a data-driven generative model. Proc. Natl. Acad. Sci. U S A. 2020;117:857–864. doi: 10.1073/pnas.1914589117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Komarova N.L., Sengupta A., Nowak M.A. Mutation–selection networks of cancer initiation: tumor suppressor genes and chromosomal instability. J. Theor. Biol. 2003;223:433–450. doi: 10.1016/s0022-5193(03)00120-6. [DOI] [PubMed] [Google Scholar]
- 11.Iwasa Y., Michor F., Nowak M.A. Stochastic tunnels in evolutionary dynamics. Genetics. 2004;166:1571–1579. doi: 10.1534/genetics.166.3.1571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Foo J., Leder K., Michor F. Stochastic dynamics of cancer initiation. Phys. Biol. 2011;8:015002. doi: 10.1088/1478-3975/8/1/015002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Paterson C., Clevers H., Bozic I. Mathematical model of colorectal cancer initiation. Proc. Natl. Acad. Sci. U S A. 2020;117:20681–20688. doi: 10.1073/pnas.2003771117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Teimouri H., Kochugaeva M.P., Kolomeisky A.B. Elucidating the correlations between cancer initiation times and lifetime cancer risks. Sci. Rep. 2019;9:18940–18948. doi: 10.1038/s41598-019-55300-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Teimouri H., Kolomeisky A.B. Temporal order of mutations influences cancer initiation dynamics. Phys. Biol. 2021;18 doi: 10.1088/1478-3975/ac0b7e. [DOI] [PubMed] [Google Scholar]
- 16.Haeno H., Maruvka Y.E., et al. Michor F. Stochastic tunneling of two mutations in a population of cancer cells. PLoS One. 2013;8:e65724. doi: 10.1371/journal.pone.0065724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ashcroft P., Michor F., Galla T. Stochastic tunneling and metastable states during the somatic evolution of cancer. Genetics. 2015;199:1213–1228. doi: 10.1534/genetics.114.171553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Proulx S.R. The rate of multi-step evolution in Moran and Wright–Fisher populations. Theor. Popul. Biol. 2011;80:197–207. doi: 10.1016/j.tpb.2011.07.003. [DOI] [PubMed] [Google Scholar]
- 19.Weinreich D.M., Chao L. Rapid evolutionary escape by large populations from local fitness peaks is likely in nature. Evolution. 2005;59:1175–1182. [PubMed] [Google Scholar]
- 20.Weissman D.B., Desai M.M., et al. Feldman M.W. The rate at which asexual populations cross fitness valleys. Theor. Popul. Biol. 2009;75:286–300. doi: 10.1016/j.tpb.2009.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Guo Y., Vucelja M., Amir A. Stochastic tunneling across fitness valleys can give rise to a logarithmic long-term fitness trajectory. Sci. Adv. 2019;5:eaav3842. doi: 10.1126/sciadv.aav3842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tang E., Agudo-Canalejo J., Golestanian R. Topology protects chiral edge currents in stochastic systems. Phys. Rev. X. 2021;11:031015. [Google Scholar]
- 23.Sherr C.J. Principles of tumor suppression. Cell. 2004;116:235–246. doi: 10.1016/s0092-8674(03)01075-4. [DOI] [PubMed] [Google Scholar]
- 24.Kolomeisky A.B. CRC Press; 2015. Motor Proteins and Molecular Motors. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Phillips R., Kondev J., et al. Orme N. Garland Science; 2012. Physical Biology of the Cell. [Google Scholar]
- 26.Knudson A.G. Mutation and cancer: statistical study of retinoblastoma. Proc. Natl. Acad. Sci. U S A. 1971;68:820–823. doi: 10.1073/pnas.68.4.820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Knudson A.G. Two genetic hits (more or less) to cancer. Nat. Rev. Cancer. 2001;1:157–162. doi: 10.1038/35101031. [DOI] [PubMed] [Google Scholar]
- 28.Nowak M.A., Komarova N.L., et al. Lengauer C. The role of chromosomal instability in tumor initiation. Proc. Natl. Acad. Sci. U S A. 2002;99:16226–16231. doi: 10.1073/pnas.202617399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lynch M. Rate, molecular spectrum, and consequences of human mutation. Proc. Natl. Acad. Sci. U S A. 2010;107:961–968. doi: 10.1073/pnas.0912629107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Orr H.A. The genetic theory of adaptation: a brief history. Nat. Rev. Genet. 2005;6:119–127. doi: 10.1038/nrg1523. [DOI] [PubMed] [Google Scholar]
- 31.Gillespie J.H. Molecular evolution over the mutational landscape. Evolution. 1984;38:1116–1129. doi: 10.1111/j.1558-5646.1984.tb00380.x. [DOI] [PubMed] [Google Scholar]
- 32.Lieberman E., Hauert C., Nowak M.A. Evolutionary dynamics on graphs. Nature. 2005;433:312–316. doi: 10.1038/nature03204. [DOI] [PubMed] [Google Scholar]
- 33.Sinha S., Malmi-Kakkada A.N., et al. Thirumalai D. Spatially heterogeneous dynamics of cells in a growing tumor spheroid: comparison between theory and experiments. Soft Matter. 2020;16:5294–5304. doi: 10.1039/c9sm02277e. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.