Visual Field Prediction

Abstract

Purpose

Two novel deep learning methods using a convolutional neural network (CNN) and a recurrent neural network (RNN) have recently been developed to forecast future visual fields (VFs). Although the original evaluations of these models focused on overall accuracy, it was not assessed whether they can accurately identify patients with progressive glaucomatous vision loss to aid clinicians in preventing further decline. We evaluated these 2 prediction models for potential biases in overestimating or underestimating VF changes over time.

Design

Retrospective observational cohort study.

Participants

All available and reliable Swedish Interactive Thresholding Algorithm Standard 24-2 VFs from Massachusetts Eye and Ear Glaucoma Service collected between 1999 and 2020 were extracted. Because of the methods’ respective needs, the CNN data set included 54 373 samples from 7472 patients, and the RNN data set included 24 430 samples from 1809 patients.

Methods

The CNN and RNN methods were reimplemented. A fivefold cross-validation procedure was performed on each model, and pointwise mean absolute error (PMAE) was used to measure prediction accuracy. Test data were stratified into categories based on the severity of VF progression to investigate the models’ performances on predicting worsening cases. The models were additionally compared with a no-change model that uses the baseline VF (for the CNN) and the last-observed VF (for the RNN) for its prediction.

Main Outcome Measures

PMAE in predictions.

Results

The overall PMAE 95% confidence intervals were 2.21 to 2.24 decibels (dB) for the CNN and 2.56 to 2.61 dB for the RNN, which were close to the original studies’ reported values. However, both models exhibited large errors in identifying patients with worsening VFs and often failed to outperform the no-change model. Pointwise mean absolute error values were higher in patients with greater changes in mean sensitivity (for the CNN) and mean total deviation (for the RNN) between baseline and follow-up VFs.

Conclusions

Although our evaluation confirms the low overall PMAEs reported in the original studies, our findings also reveal that both models severely underpredict worsening of VF loss. Because the accurate detection and projection of glaucomatous VF decline is crucial in ophthalmic clinical practice, we recommend that this consideration is explicitly taken into account when developing and evaluating future deep learning models.

Detecting and monitoring disease worsening are imperative to managing glaucoma and preserving vision in patients. As the leading cause of irreversible blindness worldwide,¹ glaucoma necessitates close longitudinal monitoring by clinicians to inform timely medical and surgical interventions to lower intraocular pressure. In particular, analysis of standard automated perimetry visual field (VF) tests remains a cornerstone in evaluating functional deterioration and estimating future visual defects in glaucoma suspects and patients.²

Among the number of analytical methods available to assess changes in VFs, trend-based analyses are commonly used in clinical practice to calculate the rate of change over time of global indices, such as mean deviation (MD) and VF index. Pointwise linear and nonlinear regression approaches have also been developed.³ However, these existing methods are significantly limited in terms of sensitivity, accuracy, and feasibility. For instance, regression of global indices often misses localized VF changes,⁴ and many models assume constant additive or multiplicative rates of progression that do not reflect the true nature of the disease course.⁵ Furthermore, VF testing itself has variability in both the short-term and long-term, meaning that a large number of VF tests are required to achieve clinically and statistically meaningful predictions.⁶

Recent applications of artificial intelligence, including its subfields of machine learning and deep learning (DL), show promise to improve clinical practice in ophthalmology. Deep learning methods have enabled much of this progress by eliminating the need for manual feature engineering.⁷ Although most of these DL applications have focused on the diagnosis and classification of ophthalmic diseases, a few researchers have ventured into the development of predictive models. Notably, 2 recent studies in glaucoma research by Wen et al⁸ and Park et al⁹ used novel DL algorithms to predict future VF examinations. Wen et al⁸ developed a convolutional neural network (CNN) that is able to predict VFs in glaucomatous eyes up to 5.5 years in the future, using only a single VF as input. Park et al⁹ built a recurrent neural network (RNN) that receives a series of 5 consecutive VF inputs to predict the sixth VF as its output. The CNN and RNN models predict pointwise raw decibel (dB) sensitivities and total deviation (TD) values, respectively.

Although both DL models reported improved predictive accuracy compared with previously established methods, their potential for clinical translation has been insufficiently explored. A major question remains whether these models are clinically valuable in predicting worsening cases of VFs in progressive glaucoma patients. In this study, we reimplemented DL models described by Wen et al⁸ and Park et al⁹ using an independent, large longitudinal data set to investigate their real-world potential to aid clinicians in glaucoma management.

Methods

This study was approved by the Institutional Review Board of Massachusetts Eye and Ear (Boston, MA) and was performed in accordance with all tenets of the Declaration of Helsinki. The Institutional Review Board waived the need for informed consent because of the retrospective nature of the study.

Swedish Interactive Thresholding Algorithm Standard 24-2 VFs (Humphrey Field Analyzer, Carl Zeiss Meditec, Inc) taken by patients between the years of 1999 and 2020 at Massachusetts Eye and Ear Glaucoma Service were obtained from available medical records and deidentified. Visual field examinations with false-positive rate > 30%, false-negative rate > 30%, and/or fixation losses > 30% were considered unreliable and excluded from the study. We also extracted age, sex, and the eye tested from the VFs. A total of 90 684 VFs from 21 120 patients remained for analysis (Table 1).

Table 1.

Demographic Characteristics of the Overall Institutional Data Set

Demographics	Value
Samples (n)	90 684
Subjects (n)	21 120
Eye
Right (n)	18 965
Left (n)	18 526
Sex
Male (n)	9275
Female (n)	11 845
Mean age (yrs), mean ± SD	62.94 ± 15.07
MD (dB), mean ± SD	−3.95 ± 5.66

dB = decibel; MD = visual field mean deviation; SD = standard deviation.

All DL was performed with the open-source machine learning platform Tensorflow (version 2.4.0, https://www.tensorflow.org) and its embedded Keras module. A Dell PC with Intel Core-i7 CPU, 64 GB memory, and NVIDIA RTX 2080 GPU, 6 GB memory, were used. Our reimplementation codes are shared publicly at https://github.com/mohaEs/VFPrediction.

Method #1: Via CNN

A simplified version of the CNN model proposed by Wen et al⁸ (MWen) was reimplemented. Because the method uses pairs of input-output VFs, we combined extracted VFs into all possible pairings for each patient based on the time elapsed between tests. Patients with only 1 VF were excluded. Similar to the original paper, we binned the remaining VF pairs into 5 prediction time points of 0.5-year intervals: 0.75 to 1.25 years (1-year prediction time point), 1.75 to 2.25 (2 years), 2.75 to 3.25 (3 years), 3.75 to 4.25 (4 years), and 4.75 to 5.25 (5 years). Any VF pairs that were < 0.75 year, > 5.25 years, or not included in the specified time point intervals were also excluded. The resulting data set for evaluating the MWen method included 54 373 VF pairs from 7472 patients.

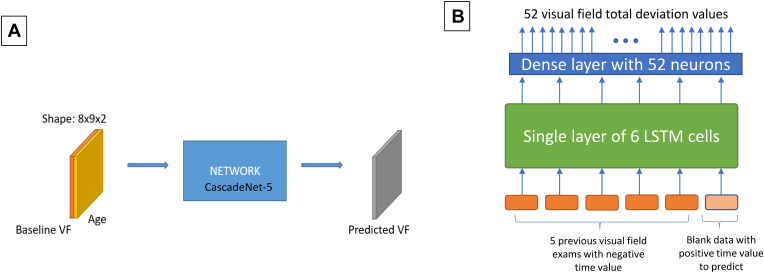
We used the best-performing model architecture identified in the original paper, CascadeNet-5, for our reimplementation. Because Wen et al⁸ reported that using age as an additional input feature into the DL model resulted in a statistically superior performance (P = 0.0003, paired Wilcoxon rank sum test), we also included age as a clinical predictor. The CNN model received single VFs appended with patient age as input in the form of 2 × 8 × 9 tensors; the first 8 × 9 array encoded the perimetry sensitivity values from the VF, and the second 8 × 9 array encoded age as a continuous value in all cells. A single 8 × 9 tensor representing the predicted target VF was produced as output by the model. Figure 1A shows the input/output structure of the reimplemented MWen model. Full details of this method are described in the original paper.⁸

Figure 1.

Simplified illustrations of the MWen (A) and MPark (B) methods. LSTM = long short-term memory; MPark = recurrent neural network method from Park et al; MWen = convolutional neural network method from Wen et al; VF = visual field.

Method #2: Via RNN

Because the RNN model proposed by Park et al⁹ requires 6 consecutive VFs (5 for input and 1 for the prediction’s ground truth), we excluded subjects with < 6 VFs for the reimplementation (MPark). If a patient had > 6 VFs, we supplied multiple VF series as input data elements for the neural network while preserving consecutive order of the tests. This was achieved by moving the time window 1 step forward until all input data were used. For example, if a patient had 7 total consecutive VFs, 2 series were possible: VFs #1 to 6 and #2 to 7. In total, 24 430 VF series from 1809 patients qualified to be used in this method.

An RNN algorithm called long short-term memory¹⁰ was used for this approach, and the specific neural network architecture and methods are described in detail in the original paper.⁹ Figure 1B shows the structure of the proposed method in Park et al.⁹ In brief, 5 previous VFs along with 1 special input that specified the intended prediction date were provided to a single layer of 6 long short-term memory cells. Each VF consisted of 52 TD values, 52 pattern deviation values, reliability data, and time displacement values (number of days from the most recent VF). Only 52 out of 54 total points from each VF were used, excluding the 2 points occupied by the physiologic blind spot. A single-layer fully connected network (dense layer) consisting of 52 neurons produced a final output of 52 TD values with each neuron in the dense layer generating 1 VF test point for the prediction.

Park et al⁹ did not share the hyperparameters of their final DL model. Therefore, we used the best 17 hyperparameters, including regularizers, initializers, activation functions, dropout rate, type of optimizer, and learning rate, by searching through 2000 trials over 10% of the training data set using the Hyperband tuning procedure.^11,12

Evaluation Scheme

A fivefold cross-validation procedure was performed on the models using their respective data sets. For each session of cross-validation, we first separated VFs at the patient level into 2 parts: 80% for the training set and the remaining 20% for the test set. Table 2 shows the details of the train/test data allocations at each prediction time point. Furthermore, we allocated 10% of each training set for validation to monitor loss values and to prevent overfitting of the models. Training was stopped if loss of the validation set made no improvement with 50 epochs of patience. To optimize the networks, we used a stochastic gradient descent optimization algorithm called Adam¹³ with a learning rate of 1 × 10⁻³.

Table 2.

Train/Test Split of the MWen Data Set with Respect to Prediction Time Points

	1 Year	2 Years	3 Years	4 Years	5 Years
Subjects (n), train/test	≈4752/1188	≈3364/841	≈2589/648	≈2088/522	≈1666/417
Observations (n), train/test	≈15 596/3867	≈10 122/2678	≈7595/1777	≈5743/1355	≈4414/1146

MWen = convolutional neural network method from Wen et al.

Pointwise mean absolute error (PMAE) was used as the main accuracy metric of the models’ predictions. We compared the models’ PMAEs to those achieved by a no-change model, which assume that VFs remain the same over time. Therefore, the predicted VF produced by the no-change model is the same as the baseline VF for MWen or the same as the last-observed (fifth) VF for MPark. The CNN method from Wen et al was also compared with a simulated model introduced in Wen et al⁸ based on the mean (−0.36 dB/year) and standard deviation (0.60 dB/year) of the rate of progression (ROP) from the Early Manifest Glaucoma Trial.¹⁴

To further investigate prediction performance, we also stratified the test data into different categories based on the severity of VF progression. The procedures used to stratify the VFs differed between the models because of the nature of their methods. For the MWen algorithm that uses only 1 input VF, we partitioned the MWen test data based on changes in MD between baseline (the input VF) and follow-up (the ground truth, or target prediction, VF) at each prediction time point (categories: ΔMD ≥ −3 dB, −6 dB < ΔMD < −3 dB, ΔMD ≤ −6 dB). For instance, a VF pair with ΔMD = −4 dB meant that the ground truth VF’s MD was 4 dB lower than the input VF’s MD and would fall into the second category.

For the MPark algorithm, we used 4 progression analysis methods from the literature that similarly require consequent VFs to partition the test data into “stable” and “worsening” categories. By selecting these methods, we aimed to represent some of the major approaches to analyzing VF progression: event-based, trend-based, and a combination of both types. Details of the methods can be found in the original papers but are summarized here for reference. For event-based methods, we implemented approaches from Rabiolo et al¹⁵ and Schell et al.¹⁶ The approach of Rabiolo et al¹⁵ is based on the Advanced Glaucoma Intervention Study. In this method, TD values and local pattern arrangements are taken into account to assign a severity score to each VF, and progression is defined as an increase in score of ≥ 4 from the baseline VF for ≥ 3 consecutive tests. Similarly, in the study by Schell et al,¹⁶ progression is defined as a loss of ≥ 3 dB in MD from the baseline MD with this loss confirmed on a subsequent VF test. As for a trend-based method, we used the approach described in the study by Aptel et al¹⁷ that defines worsening as a significantly (P < 0.05) negative VF index slope. Lastly, we selected the method described by Nouri-Mahdavi et al¹⁸ based on pointwise linear regression that incorporates both event- and trend-based features. In this approach, test locations that demonstrate a slope of ≤ −1.0 dB/year with P ≤ 0.01 are considered to be significantly declining, and overall worsening is defined as the number of declining locations exceeding the number of improving locations by ≥ 3.

Finally, we binned the training data into 6 categories based on baseline MD and changes in MD (Table 3) to analyze the composition of our data sets. Oversampling and undersampling methods were then performed on the training data to achieve more balanced data set compositions. In the oversampling method, we randomly duplicated VFs in the classes with the lowest number of samples to approximately match the number of VFs in the classes with the greatest number of samples. In the undersampling method, we randomly deleted VFs in the majority classes instead to approximately equal the number of VFs in the minority classes. The models were retrained on the newly balanced data sets and retested to investigate the effect of balanced training data on prediction accuracy.

Table 3.

Categories of Visual Field Progression Status for Oversampling and Undersampling Methods

	Category I	Category II	Category III	Category IV	Category V	Category VI
Definition	−3 < MD0 −3 ≤ ΔMD	−3 < MD0 −6 < ΔMD < −3	−3 < MD0 ΔMD ≤ −6	−3 ≥ MD0 −3 ≤ ΔMD	−3 ≥ MD0 −6 < ΔMD < −3	−3 ≥ MD0 ΔMD ≤ −6
Interpretation	Healthy stable	Healthy with mild worsening	Healthy with severe worsening (converting)	Stable patient	Patient with mild worsening	Patient with severe worsening

ΔMD = change in mean deviation; MD₀ = baseline visual field mean deviation.

Statistical Analysis

For each DL algorithm, paired t tests were used to evaluate a significant difference in PMAE between models. We performed all statistical analyses using Python (version 3.8.8, https://www.python.org) and its scientific computation library SciPy (version 1.7.3, https://www.scipy.org).

Results

A total of 90 684 Swedish Interactive Thresholding Algorithm Standard 24-2 Humphrey VF tests from 21 120 patients were extracted from 1999 to 2020, resulting in 54 373 input-output pairs used in MWen and 24 430 series of 6 consecutive VFs used in MPark. In the MWen data set, patients’ mean age was 64.06 ± 13.50 years, and their mean baseline VF MD was −2.74 ± 4.54 dB. In the MPark data set, the mean age of patients was 62.64 ± 11.53 years, and their mean baseline MD was −1.94 ± 3.49 dB. On average, the sixth VF (the VF to be predicted by the RNN model) was 1.17 ± 0.70 years after the final input VF.

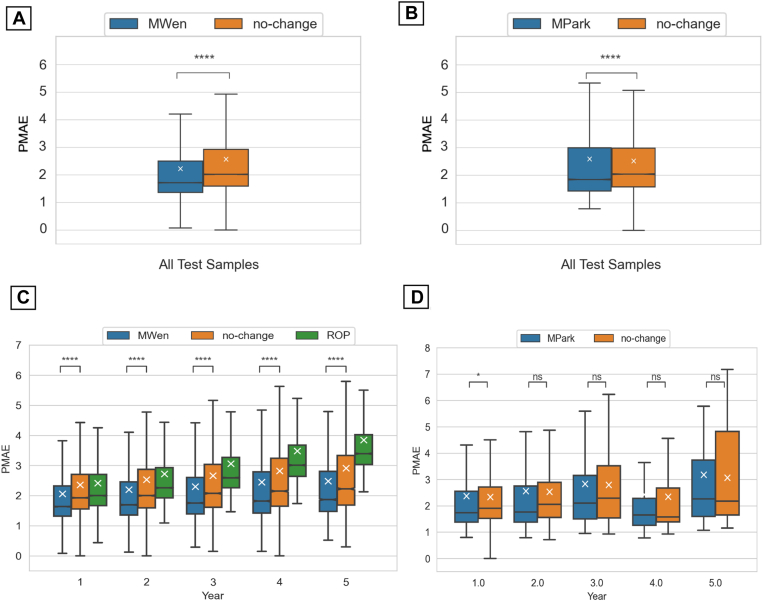
Boxplots of the overall PMAEs achieved by the methods over all of the test samples are shown in Figure 2A, B. Both MWen (PMAE 95% confidence interval [CI]: 2.21–2.24) and MPark (PMAE 95% CI: 2.56–2.61) were statistically better (P < 0.0001) than the no-change model (PMAE 95% CIs: 2.55–2.58 and 2.49–2.53 for MWen and MPark, respectively). When analyzed by prediction time points, MWen also demonstrated statistically significant improvements in prediction accuracies compared with the no-change and ROP models at all 5 time points (P < 0.0001, Fig 2C). In contrast, MPark demonstrated only a small but statistically significant decrease in PMAE at year 1 (0.01 < P ≤ 0.05, Fig 2D) and did not show any significance at years 2 to 5 in comparison to the no-change model.

Figure 2.

Boxplots of pointwise mean absolute error (PMAE) achieved by the models. (A) The accuracy of MWen over all test samples and (C) with respect to prediction time points. (B) The accuracy of MPark over all test samples and (D) with respect to prediction time points. ^∗0.01 < P ≤ 0.05; ^∗∗∗∗P ≤ 0.0001. MPark = recurrent neural network method from Park et al; MWen = convolutional neural network method from Wen et al; ns = not significant; ROP = rate of progression.

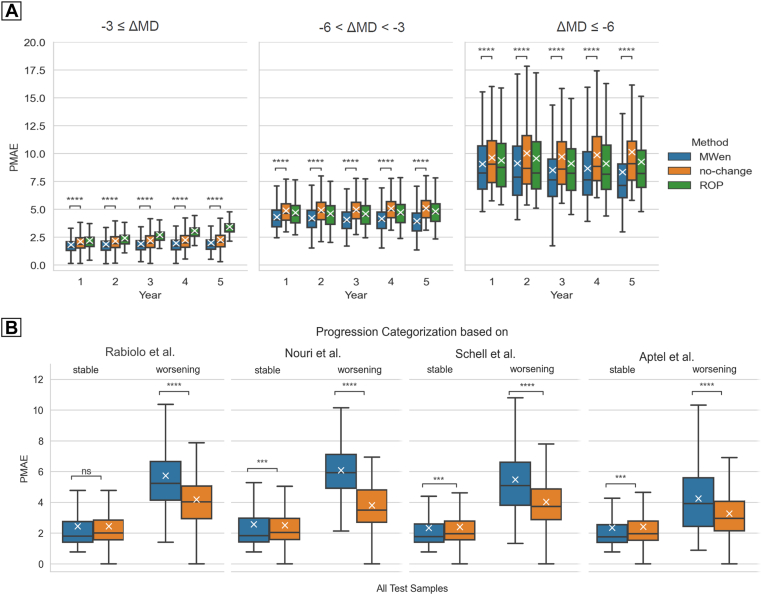
The prediction accuracies of MWen partitioned based on changes in MD and with respect to time points are shown in Figure 3A. Although MWen continued to demonstrate statistically significant improvements in PMAEs (P < 0.001 for all ΔMD categories at all time points), the model’s accuracy greatly decreased when dealing with more severe and worsening cases. For the most stable category (ΔMD better than −3 dB), the average PMAE across all time points for MWen was 1.91, whereas it was 4.13 for the middle category (ΔMD worse than −3 dB but better than −6 dB) and 8.74 for the most severe category (ΔMD worse than −6 dB). Representative examples of VF predictions produced by MWen are shown in Figure 4, and the VFs shown in Figure 4G, H demonstrate how the model can completely miss severe altitudinal VF defects in its predictions.

Figure 3.

Boxplots of pointwise mean absolute error (PMAE) achieved by the models, stratified based on the severity of visual field progression. A, The accuracy of MWen over the test set with respect to prediction time points and partitioned based on changes in MD (ΔMD = MD_truthtarget − MD_baseline). B, The accuracy of MPark over the test set and partitioned based on progression analyzed by the methods of Rabiolo et al, Nouri et al, Schell et al, and Aptel et al. ^∗∗∗0.0001 < P ≤ 0.001; ^∗∗∗∗P ≤ 0.0001. MD = mean deviation; MPark = recurrent neural network method from Park et al; MWen = convolutional neural network method from Wen et al; ns = not significant; ROP = rate of progression.

Figure 4.

Eight random representative examples of visual field predictions from MWen. (A–D) are more stable samples, and (E–H) are worsening samples. MWen = convolutional neural network method from Wen et al; PMAE = pointwise mean absolute error.

As for MPark, the model’s overall PMAEs categorized by stable versus worsening cases are shown in Figure 3B. In comparison to the no-change model, MPark showed statistically significant increases in prediction accuracy on stable cases (0.0001 < P ≤ 0.001) when the progression analysis methods of Nouri et al,¹⁸ Schell et al,¹⁶ and Aptel et al¹⁷ were used to categorize VFs; however, there was no improvement in PMAE when Rabiolo et al¹⁵ was used. Notably, MPark performed statistically worse than the no-change model in terms of PMAE for cases categorized as worsening across all 4 progression analysis methods (P ≤ 0.0001). Representative examples of VF predictions produced by MPark are shown in Figure 5. The subfigure Figure 5E shows an example in which the model entirely missed a glaucomatous VF defect.

Figure 5.

Six random representative examples of visual field predictions from MPark. (A–C) are more stable samples, and (D–F) are worsening samples. MPark = recurrent neural network method from Park et al; PMAE = pointwise mean absolute error.

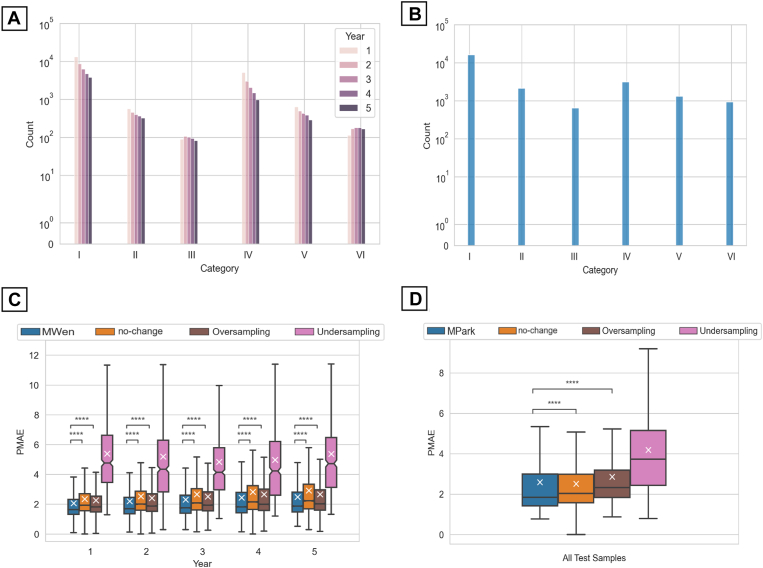
Binning the training data into 6 categories (Table 3) revealed that the training data sets were highly imbalanced in favor of stable cases. Figure 6A, B shows the overall breakdown of data per category. For both models’ data sets, the greatest number of samples was in category I (healthy and stable individuals), whereas the least number of samples was in category III (healthy individuals with severe worsening, i.e., converting to patients). Mean PMAEs resulting from subsequent oversampling and undersampling training methods are summarized in Table 4 and Figure 6C for MWen and Table 5 and Figure 6D for MPark. For MWen, oversampling produced slightly improved PMAEs in comparison to the no-change model; however, oversampling PMAEs were still statistically worse than the original PMAEs across all prediction time points. Undersampling resulted in statistically lower accuracy for MWen with mean PMAEs that were around 2 times greater than the original PMAEs. A similar trend was observed for MPark: the 2 data balancing methods did not result in increased prediction accuracy. Oversampling produced statistically worse PMAEs at years 1 to 4 but did not show a statistical difference at year 5. Undersampling consistently demonstrated statistically higher PMAEs that ranged from approximately 4 to 6 dB.

Figure 6.

Distributions of the (A) MWen and (B) MPark training data sets with respect to progression categories (I–VI), and boxplots of pointwise mean absolute error (PMAE) regarding sampling strategies for (C) MWen and (D) MPark. The prediction intervals for MPark are arbitrary and not limited to the 5 prediction time points like MWen. ^∗∗∗∗P ≤ 0.0001. MPark = recurrent neural network method from Park et al; MWen = convolutional neural network method from Wen et al.

Table 4.

Comparison of Mean PMAE between MWen Methods and the No-Change and ROP Models

	Year 1	Year 2	Year 3	Year 4	Year 5
No-change	2.35 ± 0.019	2.53 ± 0.029	2.66 ± 0.036	2.82 ± 0.046	2.91 ± 0.056
ROP	2.41 ± 0.018	2.72 ± 0.027	3.05 ± 0.031	3.48 ± 0.038	3.85 ± 0.043
MWen	2.05 ± 0.0184	2.20 ± 0.027	2.30 ± 0.033	2.44 ± 0.042	2.48 ± 0.049
MWen (oversampling)	2.29 ± 0.0196	2.43 ± 0.028	2.53 ± 0.035	2.67 ± 0.044	2.70 ± 0.051
MWen (undersampling)	5.38 ± 0.238	5.19 ± 0.265	4.83 ± 0.236	4.97 ± 0.262	5.37 ± 0.297

MWen = convolutional neural network method from Wen et al; PMAE = pointwise mean absolute error; ROP = rate of progression.

Table 5.

Comparison of Mean PMAE between MPark Methods and the No-Change Model

	Year 1	Year 2	Year 3	Year 4	Year 5
No-change	2.33 ± 0.027	2.52 ± 0.071	2.79 ± 0.222	2.34 ± 0.292	3.06 ± 0.650
MPark	2.37 ± 0.036	2.55 ± 0.112	2.82 ± 0.252	2.42 ± 0.358	3.17 ± 0.844
MPark (oversampling)	2.68 ± 0.032	2.85 ± 0.102	3.10 ± 0.229	2.85 ± 0.322	3.27 ± 0.802
MPark (undersampling)	3.98 ± 0.142	4.38 ± 0.333	4.29 ± 0.941	6.24 ± 1.590	5.97 ± 2.280

MPark = recurrent neural network method from Park et al; PMAE = pointwise mean absolute error.

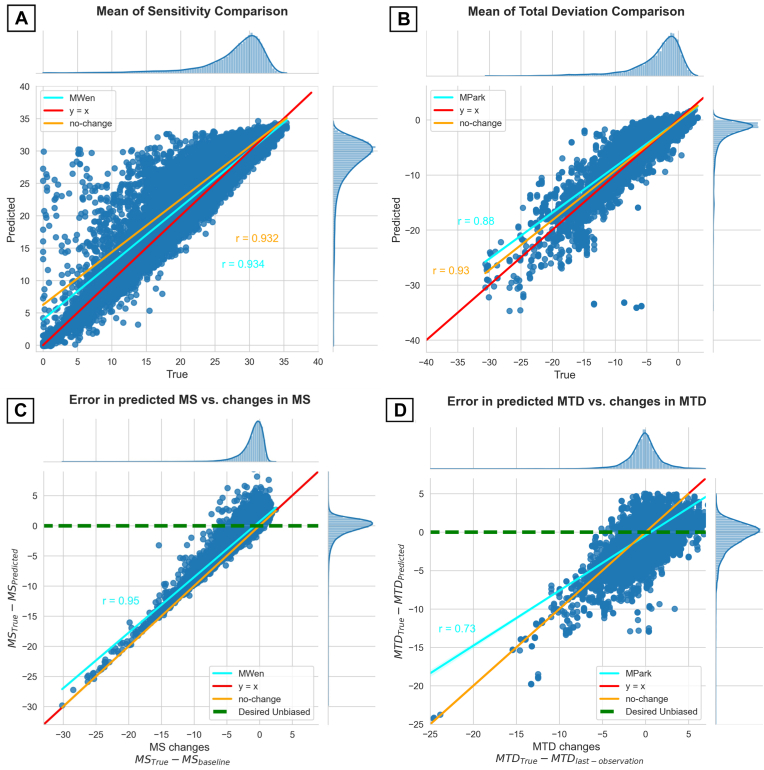
Scatterplots of MWen’s and MPark’s test results regarding mean sensitivity and mean TD values are shown in Figure 7. Although Figure 7A, B shows that both methods’ predictions were generally spread close to the line y = x, which represents ideal predictions without any errors, Figure 7C, D reveals that both methods were highly inaccurate in forecasting worsening VFs: As changes in mean sensitivity and mean TD increased, the models’ predictions strayed farther from the horizontal y = 0 line that signifies the ideal performance of hypothetical unbiased models.

Figure 7.

Scatterplots of prediction results for MWen (left column) and MPark (right column) regarding mean sensitivity (MS) and mean total deviation (MTD) values. (A, B) show the predicted vs. true, targeted values. (C, D) show the error in prediction vs. actual measured change. Although both methods’ predicted values are spread close to y = x (predicted = ground truth) in the top row, the bottom row shows that both methods have significant inaccuracy in forecasting worsening cases; the ideal unbiased prediction model should be near the green dashed line. MPark = recurrent neural network method from Park et al; MWen = convolutional neural network method from Wen et al.

Discussion

The primary aims of this study were to reimplement 2 previously published DL models from Wen et al⁸ and Park et al⁹ that predict pointwise VF examinations and to evaluate the models’ abilities in predicting VF loss using an independent patient population. Our evaluation of the models (PMAE 95% CI: MWen, 2.21–2.24; MPark, 2.56–2.61) confirms the low overall PMAEs reported in the original studies. However, deeper analysis of the models’ performances revealed that both algorithms greatly underpredicted worsening of VF loss. Our results therefore suggest that MWen and MPark have limited clinical applicability because they are insufficient to identify and predict which patients will experience significant VF decline over time.

As detecting worsening of functional defects is the major motivation underlying clinical VF testing, it is important to consider this aspect when evaluating DL models. In clinical practice, the vast majority of treated eyes are stable over long periods of time, whereas only a small but significant subset (3%–17%) may be subject to worsening.¹⁹ Because of this common imbalance of VF data, a progression model’s overall error may be low even if the model underestimates VF changes over time and fails to accurately predict VF loss. For example, Dixit et al²⁰ reported a high accuracy but low diagnostic performance (area under the receiver operating characteristic curve) for their convolutional long short-term memory model trained exclusively on VFs to assess glaucoma progression. This discrepancy was attributed to class imbalance in which achieving high accuracy is possible simply by performing well on stable cases. Although their model was limited to classifying the VF rather than predicting future VF defects, the same concept applies to MWen and MPark. We attempted to address this issue in our study by incorporating a no-change model in the evaluation phase. Likely because of the stability of most glaucoma patients, the no-change model performed well in comparison to our reimplemented models, if not the same or better. In fact, when the test set data for MPark was partitioned into the “worsening” category, the no-change model outperformed all MPark methods. This finding reveals how the predictive capabilities of a DL model may be severely limited in cases of the most clinical importance. Although patients with declining visual status would require more frequent monitoring and timely interventions, the DL algorithms failed to accurately foresee these patients’ VF deterioration.

Sorting the test data based on VF progression status confirmed that our data sets were highly imbalanced with the majority of samples classified as stable. However, attempting to balance the training data using oversampling and undersampling methods tended to result in significantly increased, not decreased, PMAEs. A possible reason for this result is that the test sets were highly imbalanced themselves; therefore, balancing the training sets inadvertently made them more dissimilar to the test sets that are used to determine the models’ accuracies. In this scenario, training on balanced data could produce worse prediction performance overall but better accuracy for progressing cases. Another potential explanation is that the minority data duplicated in the oversampling method were of low quality or unrepresentative of normal glaucoma progression. If so, the oversampling method would have multiplied any inherent errors or biases in the data, leading the algorithm further astray. Because of the increased variability of VFs in cases with more severe glaucomatous damage,²¹ it is possible that such variability introduced bias to the models and consequently resulted in lower performance. This finding highlights a notable difficulty with developing a practical DL model to aid clinicians in monitoring and treating glaucoma patients: having strong data sets that will enable an algorithm to perform well both on the majority of the clinical population that typically does not progress quickly and on the small but sizeable proportion of the population that does.¹⁹ Because DL models are able to learn only from the data they are provided, having large and robust data sets is vital to the algorithms’ performances.²² Developing such a data set to train and test future DL models will be imperative to achieving meaningful clinical translation of the algorithms.

In terms of forecasting worsening VFs, MWen achieved worse performance than MPark and was more similar to the no-change model (r = 0.94 vs. 0.73, respectively, Fig 7). Specifically, MWen’s achieved PMAEs increased with the difference in severity between the baseline and follow-up VFs: On average, there was a 0.93 dB increase in the error of the predicted VF with every 1 dB decrease in mean sensitivity between the supplied pair of VFs. That said, it is not possible to determine which DL approach is superior because the models used different subdata sets; the discrepancy between MWen’s and MPark’s accuracies for deteriorating VFs may be largely attributed to differences in input and output data. Because MPark required at least 6 consecutive VFs per patient, fewer patients could be used for this method: the MPark data set had approximately 4 times fewer patients than the MWen data set (1809 vs. 7472 patients). Furthermore, the MPark data set was deficient in stable cases unlike the MWen data set because most stable patients had only 2 or 3 total follow-up VFs. As a result, MPark was trained on a majority of worsening cases and could predict more accurate VFs for worsening glaucoma patients than MWen could. This finding again speaks to the importance of data set curation: If the data provided to a DL model are biased, the model’s results will ultimately reflect those biases.

Even the best-achieved PMAEs from our reimplementations are still inadequate for clinical practice, demonstrating that statistical significance does not necessarily translate into clinical significance. As aforementioned, MWen performed better than the no-change and ROP models at all 5 prediction time points on the overall test samples (P < 0.0001) and achieved its lowest PMAE of 2.05 dB (95% CI: 2.03 dB–2.07 dB) at year 1. However, even this lowest PMAE value is substantially greater than reported yearly rates of VF loss in glaucoma patients. Although figures vary widely among studies, median rates of VF loss in glaucoma patients treated in clinical practice have ranged anywhere from −0.05 dB/year to −0.62 dB/year,^19,23,24 and reports for mean rates of VF loss are more pessimistic. For instance, Heijl et al²⁵ analyzed the ROP of Early Manifest Glaucoma Trial patients randomized to the trial’s untreated control group and found an overall mean visual function loss of −1.08 dB/year. Although no consensus in definitions has been reached for levels of glaucoma progression, previous studies have defined very fast MD rates of progression in the range of −1.0 dB/year to −2 dB/year,^19,23,26,27 which is the same magnitude as the aforementioned lowest PMAE in our study. Therefore, even comparatively low PMAE values achieved by DL methods could result in large errors clinically.

Although these models used only VF data (as well as age in MWen) to generate their predictions, supplementing VF inputs with additional clinical data has previously been shown to improve machine learning models’ abilities to assess glaucoma progression.^20,28,29 Therefore, supplying information that is strongly associated with glaucoma onset and progression, such as intraocular pressure measurements, retinal nerve fiber layer thickness, cup-to-disc ratio, and family history, may better inform and improve future DL predictions. In addition, MWen may benefit from taking > 1 input VF into consideration like MPark does; because VF testing is notoriously unreliable because of its inherent variability and learning effect,^30,31 the model’s predictions could be led astray if the single baseline VF is not truly representative of the patient’s visual status. We attempted to mitigate this reliability issue in our study by excluding unreliable VFs from analysis, employing similar criteria (reliable VF tests defined as false-positive rate < 30%, false-negative rate < 30%, and fixation loss < 30%) to what Park et al⁹ used. However, false-positive rates exceeding 15% may significantly affect the reliability of VF measurements.³² Therefore, future VF prediction models may also benefit from utilizing stricter reliability criteria when curating data.

Our study had some limitations. For one, although we attempted to reimplement models described by Wen et al⁸ and Park et al⁹ as closely as possible, we did not have access to all their original codes. Therefore, we had to write our own code from scratch by following the papers’ methods sections. This resulted in similar but not identical algorithms, meaning that we were unable to truly externally validate the 2 models. In addition, our data sets were mainly composed of patients with less severe VFs. Although Wen et al⁸ reported an average baseline MD of −6.73 dB ± 6.23 dB and Park et al¹⁰ reported −7.02 dB ± 6.09 dB, our initial MD values were −2.74 dB ± 4.54 dB for MWen and −1.94 dB ± 3.49 dB for MPark. Because of these differences in data set composition, the original models may have been able to achieve better PMAEs on worsening cases than our reimplementations’ reported values. Finally, as aforementioned, our MPark data set contained significantly fewer patients and VF samples than our MWen data set. Although data augmentation can increase data set size and improve model performance,33, 34, 35 we did not employ such techniques in our study to remain consistent with the original methods. This is an important matter for future investigations on DL VF prediction models.

Our comprehensive assessment of 2 novel DL methods for VF progression from Wen et al⁸ and Park et al⁹ reveals that these models have statistical, but not necessarily clinical, significance. When analyzed based on VF progression status using an independent real-world data set, both models demonstrated poor predictive performance on worsening cases. As the accurate prognosis of glaucomatous progression and VF status is particularly important for patients experiencing severe VF decline, we recommend explicitly considering this aspect when developing and evaluating future DL models.