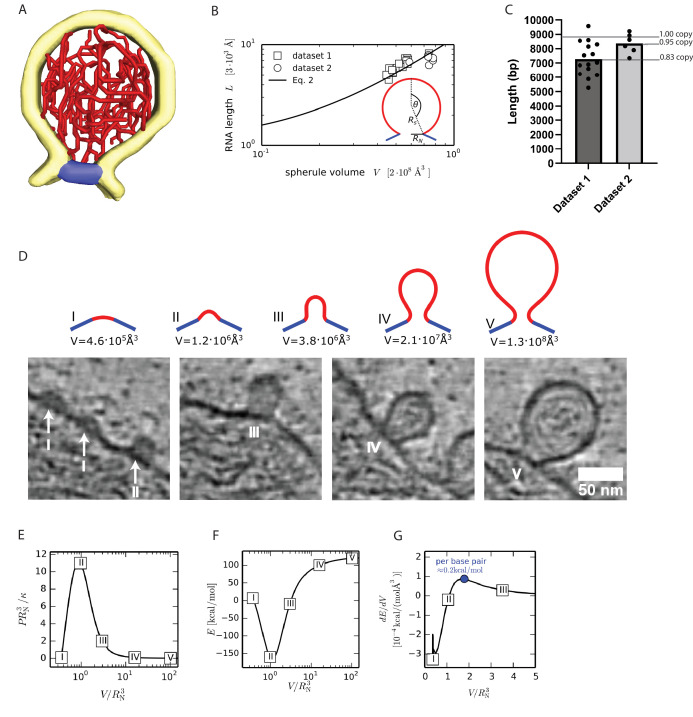
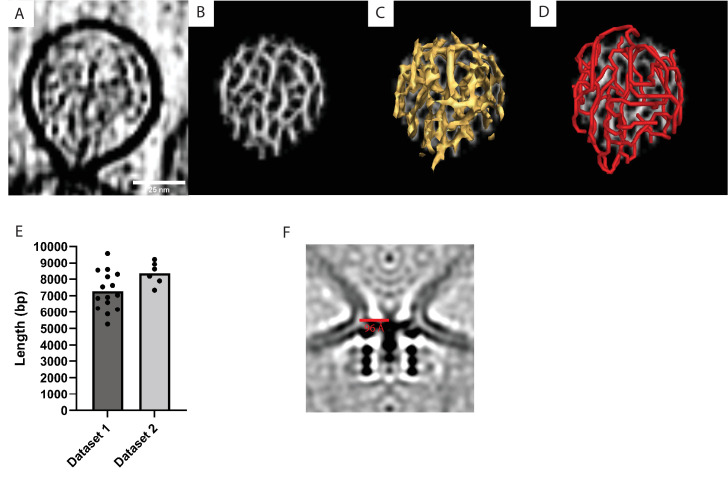
Figure 4. A single copy of the genomic RNA determines the shape of the spherule membrane.

(A) Segmentation of the dsRNA traced within a spherule. Yellow: membrane, red: RNA, and blue: neck complex base. (B) The RNA length L increases with spherule volume V. A common fit of both datasets with Equation 2 gives ${\displaystyle L_0=\left(3\pm 1\right)\cdot {10}^3\mathring{A}}$ and $\sigma R_N^2/\kappa =(4\pm 2)\cdot {10}^{-2}$, while ${\displaystyle R_N=96\mathring{A}}$ was determined experimentally. The inset shows the spherical cap model schematically. (C) Estimation of the dsRNA length (in base pairs) and the average copy number per spherule. One point represents a single spherule, and the datasets represents tomograms acquired on different cells. (D) The top row shows five shapes that minimize the energy (Equation 1) for a given spherule volume. Below, the predicted shapes are compared to different sizes of nascent and full-size spherules observed in cryo-electron tomograms of Semliki forest virus (SFV) viral replicon particle (VRP)-transduced cells. Scale bar, 50 nm. (E) Pressure-volume relation for a unitless membrane tension of a ${\sigma R}_N^2/\kappa$ = 10^–2. The corresponding membrane shapes are shown in subfigure D. (F) Energy (Equation 1) as a function of the spherule volume for ${\sigma R}_N^2/\kappa$ = 10^–2, κ=10 k_BT and ${\displaystyle R_N=96\mathring{A}}$. (G) The energy change per change in volume is shown, which leads to a maximal energy to be supplied per base pair of 0.2 kcal/mol, where we assumed the volume of a single base pair to be not larger than ${\displaystyle 2\cdot {10}^3{\mathring{A}}^3}$.

Figure 4—figure supplement 1. Tracing of RNA in the spherule lumen and membrane neck diameter.

(A) Slice through a tomogram highlighting the viral RNA in the spherule lumen. Scale bar, 25 nm. (B) The output of the cylinder correlation operation on the volume shown in (A), as performed in Amira’s filament tracing module (Rigort et al., 2012). (C) Isosurface view of (B). (D) Filament model generated by correlation line tracing of the volume shown in (B). (E) Length of the traced RNA in Ångström. One dot corresponds to an individual spherule, and the bars represent the average value in each dataset (being tomograms acquired on different cells). (F) The radius of the neck of a spherule is 96 Å.

Figure 4—figure supplement 2. Dependence of the total filament length on filament tracing parameters.

(A) Length of the cylinder templates used for cross-correlation calculation. A value of 6 nm was used in this study. (B) Radius of the outer cylinder mask. A value of 3.5 nm was used. (C) Maximum allowed angle between adjacent cylinder fragments during the tracing. A value of 5° was used. (D) Cutoff value for the seed correlation between points following the RNA in cryo-tomograms. A value of 65 was used.

Figure 4—figure supplement 3. Spherule shape parameterization.

(A) The spherule shape is parameterized by the arc length and the azimuthal angle $\psi$, where we consider a cylindrically symmetric shape. (B and C) Values for $h_0$ and $s_{end}$ that solve the shape equations, Equation (T17) with the boundary conditions, Equation (T19) for $\tilde{\sigma }=0.01$.