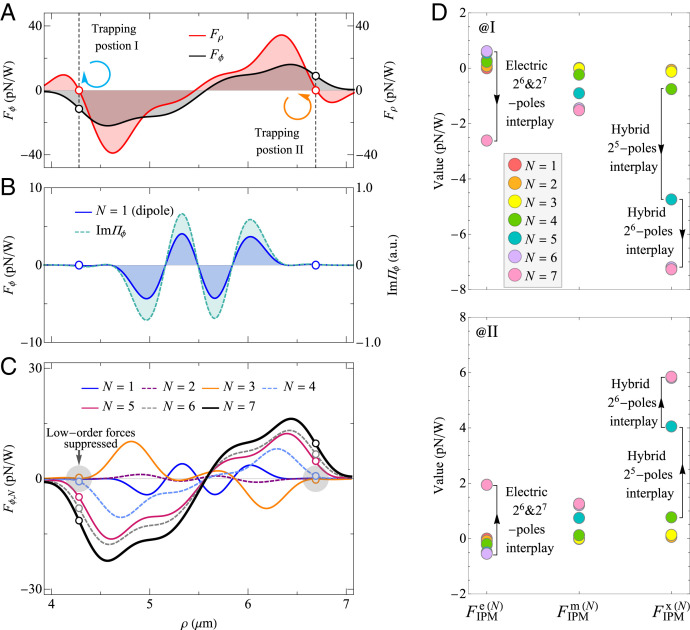
Fig. 2.

Theoretical results of optical forces for α = −45° (the IPM vortex condition). (A) Radial and azimuthal forces, F_ρ and F_ϕ, versus the radial displacement of the gold sphere. The truncation index in these calculations is N = 7, which is large enough to ensure the convergence of the Mie series. Hollow dots mark the values at radial equilibrium positions I and II, where the radial force vanishes with a negative derivative. (B) Comparison of the dipolar component of F_ϕ with incident IPM. (C) Azimuthal force for different N showing that low-order contributions are small at the equilibrium positions. (D) Calculated electric $F_{\mathrm{IPM}}^{\mathrm{e}\left(N\right)}$, magnetic $F_{\mathrm{IPM}}^{\mathrm{m}\left(N\right)}$, and hybrid $F_{\mathrm{IPM}}^{\mathrm{x}\left(N\right)}$ components of the IPM force at the trapping positions I and II, for different N. All components are in the azimuthal direction. In each channel, the difference between the components with adjacent N indicates the contribution from specific multipolar interaction: $F_{\mathrm{IPM}}^{\mathrm{e}\left(N\right)}-F_{\mathrm{IPM}}^{\mathrm{e}(N-1)}$ (or $F_{\mathrm{IPM}}^{\mathrm{m}\left(N\right)}-F_{\mathrm{IPM}}^{\mathrm{m}(N-1)}$) represents the electric (or magnetic) IPM force, due to the interplay of the electric (or magnetic) 2^N-pole with 2^N−1-pole; $F_{\mathrm{IPM}}^{\mathrm{x}\left(N\right)}-F_{\mathrm{IPM}}^{\mathrm{x}(N-1)}$ gives the hybrid IPM force caused by the interference between electric and magnetic 2^N-poles.