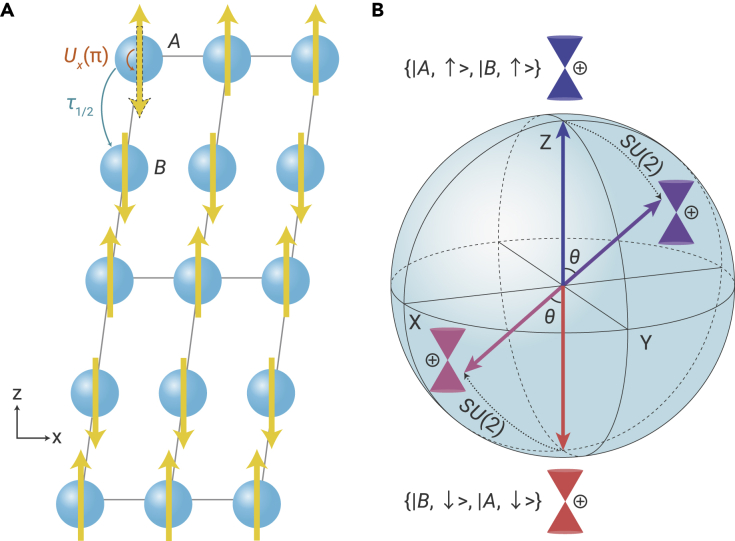
Figure 2.

Hidden $\mathit{SU}\left(2\right)$ symmetry in antiferromagnetic materials

(A) The magnetic lattice with collinear antiferromagnetic order allows spin-group symmetry operations, $\left\{U_x\left(\pi \right)|\left|E\right|{\mathit{\tau }}_{1/2}\right\}\text{ and }\left\{U_z\left(\theta \right)|\left|E\right|0\right\}$ without spin-orbit coupling, leading to two degenerate Weyl cones with the basis $\left\{|A,\uparrow ⟩,|B,\uparrow ⟩\right\}$ and $\left\{|B,\downarrow ⟩,|A,\downarrow ⟩\right\}$ and an $SU\left(2\right)$ symmetry group $exp\left(-i\theta \mathit{n}\cdot \mathit{\rho }\right)$ (see the main text).

(B) Bloch sphere of the $SU\left(2\right)$ symmetry group, transforming the basis of a Weyl cone $\left\{|A,\uparrow ⟩,|B,\uparrow ⟩\right\}$ (blue arrow) to any linear combinations (up to a phase factor) $\left\{\alpha \left|A,\uparrow ⟩+\beta \right|B,\downarrow ⟩,\alpha |B,\uparrow ⟩+\beta |A,\downarrow ⟩\right\}$, and transforming $\left\{|B,\downarrow ⟩,|A,\downarrow ⟩\right\}$ (red arrow) to an orthogonal one $\left\{-{\beta }^{\ast }\left|A,\uparrow ⟩+{\alpha }^{\ast }\right|B,\downarrow ⟩,-{\beta }^{\ast }|B,\uparrow ⟩+{\alpha }^{\ast }|A,\downarrow ⟩\right\}$. The basis transformation under the rotation axis (gray line) $\mathit{n}=(cos\left(\omega \right),sin\left(\omega \right),0)$ and rotation angle $\theta$ are also shown. The mixing coefficients are $\alpha =cos\left[\theta /2\right]$ and $\beta =-isin\left[\theta /2\right]e^{-i\omega }$.