Comparison of the United- and All-Atom Representations of (Halo)alkanes Based on Two Condensed-Phase Force Fields Optimized against the Same Experimental Data Set

Abstract

The level of accuracy that can be achieved by a force field is influenced by choices made in the interaction-function representation and in the relevant simulation parameters. These choices, referred to here as functional-form variants (FFVs), include for example the model resolution, the charge-derivation procedure, the van der Waals combination rules, the cutoff distance, and the treatment of the long-range interactions. Ideally, assessing the effect of a given FFV on the intrinsic accuracy of the force-field representation requires that only the specific FFV is changed and that this change is performed at an optimal level of parametrization, a requirement that may prove extremely challenging to achieve in practice. Here, we present a first attempt at such a comparison for one specific FFV, namely the choice of a united-atom (UA) versus an all-atom (AA) resolution in a force field for saturated acyclic (halo)alkanes. Two force-field versions (UA vs AA) are optimized in an automated way using the CombiFF approach against 961 experimental values for the pure-liquid densities ρ_liq and vaporization enthalpies ΔH_vap of 591 compounds. For the AA force field, the torsional and third-neighbor Lennard–Jones parameters are also refined based on quantum-mechanical rotational-energy profiles. The comparison between the UA and AA resolutions is also extended to properties that have not been included as parameterization targets, namely the surface-tension coefficient γ, the isothermal compressibility κ_T, the isobaric thermal-expansion coefficient α_P, the isobaric heat capacity c_P, the static relative dielectric permittivity ϵ, the self-diffusion coefficient D, the shear viscosity η, the hydration free energy ΔG_wat, and the free energy of solvation ΔG_che in cyclohexane. For the target properties ρ_liq and ΔH_vap, the UA and AA resolutions reach very similar levels of accuracy after optimization. For the nine other properties, the AA representation leads to more accurate results in terms of η; comparably accurate results in terms of γ, κ_T, α_P, ϵ, D, and ΔG_che; and less accurate results in terms of c_P and ΔG_wat. This work also represents a first step toward the calibration of a GROMOS-compatible force field at the AA resolution.

1. Introduction

Classical atomistic simulations¹⁻³ and, in particular, molecular dynamics⁴⁻⁸ (MD) have become an established tool complementary to experiment for the investigation of condensed-phase systems. The accuracy of such simulations depends crucially on the quality of the underlying potential-energy function or force field.⁹⁻¹⁶ A force field is characterized by two main design components: the choice of a functional form for the potential energy and the value of the associated parameters.

In terms of functional form, the “basic” versions of the most popular condensed-phase force fields such as GROMOS,¹⁷⁻²² OPLS,²³⁻²⁶ CHARMM,²⁷⁻³² AMBER,³³⁻³⁷ OpenFF,³⁸⁻⁴⁰ or TraPPE⁴¹⁻⁴³ have many features in common. However, numerous variants of these (and other) force fields have also been developed, differing by specific elements of the interaction-function design, and referred to here as functional-form variants (FFVs). Common FFVs are related in particular to the following aspects: aliphatic groups⁴⁴⁻⁵⁵ [united-atom (UA) or all-atom (AA) resolution], covalent anharmonicities and cross-terms,⁵⁶⁻⁶⁰ coupled torsional terms,^50,61−66 rules for close covalent neighbors⁶⁷⁻⁷⁰ (exclusions, scalings, and exceptions), van der Waals functions⁷¹⁻⁸² (and possible anisotropy^55,83−87), combination rules^{74,75,80,88−97} (or their partial by-passing), electrostatic multipole orders,^85,98−104 short-range charge penetration effects,^{74,79,105−111} off-atom electrostatic sites,^104,112,113 conformation-dependent charge fluxes,^{60,67,114,115} many-body interactions,⁸¹ and electronic polarization.^116−118

A number of choices commonly considered to be part of the simulation protocol^119,120 actually also represent FFVs as they actually enter into the specification of the potential-energy function. These include in particular the possible use of covalent-coordinate constraints^121−128 (rigid or flexible bonds and/or bond angles), the cutoff distances applied to define the short-range van der Waals and electrostatic interactions, the cutoff truncation mode (atom- or group-based^120,129,130), the possible cutoff modifications (switching^27,131−134 or shifting^{27,132,134−139}), and the treatment of the long-range van der Waals^96,140−144 and electrostatic^145−147 interactions (neglect, mean-field, or lattice-sum). Considering the critical importance of aqueous solutions, one might even view the water model compatible with a force field as belonging to the FFVs.¹⁴⁸

In turn, the selection of appropriate values for the parameters of the potential-energy function is affected by three main design features of the force field: (i) the choices made for all the FFVs (see above), (ii) the procedure used to calibrate the parameters (e.g., derivation recipes for charges^149−154 and/or van der Waals parameters,^113,155,156 choice of target observables^22,157,158), and (iii) the target data used in the calibration (experimental and/or quantum-mechanical data, molecules in the training set). Ideally, the force-field parameters should be fully optimized for best possible agreement between simulation results and target data given the three above choices. However, this optimality is not guaranteed when heuristic procedures are employed to refine the parameters. As an illustrative example, the inability of the GROMOS 53A5 and 53A6 parameter sets to reproduce both the pure-liquid and hydration properties of small organic molecules¹⁹ could be relieved in the GROMOS-compatible 2016H66 parameter set²² by performing the optimization of the van der Waals parameters and charges simultaneously.¹⁵⁹ Even when automated calibration procedures are employed,^{157,158,160−170} optimality remains challenging to guarantee due to the likely presence of multiple local optima in parameter space. This issue can be addressed to some extent by undertaking independent calibration runs starting from different initial parameters.^157,164

Owing to the intricate correlation between FFVs, calibration procedure, target data, and (near-)optimal force-field parameters, assessing the impact of one specific FFV on the accuracy of the force-field representation is a difficult task. Many studies in the literature report comparison benchmarks (i.e., considering a given set of systems and properties) involving different condensed-phase force fields.^{51,144,171−186} However, even assuming that two force fields have (near-)optimal parameters within their specific FFVs, an assumption that is in itself highly questionable, a change of force field generally involves changing many FFVs simultaneously. For example, when comparing a polarizable force field A and a pairwise-additive force field B, the observation that A is more accurate than B (or the opposite) in some benchmark comparison does not represent a proof for the importance (or irrelevance) of an explicit polarization treatment on the accuracy of the force-field representation in general.

Equally problematic is the alternative comparison involving the change of one specific FFV within a given force field without adjusting its parameters. Here, even FFV changes expected to enhance the accuracy of the interaction function may actually turn out to be detrimental when the force-field parameters are not reoptimized accordingly. Illustrative examples of this kind include the change from united- to all-atom resolution,¹⁸² the use of a longer cutoff for the non-bonded interactions,^119,187 the introduction of long-range non-bonded corrections,^{119,144,187,188} the application of a self-polarization correction,¹⁸⁹ or the explicit representation of electronic polarization.¹⁹⁰

Because it is so difficult to disentangle the effect of one specific FFV on the accuracy of the force-field representation in general, different research groups place a particular emphasis on correcting for one or the other shortcoming of the “basic” functional form, that is, the one they assume to be the most critical. However, providing unambiguous support for such an assumption would require comparing two force fields differing exclusively in terms of the specific FFV and both relying on an optimal parameterization against the same target data. Clearly, the latter requirement may prove extremely challenging to achieve in practice, considering the high complexity of the force-field calibration task (implicit design choices, optimality difficult to guarantee). In two recent articles,^157,158 we have introduced an approach called CombiFF, which could serve precisely this purpose.

The CombiFF scheme¹⁵⁷ is designed for the automated refinement of force-field parameters against experimental condensed-phase data considering entire classes of organic molecules. The main steps of the scheme are (i) definition of a molecule family, (ii) enumeration of all isomers, (iii) query for experimental data, (iv) construction of the molecular topologies by fragment assembly, and (v) iterative refinement of the force-field parameters considering the entire family. As an initial application, CombiFF was used to calibrate GROMOS-compatible UA force fields for saturated acyclic compounds with halogen substitutions,¹⁵⁷ as well as for oxygen and nitrogen functional groups,¹⁵⁸ by calibrating against a large set of experimental pure-liquid densities ρ_liq and vaporization enthalpies ΔH_vap. Given the favorable observable-to-parameter ratio, the non-bonded parameters are optimized exclusively based on these values, without relying on any quantum–mechanical (QM) calculations. The required number of iterations remains limited (on the order of 10) and the optimization can be parallelized, so that the complete refinement of a parameter set only takes a few days of wallclock computational time.

A key feature of CombiFF in the present context is that once the time-consuming task of target-data selection/curation has been performed, the parameter calibration can easily be repeated for any choice in the FFVs. Thus, the intrinsic effect of an FFV on the accuracy of the force-field representation can be assessed at optimal parameterization against the same target data. Here, this possibility is exploited in the context of the saturated acyclic (halo)alkanes and considering the choice of a UA or an AA force-field resolution as the FFV of interest.

The UA representation is a form of coarse graining where (a subset of) the hydrogen atoms in a molecule are represented implicitly by adjusting of the interaction terms involving the heavy atoms carrying them. This representation was introduced early in the area of molecular simulation,⁴⁴ mainly because it was compatible with the absence of hydrogen coordinates in (bio-)molecular structures from X-ray crystallography. The early versions of the main condensed-phase force fields relied on the UA representation, albeit restricted to the aliphatic (sometimes also the aromatic) hydrogen atoms, so as to preserve an accurate description of hydrogen-bonding properties.

The two main advantages of the UA representation for aliphatic groups are (i) a reduction in the number of explicitly represented atoms and (ii) the removal of the high-frequency bond/angle vibrations involving these hydrogen atoms. This permits to reduce the computational cost both directly (fewer atoms) and indirectly (longer timestep). The three assumptions underlying the UA representation are that (i) the vibrations involving the hydrogen atoms are not excited (QM ground state), (ii) the contribution of these atoms to the multipole moments and hydrogen-bond donor capacity of the aliphatic group is negligible, and (iii) these atoms do not induce a significant anisotropy in the van der Waals envelope of the aliphatic group. The first assumption is typically fulfilled at room temperature, but the latter two are approximate in nature. Taking the extreme example of polar hydrogen atoms, neglecting the dipolar component would disregard the possibility of hydrogen bonding. To a lesser extent, the same applies to aromatic hydrogen atoms in the context of electrophile−π interactions.

Popular condensed-phase force fields nowadays typically provide an AA alternative to the initial UA version (see, for example, TraPPE-UA⁴¹ vs TraPPE-AA¹⁹¹), with GROMOS being an exception. The most recent generalized force fields (i.e., involving automated topology-building schemes and a large chemical-space coverage) all rely on an AA description, for example OPLS-AA²⁴ (via TPPMKTOP¹⁹²), CHARMM-CgenFF^193,194 (via CHARMM-GUI^29,195−197), AMBER-GAFF³⁶ (via Antechamber¹⁹⁸), and OpenFF^38−40,199 (see ref (200)).

The arguments commonly invoked in favor of the AA resolution are (i) a better representation of the thermodynamic properties, (ii) a better representation of the transport properties (UA models tend to be too diffusive^22,182), (iii) a better representation of directional interactions²⁴ (aliphatic hydrogen atom as a weak hydrogen-bond donor), (iv) a simpler description of the covalent (torsional dihedrals easier to define, improper dihedrals not needed) and of the non-bonded (single C and H atom types rather than multiple CH_n UA types) interactions,²⁴ and (v) a limited computational overhead relative to UA for aqueous systems (cost dominated by water–water interactions).

Although generally correct, these arguments are still matters of discussion. First, the relative adequacies of the UA and AA resolutions are still debated (see further below). Second, the diffusivity enhancement (a common consequence of coarse graining^201−203) may actually represent a sampling advantage when only thermodynamic properties are of interest. Third, the computational overhead of the AA representation may remain very significant for aliphatic-rich systems such as organic liquids or lipid membranes. Finally, AA models are typically affected by overestimated heat capacities^22,174 due to the representation of the vibrations involving hydrogen atoms by classical harmonic oscillators²² (with an equipartition contribution k_B to the heat capacity vs zero for a QM oscillator in the ground state). These discrepancies can be alleviated by adding a quantum correction to the AA results.^{174,204−206} However, since the heat capacity determines the temperature derivatives of the thermodynamic properties, a discrepancy in the uncorrected results may still impair the transferability of the force field in temperature. This issue can be alleviated at the AA level by enforcing entirely rigid geometries for the aliphatic groups. In this case, it may be computationally advantageous to represent the corresponding hydrogen atoms as virtual sites.^50,53,54

The question whether the AA representation is really superior to the UA representation in terms of reproducing thermodynamic (e.g., pure-liquid, solvation) properties has been debated. It represents a prototypical situation where the assessment of an FFV at a suboptimal level of parameterization can be misleading. For example, in ref (45), it is argued that the AA representation is essential for reproducing the hydration properties of small amines. However, in ref (207), it is shown that a UA model can lead to equally accurate results provided that it is appropriately parameterized. Numerous other studies have compared the relative merits of the UA and AA representations.^{47−55,174,181−183,208−210} Besides the differences related to the diffusivity and the heat capacity (see above), most of these studies suggest that the bulk thermodynamic properties can be reproduced similarly well at the two levels of resolution.

In the present study, we compare the accuracies of two force-field variants for saturated acyclic (halo)alkanes, calibrated and validated using the CombiFF approach against experimental data for ρ_liq and ΔH_vap, namely 347 data points concerning 196 compounds for calibration and 614 data points concerning 395 additional compounds for validation. One variant relies on the UA resolution and is the one previously described in ref (157). The other variant is refined here and corresponds to the AA resolution, also including a readjustment of the torsional parameters against QM rotational profiles. In practice, the comparison of the AA and UA models still remains somewhat imperfect due to a possible residual suboptimality of the parameters and to specific implicit design choices (e.g., atom-type sets in the two models, restriction of the optimization to a subset of parameters). Nevertheless, compared to a heuristic calibration approach, the use of CombiFF takes us much closer to performing a comparison at the optimal parameterization level.

The optimized force fields are compared not only in terms of the calibration properties ρ_liq and ΔH_vap but also in terms of other thermodynamic and transport properties, namely the surface-tension coefficient γ, the isothermal compressibility κ_T, the isobaric thermal-expansion coefficient α_P, the isobaric heat capacity c_P, the static relative dielectric permittivity ϵ, the self-diffusion coefficient D, the shear viscosity η, the hydration free energy ΔG_wat, and the free energy of solvation ΔG_che in cyclohexane. Besides the UA versus AA comparison, this work also represents a first step toward the calibration of a GROMOS-compatible force field at the AA resolution.

2. Computational Details

2.1. Molecule Selection and Experimental Data

Two families of compounds are considered here, with molecules including up to 10 carbon atoms, namely saturated acyclic alkanes (ALK) and haloalkanes (HAL). Both families are divided into a calibration set (CAL) and a validation set (VAL). In total, 591 molecules are included. The distribution of these compounds into the four sets is summarized in Table 1, and the corresponding structures are displayed in Supporting Information Section S.1 (Figures S.1–S.4). The relevant experimental values are provided in Supporting Information Section S.2 (Tables S.1 and S.2). These values (along with the GROMOS-compatible coordinate and topology files) can also be downloaded from the Internet under ref (211). Note that only constitutional isomers are distinguished here, not stereoisomers. This does not represent a serious issue as the vast majority of the molecules considered have at most one stereogenic center (see Supporting Information Section S.2 of ref (157)).

Table 1. Four Sets of (Halo)alkanes Considered in the Present Work^a.

fam.	n	m	k	Niso	Nsim	Nexp	description
ALK-CAL	1–6	0	0	13	11	25	C1–C6 alkanes
ALK-VAL	7–10	0	0	137	137	274	C7–C10 alkanes
HAL-CAL	2–4	1–3	1	172	114	217	C2–C4 mono- or homo-di,tri-halogenated
HAL-CAL	2–4	2–4	2	1764	41	60	C2–C4 hetero-di,tri,tetra-halogenated with exactly two halogen types
HAL-CAL	5	1	1	12	9	12	C5 mono-halogenated with X on secondary C (R2−CHX with R ≠ H)
HAL-CAL	5–6	1	1	16	13	22	C5–C6 mono-halogenated with X on tertiary C (R3−CX with R ≠ H)
HAL-CAL	5	1–3	1	12	6	8	C5 mono- or homo-di,tri-halogenated of the form tBu–CHiX3–i
HAL-CAL	6	1	1	4	2	3	C6 mono-halogenated of the form tBu–CHX–CH3
HAL-VAL	5–10	1–3	1	62,964	251	333	C5–C10 mono- or homo-di,tri-halogenated (except those already included)
HAL-VAL	5–9	2–4	2	666,534	6	6	C5–C9 hetero-di,tri,tetra-halogenated with exactly two halogen types
HAL-VAL	10	2	2	23,754	1	1	C10 hetero-di-halogenated with exactly two halogen types

^aThese correspond to the calibration set (CAL) and the validation set (VAL) for saturated acyclic alkanes (ALK) and haloalkanes (HAL). The sets are defined in terms of 11 non-overlapping groups. All compounds have the chemical formula 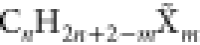with 1 ≤ n ≤ 10 and 0 ≤ m ≤ 4, where stands for an arbitrary combination of m halogen atoms X ∈ {F,Cl,Br,I}. The value of k restricts the number of halogen types allowed in this combination (e.g., m = 3 and k = 2 indicates that the compound includes three halogen atoms which are of two different types). The total number N_iso of constitutional isomers, the number N_sim of isomers actually considered in the simulations, and the number N_exp of experimental values available for either ρ_liq or ΔH_vap are also indicated for each group. For the alkanes, only methane and ethane are excluded from the set of isomers. For the haloalkanes, N_sim is limited by the availability of experimental data for ρ_liq and/or ΔH_vap. The structures of the 591 compounds are displayed in Supporting Information Section S.1 (Figures S.1–S.4). The reference experimental values retained for ρ_liq and/or ΔH_vap (also including methane and ethane), along with the associated P,T-points, are reported in Supporting Information Section S.5 (Tables S.5 and S.6).

The ALK-CAL set consists of 11 molecules, namely all the alkane isomers with up to 6 carbon atoms excluding methane and ethane, and the ALK-VAL set consists of 137 molecules, with all the isomers involving 7–10 carbon atoms. The HAL family is the same as the one considered in our previous article¹⁵⁷ but excludes the molecule B4312 (due to issues with the reference data) as well as the 42 halomethane molecules.

The HAL-CAL set consists of 185 molecules with up to 6 carbon atoms, and the HAL-VAL set consists of 258 molecules with 5–10 carbon atoms. The two latter sets only cover a tiny fraction of the possible constitutional isomers, namely about 2.8 × 10¹³ saturated haloalkanes with up to 10 carbon atoms (see Supporting Information Section S.2 of ref (157)). The smallest molecules (methane, ethane, halomethanes) were excluded after initial parameterization attempts, which revealed the need for AA parameters distinct from those employed in the larger molecules, in line with observations made in previous studies.^157,212,213

The reference experimental ρ_liq and ΔH_vap values for the saturated haloalkanes were collected from refs (214–218) and selected/curated as described in Appendix A of ref (157). The corresponding data for the alkanes were collected from refs (214–216, 218, and 219), and processed analogously. In total, the number of experimental values collected for either ρ_liq or ΔH_vap is 25 (CAL) and 274 (VAL) for the ALK set, and 322 (CAL) and 340 (VAL) for the HAL set. The reference experimental values retained for ρ_liq and/or ΔH_vap, along with the associated P,T-points, are reported in Supporting Information Section S.5 (Tables S.5 and S.6).

2.2. Force-Field Representation and Parameterization

Both the UA and AA force-field variants rely on the standard functional form and simulation parameters of the GROMOS force field.^{18−22,119,157,220−223} This includes in particular GROMOS-compatible choices made for the bond description (constraints^121,122,224), bond-angle bending potential (cosine-harmonic¹⁸), van der Waals potential [Lennard-Jones (LJ)],²²⁵ combination rule (geometric mean^226,227), non-bonded exclusions (first and second covalent neighbors), third-neighbor interactions (full electrostatics, reduced LJ), long-range non-bonded interactions (reaction-field electrostatics,^228,229 no long-range LJ correction¹¹⁹), cutoff truncation (twin-range,²³⁰ 0.8/1.4 nm cutoff,¹⁸ charge-group-based^120,129), and water model (simple point charge SPC model²³¹).

The only significant change relative to standard GROMOS is that the atomic partial charges are specified indirectly¹⁵⁷ via the parameters of an electronegativity equalization (EE) scheme.²³² To permit the definition of neutral charge groups, the EE charge transfers are kept local.¹⁵⁷ In the UA variant, they are only performed across C–X bonds, resulting in neutral charge groups of at most four atoms (when omitting the halomethanes). The non-halogenated aliphatic (united-)atoms are defined as separate charge groups with zero charge. In the AA variant, charge transfers are only performed across C–X and C–H bonds, also resulting in neutral charge groups of at most four atoms (when omitting methane and the halomethanes).

Given the choice of an EE scheme for generating the atomic partial charges and the application of a geometric-mean combination rule^226,227 for the LJ interactions,²²⁵ each atom type in the force field is associated with four non-bonded interaction parameters, namely the LJ collision diameter σ, the LJ well depth ϵ, the EE hardness η, and the EE electronegativity χ.

The UA force-field variant and its calibration procedure have already been described in our previous article.¹⁵⁷ This variant involves 19 covalent interaction parameters (including those of a common torsional-dihedral type applied to all C–C bonds) and 56 non-bonded interaction parameters (4 × 13 parameters characterizing 13 atom types, plus four alternative σ parameters for third-neighbor interactions involving the aliphatic types CH0–CH3). Only the non-bonded interaction parameters of the non-aliphatic types, that is, those for the halogen atoms and the halogenated carbon (united-)atoms, were subject to optimization (32 parameters). Their calibration was performed automatically using the CombiFF scheme¹⁵⁷ based on 484 experimental values for ρ_liq and 265 experimental values for ΔH_vap, pertaining to 228 (calibration) and 258 (validation) molecules. The aliphatic types were not reoptimized relative to the current GROMOS parameters (identical in the 54A7 set²⁰ and the 2016H66 set²²) as these parameters have been previously optimized^233,234 against experimental data for ρ_liq and ΔH_vap, as well as solvation free energies in water and cyclohexane. In addition, these united-atoms are kept neutral so that no η and χ values are required.

The AA force-field variant and its calibration are the focus of the present article. This variant involves 58 covalent interaction parameters (including those for 12 torsional-dihedral types) and 33 non-bonded interaction parameters (4 × 8 parameters characterizing 8 atom types, plus 1 alternative σ parameter for third-neighbor interactions involving carbon atoms).

As was the case for the UA force field,¹⁵⁷ the covalent parameters for bond stretching and bond-angle bending were not subject to optimization. They were either imported from the OPLS-AA force field²⁴ for terms involving exclusively carbon and hydrogen atoms (10 parameters) or taken from the UA variant¹⁵⁷ for terms involving halogen atoms (12 parameters). The values of these parameters are reported in Table 2. Note that the bond-stretching force constants are irrelevant in the present work since all bonds are constrained. The parameters of 12 torsional-dihedral potentials pertaining to 10 different C–C bond substitutions (Figure 1) were optimized along with the aliphatic-carbon third-neighbor LJ parameters against QM rotational profiles, as described later in Section 2.3. The final (optimized) values of the corresponding parameters are also reported in Table 2.

Table 2. Covalent Types of the Saturated (Halo)alkane Force Field in Its AA Variant and Final (Optimized) Values of the Associated Parameters^a.

bond
quartic force constant [106 kJ·mol–1·nm–4]	reference bond length [nm]	usage
1.197	0.109	C–H
4.796	0.153	C–C
15.089	0.133	C–F
8.120	0.176	C–Cl
6.950	0.192	C–Br
5.669	0.216	C–I

angle
cosine-harmonic force constant [kJ·mol–1]	reference bond angle [deg]	usage
305.0	107.8	H–C–H
359.0	110.7	H–C–C
575.0	112.7	C–C–C
359.0	109.0	H–C–X
618.0	109.5	X–C–C, X–C–X

torsional dihedral
force constant [kJ·mol–1]		phase shift [deg]	multiplicity	usage
(a)	5.316	0	3
(b)	4.708	0	3
(c)	3.900	0	3
(d)	3.245	0	3
(e)	3.612	0	3
(e)	1.865	0	1
(f)	1.820	0	3
(g)	1.524	0	3
(h)	2.387	180	1
(h)	1.194	0	2
(i)	0.218	0	3
(j)	2.030	0	3

third-neighbor LJ interaction
σ [nm]	ϵ [kJ·mol–1]	usage
0.253	0.224	C–(C)–(C)–H,C,X (third neighbors)

^aThe covalent types are listed along with their usage and the values of the interaction parameters. These are force constants, along with reference bond lengths or angles, multiplicities, and phase-shift angles for the torsions. The symbol X stands for any halogen atom (F, Cl, Br, I). The parameters of the 12 torsional-dihedral potentials correspond to the 10 different C–C bond substitutions shown in Figure 1. The notations 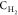, , 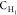and 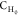refer to carbon atoms bearing 2, 1, and 0 hydrogen atoms, respectively, along with 1, 2, and 3 atoms of the types shown before or after the dash (e.g., the type 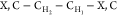applies to a fragment R′,R–CH₂–CH–R,R′, where R and R′ are of atom type C or X). The one (or two) terms of the potential is applied only once around a given C–C bond. This single dihedral is selected based on the two groups substituting the C–C bond according to the decreasing priority: isopropyl, ethyl, methyl, tert-butyl, F, Cl, Br, I, and H. The LJ collision diameter σ and well depth ϵ to be used in the combination rule for an aliphatic (non-halogenated) carbon atom interacting with any of its third neighbors (irrespective of whether it is hydrogen, carbon, or halogen) are also reported. Note that this entry is repeated in Table 3. Solely, the torsional and third-neighbor aliphatic carbon parameters were subject to optimization. The initial values of the torsional parameters (at the start of the calibration) can be found in Supporting Information Section S.3 (Table S.3).

Figure 1.

Different C–C bond substitutions relevant for the assignment of the torsional-dihedral potentials of the saturated (halo)alkane force field in its AA variant. The drawings (a–j) illustrate the 10 different substitutions corresponding to the 12 torsional-dihedral potentials of Table 2. Except for drawings (a–d), only non-hydrogen atoms (carbon or halogen) are shown in the C–C substitutions. The potential is applied only once around a given C–C bond and involves only one term, except for (e,h), which involve two terms. This single dihedral is selected based on the two groups substituting the C–C bond according to the decreasing priority: isopropyl, ethyl, methyl, tert-butyl, F, Cl, Br, I, and H. Special values of the LJ collision diameter σ and well depth ϵ (also reported in Table 2) are to be used in the combination rule for an aliphatic (non-halogenated) carbon atom interacting with any of its third neighbors (irrespective of whether it is hydrogen, carbon, or halogen).

The 32 non-bonded interaction parameters associated with the 8 atom types of the force field were fully optimized, as described later in Section 2.4. The final (optimized) values of these parameters are reported in Table 3. The ALK family relies on two atom types, one for the carbon atom and one for the hydrogen atom. The HAL family requires six additional types, one for each type of halogen atom (F, Cl, Br, I), one for the halogenated carbon atom, and one for the hydrogen atom when connected to a halogenated carbon atom. Special third-neighbor LJ parameters were only introduced and optimized for the aliphatic (non-halogenated) carbon atom.

Table 3. Atom Types of the Saturated (Halo)alkane Force Field in Its AA Variant and Final (Optimized) Values of the Associated Parameters^a.

atom type	σ [nm]	ϵ [kJ·mol–1]	η [e–1 V]	χ [V]	usage
C	0.332	0.318	15.938	21.694	aliphatic (non-halogenated) carbon
	0.253	0.224			idem, third-neighbor
H	0.255	0.126	18.475	13.542	hydrogen on aliphatic (non-halogenated) carbon
CX	0.309	0.359	31.375	13.754	halogenated carbon
HX	0.235	0.179	48.519	10.107	hydrogen on halogenated carbon
F	0.299	0.374	44.440	25.617	fluorine
Cl	0.347	1.264	39.032	21.173	chlorine
Br	0.367	1.817	35.628	18.468	bromine
I	0.396	2.360	39.078	17.358	iodine

^aThe eight atom types are listed along with their usage and the values of the non-bonded interaction parameters. These are the Lennard-Jones (LJ) collision diameter σ and well depth ϵ, along with the electronegativity-equalization (EE) hardness η and electronegativity χ. The LJ collision diameter σ and well depth ϵ to be used in the combination rule for an aliphatic (non-halogenated) carbon atom interacting with any of its third neighbors (irrespective of whether it is hydrogen, carbon, or halogen) are also reported. Note that this entry is repeated in Table 2. The initial values of the non-bonded interaction parameters (at the start of the calibration) can be found in Supporting Information Section S.3 (Table S.4).

2.3. Calibration of the Torsional Parameters

For the AA variant, the parameterization of the torsional potentials was performed against QM rotational-energy profiles calculated for alkane molecules of 2 to 8 carbon atoms, representative of the 10 relevant C–C bond substitutions of Figure 1.

The reference QM profiles correspond to energies calculated in vacuum (no continuum solvent) at the MP2 level of theory²³⁵ using a 6-311G(dp) basis set²³⁶ for the structure optimization and an aug-cc-pVTZ basis set^237,238 for the energy calculation. This represents an affordable alternative to performing the full calculation with an aug-cc-pVTZ basis set and leads to comparable energies (as was tested in a few cases; data not shown). A single molecule was used to calibrate each dihedral type. These molecules are ethane (A2001), propane (A3001), 2-methylpropane (A4001), 2,2-dimethylpropane (A5001), butane (A4002), 2-methylbutane (A5002), 2,2-dimethylbutane (A6001), 2,3-dimethylbutane (A6002), 2,2,3-trimethylbutane (A7001), and 2,2,3,3-tetramethylbutane (A8001), respectively, for the types (a–j) of Figure 1. The sampling was performed using 36 equidistant points over the period 0–360°.

The fitting of the torsional-energy parameters was performed simultaneously with that of the aliphatic-carbon third-neighbor LJ parameters using the genetic-algorithm variant of the LLS-SC procedure,²³⁹ with a population size of 400 and an evolution over 200 generations. The final (optimized) values of these parameters are reported in Table 2. The 10 types of Figure 1 are applied irrespective of the nature of the heavy atoms substituting the C–C bond (carbon or halogen).

Note that the above fitting of the torsions in the AA model is rather minimalistic in terms of the reference compounds selected (only one representative compound per torsion). Due to the absence of any torsional parameters appropriate for an AA model within the GROMOS force field, it is a prerequisite to making the present comparison between UA and AA models possible. Clearly, however, the construction of a full GROMOS AA force field (work in progress) will require a more thorough calibration of the torsions.

2.4. Force-Field Calibration Procedure

The parameterization procedure of the AA variant involved the following steps: (A) selection of initial parameters, (B) first optimization of the non-bonded interaction parameters for the ALK family, (C) optimization of the torsional and aliphatic-carbon third-neighbor interaction parameters for the ALK family, (D) second optimization of the non-bonded interaction parameters for the ALK family, (E) verification of the torsional profiles for the ALK family, and (F) optimization of the non-bonded interaction parameters specific to the HAL family. The selection of the initial parameters (A) is summarized in Supporting Information Section S.3 (Tables S.3 and S.4).

The optimization of the non-bonded interaction parameters (B, D, and F) followed the same principles as described in our previous article (see Section 2 in ref (157)). It relies on the minimization of an objective function Q(P; X^exp) of the parameter vector P which accounts for the deviation between the simulated-data vector X^sim(P) and the reference-data vector X^exp, that is, the values of ρ_liq and ΔH_vap for the calibration (CAL) sets (molecules and P,T-points). This objective function is defined as

1

where the index n corresponds to the N_n observable types and the index m corresponds to the N_m molecules in the family. The s_n coefficients eliminate the dependence on a unit system and adjust the relative weights of different observables in terms of perceived (i.e., subjective) extent of “badness”. They are set here to 20 kg m^–3 for ρ_liq and 1 kJ mol^–1 for ΔH_vap. The coefficients w_nm are set to one for all the combinations included (also considering observables at multiple state points).

During the optimization, the following steps are carried out over successive iterations i, starting from i = 0 and the associated initial vector of force-field parameters P₀^o: (1) perform simulations of all the systems to calculate the values of all the observables as well as their derivatives with respect to all the force-field parameters (sensitivity matrix); (2) calculate the real value Q_i of the objective function Q at iteration i; (3) minimize a linearized approximation 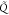to Q with respect to the parameters, starting from P_i^o and leading to P_i, using the information from the sensitivity matrix and restricting the search to a local trust region; (4) calculate the predicted value Q_i+1^pred of the objective function at P_i using the linearized approximation; and (5) set P_i+1^o to P_i, increment i, and iterate to step (1) until convergence. The purpose of the trust region is to limit the parameter changes in a given iteration to the region where the linearized approximation is expected to be valid. In practice, this restriction is introduced in the form of maximal allowed relative changes in all parameters (σ, ϵ, χ, and η) set to 5%.

The two optimization steps considering the ALK family (B and D) solely involved simulating the ALK-CAL molecules and performing changes in the force-field parameters relevant for the ALK family. Similarly, in the optimization for the HAL family (F), only the molecules of the HAL-CAL family were simulated, and only the parameters specific to the halogenated compounds were altered. Concerning the torsions (C and E), only one step (C) involves fitting against QM rotational profiles. The other step (E) only serves to validate the previously introduced torsional potentials.

2.5. Simulation and Analysis Protocols

The simulations were performed either using a home-developed GROMOS-compatible program in C++ called SAMOS or with the GROMOS program.^20,240−242 The SAMOS program was used for the iterative calibration of the non-bonded interaction parameters. The GROMOS program was used for the calculation of other liquid properties and solvation free energies.

The pure-liquid simulations relied on MD and were carried out under periodic boundary conditions based on cubic computational boxes containing 512 molecules. They were performed in the isothermal-isobaric ensemble at the reference pressures P and temperatures T listed in Supporting Information Section S.5 (Tables S.5 and S.6). Most simulations in the calibration sets of the ALK (71%) and HAL (70%) families were performed within at most 10 K from the standard temperature T^– = 298.15. The temperature in the remaining simulations ranged from 264 to 300 K (ALK) and from 220 to 405 K (HAL). Most simulations of the ALK-CAL (57%) and HAL-CAL (65%) sets were carried out within at most 0.2 bar from the standard pressure P° = 1 bar. The pressure in the remaining simulations ranged from 0.02 to 25.33 bar (ALK) and from 0.002 to 12.92 bar (HAL).

Besides the values of ρ_liq and ΔH_vap, 9 additional pure-liquid and solvation properties were calculated for assessing the relative accuracies of the UA and AA representations, considering the entire set of 591 molecules. These are the surface-tension coefficient γ, the isothermal compressibility κ_T, the isobaric thermal-expansion coefficient α_P, the isobaric heat capacity c_P, the static relative dielectric permittivity ϵ, the self-diffusion coefficient D, the shear viscosity η, the hydration free energy ΔG_wat, and the solvation free energy ΔG_che in cyclohexane.

The solvation free energies were calculated at P° = 1 bar and T^– = 298.15 K. The calculation of ΔG_wat relied on the SPC water model²³¹ and involved a computational box consisting of 1 solute molecule and 1000 water molecules. The calculation of ΔG_che relied on the 2016H66 cyclohexane UA model²² and involved 512 solvent molecules in the computational box. More information on the simulation and analysis protocols can be found in Supporting Information Section S.4.

3. Results and Discussion

3.1. Optimization of the Non-bonded Interaction Parameters

The evolution of the target function along the three non-bonded optimization phases of the AA force field for the ALK-CAL and HAL-CAL sets is shown in Figure 2. In the ALK-CAL case, two phases (before and after refinement of the torsional-dihedral potentials) are displayed on the same graph.

Figure 2.

Evolution of the predicted and real values of the objective function against the iteration number along the parameter optimization of the AA force field for the ALK-CAL (left) and HAL-CAL (right) sets. In the ALK-CAL case, two phases are displayed on the same graph (as indicated by the vertical dashed line). Iterations 1–3 are performed before the reoptimization of the dihedral potentials, and iterations 4–7 are performed after this reoptimization. For both sets, the first simulations at i = 0 using the initial parameter set (Supporting Information Section S.3) lead to a first real value Q₀^real and a first predicted value Q₁. The last simulations using the final (optimized) parameter set (Table 3) lead to the final real value of the objective function and a predicted value which is discarded.

For the ALK set, the real value of the target function drops sharply from 0.82 to 0.55 over the first three iterations. Using the parameters at iteration 3, the torsional and aliphatic-carbon third-neighbor interaction terms are refined. The second optimization from iteration 4 until 7 brings a slight further improvement, with a final value of 0.47. Similarly, in the subsequent calibration of the HAL set, the target function decreases sharply over the first two iterations and converges to 1.31 after seven iterations.

The comparison between experimental values and simulation results for ρ_liq and ΔH_vap considering both the UA and AA force-field variants is shown in Figure 3, and the corresponding numerical values can be found in Supporting Information Section S.5. The associated statistics in terms of root-mean-square deviation (RMSD) and average deviation (AVED) is provided in Table 4.

Figure 3.

Comparison between experimental values and simulation results for ρ_liq and ΔH_vap considering the calibration and validation sets based on the optimized force field in its UA and AA variants. The comparison is shown for the liquid density ρ_liq (left) and for the vaporization enthalpy ΔH_vap (right), considering the ALK (top) and HAL (bottom) families. Symbols are used to distinguish the CAL (plus symbol) and VAL (bullet symbol) sets. Colors are used to distinguish the UA (blue) and AA (red) force-field variants. The diagonal solid lines indicate perfect agreement, and the range between the two dashed lines indicates agreement within ±40.0 kg m^–3 for ρ_liq or ±2.0 kJ mol^–1 for ΔH_vap. The corresponding numerical values can be found in Supporting Information Tables S.5 and S.6, and the statistics per groups of compounds are listed in Table 4. The same graphs restricted to the CAL and VAL sets only are shown in Supporting Information Section S.6 (Figures S.5 and S.6).

Table 4. Statistics Concerning the Discrepancies between Experimental Values and Simulation Results for ρ_liq and ΔH_vap Considering the Calibration and Validation Sets Based on the Optimized Force Field in Its UA and AA Variants^a.

	ρliq [kg m−3]					ΔHvap [kJ mol−1]
		RMSD		AVED			RMSD		AVED
group	N	UA	AA	UA	AA	N	UA	AA	UA	AA
	Calibration
ALK	14	8.6	13.8	–1.1	2.0	11	1.0	0.6	–0.7	0.1
HAL	190	36.5	33.0	3.5	–1.9	132	2.5	2.5	–0.1	–0.1
F	30	48.2	38.7	–27.1	–25.9	24	2.3	2.3	–1.1	–0.4
Cl	47	15.7	13.6	0.7	2.3	40	2.4	1.7	–0.1	–0.2
Br	44	29.2	33.6	4.6	0.5	35	2.5	2.2	–0.0	–0.0
I	31	51.6	49.6	33.3	9.5	11	1.1	2.7	–0.9	–1.3
Y	38	36.9	26.8	5.5	–0.3	22	3.5	3.7	1.2	1.0
ALL	204	35.3	32.0	3.2	–1.6	143	2.4	2.4	–0.2	–0.1
	Validation
ALK	137	14.0	13.0	11.2	10.6	137	1.1	2.1	0.7	1.9
HAL	241	27.6	34.3	5.3	16.6	99	1.8	2.1	–0.0	0.5
F	18	27.4	25.8	–5.9	1.5	16	1.8	1.7	–0.1	–0.4
Cl	105	19.6	24.9	4.5	10.5	42	1.5	1.9	0.0	0.8
Br	81	28.5	33.9	3.3	20.8	32	2.2	2.4	–0.2	0.2
I	30	24.8	41.1	18.4	36.9	9	1.6	2.1	0.1	1.1
Y	7	81.0	95.2	15.1	11.9	0
ALL	378	23.6	28.5	7.4	14.4	236	1.4	2.1	0.4	1.3

^aFor selected groups, the number N of experimental data points, the root-mean-square deviation (RMSD) and the average deviation (AVED) are reported for the pure-liquid density ρ_liq and the vaporization enthalpy ΔH_vap. The group codes are alkanes (ALK), haloalkanes (HAL), homo-fluorinated (F), homo-chlorinated (Cl), homo-brominated (Br), homo-iodinated (I), and hetero-haloalkane (Y).

For the CAL sets, the simulation results are in excellent agreement with the reference experimental data for ρ_liq, with RMSD values of 8.6 and 13.8 kg m^–3 for the UA-ALK and AA-ALK sets, respectively, and of 36.5 and 33.0 kg m^–3 for the UA-HAL and AA-HAL sets, respectively. The same holds for ΔH_vap, with RMSD values of 1.0 and 0.6 kJ mol^–1 for the UA-ALK and AA-ALK sets, respectively, and of 2.5 and 2.5 kJ mol^–1 for the UA-HAL and AA-HAL sets, respectively. The small differences between the UA and AA representations are not significant, and the models at the two different resolutions essentially present the same accuracy for the CAL sets at full optimization.

For the VAL sets, the two levels of resolution also perform comparably well in terms of ρ_liq, with RMSD values of 14.0 and 13.0 kg m^–3 for the UA-ALK and AA-ALK sets, respectively, and of 27.6 and 34.3 kg m^–3 for the UA-HAL and AA-HAL sets, respectively. However, the difference in terms of ΔH_vap is more significant, with RMSD values of 1.1 and 2.1 kJ mol^–1 for the UA-ALK and AA-ALK sets, respectively, and of 1.8 and 2.1 kJ mol^–1 for the UA-HAL and AA-HAL sets, respectively. Here, the UA variant is noticeably more accurate, especially for the alkanes. The larger deviation in ΔH_vap for the AA variant is predominantly due to an overestimation for long alkane molecules. In particular, 22 alkane compounds with 8–10 carbon atoms show positive deviations in ΔH_vap that are larger than 2.5 kJ mol^–1 (k_BT at room temperature). These molecules are shown in Supporting Information Section S.7 (Figure S.7), and all correspond to branched alkanes with buried ternary or quaternary carbon atoms.

For the ALK family, the graphs of ρ_liq and ΔH_vap both present positive deviations that increase in magnitude with the quantity itself. The reason is that the representative points for the CAL set (11 lightest alkanes, excepting methane and ethane) and the VAL set (137 larger alkanes) cover different regions of the graphs (lower ρ_liq and ΔH_vap values for CAL as opposed to VAL). While the AVED values are close to 0 for the CAL set, they are systematically positive and generally much larger in magnitude (factor 5–20) for the VAL set (except ΔH_vap for the UA model, where the magnitude is the same). As explained in Section 2.2, the LJ parameters of the aliphatic (non-halogenated) UAs were left unchanged upon optimization of the UA force field in ref (157). The overestimation of ρ_liq for the VAL set of the ALK family thus results from a slight deficiency of the standard GROMOS force field for alkanes in terms of the liquid density of higher alkanes. For the AA model, the overestimation of both ρ_liq and ΔH_vap for the VAL set is likely to result from the simultaneous fitting of the ALK and HAL families. Although the halogenated and non-halogenated carbon atom types are kept distinct in the AA model, they are simultaneously present in the HAL compounds, which induces a correlation in the corresponding parameters. Since the simultaneous calibration involves CAL sets that are larger for the HAL compared to the ALK family (137 vs 11 molecules), this results in a lower accuracy for the ALK family.

3.2. Optimized Torsional Parameters

The comparison between the rotational energy profiles in vacuum for the 10 relevant dihedral angles of alkane molecules (Figure 1), calculated using either QM or the optimized force-field parameters at the UA or AA levels, is shown in Figure 4.

Figure 4.

Rotational energy profiles of the saturated alkanes in vacuum. The dihedral angles considered are shown in Figure 1, and the corresponding representative molecules are ethane (A2001), propane (A3001), 2-methylpropane (A4001), 2,2-dimethylpropane (A5001), butane (A4002), 2-methylbutane (A5002), 2,2-dimethylbutane (A6001), 2,3-dimethylbutane (A6002), 2,2,3-trimethylbutane (A7001), and 2,2,3,3-tetramethylbutane (A8001), respectively, for the dihedrals (a–j). The energies correspond to minimized structures, and all profiles are anchored to zero at their global minimum. During the minimization of a given dihedral angle, the other dihedral angles were constrained to a fixed value corresponding to the trans conformation. The QM profiles correspond to the MP2 level of theory²³⁵ using a 6-311G(dp) basis set²³⁶ for the structure optimization and an aug-cc-pVTZ basis set^237,238 for the energy calculation.

At the AA level, all profiles achieve excellent agreement with the QM results. The RMSD between the QM and AA energies over the 36 sampled dihedral-angle values never exceeds 1.1 kJ mol^–1. At the UA level, which relies on a single common type for all the alkane molecules, and for which the torsional parameters have not been reoptimized, the agreement is somewhat less good. For the dihedral angles (e) and (f), the RMSD is about 2.7 kJ mol^–1. For the types (i) and (j), which involve more highly substituted carbon atoms, the RMSD values are 5.7 and 12.1 kJ mol^–1, respectively. Note, however, that these discrepancies mainly affect the barrier heights and not the relative energies of the conformers.

3.3. Optimized Non-Bonded Interaction Parameters

The final values of the non-bonded interaction parameters for the AA variant are reported in Table 3. The corresponding values for the UA variant can be found in ref (157) (see Table 3 therein). The parameters for the carbon, hydrogen, and halogen atom types in the two variants are compared graphically in Figure 5. The aliphatic and halogenated (united-)atom types of the UA variant are not included.

Figure 5.

Comparison of the non-bonded interaction parameters of the optimized force field in its AA and UA variants. The values are shown for the LJ collision diameter σ and well depth ϵ as well as the EE hardness η and electronegativity χ. The values for the carbon, hydrogen, and halogen atom types are shown in both variants. The aliphatic and halogenated (united-)atom types of the UA variant are not included. For the elements C and H, the types C and H are shown in magenta and the types CX and HX are shown in blue. For the halogen elements, the types corresponding to the UA variant are shown in green and those for the AA variant are shown in red. The shorter bar is always shown in front of the larger one (so that the lengths of both are visible). The values are reported numerically in Table 3 for the AA variant. The corresponding values for the UA variant can be found in ref (157) (see Table 3 therein).

Considering the halogen atoms, the AA and UA parameters do not differ dramatically. These atoms have slightly higher σ and lower ϵ in the AA variant. The χ values are very similar, while η in the AA model is lower for F and higher for Cl, Br, and I. In both variants, the four non-bonded interaction parameters in the optimized force field show trends along the halogen series that are consistent with chemical intuition. The LJ parameters σ and ϵ both increase along the series, in line with an increase in atomic size and electronic polarizability. The EE parameters η and χ generally decrease along the series, in line with a decrease of the electronegativity and an increase of the softness, except for an inversion in terms of η between Br and I in the AA model.

Considering the elements carbon and hydrogen in the AA model, one may compare the types C and H relevant for alkanes to the types CX and HX relevant for haloalkanes. The corresponding σ and ϵ values are similar. However, CX and HX present a higher η and a lower χ compared to C and H. This suggests that these atom types have distinct properties and should indeed be kept separate to ensure an accurate reproduction of the electrostatic properties by the force field.

Note also that the σ values for carbon in the AA representation (0.31 nm for CX or 0.33 nm for CH) are significantly lower than the corresponding values for the carbon UAs CH0–CH3 in the UA variant (between 0.38 and 0.66 nm), see Table 3 in ref (157). This is expected considering that the explicit hydrogen atoms in the AA model protrude outside the envelope of the carbon atom.

The atomic partial charges involved in the charge groups relevant for saturated alkanes in the AA variant are shown in Figure 6. A corresponding illustration for the charge groups of the saturated homo-haloalkanes is provided in Figure 7, with the associated charges reported in Table 5.

Figure 6.

Charge groups and atomic partial charges on the carbon (black) and hydrogen (red) atoms within the five charge groups for alkane molecules in the AA variant. Only hydrogen atoms are shown explicitly (the atoms connected by lines are carbon atoms). The charges are in units of the elementary charge e.

Figure 7.

Charge groups for haloalkane molecules in the AA variant. The atomic partial charges for the homo-haloalkane charge groups are reported in Table 5. Only hydrogen and halogen atoms are shown explicitly (the atoms connected by lines are carbon atoms).

Table 5. Charges on the Halogen, Hydrogen, and Carbon Atoms in the Six Homo-Halogenated Charge Groups of the Force Fields for the Haloalkanes in Either the UA (Top) or AA (Bottom) Variants^a.

	type	F	H	C	Cl	H	C	Br	H	C	I	H	C
	[e]
(a)	CH2X1	–0.302		0.302	–0.270		0.270	–0.236		0.236	–0.202		0.202
(b)	CH1X1	–0.328		0.328	–0.304		0.304	–0.270		0.270	–0.239		0.239
(c)	CH1X2	–0.282		0.564	–0.250		0.500	–0.219		0.438	–0.189		0.378
(d)	CH0X1	–0.331		0.331	–0.310		0.310	–0.276		0.276	–0.245		0.245
(e)	CH0X2	–0.289		0.578	–0.260		0.520	–0.229		0.458	–0.199		0.398
(f)	CH0X3	–0.257		0.771	–0.224		0.672	–0.196		0.588	–0.167		0.501
(a)	CH2X1	–0.260	0.108	0.044	–0.194	0.090	0.014	–0.148	0.077	–0.006	–0.114	0.068	–0.022
(b)	CH1X1	–0.229	0.138	0.091	–0.165	0.114	0.051	–0.121	0.097	0.024	–0.092	0.086	0.006
(c)	CH1X2	–0.177	0.186	0.168	–0.125	0.146	0.104	–0.090	0.120	0.060	–0.070	0.104	0.036
(d)	CH0X1	–0.173		0.173	–0.116		0.116	–0.077		0.077	–0.055		0.055
(e)	CH0X2	–0.123		0.246	–0.081		0.162	–0.053		0.106	–0.039		0.078
(f)	CH0X3	–0.095		0.285	–0.062		0.186	–0.040		0.120	–0.030		0.090

^aThese charge groups are depicted in Figure 7, where all the halogen sites (X) are substituted by the same type of halogen atom. The charges are in units of the elementary charge e.

For the alkanes, the charge on the explicit hydrogen atoms becomes less positive when the number of hydrogen atoms in the charge group increases from one (methanetriyl group) to two (methylene group) and then to three (methyl group), showing that the non-additivity of induction effects can be accounted for by the EE scheme. Note, however, that the magnitudes of the charges on the hydrogen atoms are significantly larger here than in other AA force fields with fixed hydrogen partial charge, for example 0.00, 0.06, and 0.09 e for MMFF94,²⁴³ OPLS-AA,²⁴ and CHARMM94,²⁵ respectively.

For the haloalkanes, the trends are similar to those previously observed for the UA representation.¹⁵⁷ The substitution of hydrogen atoms by electron-donating (hyperconjugative) alkyl groups tends to enhance the polarization of the carbon-halogen bond, whereas the substitution of hydrogen or carbon atoms by electron-withdrawing halogen atoms inhibits this polarization.

3.4. Pure-Liquid and Solvation Properties

The comparison between experimental values and simulation results concerning additional thermodynamic, transport, dielectric, and solvation properties is shown in Figure 8. This figure considers the results obtained for the entire ALK and HAL families (including both CAL and VAL sets) using either the AA or UA representation (see also Figure 3 for the comparison involving ρ_liq and ΔH_vap). The corresponding numerical values can be found in Supporting Information Section S.5, and the statistics in terms of RMSD and AVED (also including ρ_liq and ΔH_vap) is reported in Table 6. In terms of overall RMSD and considering the 11 properties, the UA representation is systematically more accurate except for η. However, the difference in accuracy is not very pronounced, except for c_P and ΔG_wat, where the UA variant performs significantly better.

Figure 8.

Comparison between experimental values and simulation results concerning additional thermodynamic, transport, dielectric, and solvation properties, and considering the optimized force field in its UA and AA variants. The properties presented are the surface-tension coefficient γ, the isothermal compressibility κ_T, the isobaric thermal-expansion coefficient α_P, the isobaric heat capacity c_P, the self-diffusion coefficient D, the shear viscosity η, the static relative dielectric permittivity ϵ, the hydration free energy ΔG_wat, and the solvation free energy ΔG_che in cyclohexane. The comparison is shown for the ALK molecules (including both CAL and VAL sets) using either AA (AA-ALK) or UA (UA-ALK; reported from ref (157)) and the HAL molecules (including both CAL and VAL sets) using either AA (AA-HAL) or UA (UA-HAL; reported from ref (157)). See also Figure 3 for ρ_liq and ΔH_vap. The corresponding numerical values can be found in Supporting Information Section S.5, and the statistics in terms of RMSD and AVED is reported in Table 6. The result for the molecule I6202 was omitted from the η plot (too large deviation).

Table 6. Statistics Concerning the Discrepancies between Experimental Values and Simulation Results for the UA and AA Variants Considering the Entire Set (ALL) and Different Subsets of Molecules^a.

		RMSD		AVED			RMSD		AVED			RMSD		AVED
		UA	AA	UA	AA		UA	AA	UA	AA		UA	AA	UA	AA
group	N	ρliq [kg m–3]				N	ΔHvap [kJ mol–1]				N	γ [mN m–1]
ALK	151	13.5	13.1	10.0	9.8	148	1.1	2.0	0.6	1.8	54	0.9	3.8	0.6	–3.8
HAL	431	31.9	33.8	4.5	8.4	231	2.2	2.3	–0.1	0.1	72	2.6	5.3	–1.6	–4.9
F	48	41.6	34.5	–19.2	–15.6	40	2.1	2.1	–0.7	–0.4	9	0.9	4.1	–0.1	–4.0
Cl	152	18.5	22.1	3.3	8.0	82	2.0	1.8	–0.1	0.3	25	2.2	5.3	–2.0	–5.2
Br	125	28.8	33.8	3.7	13.7	67	2.3	2.3	–0.1	0.1	23	2.2	5.6	–1.9	–5.4
I	61	40.6	45.6	26.0	23.0	20	1.3	2.4	–0.4	–0.2	12	3.1	5.7	–2.8	–5.5
Y	45	46.6	44.9	7.0	1.6	22	3.5	3.7	1.2	1.0	3	6.9	5.5	3.2	1.8
ALL	45	28.3	29.8	6.0	8.8	22	1.9	2.2	0.2	0.8	3	2.1	4.7	–0.7	–4.4
		κT [10–5 bar–1]					αP [10–4 K–1]					cP [J K–1 mol–1]
ALK	13	1.2	3.7	–0.4	2.1	146	0.8	3.1	–0.7	2.9	20	56.5	231.0	–54.8	225.0
HAL	15	2.1	2.9	1.2	2.0	313	1.7	2.9	–0.3	2.2	65	37.5	162.8	–34.8	143.7
F	0					20	5.6	6.8	–1.8	3.8	2	32.8	226.8	–25.2	194.9
Cl	6	2.5	3.7	1.9	3.2	131	1.0	2.5	–0.3	2.2	25	36.4	163.0	–33.7	142.9
Br	5	2.0	2.5	1.0	1.8	89	0.8	1.7	–0.4	1.6	22	41.8	182.6	–40.4	166.5
I	4	1.6	2.0	0.3	0.4	54	0.6	2.3	0.5	2.3	10	39.3	136.7	–38.5	128.3
Y	0					19	1.2	3.6	0.6	3.1	6	20.2	76.3	–15.7	72.4
ALL	4	1.7	3.3	0.5	2.0	19	1.4	2.9	–0.4	2.4	6	42.8	181.2	–39.5	162.9
		ϵ					D [109 m–2 s–1]					η [mPa s]
ALK	43	0.9	0.7	–0.9	–0.7	15	0.7	0.9	0.5	–0.9	33	0.2	0.1	–0.1	0.1
HAL	93	3.1	4.2	–2.6	–3.8	8	0.7	0.5	0.6	0.2	45	1.0	0.7	–0.5	–0.3
F	4	6.8	6.4	–5.0	–3.9	0					4	0.1	0.0	–0.1	–0.0
Cl	35	2.9	4.2	–2.4	–3.8	3	1.0	0.7	1.0	0.6	21	0.4	0.2	–0.3	–0.1
Br	37	2.7	4.0	–2.4	–3.7	4	0.4	0.4	0.4	–0.0	12	0.8	0.5	–0.5	–0.3
I	13	2.2	3.7	–2.1	–3.5	1	0.6	0.1	0.6	–0.1	8	2.0	1.4	–1.2	–0.6
Y	4	5.4	5.9	–5.3	–5.9	0					0
ALL	4	2.7	3.5	–2.1	–2.8	1	0.7	0.8	0.6	–0.5	8	0.8	0.5	–0.3	–0.1
		ΔGwat [kJ mol–1]					ΔGche [kJ mol–1]
ALK	24	1.9	4.1	–1.4	–3.3	26	2.5	4.6	–1.8	–4.0
HAL	42	2.0	9.7	1.2	–8.2	29	5.2	5.7	–4.4	–5.1
F	4	4.2	8.3	3.7	–7.1	3	2.7	3.5	–1.7	–2.3
Cl	18	1.6	9.1	0.7	–7.5	14	3.9	4.7	–3.1	–4.1
Br	11	1.8	10.4	1.4	–8.5	8	6.1	6.5	–5.9	–6.3
I	7	1.0	11.5	1.0	–10.7	4	8.1	8.1	–8.1	–8.0
Y	2	1.4	6.8	1.0	–6.7	0
ALL	2	2.0	8.1	0.3	–6.4	4	4.2	5.2	–3.2	–4.6

^aThese subsets are alkanes (ALK), haloalkanes (HAL), and subsets of haloalkanes: homo-fluorinated (F), homo-chlorinated (Cl), homo-brominated (Br), homo-iodinated (I), and hetero-haloalkane (Y). They include both calibration and validation molecules. The number of observables (N), along with the root-mean-square deviation (RMSD) and the average deviation (AVED), are reported. The properties considered are the pure-liquid density ρ_liq, the vaporization enthalpy ΔH_vap, the surface-tension coefficient γ, the isothermal compressibility κ_T, the isobaric thermal-expansion coefficient α_P, the isobaric heat capacity c_P, the self-diffusion coefficient D, the shear viscosity η, the static relative dielectric permittivity ϵ, the hydration free energy ΔG_wat, and the solvation free energy ΔG_che in cyclohexane. The corresponding correlations are shown graphically in Figures 3 and 8.

A good agreement with experimental data is observed for the surface-tension coefficient γ, with RMSD values of 2.1 mN m^–1 for UA and 4.7 mN m^–1 for AA. This is not surprising considering that γ probes the cohesive intermolecular forces within the liquid and is thus highly correlated with ΔH_vap (see refs (22, 119, 169, and 174)), which is a parameterization target. The AA representation is associated with a higher and systematic error relative to experiment (AVED of −4.4 mN m^–1) compared to the UA representation, which is in line with the higher residual deviations observed in terms of ΔH_vap. Note that the inclusion of long-range dispersion (via either a lattice-sum or a tail-correction approach) would likely increase the surface-tension coefficient,¹¹⁹ improving the agreement with experiment for the AA but not for the UA model. However, the force fields should then also be calibrated using such a correction (resulting in different optimal parameters). Note also that the inclusion of a long-range dispersion would be inconsistent with the current parameterization settings of the GROMOS force-field family.

In terms of the isothermal compressibility κ_T, both representations perform comparably well, with RMSD values of 1.7 × 10^–5 bar^–1 for UA and 3.3 × 10^–5 bar^–1 for AA. These errors are in line with those reported in ref (174) for the OPLS-AA and AMBER-GAFF force fields, and in ref (22) for the 2016H66 force field (RMSD values of 2.8–3.0 × 10^–5 bar^–1). Considering that the balance between density and compressibility in a simulated liquid is largely related to the functional form selected for the repulsive component of the van der Waals interactions, the good agreement observed here for both ρ_liq and κ_T suggests that the inverse-twelfth-power form used in the short-range LJ repulsion²²⁵ is adequate in this context.²²

For the thermal-expansion coefficient α_P, the agreement between simulation and experiment is also good for both representations, with RMSD values of 1.4 × 10^–4 K^–1 for UA and 2.9 × 10^–5 K^–1 for AA. These deviations are comparable to the ones reported in refs (22 and 174) (RMSD values between 3.0 and 4.4 × 10^–4 K^–1). The results for the UA model are closer to the experimental values, while the AA results tend to be slightly overestimated (AVED of 2.4 × 10^–4 K^–1). This error increases with the size of the molecule, leading to a correlation slope of 1.2 (compared to 0.9 for the UA model). Because α_P characterizes a temperature derivative (that of the volume), this slight difference might be a reflection of the different accuracies with which the heat capacity is reproduced by the two models (see below).

Regarding the isobaric heat capacity c_P, the RMSD values are 42.8 J K^–1 mol^–1 for UA and 181.2 J K^–1 mol^–1 for AA. Here, the UA representation delivers somewhat underestimated values (AVED of −39.5 J K^–1 mol^–1), and the AA representation delivers largely overestimated values (AVED of 162.9 J K^–1 mol^–1). These errors are roughly proportional to the size of the molecule, which leads to correlation lines with approximate slopes equal to 2.2 for the UA model and 0.95 for the AA model (instead of one for perfect agreement). It is interesting to compare the present observations to those of ref (22) (see Figure 3 therein) and ref (174) (see Figure 7 therein), which show very similar features for the UA force field GROMOS-2016H66 compared to the AA force fields AMBER-GAFF and OPLS-AA. In practice, the accuracy of a classical model in terms of reproducing heat capacities will always remain limited because (i) a number of vibrational modes are not (or only partly) excited quantum-mechanically even at room temperature, especially those involving stiff degrees of freedom and light atoms, and (ii) a number of degrees of freedom may (or not) be included in the classical model (e.g., flexible or constrained bonds, inclusion or exclusion of aliphatic hydrogen atoms). As explained in ref (22), using UAs implicitly eliminates the contribution of high-frequency vibrations involving the aliphatic hydrogens, leading to more realistic classical c_P estimates. These discrepancies at the AA level can be at least partly remedied by applying quantum corrections to the results calculated at the classical level.^{174,204−206} However, since the classical (uncorrected) c_P value still determines the temperature derivatives of the thermodynamic properties within the force field, the better agreement of the UA variant with experiment suggests a better transferability of this variant across temperature, compared to the AA variant.

For the dielectric permittivity ϵ, the agreement between calculated and experimental values is reasonable, with RMSD values of 2.7 for UA and 3.5 for AA. For the ALK family, the representative points for all the compounds are almost at the same locations on the graph. In the UA representation, the calculated value is always 1 due to the absence of partial charges. This is lower than the typical experimental value of about 1.9 for alkanes, leading to an AVED of −0.9 (systematic, thus an RMSD of 0.9). In the AA model, the calculated permittivities now slightly differ from 1 (on the order of 1.2), and the AVED becomes −0.7 (RMSD very close to 0.7). For the HAL family, both the UA and AA results are systematically somewhat underestimated, more pronouncedly so in the AA representation. For qualitative comparison, the results obtained here give an RMSD on the same order as the AMBER-GAFF, OPLS-AA, and 2016H66 force fields (7.6–15.9).^22,174

In terms of the transport properties D and η, small but systematic differences are observed between the UA and AA variants. For D, the RMSD values are 0.7 × 10⁹ m² s^–1 for UA and 0.8 × 10⁹ m² s^–1 for AA. For η, the RMSD values are 0.8 mPa s for UA and 0.5 mPa s for AA. In the UA representation, D is overestimated and η underestimated, whereas in the AA representation, both properties are slightly underestimated. The observation of anti-correlated trends in the two quantities is not unexpected based on the Stokes–Einstein–Sutherland equation,^244,245 suggesting that D and η should be approximately inversely related for a given molecule size and temperature. The diffusivity enhancement in the UA model is due to the omission of the explicit hydrogen atoms, resulting in smoother intermolecular interactions.^201−203

Regarding the hydration free energy ΔG_wat, the UA variant results in a much better agreement with the experimental data, with an RMSD value of 2.0 kJ mol^–1 for UA compared to 8.1 kJ mol^–1 for AA. For the ALK molecules in the UA representation, the parameters are unchanged from those of the GROMOS alkane force field. They have been shown²³⁴ to reproduce extremely well the experimental values for ΔG_wat when using the SPC model,²³¹ without any adjustment (e.g., bypass of the combination rule) for the alkane–water interactions.

The same observation holds for the HAL family at the UA resolution, for which the calculated ΔG_wat values are accurate as well. In contrast, the AA model does not benefit from such a (fortuitous) compatibility with the SPC model. This leads to a large and systematic negative error in the calculated hydration free energies, that is, an overhydration of the molecules. This effect is probably in part caused by the relatively large hydrogen charges in the present case compared to other AA force fields. This issue will have to be remedied in future work, likely by enhancing the repulsive LJ parameters between aliphatic carbon and/or hydrogen atoms and water molecules, via a by-passing of the corresponding combination rule.

In terms of the solvation free energy ΔG_che in cyclohexane, there is much less difference between the UA and AA representations, with RMSD values of 4.2 kJ mol^–1 for UA and 5.2 kJ mol^–1 for AA. The agreement is reasonable for both representations, with a slight general trend toward negative deviations, that is, an oversolvation of the molecules, somewhat more pronounced in the AA representation. The deviations are tendentially more pronounced for haloalkanes containing bromine or iodine atoms in both representations. The better agreement of the ΔG_che results compared to the ΔG_wat ones is likely related to the fact that aliphatic–aliphatic interactions are considered during the calibration, but not aliphatic–water ones. Note that in the context of the AA model, the solute–solvent interactions are a mix between AA (solute) and UA (cyclohexane) resolutions, which may explain the slightly larger deviations in terms of ΔG_che.

4. Conclusions

Ideally, to assess in a fair way the effect of a specific FFV on the intrinsic accuracy of the classical force-field representation, one has to perform a comparison where (i) only the specific FFV change is considered and (ii) the comparison is performed at an optimal level of parameterization relative to a given set of training molecules, monitored observables, and target values.

This work aimed at performing such a comparison in one specific case of FFV, namely the choice of a UA or an AA resolution within GROMOS-based settings for the functional-form and simulation-parameter choices. The comparison relied on 591 saturated acyclic (halo)alkane molecules with 1 to 10 carbon atoms as a training set, the pure-liquid density ρ_liq and vaporization enthalpy ΔH_vap as the monitored observables, and 961 experimental values for these properties as the target data. The two force fields were optimized automatically using the CombiFF approach.^157,158 For the AA force field, the parameterization also involved a refinement of the torsional-energy terms and third-neighbor LJ interaction parameters against QM rotational-energy profiles. The comparison between the UA and AA resolutions was then extended to properties that were not included as parameterization targets.

It should be stressed that the force fields optimized using CombiFF generally do not represent unique solutions. Previous work involving multiple optimizations initiated from different starting parameters (see ref (157) for the HAL family, Supporting Information Section S.8 therein; similar observations were made subsequently for the O + N family of ref (158)) have shown that (i) different solutions of similar accuracies are obtained and (ii) the corresponding EE parameters evidence significant variations, while the LJ parameters and EE-derived partial charges are more similar. The UA and AA force-field variants derived here are thus probably close to optimality but not unique. Considering a limited calibration set, the simpler UA model is expected to be less affected by this degeneracy compared to the AA model. This may in part explain the slightly higher transferability of the UA compared to the AA model toward the validation set.

In terms of the target properties ρ_liq and ΔH_vap, there is no significant difference in the accuracy levels reached by the UA and AA representations within optimized force fields. The only noticeable difference is a slightly better performance of the UA model for ΔH_vap in the context of the branched alkane molecules with 8–10 carbon atoms. This is in line with the observations made in a number of previous studies,^{47−55,174,181−183,208−210} suggesting that in terms of bulk thermodynamic properties, there is no systematic and significant accuracy gain upon changing from the UA to the AA resolution, and the main differences observed stem rather from a possible (sub)optimality of one or the other parameterization.

Note, however, that the absolute ideal of an optimal parameterization level is not yet entirely reached in the present study.

First, several parameters were not subjected to optimization. These include the bond-stretching and bond-angle bending parameters, the torsional and third-neighbor parameters (or a subset thereof for the AA model), and the aliphatic (united-)atom non-bonded parameters (for the UA model). Since the condensed-phase thermodynamic properties of small organic molecules depend primarily on intermolecular packing and energetics, they are expected to be most sensitive to the non-bonded interaction parameters. While bond-stretching and bond-angle bending parameters play a marginal role (slight modulation of the molecular geometry), torsional parameters are likely more important (through their influence on the molecular conformation). For this reason, they are partly reoptimized in the AA model, while their values in the UA model (as those of the aliphatic non-bonded parameters in this model) have been optimized very carefully in previous work.^233,234,246 The present results are thus expected to be relatively insensitive to the values of the non-optimized parameters and/or the values retained for these parameters to be already close to optimal. Nevertheless, this still leaves room for a small extent of suboptimality in the derived force fields.

Second, the optimization was limited by the selection of specific atom types. This can be illustrated by a simple thought experiment. From the intermolecular-interaction perspective, an AA model for alkanes where the hydrogen atoms would be kept uncharged and exempt of LJ interactions, and the carbon-atom volumes would be appropriately expanded, could become a UA model. Thus, in principle, an AA model of alkanes must be at least as accurate as a UA model because it admits this model as a limiting case while having more fitting parameters. In the present AA optimization, however, the AA force field could not reach this limiting UA case due to the use of a single carbon atom type for all aliphatic groups.

Even if it remains somewhat imperfect, the use of CombiFF takes us much closer to performing a comparison at an optimal parameterization level compared to a heuristic calibration approach. The effect of including the covalent terms and UA aliphatic parameters in the calibration, as well as of considering an AA model with separate aliphatic-carbon atom types, will be investigated in future work.

Even though the UA and AA resolutions perform similarly well concerning the calibration targets ρ_liq and ΔH_vap, there may be more pronounced differences in their relative accuracies for non-target thermodynamic, dielectric, transport, and solvation properties. Concerning the nine additional properties monitored here, the AA representation leads to more accurate results in terms of η; comparably accurate results in terms of γ, κ_T, α_P, ϵ, D, and ΔG_che; and less noticeably accurate results in terms of c_P and ΔG_wat. The artificially enhanced diffusivity in the UA model is due to the omission of explicit hydrogen atoms, resulting in smoother intermolecular interactions,^201−203 and the artificially increased heat capacity in the AA model is due to the classical treatment of the vibrations involving the hydrogen atoms.^{22,174,204−206} Concerning ΔG_wat, the better performance of the UA model is probably in part coincidental, that is, it appears that the UA model is directly compatible with the SPC water model given the applied geometric-mean combination rule.²³⁴ This does not hold for the AA model, where the solute molecules are oversolvated in water. This effect is probably partly caused by the relatively large hydrogen charges (0.157–0.303 e for the aliphatic groups) compared to other AA force fields, for example, 0.00, 0.06, and 0.09 e for MMFF94,²⁴³ OPLS-AA,²⁴ and CHARMM94,²⁵ respectively. This issue will have to be remedied in future work, likely by enhancing the repulsive LJ parameters between aliphatic carbon and/or hydrogen atoms and water molecules via a by-passing of the corresponding combination rule. Note, finally, that structural observables are still missing in the present comparison. In particular, the explicit hydrogen representation in the AA model could be required for the representation of directional interactions (carbon-bound hydrogen as a weak hydrogen-bond donor), which may be important in the context of drug design.

Future work will involve the assessment of other FFVs in classical force fields and in particular (i) a change in the cutoff distance, (ii) the use of an alternative functional form for the van der Waals repulsion, (iii) the possible inclusion of a long-range LJ correction, and (iv) a change of the combination rules. Finally, besides the UA versus AA comparison, this work also represents a first step toward the calibration of a GROMOS-compatible force field at the AA resolution.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.2c00524.

• Detailed information concerning the molecules considered in this work; the reference experimental data; the initial values of the parameters; the details on simulation and analysis protocols; the comparison between experimental and calculated properties; variants of Figure 3 restricted to the CAL and VAL sets; and structures of alkanes with deviations larger than 2.5 kJ mol^–1 for ΔH_vap (PDF)

The authors declare no competing financial interest.