Abstract
We present a biologically inspired recurrent neural network (RNN) that efficiently detects changes in natural images. The model features sparse, topographic connectivity (st-RNN), closely modeled on the circuit architecture of a “midbrain attention network.” We deployed the st-RNN in a challenging change blindness task, in which changes must be detected in a discontinuous sequence of images. Compared with a conventional RNN, the st-RNN learned 9x faster and achieved state-of-the-art performance with 15x fewer connections. An analysis of low-dimensional dynamics revealed putative circuit mechanisms, including a critical role for a global inhibitory (GI) motif, for successful change detection. The model reproduced key experimental phenomena, including midbrain neurons' sensitivity to dynamic stimuli, neural signatures of stimulus competition, as well as hallmark behavioral effects of midbrain microstimulation. Finally, the model accurately predicted human gaze fixations in a change blindness experiment, surpassing state-of-the-art saliency-based methods. The st-RNN provides a novel deep learning model for linking neural computations underlying change detection with psychophysical mechanisms.
SIGNIFICANCE STATEMENT For adaptive survival, our brains must be able to accurately and rapidly detect changing aspects of our visual world. We present a novel deep learning model, a sparse, topographic recurrent neural network (st-RNN), that mimics the neuroanatomy of an evolutionarily conserved “midbrain attention network.” The st-RNN achieved robust change detection in challenging change blindness tasks, outperforming conventional RNN architectures. The model also reproduced hallmark experimental phenomena, both neural and behavioral, reported in seminal midbrain studies. Lastly, the st-RNN outperformed state-of-the-art models at predicting human gaze fixations in a laboratory change blindness experiment. Our deep learning model may provide important clues about key mechanisms by which the brain efficiently detects changes.
Keywords: change blindness, deep learning, global inhibition, midbrain attention network, saliency map, superior colliculus
Introduction
Detecting critical changes in the environment is essential for adaptive survival. Forebrain regions in the prefrontal and parietal cortex, and the medial temporal lobe are all known to be involved in change detection (Beck et al., 2001; Pessoa and Ungerleider, 2004; Reddy et al., 2006). In comparison, the role of the midbrain in change detection is relatively unknown. Here, we develop a model of change detection inspired by the neural architecture of an evolutionarily conserved “midbrain attention network,” which comprises the superior colliculus (SC) and an associated inhibitory nucleus [isthmi pars magnocellularis (Imc); Knudsen, 2011].
Primarily studied for its role in the control of eye movements (Paré and Wurtz, 2001; Port and Wurtz, 2003) the SC plays an important role also in the detection of salient changes in sensory stimuli (Krauzlis et al., 2013; Sridharan et al., 2014; Herman and Krauzlis, 2017). For instance, neurons in the SC, and its extensively characterized nonmammalian vertebrate homolog, the optic tectum (OT), fire robustly in response to changes in luminance and size of stimuli (Knudsen, 2011; Liu et al., 2011; Barker et al., 2021; Heap et al., 2018). Many studies have shown that the SC/OT is involved in the detection of salient change events, in a variety of species, including frogs (Gaillard, 1990), birds (Wu et al., 2005), and rats (Comoli et al., 2003). More recent studies have shown that neurons in the primate SC produce phasic bursts of activity in response to near-threshold changes in stimulus color saturation (Herman and Krauzlis, 2017). Moreover, reversibly inactivating the primate SC produces deficits with detecting changes in motion-direction change detection tasks (Zénon and Krauzlis, 2012), and microstimulating the SC enhances the ability to detect changes (Cavanaugh and Wurtz, 2004; Cavanaugh et al., 2006). The SC/OT along with the inhibitory (GABAergic) nucleus Imc (Fig. 1A) are hypothesized to play a key role in signaling of the highest priority stimulus in dynamic environments (Knudsen, 2018).
Figure 1.
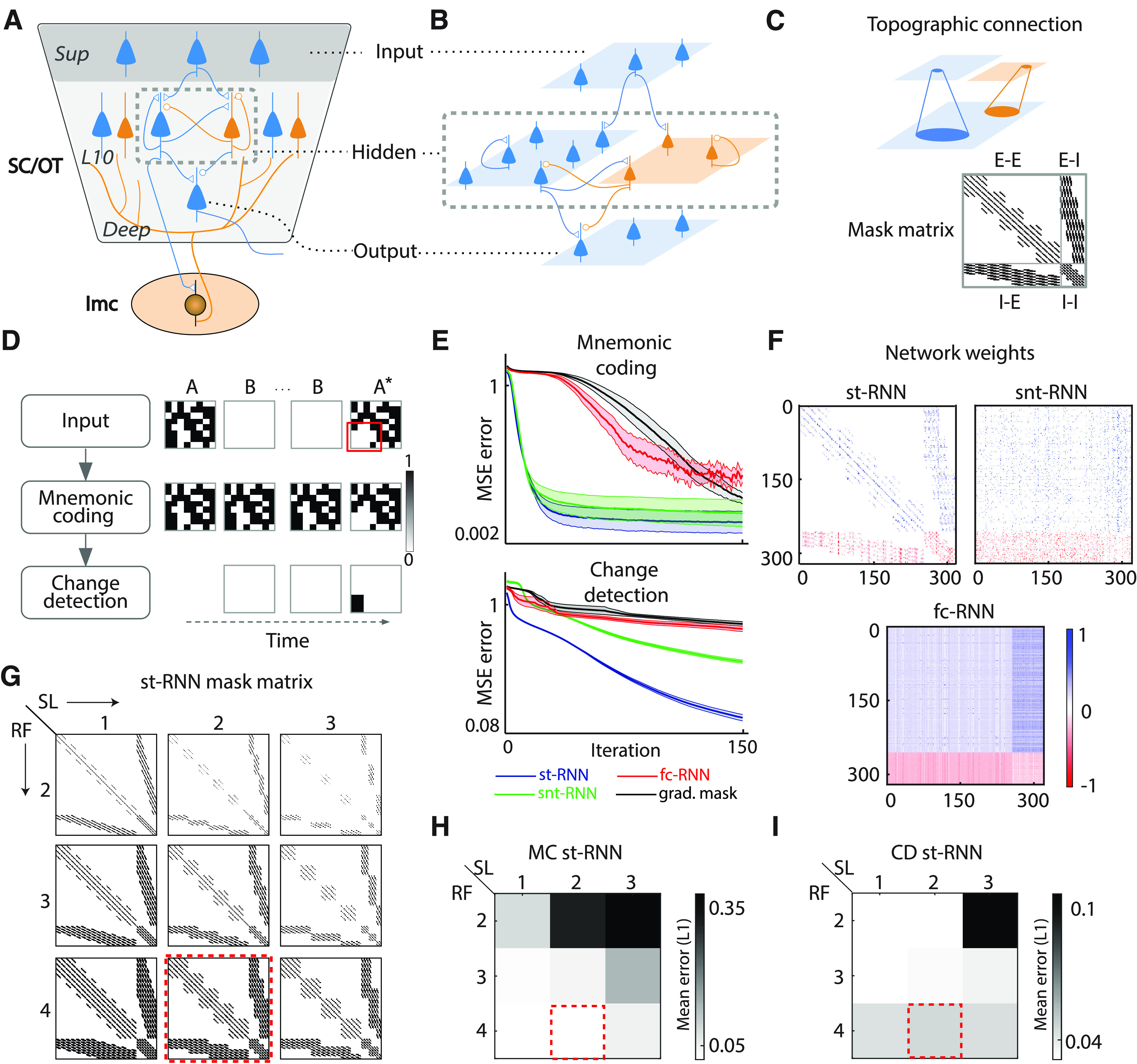
A midbrain-inspired st-RNN model. A, Schematic showing key components of the midbrain attention network (Knudsen, 2018). The SC, or its non-mammalian vertebrate homolog, the OT, is a multilayered structure with recurrently connected excitatory (E; blue) and inhibitory (I; orange) neurons. Superficial layers (Sup) receive visual inputs whereas intermediate and deep layers (L10, Deep) project to other brain regions and to oculomotor centers. Dashed gray rectangle, Neurons in layer 10 that project topographically to a midbrain GABAergic nucleus (Imc; lower ellipse), which provides global inhibition across the SC/OT neural representation (diffuse orange connections). B, Schematic of st-RNN, with connectivity inspired by the midbrain network. Blue: E-neurons, orange: I-neurons, triangles: E-synapses, circles: I-synapses. Input layer (top) and output layer (bottom) comprise 8 × 8 E-neurons with feedforward connections. Dashed gray rectangle: hidden layer comprising 16 × 16 E-neurons and 8 × 8 I-neurons with recurrent connections. C, Top, Schematic of topographic connectivity: each neuron can connect to a spatially restricted neighborhood of neurons only, for both feedforward and recurrent connections. Bottom, Mask matrix (320 × 320) showing permitted (topographic) recurrent connections in the hidden layer. First 256 rows (and columns) correspond to E-neurons and the last 64 rows (and columns) correspond to I-neurons. Each cell (i,j) represents a connection from neuron j to neuron i. E-E and E-I, connections from excitatory to other excitatory or other inhibitory neurons, respectively; I-E and I-I, connections from inhibitory to other excitatory or other inhibitory neurons, respectively. Black: permitted connections, white: disallowed connections. D, Change detection by the st-RNN. Top row, An exemplar binary patch sequence presented as input to the model. A: original image patch; B: blank; A*: changed image patch. Black: “active” pixels; white: “inactive” pixels; red box: location of change (pixels in the lower left). E, Top, Mean squared error (MSE) (log-scale) over the course of training iterations for the mnemonic coding st-RNN (blue), a conventional fc-RNN (red), an RNN with sparse, but not topographic, connectivity (snt-RNN, green), and an fc-RNN with gradients masked with a sparse matrix during learning (black). Shading: SEM across n = 6 different weight initializations and learning rates (Materials and Methods). Bottom, Same as in the top panel, but for the respective change detection RNNs of each network. Other conventions are the same as in the top panel. F, Top left, The final connectivity matrix learned by the mnemonic coding st-RNN. Blue: excitatory synaptic weights (positive values); red: inhibitory synaptic connection weights (negative values); white: no connectivity (synaptic weight of zero). Top right, Same as in the top left panel, but for the snt-RNN. Bottom, Same as in the top left panel, but for the fc-RNN. G, Connectivity masks used for training mnemonic coding (MC) st-RNN and change detection (CD) st-RNN with different sparsity levels (SL) of connectivity and receptive field (RF) sizes of localized, topographic inputs (Materials and Methods). Columns, Left to right, Connectivity patterns with increasing sparsity levels. Rows, Top to bottom, Connectivity patterns with increasing RF sizes. Other conventions are the same as for the mask matrix shown in panel C. H, Performance of the MC st-RNN, quantified with the mean L1 error, during the maintenance epoch, for different sparsity levels (columns) and receptive field sizes (rows) corresponding, respectively, to the connectivity mask matrices shown in panel G. I, Same as in panel H but showing performance of the CD st-RNN. Other conventions are the same as in panel H. G–I, Red dashed squares, Sparsity levels and receptive field sizes used in subsequent model simulations.
We develop a midbrain inspired deep learning model of change detection, specifically, for the challenging scenario of “change blindness”: the surprising inability to detect salient changes in visual scenes when attention is not deployed at the location of change (Rensink et al., 1997; Gibbs et al., 2016). Change blindness is assessed, in laboratory settings, by presenting a pair of alternating images that differ in some important detail, typically, with intervening blank frames (“flicker” paradigm; Rensink et al., 1997). In such tasks, subjects are instructed to scan the images by moving their eyes to different parts of the image to identify the location of change. Both human observers and models must address a key challenge when detecting changes in such change blindness tasks. If the pair of images were presented on consecutive frames, a motion-like signal would occur at the location of change, rendering it relatively easy for human observers to detect the change (Tse, 2004). Similarly, a computational model can accomplish change detection with the relatively trivial operation of computing a difference in input pixel values across successive frames. On the other hand, in change blindness tasks changes occur interspersed by a blank frame, which precludes the appearance of motion signals localized to the change. Consequently, simple operations, like pixel-level differencing of the input, do not suffice to localize the change in change blindness tasks.
To model change detection in this challenging setting, we turn to recurrent neural network (RNN) models. RNNs constitute a versatile class of deep learning models that are routinely deployed for modeling various cognitive behaviors (Sussillo and Barak, 2013; Sussillo, 2014). These include cognitive tasks involving perceptual decision-making, multisensory integration, working memory (Song et al., 2016), delayed estimation, change detection, forced choice comparison (Orhan and Ma, 2019), signal detection and context dependent discrimination (Mastrogiuseppe and Ostojic, 2018), among others. RNNs are also increasingly used for accurate decoding of neural dynamics in brain machine interfaces (Sussillo et al., 2012; Pandarinath et al., 2018), suggesting their potential utility for understanding the link between complex neural dynamics and cognitive states.
Here, we introduce a biologically constrained RNN, which we call a sparse, topographic RNN (st-RNN). The st-RNN is closely modeled on detailed neuroanatomy of the midbrain SC/OT and the Imc (Knudsen, 2018; Fig. 1A). In addition to being trained more rapidly, the st-RNN achieves change detection with far fewer connections than conventional RNN models. Moreover, low-dimensional dynamics of the st-RNN provide essential insights into key neural computations underlying change detection in the midbrain. Lastly, by having the st-RNN model drive an eye movement (saccade) algorithm, we predict human gaze fixations in a laboratory change blindness experiment, surpassing state-of-the-art. In sum, the st-RNN provides a novel deep learning framework that may enable linking neural computations underlying change detection with their associated psychophysical mechanisms (Krauzlis et al., 2013; Sridharan et al., 2014).
Materials and Methods
Ethics declaration
Behavioral data from a change blindness experiment reported previously (Jagatap et al., 2021) were re-analyzed for this study. For that study, informed consent was obtained from all participants; other details are reported elsewhere (Jagatap et al., 2021). Experimental protocols were approved by the Institute of Human Ethics Review board at the Indian Institute of Science (IISc), Bangalore.
st-RNN model
We designed an RNN model, incorporating neurobiological constraints, by modifying the architecture of conventional RNNs. We implemented sparse, topographic connectivity among neurons of every layer, while also incorporating Dale's law, which specifies that each neuron connects with its downstream targets exclusively with either excitatory or inhibitory synapses. Thus, the connection weight matrix between different layers of the network was specified as:
| (1) |
where SM(.) is a sign matrix, whose elements (+1 or −1) determines E versus I connectivity, respectively, among the different neurons, CM(.) is a mask matrix that determines the connections permissible under topographic connectivity constraints (Fig. 1C), × denotes matrix multiplication, denotes element-wise multiplication, and []+ denotes rectification (Song et al., 2016). The topographic connection mask matrix (CM) was specified as follows (Fig. 1C): each hidden layer neuron received input from overlapping tiles of either 4 × 4 (input-hidden layer E and I, hidden layer E-E, I-E, I-I) or 8 × 8 neurons (hidden layer E-I). Similarly, each hidden layer neuron (E and I) projected to tiles of 4 × 4 neurons in the output layer. Neurons proximal to the corners of each layer received input from and projected to only one such tile. Neurons proximal to the edges, either horizontal or vertical, received input from and projected to two overlapping tiles. Neurons in the center of each layer received input from, and projected to, four overlapping tiles. Levels of overlap were different for different connections (one neuron for E-E connections, two neurons for input-E, input-I, I-E, and I-I connections, and four neurons for E-I connections). The mask matrix shown in Figure 1C represents unfolding of the neurons in E and I layers in a column-first manner, with E neurons first, followed by I neurons. Note that this pattern represents constraints on connectivity in the network; the final connection weights were determined following network training (see below, st-RNN training and testing). As the precise ratio of E:I neurons in the SC is not known, we adopted the canonical 4:1 ratio, observed in the neocortex (Xue et al., 2014). Thus, each st-RNN module comprised an input layer (8 × 8 = 64) with only excitatory neurons, a hidden layer comprising separate excitatory (16 × 16 = 256) and inhibitory (8 × 8 = 64) neuron layers, and an output layer (8 × 8 = 64) also comprising only excitatory neurons. Finally, RNN dynamics were simulated with ordinary differential equations, with dynamics discretized in time, as follows:
| (2) |
where xt, rt and ot are the activity of the input, recurrent layer, output neurons at time t, respectively; st represents a latent variable, that can be construed as the net input into the recurrent layer; Ueff, Veff, and Weff are input-hidden, hidden-output and recurrent hidden layer connectivity matrices, bo is output bias, f(.) is the hyperbolic tangent function, and g(.) is a sigmoid nonlinearity. The results presented here were fairly robust to the choice of these nonlinearities; for example, a sigmoid nonlinearity in the hidden layer also produced results similar to those presented here. All simulations were performed with the Tensorflow framework (Abadi et al., 2016).
In addition, we tested the effect of (1) varying the level of sparsity in the connections, and (2) varying the receptive field (RF) size of local, topographic connections, both among the hidden layer units. RF sizes were varied by interconnecting neighboring neurons in blocks of size (RF or r = 2, 3, 4; Fig. 1G). Sparsity levels were controlled, independently of RF sizes, by skipping connections (varying the stride) across adjacent neurons in a block, so that the lowest sparsity level (SL = 1, densest connectivity) contained ∼45% of all possible connections within a block, whereas the intermediate (SL = 2) and highest (SL = 3) sparsity levels contained ∼40% and ∼35% connections, respectively (Fig. 1G).
Architecture incorporating a global inhibitory (GI) layer
In some simulations, we also modeled input to the hidden layer units of each st-RNN module from a GI layer (10 × 8 = 80 neurons; Fig. 4A). The GI layer received strong convergent input from the input layer units, and its output was obtained by topographic spatial convolution of the input layer activity with a box-filter of size 11 × 11, followed by nearest-neighbor downsampling to 10 × 8 resolution, and binarization by rounding. These input weights to the GI layer were not trainable (fixed weights). The resultant 10 × 8 binary-map was treated as the output of GI layer. No recurrent connections occurred in the GI layer. The GI layer projected to the hidden layer neurons (recurrent units) of the st-RNN modules through inhibitory connection weights (Ug; Eq. 3, below). These weights were trainable and were randomly initialized before training. The hidden layer unit activations were, then modeled as:
| (3) |
where is the output of the GI units, and Ug is inhibitory connection matrix from the GI units to the hidden layer units of the st-RNNs. Note that only one st-RNN module was trained along with the GI layer. For modeling images with tiled st-RNNs, GI layer weights were replicated across all, tiled st-RNN modules. Simulations in Figures 4, 7, 8 were performed with this version of the network incorporating the GI layer.
Figure 4.
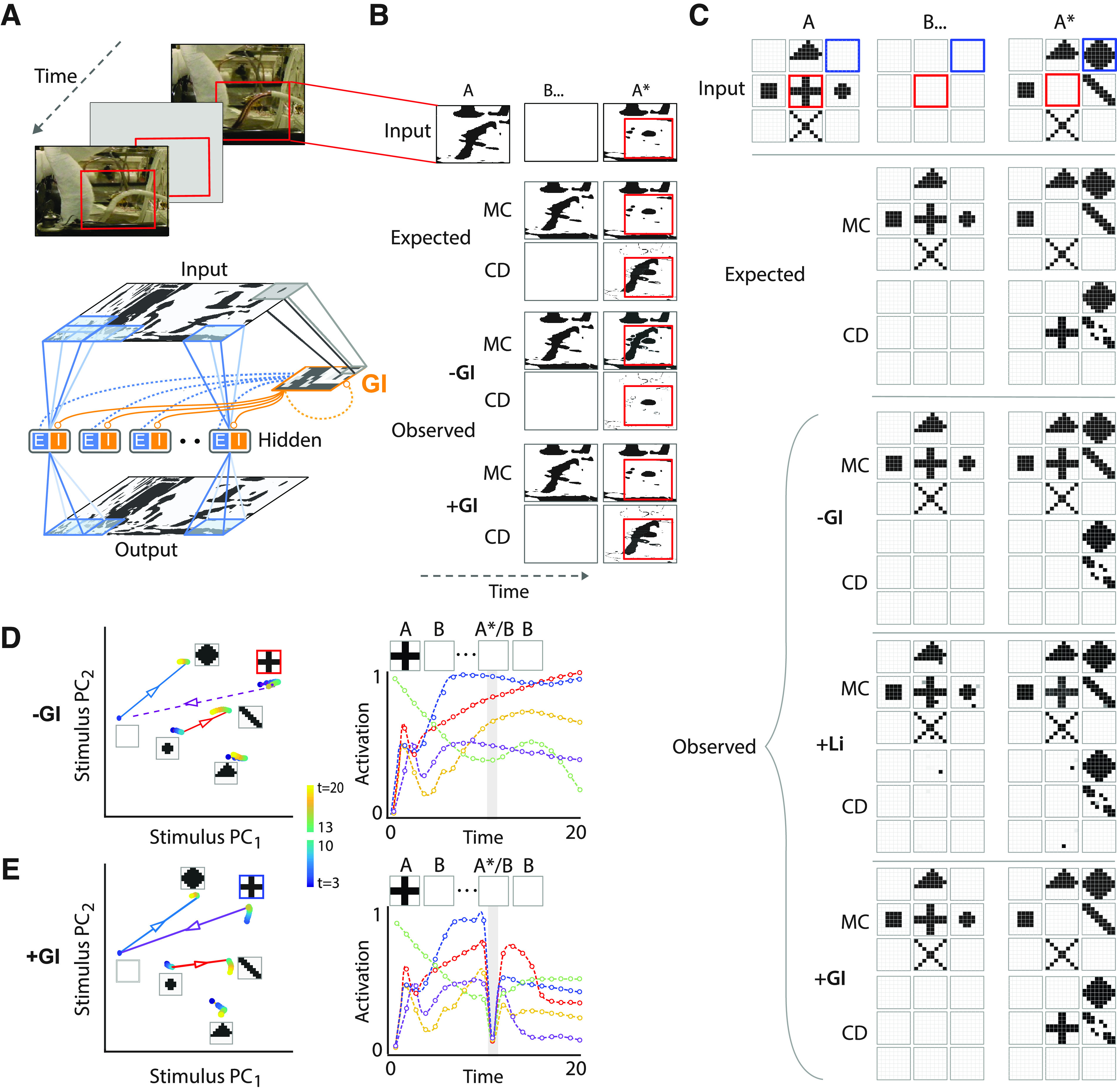
Global inhibition enables change detection with natural images. A, Top, Schematic of change detection with a representative natural image (resolution: 1024 × 768), interspersed by blanks. Red rectangle: location of change (not part of the image). Bottom, 8 × 8 st-RNN modules tiled to represent the full resolution image (overlapping blue patches in both input and output map). st-RNN modules were tiled with 50% overlap along both horizontal and vertical directions, such that each 4 × 4 patch in the image (except for patches closest to the border) was processed by four different st-RNN modules. Orange outline: global inhibition (GI) layer, mimicking the architecture of the Imc connection (Fig. 1A, orange nucleus). Gray lines: convergent, topographic connections from input to the GI layer; orange circles: inhibitory connections from the GI layer to both E and I neurons in the hidden layer of each st-RNN module; dashed connections: recurrent excitatory connections from E neurons in the hidden layer to neurons in the GI layer (in blue) and recurrent inhibitory connections among neurons in the GI layer (in orange); these connections were implemented in one variant of the network incorporating the GI layer (Materials and Methods). B, Topmost row, Thresholded, binarized saliency map around the region of change (red box; see text for details). Second and third rows, The expected output (ground truth) of mnemonic coding (MC) and change detection (CD) st-RNNs, respectively. Fourth and fifth rows, Output of the trained MC and CD st-RNN models before incorporating the global inhibition layer (−GI). Sixth and seventh rows, Output of the trained MC and CD st-RNN models after incorporating the global inhibition layer (+GI). For all rows, the middle and right columns represent the output of the respective st-RNN during the blank (B) and change image (A*) epochs, respectively. Red outlines: location of change. C, Analysis of a toy-example with nine st-RNN modules tiled in a 3 × 3 square grid, with no overlap. Rows 1–3, Input to the st-RNN modules (1st row), and the expected ouputs of the MC st-RNN (2nd row), and CD st-RNN (3rd row). Rows 4–9, Outputs of the trained MC and CD st-RNN models before incorporating the global inhibition layer (–GI; 4th and 5th rows), after incorporating local (short-range) recurrent interactions (+Li; 6th and 7th rows), and after incorporating the global inhibition layer (+GI; 8th and 9th rows). Other conventions are the same as in panel B. Top row, Red box: on-off transition; blue box: off-on transition. D, Left, Projection of hidden layer activity for each st-RNN (panel C) into the mnemonic subspace, in the absence of global inhibition (−GI). Trajectories begin from the first blank, when the first image was maintained (blue shaded dots; t = 3–10), through a transition corresponding to the presentation of the change image (lines with superimposed arrowheads), followed by the second blank, when the change image was maintained (green to yellow shaded dots; t = 13–20). Insets, Input images for each st-RNN module from the toy example (panel C). The st-RNN failed to accomplish the on-off transition (“plus” shape to blank) successfully (dashed purple arrow). Right, Activity of five representative hidden layer units, each represented by a different color, of the mnemonic coding st-RNN corresponding to the middle pattern (“plus”) from panel C. In absence of global inhibition (–GI) unit activity failed to reset on presentation of the change image (A*). Dots: data for each bin; dashed lines: spline fits; gray shaded bar: time point (t = 11) corresponding to presentation of the change image. E, Same as in panel D but in the presence of global inhibition (+GI). Left, The st-RNN accomplished the on-off transition (“plus” shape to blank) successfully (solid purple arrow). Right, In the presence of global inhibition (+GI) unit activity “reset” on presentation of the change image (gray shading).
Figure 7.
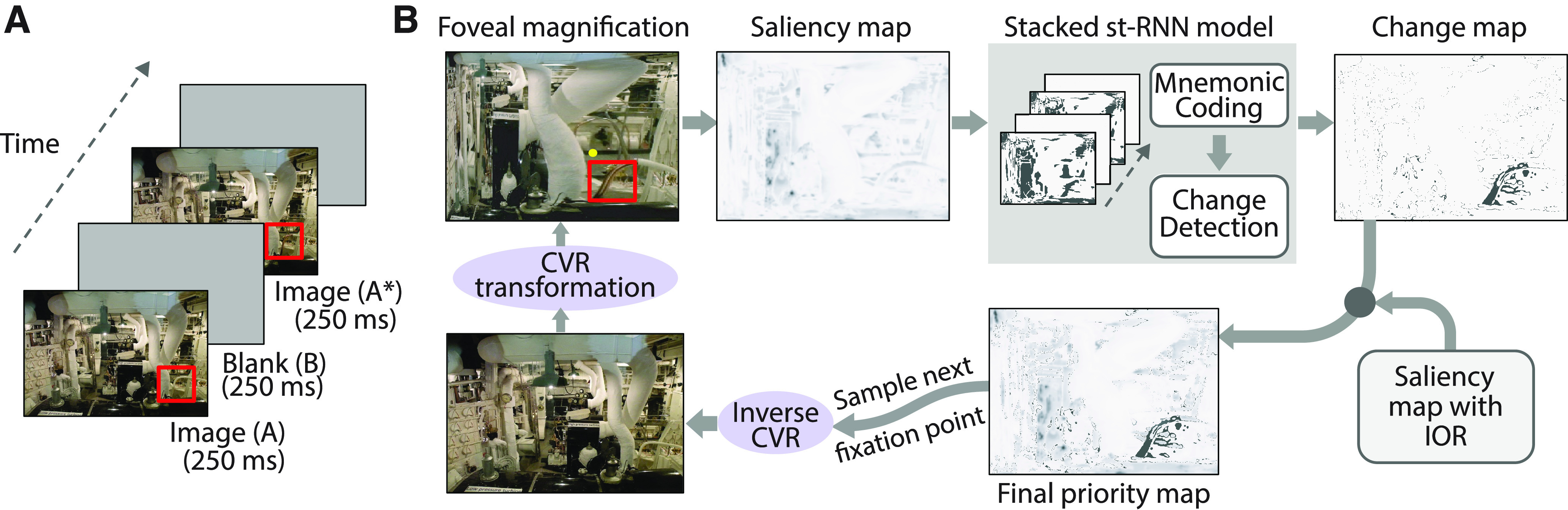
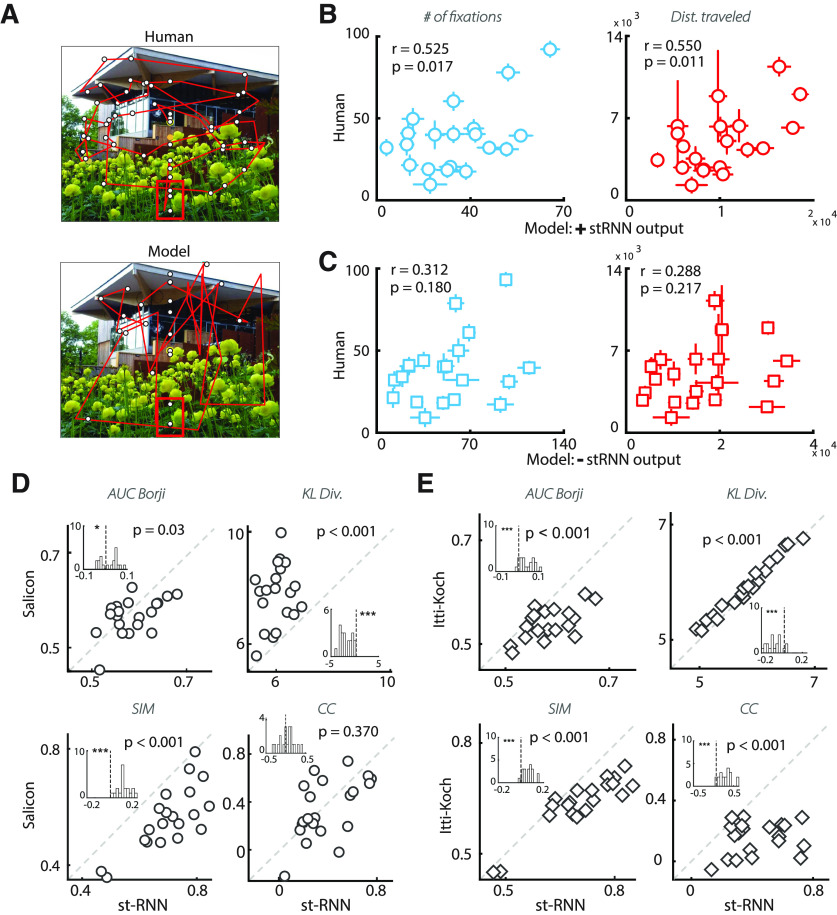
A gaze model for simulating eye movements with the st-RNN model. A, A representative sequence of stimuli in the change blindness experiment. Images, with a key change between them (red box indicates location of change), were alternated for 250 ms each, with intervening blank frames, also presented for 250 ms (“flicker” paradigm). In the laboratory experiment, participants were required to scan the image and detect the change within a fixed trial duration (60 s). B, Steps involved in simulating sequential fixations with the st-RNN model. Clockwise from top left, Following fixation (yellow dot), the image was foveally magnified with a CVR transform. Following this a bottom-up saliency map was computed (Itti et al., 1998), thresholded and binarized (for details, see Materials and Methods). The temporal sequence of binarized saliency maps was provided to the stacked st-RNN model to obtain the Change map (output of the change detection st-RNN; top right). The Saliency and Change maps were then fused along with an IOR map to obtain the final Priority map (bottom; Materials and Methods). This final map was converted into a probability density and used to sample the next fixation point.
Figure 8.
st-RNN based gaze model mimics and predicts human strategies in a change blindness task. A, Comparison of gaze scan path for a representative human subject (top) versus a model's trial (bottom) on an example image from the change blindness experiment. Red box: location of change. B, Correlation between model (x-axis; average across n = 80 iterations) and human data (y-axis; average across n = 39 participants) for the number of fixations (left) and distance traveled (right) before fixating on the change region. Error bars: SEM. C, Same as in panel B, but for a model in which the priority map was computed after excluding the st-RNN output (see Materials and Methods). D, Distribution of four different saliency comparison metrics across 27 images for the fixation map predicted by the st-RNN model (x-axis) versus the map predicted by the Salicon algorithm (y-axis) (Huang et al., 2015). Clockwise from top: AUC (Borji), KL-divergence, CC and similarity. Diagonal line: line of equality (x = y). For all metrics, except for KL-divergence, a higher value implies better match with human fixations. Insets, Distribution of difference between the st-RNN and Salicon prediction for each metric. E, Same as in panel D but comparing fixation predictions of the st-RNN model (x-axis) against that of the Itti–Koch saliency prediction algorithm (y-axis). Other conventions are the same as in panel D.
We also trained a variant of the network in which the GI layer neurons received topographic excitatory input from the st-RNN hidden layer excitatory (E) neurons; these weights (matrix ; Eq. 4) were trainable. The GI layer comprised of 100 neurons, organized in a 10 × 10 grid and also contained all-to-all recurrent inhibitory connections (matrix ; Eq. 4). As before, GI units inhibited the st-RNN hidden layer units using weight matrix (Eq. 3). The GI layer unit activations were modeled as:
| (4) |
where represents the convergent input from the input layer (10 × 10), is a trainable weight matrix that transforms the input to GI layer dimensions. For modeling high-resolution images with tiled st-RNNs, GI layer unit weights were shared across all tiled st-RNN modules, with representing averaged hidden excitatory unit activations across all the tiled st-RNN modules. Simulations in Figures 5 and 6 were performed with this version of the network.
Figure 5.
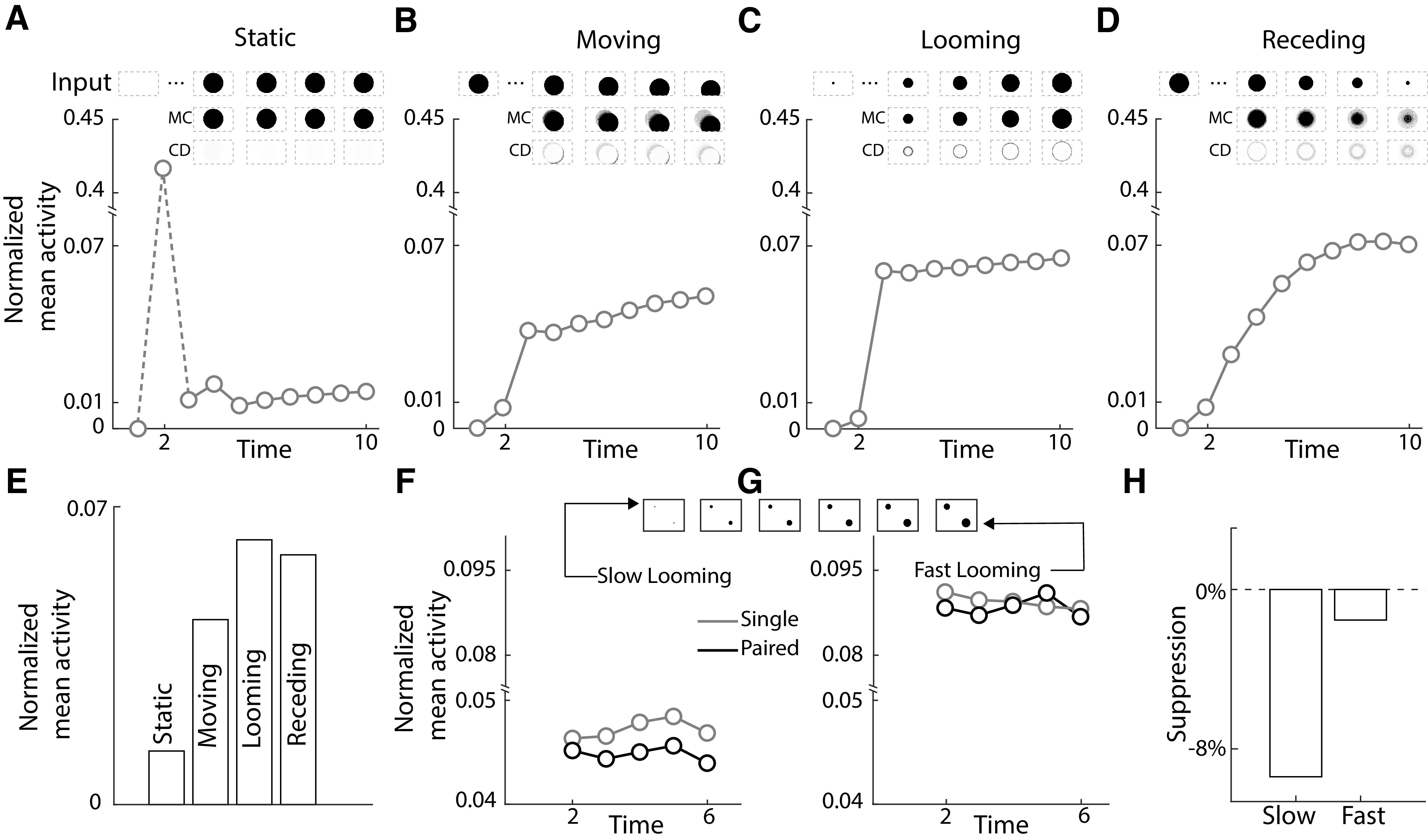
Model unit responses to static, dynamic and competing stimuli. A–D, Normalized mean activity of output units (n = 62,500) of the change detection st-RNN for static (A), moving (B), looming (C), and receding (D) stimuli. Mean activity was normalized by the maximum activation across all four stimulus classes. Insets, Input stimulus patterns for each, respective, simulation. Insets, First row, Input sequence corresponding to each stimulus type (A–D). Insets, Second and third rows, Mnemonic coding (second row) and change detection (third row) outputs corresponding to the respective stimulus type. E, Normalized mean activity of the change detection st-RNN output units averaged across the final seven frames (t = 3 to t = 10) for static (S), moving (M), looming (L), and receding (R) stimuli (see text for details). F, Same as in panels A–D except showing activity evoked by a slow-looming stimulus in the upper left quadrant when presented alone (“Single,” gray) or concurrently with a fast-looming stimulus (“Paired,” black). Inset, Paired input stimulus pattern. Other conventions are the same as in panels A–D. G, Same as in panel F, but showing activity evoked by the fast-looming stimulus. Other conventions are the same as in panel F. H, Suppression of the mean activity (percentage) for paired, as compared with single, across the last five frames (t = 2 to t = 6), for neurons representing the slow-looming (left bar) and fast-looming (right bar) stimuli, respectively.
Figure 6.
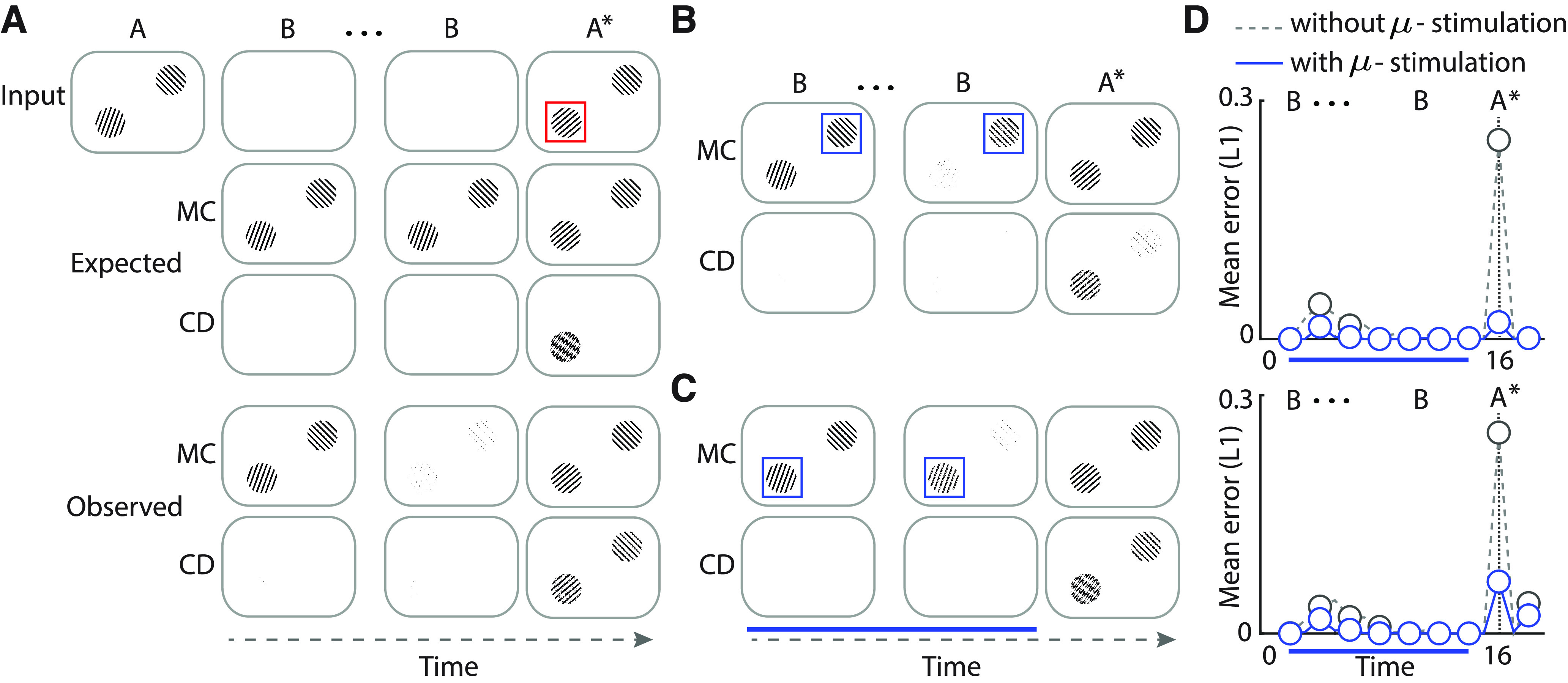
Simulated microstimulation rescues change detection deficits. A, Top row, Simulated laboratory change blindness task. Two oriented gratings were presented, one in each visual hemifield. The entire image spanned 1000 × 800 pixels and was encoded with 50,000 overlapping st-RNN modules. Following the blank (B), a new change image occurred in which one of the gratings (here, the grating in the left hemifield) underwent a change in orientation. Middle row, Output of the mnemonic coding (MC) st-RNN. Bottom row, Output of the change detection (CD) st-RNN. Red box: location of change, is shown for illustration only, and is not presented along with the visual input. Other conventions are the same as in Figure 4B. B, The output of the mnemonic coding (first row) and change detection (second row) st-RNNs following simulated, focal microstimulation of the right hemifield (no-change) grating representation alone (see text for details). C, Same as in panel B but following simulated, focal microstimulation of the left hemifield (change) grating representation alone. Other conventions are as in panel B. B, C, Blue box, Location of simulated microstimulation, is shown for illustration only and is not presented along with the visual input. Blue horizontal bar: duration of microstimulation. D, Quantification of change in performance following the simulated microstimulation experiments of panel B (top) and panel C (bottom), respectively. Top, Mean L1 error for units representing the right hemifield (no-change) grating without (gray dashed) or with (blue solid) simulated microstimulation. Dashed vertical lines: time of appearance of the changed image (A*). Other conventions are the same as in panel C. Bottom, Same as in the top but mean L1 error for units representing the left hemifield (change) grating. Other conventions are the same as in the top panel.
st-RNN training and testing
Two st-RNN modules operated, in sequence, to solve the change blindness task (Fig. 1D; see Results). Each st-RNN was trained by learning the following parameters: W, U, Ug, V, bo. Because mnemonic coding (maintenance) and change detection are independent, separable, operations, each st-RNN could be trained independently of the other, and with separate training datasets comprising 200,000 synthetic 8 × 8 binary patches. Each binary patch (A) was generated to provide input patterns of prespecified sparsity (proportion of active pixels) drawn from a uniform random distribution, ranging from 0.1 to 1. For each binary patch A, an alternate (change) patch A* was generated by setting pixels active or inactive randomly with 50% probability, independently for each pixel. During training, the input to each st-RNN comprised a sequence of 10 images, beginning with a binary patch (A), succeeded by a variable number of blanks (median = 2, range = 1–8), followed, finally, by the changed binary image (A*). The distribution of variable blanks was determined during training, by deciding with 50% probability, at each time step, whether a blank or the changed image would be shown. We employed a variable number of blanks to ensure that the RNN learned a general strategy of change detection, which did not depend on the precise temporal interval between the original and changed image. The order of presentation of A and A* were counterbalanced to ensure that the number of “onset” versus “offset” type changes (Fig. 1D) were matched in the training dataset. Each st-RNN was trained, in a supervised manner, to minimize the average mean squared error (MSE) between st-RNN output and expected (ground-truth) activation in the output layer (optimizing the L2-loss function) across time steps. Both st-RNNs were trained until the change in the loss function plateaued (Fig. 1E), and subsequently tested on a validation corpus of 20,000 new image patches each.
st-RNN weights were initialized to ensure that they obeyed the constraints on topography and Dale's law. For this, we adopted truncated Gaussian initialization to initialize connectivity matrices with random positive or negative values; the truncated distribution was chosen to have a mean and standard deviation of 0.2 and 0.01, respectively. During learning weights were masked with the sign mask matrix, SM, to segregate E and I connection types, as described above. Unlike Song et al. (2016), we did not adopt explicit regularization to encourage learning of sparse connections. On the other hand, the topographic constraint, defined by the matrix CM above, enforces sparsity by permitting only spatially local connections to be learned (i.e., to assume a non-zero value). Bias parameters of the output connections were initialized with a constant value of zero, throughout.
Training was performed with minibatches of size 128 using adaptive moment estimation based stochastic gradient descent (i.e., Adam optimizer) with a learning rate (L) of 10−4, and exponential decay rates (Kingma and Ba, 2014; is assigned a small value to prevent division by zero). Training was performed by treating the st-RNN as a deep feedforward architecture with identical layers, and shared parameters, unrolled at each timestep (Pascanu et al., 2013). We also performed backpropagation through time over mini-batches of sequence length 10, which enabled the network to learn long-term relationships between the input stimulus and the expected output. Such an approach is particularly essential for the mnemonic coding st-RNN, which needs to maintain its persistent representation in the absence of input, and over the variable durations of the blank epochs (one to eight blanks).
For simulating the fully connected RNN (fc-RNN) network (Figs. 1E,F), the connectivity equations were the same as above except that we removed the constraint on sparse topographic connectivity (matrix CM; Eq. 1). Other aspects of training and testing were identical to that of the st-RNN network, described above. Both st-RNN and fc-RNN were trained with different learning rates (L = 0.0001, 0.005, 0.001, 0.05, 0.01) and five random weight initializations; the shading in Figure 1E reflects the standard error across these different learning rates and initializations.
We also trained and tested the st-RNN modules with inhibitory input from a global, inhibitory layer (GI layer; Fig. 4A). Training exemplars were chosen similarly as described above for training the model without the GI layer, except that in this case we also included completely blank images as potential change (A*) images. To mimic change in global context (e.g., the appearance of a new image), two 8 × 10 patterns, each with randomly activated pixels (binary maps with sparsities ranging from 0.4 to 0.6) provided GI input to all hidden layer units at two distinct time-steps, at the time of appearance of A and A*, respectively, with blanks in between. While we could have chosen to provide input directly from the input image to the GI layer, random inputs sufficed to illustrate the following idea: for flexible updating, GI layer neurons needed to be activated during the presentation of new images but could remain agnostic to the precise content of those images. All other training and testing steps were the same as described above for the st-RNN module. Again, as before, the st-RNN network with global inhibition was trained with 200,000 training sequences and validated with 20,000 new sequences. When tested with the full, high-resolution image, the 8 × 10 patterns that provided global context, were drawn from the output of the GI layer (Fig. 4A). A similar procedure was used for training the st-RNN modules with recurrent connections to the GI layer (Fig. 4A, dashed connections).
Estimating the total number of connection weights and parameters
Based on the above architecture, we estimated the total number of weights in an st-RNN module (8 × 8 input/output, hidden layer with 16 × 16 E neurons and 8 × 8 I neurons, and a 10 × 8 GI layer) to be 46 080; these included feedforward connections from neurons in every layer to each successive layer (input, hidden, output), feedforward connections from the GI layer, as well as recurrent connections between neurons in the hidden layer. For designing an st-RNN to encode a 1024 × 768 high-resolution image with each neuron in the input layer encoding one image pixel, the number of units in each layer would have to be scaled up by ∼104 times the current configuration. This would yield a scaling up of the total number of weights in the network to ∼3.8 × 1012, a prohibitively large number that is impractical for training. As a result, we trained a single 8 × 8 module and tiled this module (with shared weights) across both x- and y-directions to cover the span of the 1024 × 768 high-resolution image (see Materials and Methods, Modeling change detection with high-resolution images).
Computing the mnemonic subspace
We examined the representation of the st-RNN hidden layer unit dynamics in a mnemonic subspace (Druckmann and Chklovskii, 2012; Murray et al., 2017). Each unique input pattern is expected to have a corresponding unique latent representation in this mnemonic subspace and trajectories of the latent representation of each input pattern should be stable (and not drift) in the absence of input (Druckmann and Chklovskii, 2012; Murray et al., 2017).
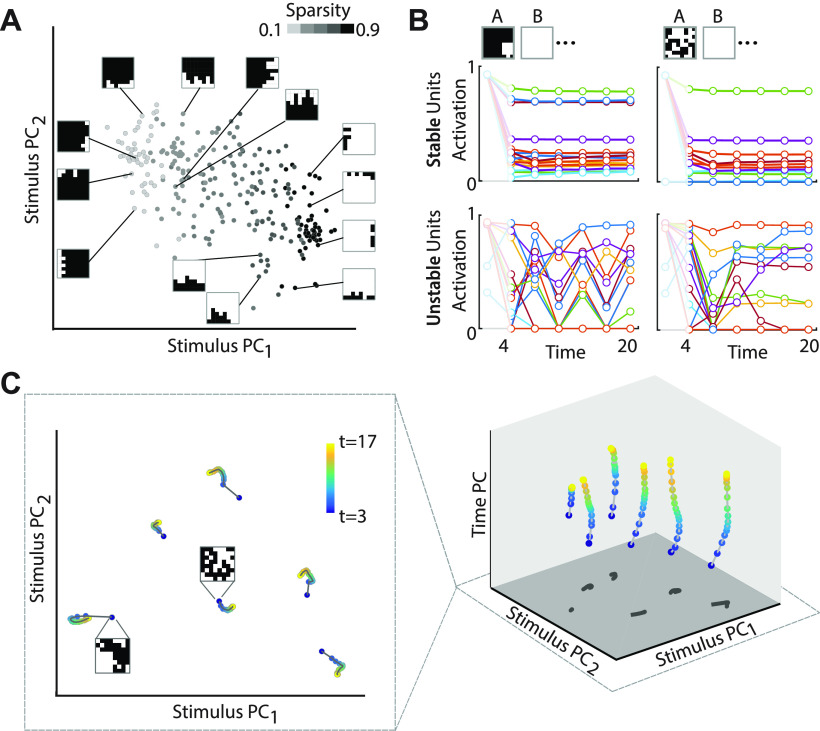
To obtain this mnemonic subspace, we performed principal components analysis (PCA) on the time-averaged activity of the of hidden layer units of the mnemonic coding st-RNN, during the blank period; for this analysis, activity in the first two time bins was excluded, to permit activity in the “stable” neurons to stabilize (Fig. 2B). Thus, PCA was performed on an mxn matrix, where m is the number of unique input patterns and n = 320, including 256 excitatory and 64 inhibitory hidden layer neurons. The first two principal component (PC) vectors were designated as “Stimulus PC1” and “Stimulus PC2”; these vectors span the two-dimensional mnemonic coding subspace (Fig. 2A). The activity of the hidden layer neurons at each time-step was then projected onto this subspace to obtain a two-dimensional trajectory during the maintenance epoch, following each input patch presentation (Fig. 2C, left). Next, a “Time PC” was obtained by computing first principal direction after subtracting the time-averaged activity across each stimulus. Thus, PCA was performed on a (m.t)xn matrix, where t = 17 is the number of time bins during the delay period (excluding the first three time bins). The Time PC was then orthogonalized relative to the Stimulus PCs by finding the closest orthogonal projection to the two-dimensional mnemonic subspace. Finally, the hidden layer neuron activity was projected into this Stimulus+Time PC representation to obtain three-dimensional trajectories of the hidden layer units during the maintenance epoch. 95% of the variance in the temporal dynamics could be explained by as few as 40 time PCs; similarly, 95% of the variance in the stimulus patterns could be explained by as few as 34 stimulus PCs. Given that the full dimensionality of the hidden layer was 320 (256 excitatory and 64 inhibitory neurons), nearly all of the variance (dynamics or patterns) could be accounted for, therefore, with subspaces that were nearly 8- to 10-fold smaller in dimensionality. Unit activities during specific epochs were then projected onto this mnemonic subspace (Figs. 2A,C, 4E,D).
Figure 2.
Stable maintenance occurs in a “mnemonic” subspace despite heterogenous dynamics of individual units. A, Projection of input stimulus patterns in the mnemonic subspace. “Stimulus PC1” and “Stimulus PC2” correspond to the two PC dimensions with the largest variance across time-averaged representations of the mnemonic coding st-RNN hidden layer units. Points with lighter shades of gray represent input patterns of lower sparsity (proportion of active pixels). Insets, Specific 8 × 8 input patterns. B, Top row, Activity dynamics of the top 16 hidden layer units with the most “stable” dynamics (see text for details) in the mnemonic coding st-RNN during the blank epoch (t = 4–20); each color denotes dynamics for a different unit. Dots: data for every third time bin; lines: data for each time bin. Bottom row, Same as in top row but for the top 16 hidden layer units with the most “unstable” dynamics. Left and right columns, Results for two exemplar input patterns. Several units show overlapping activity profiles. C, Left, Low-dimensional trajectories obtained by projecting the hidden layer unit activity onto the mnemonic subspace during the maintenance epoch. Each cluster of points corresponds to a different input 8 × 8 pattern (insets). Blue to yellow: time points ranging from early (t = 3) to late (t = 17) in the blank epoch. Right, Same as in the left panel, but trajectories plotted with an additional dimension along the z-axis indicating a “Time PC” corresponding to a PC dimension with maximal variance in input-averaged activity across time that is also orthogonal to the mnemonic subspace. Dark-gray trajectories on the xy-plane indicate the projection of the trajectories in the mnemonic subspace.
Stable network output despite unstable activity in individual units
We seek to show analytically how stable activity can emerge in our st-RNN network despite unstable dynamics in individual neurons (Fig. 2B,C). We derive below a sufficient condition for stability of the output representation in our model and verify that this condition holds in our simulated network, modifying a previous framework (Druckmann and Chklovskii, 2012). For convenience, we rewrite the equations for the st-RNN module dynamics (Eq. 2) as:
| (5) |
where is a nonlinearity that encapsulates both and the rectification . To ensure that the output of the st-RNN network is stable, must be unchanging with time . In Equation 5 above, biases are constants. Therefore, for stable output, must be unchanging with time. Because ours is a discrete time model, we represent this condition as . We rewrite this condition, based on st-RNN module dynamics equations as:
| (6) |
where we have dropped the superscripts “eff” from the connectivity matrices, for simplicity. During the maintenance epoch . Setting this value, and expanding the matrix multiplications above in terms of their component terms:
| (7) |
where represents the vector of output connection weights from neuron in the hidden layer to all neurons in the output layer and represents the recurrent connection weight from neuron to neuron , both in the hidden layer. To simplify the analysis, we linearize the equation (by removing the nonlinearity ) and write Equation 7 as:
| (8) |
where in the last step, we have exchanged dummy subscripts and in the first term on the left-hand side. Simplifying further:
| (9) |
For this condition to be true for all pattern dynamics , it is sufficient that the term inside the parenthesis in the left-hand side of the Equation 9 is zero, i.e., it can be stated as:
| (10) |
Equation 10 is, therefore, a sufficient condition for stable activity to emerge in the network output in the absence of external input. We test whether this condition was met in our trained st-RNN network. Because of the simplification associated with linearization of the term (Eq. 8), and because the tanh is a saturating nonlinearity, we normalized the vector on either side before comparing their similarities:
| (11) |
where the asterisk denotes unit normalization of the magnitude of the respective vector. In the trained mnemonic coding network, we quantified the similarity between the unit normalized st-RNN output vectors (320 vectors of size ) on the right-hand side and left-hand side of Equation 11 with their, respective, dot products. A dot product of indicates overlap, and lower magnitudes of dot products indicate progressively less overlap. In the case of our st-RNN mnemonic coding network, we discovered that the dot-product magnitude was (median [ confidence intervals]; across n = 108 output vectors with non-zero magnitudes). These results indicate the stability condition (Eq. 11) was reasonably well met in our data, validating our analysis of output stability in the st-RNN network.
Experiments with silencing specific connections, stable or unstable units
We evaluated change detection performance after silencing specific types of recurrent, hidden-layer connections (E-E, E-I, I-E, or I-I), while holding all of the other types of connections intact (Fig. 3D–G). This was achieved by simply setting the respective weights in the Weff matrix to zero. In addition, we examined the relevance of units with different kinds of dynamics, stable and unstable, for robust change detection. For this, we computed the variance of neural activity during the maintenance period (blank epoch) averaged over 500 random input stimulus patterns. Each hidden neuron was then classified along an axis of most “stable” to most “unstable” by sorting them according to its respective averaged variances. We grouped the top and bottom 5th percentile of these neurons into a “stable” (n = 16) and “unstable” (n = 16) set, respectively. Finally, to evaluate the relative importance of these “stable” versus “unstable” neurons for pattern maintenance, we turned off the output activity of the “stable” and “unstable” subsets, separately, and tested the effect on maintenance. As a measure of the fidelity of maintenance, we computed the mean absolute deviation between the expected output (ground truth) and model output at each time-step (Fig. 3C). This analysis was done using st-RNN module including the GI layer.
Figure 3.
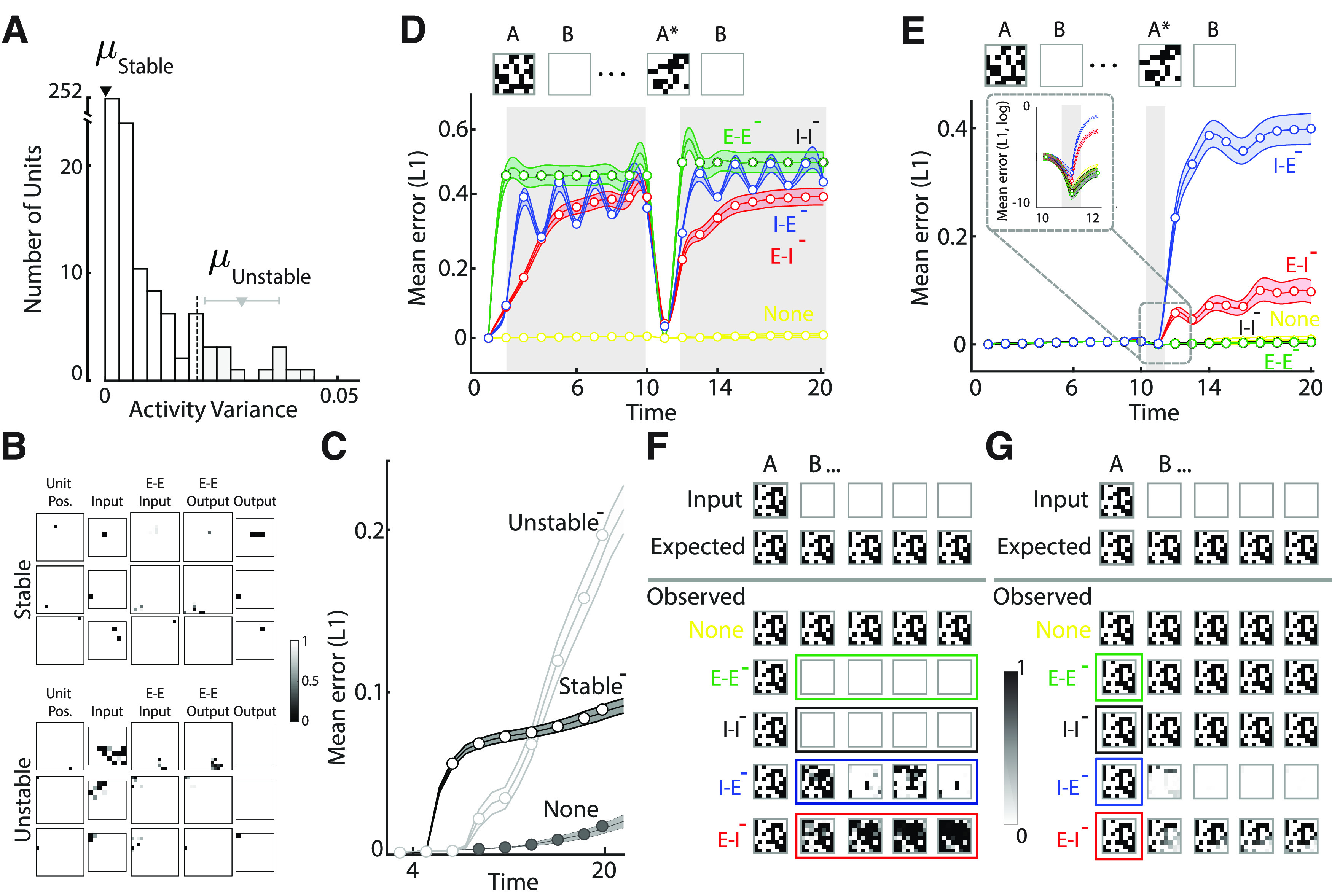
Distinct contributions of unit and connection subtypes to change detection. A, Distribution of variance of activity during the maintenance epoch for all hidden layer units of the mnemonic coding st-RNN. Black and gray inverted triangles: mean activity variance of the units exhibiting the most stable and the most unstable dynamics respectively; dashed vertical line: unstable units with top 5th percentile of activity variance. B, Connectivity kernels of representative stable (top panel) and unstable (bottom panel) excitatory units in the mnemonic coding st-RNN. First column, The unit's location in a 16 × 16 grid. Second column, Feedforward connections from the 8 × 8 input layer to the corresponding unit in the respective row. Third column, Recurrent input from other excitatory hidden layer units. Fourth column, Recurrent output to other excitatory hidden layer units. Last column, Feedforward connections to the output layer units. C, Mean absolute error (L1 norm) between the expected and observed output of mnemonic-coding st-RNN during maintenance (t = 4–20) after silencing the top 5% of stable (“Stable−”; black open circles and curve) and top 5% of unstable (“Unstable−”; gray open circles and curve) units. Dashed line and filled circles: mean absolute error with all units intact (“None”); shading: SEM (n = 500 input patterns). D, Mean absolute error (L1 norm) between the expected and observed output of the mnemonic coding st-RNN following selective silencing of each type of recurrent connection: E-E (green), I-I (black), I-E (blue), and E-I (red). Connections were silenced during the maintenance epochs alone (gray shading, t = 2–10 and t = 12–20). Yellow: mean absolute error but with all connections intact (None); dots: data for specific time points; lines: spline fits; shading: SEM (n = 500 input patterns). E, Same as in panel D but following silencing of recurrent connections only during the presentation of the new image, A* (t = 11; gray shading). Inset, Logarithmic scale plot magnified to show mean absolute error at the time of the change. Other conventions are as in panel D. F, Output of the mnemonic-coding st-RNN for a representative input pattern (topmost row) following silencing of each type of recurrent connection: E-E (green outline, fourth row), I-I (black outline, fifth row), I-E (blue outline, sixth row), and E-I (red outline, seventh row). Second and third rows from top, Expected output and observed output with all connections intact (“None”), respectively. The colored outline indicates the time points during which connections were silenced. Other conventions are the same as in Figure 1D. G, Same as in panel F but following silencing of recurrent connections only during the presentation of the new image. Other conventions are as in panel F.
“Unstable” units are important for stable maintenance
We observed that silencing the activity of unstable units also disrupted stable maintenance (Fig. 3C), in a manner that was comparable to silencing stable units. These results could be readily explained by examining the null space of the output weight matrix (; Eq. 5). For simplicity, we are writing as . In order for the activity of the unstable neurons to not affect the network output, their dynamics should be confined to the null space of In other words, if then the network output would remain unchanged despite silencing the unstable neurons.
Contrary to this hypothesis, we observed that, on average, the activity of unstable neurons was not confined to the null space of (= −0.11, averaged across output units and patterns tested) and was, in fact, comparable to the projection of the stable unit activity onto (; where and denote the activity of the hidden layer “unstable” and “stable” units, respectively). The marginally negative projection of the unstable unit activity onto was possibly a consequence of the larger proportion of inhibitory neurons in the unstable unit subset (11/16), as compared with the stable subset (0/16; see Results).
Tiled st-RNNs with local interactions
We tested whether local interactions among st-RNN modules sufficed to achieve robust change detection (Fig. 4C, +Li, sixth and seventh rows). For this we modeled a network by tiling nine st-RNN modules in a 3 × 3 array, and modeled local interactions between every pair of adjacent modules. The equations for an st-RNN module in each of 3 × 3 modules, describing these interactions are as follows:
| (12) |
where is the output from adjacent st-RNN modules at time and is a local connectivity matrix which specifies the connection weights between the output neurons of one st-RNN module to 10% of randomly selected hidden neurons of the adjacent module. These st-RNN modules were trained and tested in a manner identical to that described previously.
Modeling change detection with high-resolution images
For change detection with natural, high-resolution images (1024 × 768), we tiled 49 152 (256 × 192) st-RNN module pairs, each comprising a mnemonic-coding and change-detection st-RNN, to cover the entire extent of the image. Tiling was performed with 50% overlap along both horizontal and vertical directions (Fig. 4A), such that every 4 × 4 pixel patch (barring those closest to the border) was processed by four different st-RNN modules. The high-resolution image underwent three key transformations before being presented as input to the st-RNN network: (1) foveal magnification with the CVR transform (Wiebe and Basu, 1997); (2) saliency computation with the Itti–Koch saliency algorithm (Itti et al., 1998); and (3) thresholding and binarization based on Otsu's algorithm (Otsu, 1979). These operations are elaborated, next.
First, we modeled a key feature of retinal representation: foveal magnification. When a fixation occurs at a particular region of the image, the representation of the fixated region is mapped onto the fovea with considerably greater spatial resolution, as compared with the periphery. We modeled foveal magnification using the Cartesian variable resolution (CVR) transform (Wiebe and Basu, 1997). For a given fixation location (x0, y0) in the original image, the foveally magnified image was obtained with a nonlinear transformation of original image pixel locations (x, y). Let dx = x – x0 and dy = y – y0 be the distance of an arbitrary pixel at location (x, y) from (x0, y0). Then the logarithmic nonlinear transformation is defined as x' = x0 + dvx and y' = y0 + dvy, where dvx = Sfx * ln(β dx + 1) and dvy = Sfy * ln(β dy + 1). Here, the values of the parameters β, Sfx, and Sfy control the extent of central magnification, and the scaling of the transformed image along the azimuth and elevation directions, respectively. β was set to 0.02, whereas Sfx and Sfy were set so as to maintain the foveally magnified image the same overall size as the original image. An illustration of this foveated transformation is shown in Figure 7B.
Second, we modeled a key aspect of image representation in the SC: visual saliency. Recent studies have shown that SC neurons respond to visual saliency (Veale et al., 2017; White et al., 2017); in fact, saliency information appears to reach the SC even before it is available to the visual cortex (White and Munoz, 2017). Thus, input to the network, at each frame, was based on the saliency map for that frame computed with the Itti–Koch algorithm. The Itti–Koch algorithm (Itti et al., 1998) is inspired by neurobiological properties of the visual cortex. Briefly, the map is computed by combining gradients of color, orientation and intensity information at multiple different spatial scales to compute a single, topographical salience map. The algorithm has been widely employed in various studies that seek to model fixation patterns associated with free-viewing of natural sciences (Adeli et al., 2017).
Third, we binarized the saliency map with an adaptive thresholding algorithm (Otsu, 1979). The algorithm tests different threshold values by dividing the image into a background region and a foreground region based on pixel intensities above and below . Defining and as the variance of background and foreground region, the algorithm iteratively searches to find a ζ that minimizes , where and are the number of pixels in the background and foreground respectively. This binarized saliency map, following thresholding, was provided as input to the st-RNN network to detect changes. In neural terms, such a binarizing operation corresponds to filtering the RNN output with a step-like nonlinearity; a property observed in many output neurons in the SC/OT that signal, categorically, the most salient stimuli in the visual environment based on winner-take-all computations (Knudsen, 2018). The foveally magnified, binarized saliency map of high-resolution, natural images was provided as input to the st-RNN for simulations in Figures 4B and 7B.
Modeling visually-evoked responses and stimulus competition
We computed the visually evoked responses of st-RNN model neurons by simulating the presentation of four different kinds of visual stimuli: static, moving, looming and receding. For all of these simulations we tiled 50,000 st-RNN modules with 50% overlap along both x- and y-directions to encode the entire image (1000 × 800).
A static stimulus was simulated as a circle of radius 125 pixels placed at the center of the 1000 × 800 input image across nine frames (t = 2 to t = 10, in this, and all subsequent cases; Fig. 5A, inset). A moving stimulus was simulated by presenting the same input patch as the static case but by moving it by 10 pixels diagonally on each frame, from the center toward the lower right corner of the image (Fig. 5B, inset). A looming stimulus was simulated as an expanding circle of active pixels from a radius of 8 pixels to a radius of 125 pixels (rate of radius increase: 8 pixels per frame) linearly (Fig. 5C, inset). A receding stimulus was simulated as a contracting circle, with an identical set of frames as the looming stimulus, but reversed in sequential order (Fig. 5D, inset). To avoid an onset transient for the moving and receding stimulus cases, the input for first frame (t = 1) was taken to be identical to that of the second frame (t = 2); for the other two cases (static, looming), the first frame was a blank image. The mean activity of a 250 × 250 central patch of output neurons of the change detection st-RNN is plotted in Figure 5A–D. Figure 5E shows the mean steady-state activity, across the final nine frames (t = 3 to t = 10).
To study the effect of stimulus competition in the network we simulated paired looming stimuli (Fig. 5F,G, “paired”): a fast looming and a slow looming stimulus in the lower right and upper left visual quadrants, respectively. The fast and slow looming stimuli were simulated as expanding circles of active pixels beginning with a circle of radius 8 pixels and expanding at a rate of either 8 pixels per frame (fast looming) or four pixels per frame (slow looming). To compare the strength of activity modulation because of stimulus competition, the same simulations were performed with each stimulus presented alone at the same, respective, location (Fig. 5F,G, “single”). To better visualize activity modulations arising from stimulus competition, the output weights of the GI layer units () were scaled up by a factor of 10 for these simulations. The mean activity of the change detection output neurons representing a 250 × 250 patch, centered on the respective stimulus, is plotted in Figure 5F,G. All simulations in Figure 5 were performed with a partially trained model (checkpoint saved at n = 100 training iterations) to model the comparatively volatile mnemonic representations observed in biology.
Mimicking experimental effects of causal manipulations of SC/OT
We simulated the effect of SC/OT microstimulation on a common psychophysical change detection task (Cavanaugh and Wurtz, 2004; Zénon and Krauzlis, 2012). First, to simulate the orientation change detection task (Fig. 6A), we presented two gratings, one in each visual hemifield. Again, we tiled 50,000 st-RNN modules with 50% overlap along both x- and y-directions to encode the entire image (1000 × 800). Both gratings were presented at full contrast. The gratings were presented at random initial orientations (here, 20° and 135° clockwise of vertical for left hemifield and right hemifield stimuli respectively). This was followed by eight blank frames, following which the gratings reappeared for one frame. Upon reappearance the orientation of the grating in the left hemifiled alone changed to 30° (Fig. 6A, top right, red box). We expected the st-RNN output to identify the grating at this location alone as the “change,” whereas the actual output of the model produced false alarms at other locations also (Fig. 6A, bottom right). To mimic focal microstimulation of the SC/OT, we scaled up the recurrent and output weights (1.1 * Weff) of the mnemonic coding st-RNN units encoding the grating in the either the left (change) or right (no change) hemifield, respectively. Our default model was trained to the point where change detection and mnemonic coding were near perfect, and items were maintained for robustly for even the longest epochs (>200 time points) tested. On the other hand, mnemonic representations in biology are comparatively volatile (Goldman, 2009). To model this shortcoming, and to model its rescue with microstimulation, simulations in Figure 6A–C were performed with a partially trained model st-RNN model incorporating Eq. 4 (checkpoint saved at n = 100 training iterations) whose mnemonic representations decayed more rapidly compared with the fully trained model.
Change blindness experiments with human participants
A total of n = 44 participants (20 females; age range 18–55 years) with normal or corrected-to-normal vision performed a change blindness experiment (Jagatap et al., 2021). Data from four participants, who were unable to complete the task for various reasons, were excluded, as was data from one participant that was not stored correctly because of logistic errors. The final analyses were performed on data from 39 participants (18 females). Details of the change blindness experiment have been reported elsewhere (Jagatap et al., 2021).
Briefly, subjects viewed the images on a 19” Dell monitor (1024 × 768 resolution) seated with their heads resting on a chin rest, with their eyes positioned 60 cm from the monitor. Subjects' eye movements were tracked with an iViewX Hi-speed eye-tracker (SensoMotoric Instruments Inc.) with a sampling rate of 500 Hz; the tracker was calibrated for each subject, individually, before the start of the experiment. Each trial of the change blindness task comprised a pair of alternating images, each of 250-ms duration, separated by blank screens, also of 250-ms duration. Each trial began with subjects fixating continuously for 3 s on a central cross; this was done to ensure consistency in the first fixation across subjects. In each experiment, we tested either 26 or 27 pairs of images (Jagatap et al., 2021, their Fig. S1; Supplemental Data). Of these 20 image pairs contained at least one object that differed in key respects across the image pairs, in size, color or occurrence. The remaining six (n = 9 subjects) or seven (n = 30 subjects) image pairs were catch images that consisted of identical images with no distinction between them. Change and catch trials were interleaved in a pseudorandom order across all the subjects. For the analyses presented in this paper, we used only data from change image trials. Subjects were allowed to freely move their eyes across the scene to locate the change. They indicated correctly detecting the change by fixating on the change region for at least 3 s, and such trials were considered a “hit.” If the subjects failed to detect the change within 60 s, the trial timed-out and was considered a “miss.” Each session lasted for roughly 45 min, including time for instruction and eye-tracker calibration.
Change blindness experiments with the st-RNN model
To simulate the change blindness flicker paradigm (Fig. 7A), each image (A) and the corresponding altered version (A*) were displayed, along with interleaved blank images (B), each for two frames. This cycle was repeated until the model detected the change, or the maximum trial duration elapsed. In our experimental data, the maximum permitted time for human participants to detect the change was 60 s, and each image and blank were presented for 250 ms. To match these statistics, the maximum trial length of our model simulations was set to 240 frames, with each frame equivalent to an interval of 125 ms in the original experiment. The model was permitted to make saccades (gaze shifts, see next) at the end of every set of four frames starting with the fifth frame, such that saccades were made after every sequence of the form ABBA* or A*BBA; this intersaccade interval (fixation duration) of 500 ms approximately matches the mean fixation duration of ∼400 ms that we observed in data from human participants performing the change blindness task (Jagatap et al., 2021).
To simulate saccades in the change blindness task, we adopted the following procedure. First, we computed a priority map for saccades based on three different factors: (1) bottom-up saliency; (2) top-down task goals; (3) inhibition of return. The first and third components have been extensively investigated in previous studies, and are known to be important for determining free-viewing saccade strategies (Itti et al., 1998; Adeli et al., 2017). The second component (top-down goal) is specific to our task, in that participants must scan the image with the goal of identifying changes. We computed each of these factors as follows. First, the image Ai in physical image coordinates at frame i was CVR transformed to retinocentric coordinates, based on gaze fixation at location x (see above, Modeling change detection with high-resolution images). We term this transformed image as Ai,x. Next, the bottom up saliency map was computed from the Itti–Koch algorithm, also as described above (Itti et al., 1998). We term this real-valued map B(Ai,x). Then, the top-down goal map, or “change map,” was computed based on the activation of the output layer of the change-detection st-RNN; this corresponds to a map of the likely location(s) of change, as determined by the network. st-RNN modules were tiled to encode the entire image, and activations were averaged over these overlapping tiles to yield the final top-down map. This map was thresholded at 0.5 to yield a binary map. We term this “change” map T(Ai,x). Finally, the inhibition-of-return (IOR) map was computed by specifying a two-dimensional circularly symmetric Gaussian centered at the point of fixation, with a variance of 40 pixels, and summed over the past m = 50 fixations. This map was CVR transformed and normalized between 0 and 1 to yield the final IOR map, I(Ai,x). These three maps [B(Ai,x), T(Ai,x), I(Ai,x)] were combined to determine the final priority map, P(Ai,x), as follows:
| (13) |
| (14) |
where is a piecewise linear mapping, which saturates at a value of 1 for all arguments greater than 1.
As a final step, the priority map was normalized by its sum across all image locations, so as to transform it into a spatial probability density. The next fixation at each time point was sampled from this probability density function. To execute the fixation, the priority map was reverted to physical image coordinates using an “inverse CVR” transform, the new fixation location was selected and the image was transformed again into retinocentric coordinates with the CVR transform, based on the new gaze fixation point (Fig. 7B).
Comparing human and model gaze metrics
To compare gaze metrics of human participants with the model (Fig. 8B), we computed, for each of the 20 change images, the mean number of fixations, on “hit” trials, across n = 39 participants. We also computed the total distance traveled as sum of Euclidean distance (in pixels) between consecutive fixations. We then compared these human gaze metrics with the same metrics computed from model simulations using Pearson correlations; model metrics were computed by simulating the model for n = 80 iterations and computing the average over these iterations. As a control analysis, we performed these same correlations except that the st-RNN output, corresponding to the top-down component [T(Ai,x); Eq. 13] was excluded when computing the priority map. All other parameters were identical for these control simulations.
Comparing fixation predictions across models
We tested how our model would compare with other established algorithms for predicting human gaze fixations. For this, we computed a fixation map as a continuous map across the entire image from the distribution of discrete fixations by convolution with a Gaussian filter describe and applying a standard low-pass filter with cutoff frequency fc = 8 cycles per image (Bylinskii et al., 2019). For comparing performance across models, we tested various metrics, including those based on the correlation coefficient (CC), similarity, Kullback–Leibler (KL)-divergence and area under the curve (AUC). Previous studies on gaze prediction have suggested that multiple metrics should be used for comparing gaze prediction algorithms, because of different potential kinds of bias in each metric (Bylinskii et al., 2019). We briefly describe, below, these evaluation metrics. In the following, G denotes the fixation map obtained from human data, and S denotes the map estimated using a saliency prediction model.
Linear CC. The CC metric between G and S is given by: CC = cov(G, S)/(σG*σS), where σG and σS are the standard deviations of vectorized maps G and S respectively. This metric provides a measure of the linear relationship between the two maps, with a CC of +1 indicating a perfect linear relationship between the maps.
Similarity. Similarity is computed as the sum of the minimum values at each pixel location for the distributions of S and G. , where SN and GN are normalized to be probability distributions so that, for identical maps, the similarity score is +1.
KL-divergence. KL-divergence measures the difference between the two probability distributions S and G as , where is a regularization constant with value = 2.22 × 10−16 (Bylinskii et al., 2019).
AUC. The area under the receiver-operating-characteristic curve (AUC) is computed by thresholding the saliency map at varied values. The true positive (TP) and false positive (FP) proportions are computed at each of these threshold values, and the AUC is calculated. The AUC-Borji (Borji et al., 2013) algorithm defines the proportion of TPs as the number of the saliency map (S) pixels above threshold relative to the total number of fixated pixels in the image, and defines the proportion of FPs as the number of saliency map (S) pixels above threshold relative to a uniform random sample, equal to the number of nonfixated pixel locations.
The comparison of our eye movement model was performed against Salicon with the images used in our human change blindness experiment, and not with the MIT300 dataset. This is because we seek to test our model against ground-truth human fixation data in a change blindness task, whereas the MIT300 dataset is for free-viewing saliency prediction.
Data and code availability
Data and code for reproducing the results in this paper are available in the following repository: https://github.com/yashmrsawant/ChangeDetection_stRNN.
Results
A midbrain-inspired st-RNN model
The SC, and the OT, its homolog in other vertebrates, receives direct visual input from the retina and projects to cortical and subcortical regions involved in controlling attention and eye-movements (Knudsen, 2011; Krauzlis et al., 2013; Fig. 1A). Neurons in the SC/OT exhibit spatially restricted visual receptive fields with topographic connectivity: each neuron encodes only a portion of visual space (typically 5–10°; Cynader and Berman, 1972), and connects predominantly with downstream neurons that encode overlapping regions of space (Knudsen, 2011; Sridharan et al., 2014). In addition, the SC/OT is multilayered, comprising recurrently connected excitatory (E) and inhibitory (I) neural populations (Knudsen, 2018). In particular, layer 10 of the SC/OT contains specialized recurrent E-I neurons that project to a midbrain inhibitory (GABAergic) isthmic nucleus, the Imc (Fig. 1A; Goddard et al., 2012, 2014), which is hypothesized to play a key role in resolving stimulus competition across space (Knudsen, 2018; see next section).
We modeled the recurrent E-I circuit in SC/OT layer 10, employing a RNN with key neurobiological constraints (Fig. 1B). First, the input layer of the RNN was organized topographically, such that each patch of the input, in this case a high-resolution image, was represented by a localized patch of neurons, mimicking spatially localized retinal input to the SC. Second, following Dale's law for biological neurons, each presynaptic neuron in the model provided either excitatory or inhibitory inputs to all of its postsynaptic partners. Recurrent connections occurred both within and across E and I neural populations. Third, each neuron (both E and I) was permitted to connect to only to a small group of neurons in its neighborhood such that mutually connected neurons encoded overlapping regions of the image (Materials and Methods). This connectivity pattern ensured topographic connectivity, while also guaranteeing a sparse weight matrix for all layers (Fig. 1C; Materials and Methods, Eq. 1). We term such a RNN, with sparse, topographic connectivity, as an st-RNN. st-RNN dynamics were simulated with a phenomenological rate model, previously employed in simulations of neural population dynamics (Eq. 2, Materials and Methods; Ganguli and Latham, 2009; Sussillo, 2014). For illustration, we first describe the results of training and testing the st-RNN with simple, 8 × 8 binary image patches as input. In a subsequent section, we test the st-RNN's ability to detect changes in high-resolution, natural images.
Two key operations are necessary for solving the change blindness task (Fig. 1D). First, the network must robustly maintain a representation of the first image (Fig. 1D, A) over the duration of the blank frames (Fig. 1D, B). Second, this maintained information must be compared against the subsequently presented image (Fig. 1D, A*) for detecting and localizing the change successfully. These two operations were achieved with two different st-RNNs, operating in tandem (Fig. 1D). The first st-RNN, the “mnemonic coding” RNN, encoded and maintained the representation of the input image (A) over the duration of one or more blank frames (Fig. 1D). Moreover, this RNN learned to flexibly update its representation when presented with a new input image (A*) following the blank frames (Fig. 1D). The second st-RNN, the “change detection” RNN, monitored variations in output of the mnemonic-coding RNN, which enabled it to detect and localize the change (Fig. 1D). Both st-RNNs were trained independently, with 200,000 8 × 8 binary image patches, and tested with 20,000 validation patches, not used in the training dataset (Materials and Methods). We then compared the performance of the st-RNN against a conventional, fc-RNN, without constraints on sparse or topographic connectivity (Materials and Methods).
The st-RNN maintained its input and detected changes with high accuracy (Fig. 1E, top, blue; mean squared error or MSE: mnemonic coding st-RNN = 1.7 ± 0.02%, change detection st-RNN = 1.6 ± 0.02%, mean ± std at iteration 200; n = 20,000 validation patches). The fc-RNN's also detected changes with high accuracy (Fig. 1E, top, red; MSE: mnemonic coding fc-RNN = 2.6 ± 0.5%; change detection fc-RNN = 2.5 ± 0.1%), but the MSE for the fc-RNN was marginally, albeit significantly higher, as compared with the st-RNN (p < 10−6, n = 20,000 patches, Wilcoxon signed rank test). In addition, the fc-RNN training converged much more slowly (∼7.5–9× longer) both for the mnemonic-coding and change-detection operations (Fig. 1E, bottom, red vs blue curves; mnemonic-coding: st-RNN = 12 epochs, fc-RNN = 90 epochs; change-detection: st-RNN = 10 epochs, fc-RNN = 93 epochs; # iterations to achieve a training MSE of 1%, across 10,000 training samples). Moreover, the proportion of non-zero weights in the hidden layer of the fc-RNN (45.7%) was, far higher than the proportion of non-zero weights in the st-RNN (2.9%; Fig. 1F; p < 10−6; Kolmogorov–Smirnov test for significant differences in weight distributions).
We sought to understand the relative advantages of sparsity versus topographic connectivity for change detection. First, we asked whether the topographic nature of connectivity provided a specific advantage for change detection. We trained a network with random (nontopographic) connectivity, but with weight sparsity identical to the st-RNN; we call this network a sparse, non-topographic RNN (snt-RNN). The weight matrix following training is shown in Fig. 1F. The snt-RNN training converged more slowly (Fig. 1E, green) as compared with the st-RNN (Fig. 1E, blue). Specifically, the number of iterations for convergence (1% training MSE) was more than 2-fold higher for the snt-RNN as compared with the st-RNN (mnemonic-coding: st-RNN = 12 epochs, snt-RNN = 25 epochs; change-detection: st-RNN = 10 epochs, snt-RNN = 22 epochs). Second, we asked whether sparsity of the weight matrix was responsible for faster training. As an alternative model, we tested whether reducing the degrees of freedom, by reducing the number of weight updates, would also achieve faster training; for this, we applied a sparse mask (Materials and Methods, Eq. 1) to the gradient updates, rather than to the full weight matrix itself, during training. In this case, again we observed considerably slower convergence (Fig. 1E, black) as compared with the original st-RNN model (Fig. 1E, blue).
Finally, we performed simulations of the model by varying the level of sparsity in the connections, and with different sizes of local, topographic connections in the hidden layer (Fig. 1G; Materials and Methods). Increasing the level of sparsity led to systematic degradations in performance for both the mnemonic coding and change detection st-RNNs, likely because of the stronger constraints on connectivity imposed by progressively sparser weight matrices (Fig. 1H,I, columns). By contrast, decreasing the receptive field size degraded performance for the mnemonic coding st-RNN but slightly improved performance for the change detection st-RNN (Fig. 1H,I, rows). Because of its fine-grained, spatially local nature, the change detection computation was rendered more challenging when signals were pooled across multiple neighboring neurons.
In summary, our midbrain inspired st-RNN architecture was able to successfully solve the challenging change blindness task. Moreover, the st-RNN accomplished change detection far more efficiently, with considerably fewer connections and significantly faster learning rates, compared with a conventional, fc-RNN. Finally, neither a network with sparse, but unstructured, connectivity nor a network with a comparably simple, but a conceptually different, learning strategy were as fast as the st-RNN model at learning to successfully detect changes. In other words, both sparsity and topographic connectivity were relevant for efficiently learning to detect changes (see Discussion for caveats regarding the biological plausibility of the supervised learning rule).
Mechanisms underlying stable maintenance and flexible updating
We analyzed computational mechanisms by which the st-RNN achieves robust change detection in this change blindness task. The computation performed by the change detection st-RNN is a comparatively simple one: it needs to compute differences between each successive frame of the mnemonic coding st-RNN's output, as long as the latter maintains an active representation of the latest input. The key challenge, then, rests with the mnemonic coding st-RNN, which must not only maintain a stable representation of the first image (Fig. 1D, A) over the course of the blank epoch (Fig. 1D, B), but must also rapidly and flexibly update its representation as soon as the new image is presented (Fig. 1D, A*).
We analyzed, first, low-dimensional dynamics of the mnemonic coding st-RNN to understand how it was able to maintain image information robustly during the blank epoch. For this we identified a “mnemonic” subspace, based on the activity of the hidden layer units of the mnemonic coding st-RNN (Murray et al., 2017); the dimensions of this subspace represent those that capture maximal variance across stimuli during the blank epoch (stimulus PCs; Fig. 2A; Materials and Methods). We then plotted the activity trajectories of the hidden layer units in this mnemonic subspace (Fig. 2C, colored dots with connecting lines).
The mnemonic coding subspace encoded interpretable, and (partially) dissociable, features of stimuli during the stimulus presentation epoch: stimulus PC1 encoded the proportion of “active” pixels (sparsity) in the input image (Fig. 2A, x-axis, dark to light shading) whereas stimulus PC2 encoded the location of these active pixels – in terms of their approximate center of mass along the vertical axis (Fig. 2A, y-axis). Individual hidden layer units exhibited markedly heterogeneous dynamics during the maintenance epoch. Some units (Fig. 2B, top) exhibited stable activity during maintenance, whereas others (Fig. 2B, bottom) exhibited unstable and oscillatory patterns of activity. Despite these wide variations in individual unit dynamics, the projection of hidden layer activity in the mnemonic subspace was remarkably stable over time, even in the absence of sensory input (Fig. 2C; different colors show activity projection at different time points during the blank epoch). Dynamics were primarily confined to a “Time PC,” orthogonal to the stimulus PC axes (Fig. 2C, left; Materials and Methods). In other words, stable coding in the mnemonic subspace emerged despite heterogeneous dynamics in individual units' activities. Each of these characteristics is a hallmark of the “stable subspace model,” a recently proposed framework for stable maintenance of information in the brain (Druckmann and Chklovskii, 2012; Murray et al., 2017). In Materials and Methods, Stable network output despite unstable activity in individual units, we analyze these observations mathematically to show how a stable representation may arise in the network with unstable and heterogenous units (Druckmann and Chklovskii, 2012).
We explored the contributions of distinct groups of units, based on the stability of their activity profiles, to robust maintenance. Specifically, we asked whether only units with stable activity dynamics enabled robust maintenance or whether units with unstable dynamics were also involved. We grouped hidden layer units into two subsets based on the top (“stable” units) and bottom (“unstable” units) 5th percentiles (Fig. 3A) of activity variance during the maintenance epoch [Materials and Methods; maintenance epoch variance: stable units = (3.45 ± 1.5) × 10−5 a.u., unstable units = (2906 ± 820) × 10−5 a.u., n = 500 patterns]. Interestingly, while all of the stable units comprised excitatory neurons, a majority (11/16) of the unstable units comprised inhibitory neurons; connectivity kernels of representative stable and unstable excitatory neurons are shown in Figure 3B. Interestingly, as compared with unstable units, stable units exhibited a much sparser connectivity profile both in terms of the input and recurrent connections. By contrast, few unstable units contributed directly to the st-RNN output; most contributed only indirectly through recurrent connections.
We tested whether, and how much, each of these subsets (stable or unstable) contributed to stable maintenance. Silencing the stable subset alone produced a strong degradation of the maintained pattern (Fig. 3C, dark gray open circles, “Stable-”), as compared with when all units were intact (Fig. 3C, filled circles, “None”). On the other hand, silencing the unstable subset alone produced a weaker but, nevertheless, robust degradation of the maintained pattern (Fig. 3C, light gray open circles, “Unstable-”); surprisingly, this degradation increased progressively to even surpass the level of degradation following silencing the stable subset. This latter finding could be explained on the basis of the large proportion of inhibitory neurons (∼70%) in the unstable subset: silencing these neurons reduced network inhibition and resulted in runaway excitation because of which the maintained pattern degraded progressively. In Materials and Methods (see “Unstable” units are important for stable maintenance), we leverage an analytical framework for the stable subspace model (Wasmuht et al., 2018) to further analyze these results based on the null space of the feedforward (hidden to output) connectivity matrix.
Next, we asked which type(s) of recurrent connections in the mnemonic coding st-RNN were critical to stable maintenance. For this, we silenced, in turn, each type of recurrent connection in the hidden layer, separately, during the maintenance (blank) epochs (Fig. 3D, gray shading, t = 2–10 and t = 12–20) and calculated the mean error with pattern maintenance. We expected that silencing the E-E or I-I connections would decrease the overall excitation in the network, the latter by disinhibiting the inhibitory neurons (Sridharan and Knudsen, 2015), whereas silencing the E-I or I-E connections would decrease the overall inhibition in the network. We tested the effect of each of these manipulations on stable maintenance.
Silencing mutual E-E connections (Fig. 3D, green) or the mutual I-I connections (Fig. 3D, dark gray; virtually overlapping with the green curve) produced the strongest degradation of maintained patterns, as quantified by the mean error (L1 norm) relative to the expected output (higher error signifies more degradation). Silencing the other two connection types (I-E or E-I) also disrupted maintenance (Fig. 3D, blue and red, respectively), but these effects were marginally weaker. These results could be explained mechanistically. In the absence of external inputs during the blank, silencing recurrent E-E connections abolished the activity in the hidden layer E neurons and eliminated persistence, yielding in null activity in the output layer during the blank (Fig. 3F, E-E–). Similarly, silencing I-I connections abolished the recurrent inhibition to hidden layer I neurons. This resulted in over-strong inhibition of the E neurons, which abolished their activity and eliminated persistence, as before (Fig. 3F, I-I–). On the other hand, silencing E-I connections abolished inhibition in the network, thereby producing over-strong excitation in the E neurons. As recurrent E-E connections were intact the entire hidden layer became active after a few frames, and ultimately resulted in disrupted maintenance (Fig. 3F, E-I–). Silencing I-E connections also disrupted persistence but, interestingly, this disruption showed an oscillatory pattern (Fig. 3F, I-E–): removing the inhibitory input to E neurons resulted in their over-strong excitation, which, coupled with the intact E-I and I-I, shifted the network into an oscillatory regime (Tiesinga et al., 2004).
Finally, we asked which connections in the mnemonic coding st-RNN were critical to flexible updating, on presentation of the new input image (A*). Again, for this we silenced each type of recurrent connection in the hidden layer, transiently, when the new image was presented (Fig. 3E, gray shading at t = 11). In this case, silencing the I-E connections (I-E−; Fig. 3E, blue) or E-I connections (E-I−; Fig. 3E, red) produced the strongest degradation in flexible updating, which persisted throughout the subsequent maintenance epoch (Fig. 3E, t = 12–20). In contrast, silencing E-E or I-I connections resulted in no discernible degradation in flexible updating (Fig. 3E, green and dark gray, respectively). These effects could also be readily explained. Silencing I-E connections produced over-strong excitation of the E neurons, thereby yielding a degraded representation in the hidden layer when the new image was presented (Fig. 3G, I-E–). A similar effect occurred with silencing E-I connections because of transiently reduced inhibition in the network; in this case, the degradation was more modest because some excitation to the I neurons was provided directly by the feedforward input from the image patch (Fig. 3G, E-I–). In both cases (I-E– and E-I–), the degraded representation was maintained and amplified through recurrence over the subsequent blank epochs, because all connections were held intact during these epochs. In contrast, silencing E-E and I-I connections during the encoding, merely reduced the net recurrent excitation (directly or indirectly, respectively), whereas the dominant source of excitation to the hidden layer was from the input layer, which was held intact. Therefore, no obvious degradation of the representation was observed on silencing the E-E or I-I connections (Fig. 3G, E-E– and I-I–).
In summary, the mnemonic-coding st-RNN mimicked key hallmarks of the “stable subspace” model, a candidate model for working memory in the neocortex (Murray et al., 2017). Stable maintenance occurred despite marked heterogeneity in individual unit activities. Surprisingly, units with both stable and unstable dynamics contributed to robust maintenance of stored activity patterns. Connections that increased the excitatory tone in the network (E-E and I-I) were relatively more important for stable maintenance. In contrast, connections that increased the inhibitory tone in the network (I-E and E-I) were critical for flexible updating. The results suggest potentially dissociable roles of recurrent excitation and inhibition during change detection (Discussion).
A midbrain inspired GI motif promotes efficient change detection
Having achieved change detection in binary 8 × 8 image patches, we sought to test the model in a change blindness task with high-resolution, natural images (Fig. 4A, top). We encoded high-resolution (1024 × 768) images by tiling individual 8 × 8 st-RNN modules, along both horizontal and vertical axes, with 50% overlap between adjacent modules (49,152 modules total, Fig. 4A, bottom; Materials and Methods). Because midbrain SC neurons are known to encode visual saliency, the input to the st-RNN was a thresholded saliency map of each image (Fig. 4B, A and A*; Materials and Methods; Itti et al., 1998).
To our surprise, this “tiled” network, even after extensive training, failed to detect particular categories of changes consistently. While the network robustly detected the appearance of a novel object or feature in the new image (“off-on” changes), it consistently failed to detect disappearance of already present objects or features (“on-off” changes). For example, when a transition of the latter type occurred in the sequence shown in Figure 4B, the network failed to detect the disappearance of the “steel railing” (Fig. 4B, red box; model output, −GI).
To explain the reason for this failure we simulate the network with a “toy” example comprising nine 8 × 8 st-RNN modules tiled together in a 3 × 3 grid (24 × 24 neuron network; no overlap among modules; Fig. 4C). We replicated the failure case in this example: while the image patch that underwent an off-on change (Fig. 4C, first row, blue outline, appearance of the “kite” shape) was correctly detected (Fig. 4C, fifth row, −GI: CD, upper right patch), the patch that underwent an on-off change (Fig. 4C, first row, red outline, disappearance of the “plus” shape) failed to be detected (Fig. 4C, fifth row, −GI: CD, center patch). Examining the output of the mnemonic coding st-RNN revealed that the patch that underwent an on-off change continued to be maintained even on presentation of the new image, A* (Fig. 4C, fourth row, −GI: MC, center patch) and, therefore, was not flagged by the change detection st-RNN (Fig. 4C, fifth row, −GI: CD, center patch).
Why was the nonexistent stimulus erroneously maintained, even on presentation of the new image? We propose that each mnemonic-coding st-RNN module cannot, by itself, distinguish between on-off changes across the images (A, A*), versus transition from an image to a blank epoch (A to B). In other words, an isolated st-RNN module cannot distinguish between the following two scenarios: (1) when its input vanished because the new image contained a blank patch at the module's location (Fig. 4C, A*, center patch), versus (2) when its input vanished because of the blank epoch onset (Fig. 4C, B, center patch). Note that, in scenario (2), the mnemonic coding st-RNN must maintain the representation of the original image patch, whereas in scenario (1) it must update its output to a blank patch. The inability to distinguish these scenarios resulted in a failure of the st-RNN to correctly detect on-off changes.
We hypothesized that this failure occurred because independent st-RNN modules lacked cues about changes of global context (e.g., presentation of a new image). To overcome this failure, we tested two different approaches. First, we modeled local interactions among st-RNN modules, which would enable these modules to infer information about global context, in an emergent manner (Materials and Methods). We discovered that this approach barely ameliorated this issue (Fig. 4C, +Li, sixth and seventh rows).
An alternative approach, then, is to enable global contextual cues to be shared among all st-RNN modules. We looked to the anatomy of the midbrain SC/OT network for circuit motifs indicative of global interactions. Neurons in the SC project topographically to an adjacent nucleus, nucleus Imc, whose neurons project back to the SC/OT to provide global inhibition, spanning the entire SC/OT map (Knudsen, 2018; Fig. 1A). We tested whether incorporating a global inhibition motif, inspired by SC/OT-Imc architecture, would overcome change detection deficits in this tiled st-RNN network.
We modeled a GI layer of 10 × 8 neurons (Fig. 4A) that received low-dimensional input, mimicking convergent input from the input layer (Materials and Methods), and projected globally to both E and I neurons in st-RNN hidden layers (Fig. 4A, orange arrows). A single st-RNN module was retrained from scratch along with this GI layer (Materials and Methods) and the GI layer weights were replicated, globally, across all st-RNN modules. This strategy of tiling multiple st-RNN modules – involves learning a relatively small number of weights (∼105) while also permitting scaling up the model to detect changes in arbitrarily large images (see Discussion). By contrast, we estimate that training up a full 1024 × 768 st-RNN network would require learning a significantly larger number of weights (∼1012; Materials and Methods). In neurobiological terms, such a divide-and-conquer approach enables the network to learn to detect changes efficiently, with far fewer connections, compared with a network that learns over the entire image.
With the GI layer incorporated, the st-RNN network achieved successful detection of on-off changes (Fig. 4C; +GI, eighth and ninth rows). Plotting the mnemonic coding st-RNN hidden unit activity in the mnemonic subspace revealed accurate updating for both on-off (Fig. 4E, left, “plus” to “blank”) and off-on (Fig. 4E, left; “blank” to “kite” arrow) changes (solid arrow indicates successful update). In contrast, in the network without the GI layer, this updating did not happen correctly for the on-off change (Fig. 4D, left, dashed arrow); rather, the “plus” representation continued to persist even after the new image was presented (Fig. 4D, left, colored dots from t = 13–20). Examining the activity of randomly selected hidden layer units revealed that the GI layer enabled a reset in activity on presentation of the new image (Fig. 4E, right, +GI), which did not occur without the GI layer (Fig. 4E, right, −GI). When tested with high-resolution natural images, incorporating the GI layer allowed the st-RNN network to correctly detect disappearing objects also (Fig. 4B, last row, +GI, red box).
Lastly, we also trained a version of the model with recurrent, topographic connections from the hidden layer excitatory neurons of the mnemonic coding layer to the GI layer (recurrent E-I connections to GI layer; Materials and Methods; Fig. 4A, dashed connections); the goal was to mimic recurrent connections between the SC/OT and Imc that have been observed experimentally (Knudsen, 2018). This network was also able to detect changes well, albeit with marginally higher mean absolute error than the standard network (4% relative to the trained standard network over 20 maintenance epochs, average across 10,000 patterns).
To summarize: independent st-RNN modules, tiled to encode natural (high-resolution) images, failed to detect transitions involving object disappearance. Incorporating a global, inhibitory layer, inspired by the neural architecture of the SC/OT-Imc circuit, overcame this failure by enabling global contextual cues, regarding the appearance of the new image, to flexibly update st-RNN unit activity for accurate change detection.
Model mimics functional properties of the SC/OT network
The st-RNN's architecture was constrained by neuroanatomical connectivity in the midbrain, and trained to perform change detection, a key neural computation known to occur in the midbrain (Cavanaugh and Wurtz, 2004; Lovejoy and Krauzlis, 2010; Knudsen, 2018). We asked if, as a consequence, st-RNN model neurons would mimic known functional properties of SC/OT neurons. In addition, we tested whether previously reported effects of causal manipulation (microstimulation) of the SC on change detection could be mimicked by analogous manipulations of model neurons. These simulations were performed with the network with recurrent connections from the hidden layer excitatory neurons to the GI layer, to mimic recurrent connections between the SC/OT and Imc, as described in the previous section. Moreover, to model the relatively volatile mnemonic representations observed in biology, for these simulations we employed a partially trained model whose mnemonic representations were less robust than a fully trained model (Materials and Methods).
First, we examined the activity of output neurons in the change-detection st-RNN vis-à-vis known properties of stimulus-encoding in SC/OT neurons (Knudsen, 2018). Visual neurons in the SC are known to fire strongly in response to dynamic stimuli (e.g., moving or looming objects) rather than to static stimuli (Knudsen, 2011; White et al., 2017). We presented each of these stimulus types to the model, in turn, as 1000 × 800 images by tiling 50,000 8 × 8 st-RNN modules (Fig. 5A–D, insets; Materials and Methods).
st-RNN output neurons exhibited higher sensitivity for dynamic versus static inputs. When a static image was presented to the model for four successive frames, output neurons of the change-detection RNN were active briefly, at the onset of the image (Fig. 5A,E), but not subsequently. On the other hand, when a moving stimulus was presented neurons responded with a much higher steady state response (∼4×), as compared with when a static stimulus was presented (Fig. 5B,E). Similarly, when we presented a looming stimulus the neurons responded with an even higher steady state response (∼5× static stimulus' steady state response; Fig. 5C,E). Finally, neural responses to receding stimuli were also robust, albeit marginally weaker than those evoked by looming stimuli (Fig. 5D,E), qualitatively in line with recent experimental observations (Lee et al., 2020). The higher sensitivity of model neurons to dynamic, as compared with static, stimuli is an emergent consequence of training the network to detect changes and has interesting implications for understating the role of the SC in saliency computations (Discussion). In addition, the stronger response to looming, as compared with receding stimuli, was an emergent consequence of the interaction between the mnemonic and change-detection st-RNNs, providing an alternative to the mechanism proposed in an earlier experimental study (Lee et al., 2020; see Discussion).
Second, SC/OT neurons are known to exhibit robust signatures of stimulus competition: when multiple stimuli are presented concurrently, the strongest stimulus is represented preferentially, and suppresses responses to weaker stimuli (Mysore et al., 2010) To test whether these signatures of stimulus competition also emerged in our st-RNN model, we simulated paired looming stimuli, one looming fast, and the other comparatively slowly, one in each visual quadrant (Materials and Methods; Fig. 5F, inset). We observed clear signatures of competitive suppression in the activity of the change-detection st-RNN outputs: responses evoked by the weaker (slow looming) stimulus were markedly (∼8%) lower when it was paired with a stronger (fast looming) stimulus, than when it was presented by itself (Fig. 5F,H). By contrast, responses to the stronger (fast looming) stimulus were nearly identical, regardless of whether it was paired with a slow looming stimulus or presented alone (Fig. 5G,H). In other words, the st-RNN model exhibited clear, emergent evidence for stimulus competition.
Finally, we examined the model's performance in a perceptual change detection task vis-à-vis the known role of the SC/OT's in mediating change detection (Cavanaugh and Wurtz, 2004; Lovejoy and Krauzlis, 2010; Knudsen, 2018). Specifically, we simulated a visual change detection psychophysics task, commonly used in “change blindness” experiments in the laboratory (Steinmetz and Moore, 2014; Sridharan et al., 2017; Sagar et al., 2019; Banerjee et al., 2019). In this task, two oriented gratings are presented, one in each visual hemifield (Fig. 6A, set A). After a random delay, the screen is blanked, and gratings briefly disappear (Fig. 6A, blank B). Following reappearance, the orientation of one of the gratings has changed (Fig. 6A, set A*). The subject's task is to detect and localize the grating that changed in orientation.
To simulate this psychophysical task, as before, we represented the set of gratings as a 1000 × 800 image, by tiling 50,000 8 × 8 st-RNN modules (Materials and Methods). In this example, the grating in the left visual hemifield underwent an orientation change following the blank (“change” grating), whereas the right hemifield grating (“no-change” grating) remained unchanged (Fig. 6A, top row; red box). We employed the same partially trained st-RNN model as in the previous simulations. In this case, the model produced two types of errors: (1) signaling the change in the left hemifield grating (change grating) incompletely (compare Fig. 6A, left grating, Expected vs Observed), and (2) signaling a change in the right hemifield (no-change) grating also (“false-alarm”). Examining activity of the mnemonic coding st-RNN during the maintenance epoch revealed the reason for these errors: The maintained activity for original grating set (A) in both hemifields gradually deteriorated (Fig. 6A, second to last row) and, on presentation of the new grating set (A*), resulted in incorrect activations of the change detection units in both the change and no-change gratings (Fig. 6A, last row). As a consequence, the model signaled an incomplete change in the change grating, and a spurious change (false alarm) in the no-change grating.
We sought to rescue this deficit in the model by mimicking reported experimental effects of microstimulation of the SC/OT (Cavanaugh and Wurtz, 2004). In nonhuman primates focal microstimulation of the SC enhances the animals' ability to detect changes in a change blindness-like task (Cavanaugh and Wurtz, 2004). Specifically, SC microstimulation produces two key effects (see Cavanaugh and Wurtz, 2004; their Fig. 5B): (1) an improvement in change detection performance (hit rates) when microstimulation is applied to the target location (location of change), and (2) a decrease in false-alarms when microstimulation is applied to a nontarget location (location of no-change). We mimicked both of these effects of focal SC microstimulation in our model by scaling up (by 1.1×) the recurrent and output weights of mnemonic-coding st-RNN units at each, respective microstimulated location (Materials and Methods). Focal microstimulation of the right hemifield (no-change) grating representation produced a robust recovery of the network's ability to ignore this location without producing spurious activations (false-alarm; Fig. 6B,D, top). In contrast, focal microstimulation of the left hemifield (change) grating representation yielded accurate detection of the change in the left hemifield grating (compare Fig. 6A, Expected, left grating and C, Observed, left grating; Fig. 6D, bottom).
Taken together, these results suggest emergent similarities between st-RNN properties and biological properties of the SC/OT: not only did st-RNN model neurons resemble functional properties of SC/OT neurons in terms of their responses to dynamic (moving, looming, receding) and paired (competing) stimuli, but behavioral effects of SC/OT causal manipulations could also be reproduced with simulated manipulations of the st-RNN model. Our st-RNN model may, therefore, provide a test bed for understanding neural computations underlying change detection in the midbrain.
Model performance correlates with human performance in a change blindness task
Finally, we asked whether the st-RNN model would be relevant for understanding human performance in a change blindness task. For this, we analyzed data from 39 human participants performing a laboratory change blindness experiment with natural images (Materials and Methods; Jagatap et al., 2021). We summarize the task design here; details can be found in the previous study (Jagatap et al., 2021). On each trial a pair of images (cluttered scenes, typically) was alternately flashed for 250 ms, with an intervening blank, also of 250-ms duration (Fig. 7A). Subjects were instructed to detect the change by freely scanning the images. 20 image pairs were tested; each pair differed in terms of some key aspect (e.g., appearance or disappearance of an object; Materials and Methods). Subjects indicated the change location by fixating on it (for 3 s). If the change had not been detected within 60 s, the trial timed out.
We simulated gaze shifts on natural images with the st-RNN model by computing a “priority map” (Materials and Methods). Briefly, following foveal magnification (CVR; Wiebe and Basu, 1997), we computed a binarized saliency map, based on established algorithms (Itti et al., 1998; Otsu, 1979; Fig. 7B, left and top). This was provided as input to the st-RNN network, which produced a “change map” (Fig. 7B, rightmost). To encourage the model to explore the image thoroughly, we computed an IOR map (Materials and Methods), which discouraged saccades to previously fixated image locations (Materials and Methods). The final priority map was computed as a combination of the saliency map, the change map and the IOR map (Materials and Methods; Fig. 7B, lower right and bottom). Saccades were generated by constructing a probability density function over the image, whose value at each location was proportional to the priority at that location. The saccade generation process terminated when the model either correctly fixated at the location of the change, or until 120 time steps had elapsed (analogous to the human experiment).
Exemplar scan paths for the model and the human are shown in Figure 8A, red lines. We quantified the similarity of the model's gaze data with human gaze data using two approaches. First, we computed two gaze metrics: (1) the total number of fixations, and (2) the total “distance traveled” (cumulative path length of saccades), until the change was detected (Adeli et al., 2017), for both the human and model experiments. Strong correlations were observed between humans and the model, for both gaze metrics (Fig. 8B, number of fixations: r = 0.53, p = 0.017; total distance traveled: r = 0.55, p = 0.011; Pearson correlation). Because the priority map included a saliency component, we tested whether the correlations were driven primarily by the saliency (Itti et al., 1998), or whether they also required the change map (change detection st-RNN output). When we removed the change map from the priority map computation, correlations between the human and model gaze metrics were no longer significant (Fig. 8C, number of fixations: r = 0.31, p = 0.18; total distance traveled: r = 0.29, p = 0.217).
Second, we correlated human fixation maps with those generated by the st-RNN model. We compared this correlation against that generated by the “Salicon” saliency prediction algorithm (Huang et al., 2015), among the highest ranked algorithms in the MIT saliency benchmark leaderboard (Bylinskii et al., 2019) for predicting free-viewing fixation maps. We employed four standard benchmark metrics for comparing the similarity of fixation maps: AUC-Borji, KL-divergence, Similarity score and CC (for details, see Materials and Methods; Bylinskii et al., 2019). The st-RNN model significantly outperformed the state-of-the-art Salicon model, based on three out of the four benchmark metrics (Fig. 8D, signed rank test, across 20 image pairs). We also compared the st-RNN model's fixation map predictions with the conventional Itti–Koch saliency prediction algorithm and observed similar results (Fig. 8E).
In summary, st-RNN model gaze metrics resembled human gaze metrics in a laboratory change blindness experiment. Moreover, the st-RNN outperformed a state-of-the-art saliency prediction algorithm (Salicon) in terms of predicting human fixations. Thus, the st-RNN model may enable linking essential neural computations with psychophysical mechanisms underlying change detection in change blindness tasks.
Discussion
Detecting changes, across space and time, is a fundamental operation of the nervous system (Engel et al., 2001). Neurons in a variety of sensory cortical areas (Borst and Egelhaaf, 1989; Zatorre et al., 2002; Buonomano and Maass, 2009), are tuned to detecting and processing temporal gradients in incoming stimulus information. Yet, in “change blindness” tasks, detecting changes cannot be accomplished by computing temporal gradients alone. A more complex sequence of operations is necessary, including maintaining information in the form of a (transient) memory trace, and comparing incoming sensory information with this mnemonic representation. Our model of change blindness, therefore, sought inspiration from the SC, a midbrain structure, that is known to exhibit delay period activity during the maintenance of spatial information (Wurtz et al., 2001) and is also known to be causally involved in change blindness tasks (Cavanaugh and Wurtz, 2004).
The SC, and its homolog in nonmammalian vertebrates, the OT (Basso and May, 2017), are multilayered structures with distinct neural subtypes in the different layers. Neurons in the superficial layers of the SC/OT (SCs) are involved in the analysis of visual space (Veale et al., 2017), and respond to changes in visual stimulus properties such as size, luminance or color (Corbetta et al., 1991; Herman and Krauzlis, 2017). In particular, these neurons respond strongly to dynamic, as compared with static stimuli, and systematically encode the strength of such salient, dynamic stimuli (Knudsen, 2011, 2018). Our model neurons also exhibited enhanced sensitivity to moving and looming stimuli (Fig. 5). Remarkably, the sensitivity to motion or loom was not programmed into model neurons but emerged as a consequence of training the network to detect changes in static stimuli. Moreover, responses to looming stimuli were stronger than those evoked by receding stimuli, qualitatively resembling recent experimental observations (Lee et al., 2020). Whereas (Lee et al., 2020) modeled looming selectivity based on distinct dynamics of excitatory and inhibitory neurons, in our model, such selectivity arises from a different mechanism. Because of the mnemonic coding layer, activations of peripheral units for the receding (but not looming) stimuli persist marginally over successive frames (Fig. 5C,D, MC), thereby attenuating the output of the change detection units (Fig. 5C,D, CD). These results suggest that motion and loom sensitivity in the SC/OT may be an emergent property of more fundamental computations, information persistence at short timescales, and change detection.
Neurons in intermediate-deep layers of the SC/OT (SCi) project to other brain regions, as well as to oculomotor nuclei in the brainstem that control eye movements (Veale et al., 2017; Knudsen, 2018). Of particular interest are neurons in intermediate layer 10 of the vertebrate OT that contain recurrently connected excitatory and parvalbumin positive (PV+) inhibitory interneurons (Goddard et al., 2014). In the model, successful change detection relied on the ability to both maintain representation of the original stimulus stably during the blank epoch, and to update this representation flexibly on presentation of a novel stimulus. Our analysis (Fig. 3D–G) of the role of connection subtypes in the model revealed a double dissociation of excitation versus inhibition in mediating each of these functions (maintenance and updating, respectively). This hypothesis can be tested experimentally by targeted inactivation of each class of connections, those that increase the excitatory tone, versus those the increase the inhibitory tone of the network, in turn.
At first glance, modeling persistent sensory inputs in the SC appears at odds with previous experimental results, which report highly transient SC/OT responses following visual stimulation (Sridharan et al., 2011; Zhao et al., 2014; Lee et al., 2020). In our model recurrent excitatory connections among SCi neurons enable persistence of sensory input during the blank epoch. Yet, neurons in SCi/OTi layer 10 also provide topographic projections to a GABAergic midbrain nucleus, the Imc, which provides feedback global inhibition to the entire SC/OT representation (Wang et al., 2017). In our model, we incorporated a GI motif inspired by the neuroanatomy of this SC/OT-Imc circuit. In our model, activating the GI (Imc) input terminates the persistence of activity in the SC/OT (Fig. 4E). In other words, our model can operate in two modes: in the absence of GI (Imc) input, recurrent connectivity in the mnemonic coding st-RNN (SCi) enables persistent activity; this result mimics experimental findings that show robust persistent activity in an Imc-disconnected OT slice, in vitro (Goddard et al., 2012). Yet, when the GI layer (Imc) is activated, inhibition dominates and persistence is suppressed (Fig. 4E); this result mimics experimental findings in the SC in vivo, during natural visual stimulation, e.g. (Lee et al., 2020).
Activation (or deactivation) of the GI/Imc, therefore, provides a mechanism for flexibly turning “off” (or “on”) persistent activity in the SC. We propose that, by default, the Imc is active and this suppresses persistence and yields transient visual responses in the SC during sensory stimulation. Yet, when a task requires active maintenance in working memory, Imc output is rendered functionally ineffective, and this enables persistent activity in the SC. In our model, the Imc was rendered inactive during the blank epoch to enable persistence in the SC/OT. It is possible that in the brain Imc activation is suppressed through top-down mechanisms (e.g., forebrain input) to enable such persistence in the SC.
Moreover, the GI/Imc module broadcasts global contextual cues across the SC/OT input representation and facilitated effective change detection by enabling flexible updating when new inputs were presented to the network. While many other network motifs, such as global excitation or long-range recurrent connections, may serve to broadcast global contextual cues, our biologically inspired model provides a novel hypothesis regarding the role of the Imc in change detection. The Imc has been previously studied primarily for its role in spatial stimulus competition (Knudsen, 2011; Mysore and Knudsen, 2012). On the other hand, we propose that the Imc's GI output resolves temporal competition among input representations, such that old, irrelevant information can be effectively extinguished and novel, relevant information can take its place (Fig. 1A). Successful resolution of this temporal competition is essential to effective change detection, and our results suggest an experimentally testable role of the Imc in this key neural computation.
In the model, neurons in mnemonic coding st-RNN maintain information, in the form of a saliency map, during the blank interval. Previous experimental results suggest that a persistent saliency map could be present in the SC. First, recent experimental evidence suggests that SCs neurons encode a saliency map, with topographical activity representing each stimulus depending on its relative saliency (White et al., 2017). Second, SC neurons demonstrate persistent firing during the delay period of working memory tasks (Wurtz et al., 2001; Goddard et al., 2012; Rahmati et al., 2020); whether such persistent activity is linked entirely to premotor signals, or also carries sensory information, remains to be established. Even if high-dimensional persistent visual activity does not occur in the SC over the timescale of several seconds, it is conceivable that such persistence could occur over shorter timescales, of a few hundred milliseconds (e.g., ∼100–400 ms; Goddard et al., 2012), sufficient for stable visual representations to arise during the blank in the change blindness experiment. Another possibility is that mnemonic representations occur in a brain region distinct from the SC (e.g., in the associative cortices, or prefrontal cortex/PFC; Murray et al., 2017). In this latter case, objects at salient locations, as identified as such by the SCs, or other cortical regions (e.g., parietal cortex; Bisley and Goldberg, 2010), could be maintained in a prioritized state in the PFC. Top-down feedback from the PFC would then enable the SCi to implement change detection, which would, via the deep SC layers, subsequently drive gaze toward the next saccade target (Guerrasio et al., 2010). Simultaneous recordings from the SC and PFC, or association cortices, in the context of working memory tasks will permit disambiguating these hypotheses.
We demonstrated the relevance of the st-RNN model for change detection behavior, by simulating two experimental findings. First, we reproduced hallmark behavioral effects of causal manipulation of the SC on change detection. Causal experimental manipulations, such as microstimulation and pharmacological inactivation, have revealed a key role of the SC/OT in mediating target selection in the presence of distractors (McPeek et al., 2003; Carello and Krauzlis, 2004; Cavanaugh and Wurtz, 2004; Knudsen, 2011; Sridharan and Knudsen, 2015; Knudsen et al., 2017; Sridharan et al., 2017). Simulated microstimulation, by selectively enhancing the mnemonic coding st-RNN weights, improved the model's ability to detect changes and reduced the proportion of false alarms, in line with experimental effects (Cavanaugh and Wurtz, 2004). Second, we extended the model to incorporate saccades to simulate a laboratory change blindness experiment. The saccade priority map in our model included not only a “bottom-up” saliency map (Fig. 7B, left), but also a “goal-driven” map of task-relevant locations of change (“change map”; Fig. 7B, top right). In line with our model, converging evidence suggests that, in addition to coding for eye movements, neurons in the deep SC layers also represent task-relevant locations (McPeek et al., 2003; Carello and Krauzlis, 2004; Cavanaugh and Wurtz, 2004; Krauzlis et al., 2004; Hafed and Krauzlis, 2008; Knudsen, 2011; Sridharan and Knudsen, 2015). Notably, our st-RNN model with saccades outperformed a state-of-the-art algorithm (Salicon; Huang et al., 2015) with predicting gaze fixations in human participants performing a change blindness task. Saliency-based algorithms like Salicon (or Itti–Koch; Itti et al., 1998) are typically tuned for predicting gaze fixations in free-viewing tasks. Our results suggest that fixation strategies during change blindness tasks may be different from those during free-viewing tasks, and our model provides a starting point for investigating mechanisms underlying these differences in gaze strategies.
More generally, our results suggest three organizing principles that may underlie change detection in the brain. First, the st-RNN model, with sparse, local connectivity, learned significantly faster and achieved state-of-the-art change detection performance with far fewer connections than both a conventional, fc-RNN and an RNN with sparse, but unstructured (nonlocal) connectivity. These results suggest that topographic, local connectivity and structured organization, reported in neurons in various sensory (Ledoux et al., 1987) and higher-order brain regions (Shipp, 2004) may reflect an efficient architecture for implementing change detection, or similarly “local” neural computations. Such sparse, local connectivity reduces both the number of synapses (connections) as well as the length of wiring between computational units. Second, although the st-RNN was inspired by well-characterized neuroanatomical circuits in the SC/OT, the model architecture, comprising recurrently connected E-I neurons, represent a circuit motif that likely occurs in various brain regions, including the prefrontal cortex (Thompson and Bichot, 2005) and parietal cortex (Bisley and Goldberg, 2010). Thus, change detection may reflect the outcome of neural computations by recurrent E-I circuits that occur in parallel across several brain networks. Third, the model was able to effectively detect changes in high-resolution images (∼1024 × 768), although individual st-RNN modules were trained with no larger than 8 × 8 image patches (Fig. 4B). This success of this scaling depended on incorporating a global inhibition (GI) layer, that enabled global contextual information to be shared across independent st-RNN modules. In fact, training with multiple independent 8 × 8 modules and a single 10 × 8 GI layer required learning only a few ten thousand connection weights. By contrast, training a full 1024 × 768 st-RNN network would require learning several orders of magnitude more weights (∼). Scaling up functionality, based on learning in local modules (e.g., cortical columns, or columns in the SC/OT), coordinated by a global contextual signal (e.g., neuromodulation from the brainstem, or global inhibition from the Imc), could be a key principle by which the brain implements key neural computations, including change detection, at scale.
We propose a few modifications and extensions that could render the st-RNN model more biologically plausible. First, more detailed aspects of afferent and recurrent SC connectivity could be incorporated into the model. In the present model, inputs to the st-RNN are analogous to retinal afferents that synapse onto SC superficial layer neurons. Nevertheless, in addition to direct retinal inputs, the SC superficial layer neurons receive input from the visual cortex (Wurtz, 2009). Moreover, intermediate/deep layer neurons of the SC also receive inputs from forebrain regions including the lateral intraparietal area (LIP) and frontal eye field (FEF), as well as from the basal ganglia nucleus, substantia nigra pars reticulata (SNr; Francois et al., 1984). As we have speculated above, inputs originating in the visual cortex, LIP or FEF could be, at least partly, responsible for the delay period activity observed in the SC. On the other hand, in addition to its well-documented role in eye movement control (Hikosaka and Wurtz, 1983), inhibitory input from visual neurons in the SNr could help curtail the persistence of SC activity. Furthermore, modeling distinct neural types in the SC, including those subtypes linked to approach or avoidance behaviors (Shang et al., 2015; Evans et al., 2018; Hoy et al., 2019), as well as more refined modeling of lateral inhibitory interactions in the superficial and deep SC (Phongphanphanee et al., 2014; Whyland et al., 2020; Essig et al., 2021) will enhance the model's biological plausibility. Second, it is unclear whether the backpropagation algorithm used for training st-RNN network weights can be instantiated in biological networks (Zipser and Andersen, 1988; Stork, 1989). Nevertheless, recent studies have proposed biologically plausible implementations that are as effective as conventional backpropagation (Lillicrap et al., 2016; Neftci and Averbeck, 2019; Payeur et al., 2021); these modified algorithms can be incorporated when training our st-RNN modules. More generally, training the st-RNN network to detect changes with supervised learning approaches is likely far removed from how such networks are configured in biology. Future work involving unsupervised, or weakly supervised learning approaches that are also informed by known experimental facts on developmental programs that shape wiring in the SC/OT (Stein and Stanford, 2013), may render the st-RNN model more biologically plausible. Third, the activation functions of the st-RNN model neurons represent, at best, approximations to neural firing rates. Replacing st-RNN modules with spiking neural networks may render the model more biologically plausible. Fourth, the model was provided a saliency map as input (Itti et al., 1998) without addressing the biological origins of this map, although recent evidence suggests that superficial layer SC neurons encode stimulus saliency (White et al., 2017). Fifth, the mnemonic coding and change detection computations were achieved with distinct st-RNN networks. While it remains to be shown whether this exact sequence of operations also occurs in the midbrain, future extensions could model these operations in a single network with more efficient, training strategies. A possible extension along these lines is the ConvRNN model framework (Nayebi et al., 2018). This model combines specialized RNN cells with feedforward convolutional filters and long-range feedback and could be used to model the mnemonic-coding and change-detection operations in a single, unified model. Sixth, it is possible that other neurobiological mechanisms, such as repetition suppression, may be involved in change detection in the SC. Nonetheless, neurobiological evidence for a persistent representation in the SC (Wurtz et al., 2001; Goddard et al., 2014) suggests that a persistence based change detection mechanism is not implausible. Finally, our model detects particular kinds of changes (onset, offset or size changes) effectively. To detect other types of changes, such as changes of color, other saliency algorithms, such as the frequency tuned salient region detection algorithm (Achanta et al., 2009), may be incorporated into the model. Notwithstanding the scope for improvement, our study shows that RNNs, constrained by biological principles, provide a useful test bed for understanding neural computations, and their link with psychophysical mechanisms, underlying high-level cognitive phenomena.
Footnotes
This work was supported by a CSIR Ph.D. Fellowship (J.N.K.) and a Wellcome Trust-Department of Biotechnology India Alliance Intermediate fellowship, a Science and Engineering Research Board Early Career award, a Pratiksha Trust Young Investigator award, a Department of Biotechnology-Indian Institute of Science Partnership Program grant, a Sonata Software grant, and an India-Trento Program for Advanced Research grant (all to D.S.). We thank Srinivas Kumar and Simran Purokayastha for assistance with data acquisition and analyses and Guruprasath Gurusamy for help with preparing figures.
The authors declare no competing financial interests.
References
- Abadi M, Barham P, Chen J, Chen Z, Davis A (2016) Tensorflow: a system for large-scale machine learning. In: Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation. ACM. Available at https://dl.acm.org/doi/10.5555/3026877.3026899. [Google Scholar]
- Achanta R, Hemami S, Estrada F, Susstrunk S (2009) Frequency-tuned salient region detection. In: 2009 IEEE Conference on Computer Vision and Pattern Recognition, IEEE, pp 1597–1604. IEEE. Available at 10.1109/CVPR.2009.5206596. [DOI] [Google Scholar]
- Adeli H, Vitu F, Zelinsky GJ (2017) A model of the superior colliculus predicts fixation locations during scene viewing and visual search. J Neurosci 37:1453–1467. 10.1523/JNEUROSCI.0825-16.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banerjee S, Grover S, Sridharan D (2019) Unraveling causal mechanisms of top-down and bottom-up visuospatial attention with non-invasive brain stimulation. J Indian Inst Sci 97:451–475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barker AJ, Helmbrecht TO, Grob AA, Baier H (2021) Functional, molecular and morphological heterogeneity of superficial interneurons in the larval zebrafish tectum. J Comp Neurol 529:2159–2175. [DOI] [PubMed] [Google Scholar]
- Basso MA, May PJ (2017) Circuits for action and cognition: a view from the superior colliculus. Annu Rev Vis Sci 3:197–226. 10.1146/annurev-vision-102016-061234 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck DM, Rees G, Frith CD, Lavie N (2001) Neural correlates of change detection and change blindness. Nat Neurosci 4:645–650. 10.1038/88477 [DOI] [PubMed] [Google Scholar]
- Bisley JW, Goldberg ME (2010) Attention, intention, and priority in the parietal lobe. Annu Rev Neurosci 33:1–21. 10.1146/annurev-neuro-060909-152823 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borji A, Sihite DN, Itti L (2013) Quantitative analysis of human-model agreement in visual saliency modeling: a comparative study. IEEE Trans Image Process 22:55–69. 10.1109/TIP.2012.2210727 [DOI] [PubMed] [Google Scholar]
- Borst A, Egelhaaf M (1989) Principles of visual motion detection. Trends Neurosci 12:297–306. 10.1016/0166-2236(89)90010-6 [DOI] [PubMed] [Google Scholar]
- Buonomano DV, Maass W (2009) State-dependent computations: spatiotemporal processing in cortical networks. Nat Rev Neurosci 10:113–125. 10.1038/nrn2558 [DOI] [PubMed] [Google Scholar]
- Bylinskii Z, Judd T, Oliva A, Torralba A, Durand F (2019) What do different evaluation metrics tell us about saliency models? IEEE Trans Pattern Anal Mach Intell 41:740–757. 10.1109/TPAMI.2018.2815601 [DOI] [PubMed] [Google Scholar]
- Carello CD, Krauzlis RJ (2004) Manipulating intent: evidence for a causal role of the superior colliculus in target selection. Neuron 43:575–583. 10.1016/j.neuron.2004.07.026 [DOI] [PubMed] [Google Scholar]
- Cavanaugh J, Wurtz RH (2004) Subcortical modulation of attention counters change blindness. J Neurosci 24:11236–11243. 10.1523/JNEUROSCI.3724-04.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavanaugh J, Alvarez BD, Wurtz RH (2006) Enhanced performance with brain stimulation: attentional shift or visual cue? J Neurosci 26:11347–11358. 10.1523/JNEUROSCI.2376-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comoli E, Coizet V, Boyes J, Bolam JP, Canteras NS, Quirk RH, Overton PG, Redgrave P (2003) A direct projection from superior colliculus to substantia nigra for detecting salient visual events. Nat Neurosci 6:974–980. 10.1038/nn1113 [DOI] [PubMed] [Google Scholar]
- Corbetta M, Miezin FM, Dobmeyer S, Shulman GL, Petersen SE (1991) Selective and divided attention during visual discriminations of shape, color, and speed: functional anatomy by positron emission tomography. J Neurosci 11:2383–2402. 10.1523/JNEUROSCI.11-08-02383.1991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cynader M, Berman N (1972) Receptive-field organization of monkey superior colliculus. J Neurophysiol 35:187–201. 10.1152/jn.1972.35.2.187 [DOI] [PubMed] [Google Scholar]
- Druckmann S, Chklovskii DB (2012) Neuronal circuits underlying persistent representations despite time varying activity. Curr Biol 22:2095–2103. 10.1016/j.cub.2012.08.058 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel AK, Fries P, Singer W (2001) Dynamic predictions: oscillations and synchrony in top-down processing. Nat Rev Neurosci 2:704–716. 10.1038/35094565 [DOI] [PubMed] [Google Scholar]
- Essig J, Hunt JB, Felsen G (2021) Inhibitory neurons in the superior colliculus mediate selection of spatially-directed movements. Commun Biol 4:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans DA, Stempel AV, Vale R, Ruehle S, Lefler Y, Branco T (2018) A synaptic threshold mechanism for computing escape decisions. Nature 558:590–594. 10.1038/s41586-018-0244-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francois C, Percheron G, Yelnik J (1984) Localization of nigrostriatal, nigrothalamic and nigrotectal neurons in ventricular coordinates in macaques. Neuroscience 13:61–76. 10.1016/0306-4522(84)90259-8 [DOI] [PubMed] [Google Scholar]
- Gaillard F (1990) Visual units in the central nervous system of the frog. Comp Biochem Physiol A Physiol 96:357–371. 10.1016/0300-9629(90)90097-C [DOI] [PubMed] [Google Scholar]
- Ganguli S, Latham P (2009) Feedforward to the past: the relation between neuronal connectivity, amplification, and short-term memory. Neuron 61:499–501. 10.1016/j.neuron.2009.02.006 [DOI] [PubMed] [Google Scholar]
- Gibbs R, Davies G, Chou S (2016) A systematic review on factors affecting the likelihood of change blindness. Crime Psychol Rev 2:1–21. 10.1080/23744006.2016.1228799 [DOI] [Google Scholar]
- Goddard CA, Sridharan D, Huguenard JR, Knudsen EI (2012) Gamma oscillations are generated locally in an attention-related midbrain network. Neuron 73:567–580. 10.1016/j.neuron.2011.11.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goddard CA, Huguenard J, Knudsen E (2014) Parallel midbrain microcircuits perform independent temporal transformations. J Neurosci 34:8130–8138. 10.1523/JNEUROSCI.4399-13.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman MS (2009) Memory without feedback in a neural network. Neuron 61:621–634. 10.1016/j.neuron.2008.12.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guerrasio L, Quinet J, Büttner U, Goffart L (2010) Fastigial oculomotor region and the control of foveation during fixation. J Neurophysiol 103:1988–2001. 10.1152/jn.00771.2009 [DOI] [PubMed] [Google Scholar]
- Hafed ZM, Krauzlis RJ (2008) Goal representations dominate superior colliculus activity during extrafoveal tracking. J Neurosci 28:9426–9439. 10.1523/JNEUROSCI.1313-08.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heap LAL, Vanwalleghem G, Thompson AW, Favre-Bulle IA, Scott EK (2018) Luminance changes drive directional startle through a thalamic pathway. Neuron 99:293–301.e4. 10.1016/j.neuron.2018.06.013 [DOI] [PubMed] [Google Scholar]
- Herman JP, Krauzlis RJ (2017) Color-change detection activity in the primate superior colliculus. eNeuro 4:ENEURO.0046-17.2017. 10.1523/ENEURO.0046-17.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hikosaka O, Wurtz RH (1983) Visual and oculomotor functions of monkey substantia nigra pars reticulata. III. Memory-contingent visual and saccade responses. J Neurophysiol 49:1268–1284. 10.1152/jn.1983.49.5.1268 [DOI] [PubMed] [Google Scholar]
- Hoy JL, Bishop HI, Niell CM (2019) Defined cell types in superior colliculus make distinct contributions to prey capture behavior in the mouse. Curr Biol 29:4130–4138.e5. 10.1016/j.cub.2019.10.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang X, Shen C, Boix X, Zhao Q (2015) SALICON: reducing the semantic gap in saliency prediction by adapting deep neural networks. In: Proceedings of the IEEE International Conference on Computer Vision, pp 262–270. [Google Scholar]
- Itti L, Koch C, Niebur E (1998) A model of saliency-based visual attention for rapid scene analysis. IEEE Trans Pattern Anal Machine Intell 20:1254–1259. 10.1109/34.730558 [DOI] [Google Scholar]
- Jagatap A, Purokayastha S, Jain H, Sridharan D (2021) Neurally-constrained modeling of human gaze strategies in a change blindness task. PLoS Comput Biol 17:e1009322. 10.1371/journal.pcbi.1009322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingma DP, Ba J (2015) Adam: a method for stochastic optimization. In: 3rd International Conference for Learning Representations. arXiv 1412.6980. [Google Scholar]
- Knudsen EI (2011) Control from below: the role of a midbrain network in spatial attention. Eur J Neurosci 33:1961–1972. 10.1111/j.1460-9568.2011.07696.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knudsen EI (2018) Neural circuits that mediate selective attention: a comparative perspective. Trends Neurosci 41:789–805. 10.1016/j.tins.2018.06.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knudsen EI, Schwarz JS, Knudsen PF, Sridharan D (2017) Space-specific deficits in visual orientation discrimination caused by lesions in the midbrain stimulus selection network. Curr Biol 27:2053–2064.e5. 10.1016/j.cub.2017.06.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krauzlis RJ, Liston D, Carello CD (2004) Target selection and the superior colliculus: goals, choices and hypotheses. Vision Res 44:1445–1451. 10.1016/j.visres.2004.01.005 [DOI] [PubMed] [Google Scholar]
- Krauzlis RJ, Lovejoy LP, Zénon A (2013) Superior colliculus and visual spatial attention. Annu Rev Neurosci 36:165–182. 10.1146/annurev-neuro-062012-170249 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ledoux JE, Ruggiero DA, Forest R, Stornetta R, Reis DJ (1987) Topographic organization of convergent projections to the thalamus from the inferior colliculus and spinal cord in the rat. J Comp Neurol 264:123–146. 10.1002/cne.902640110 [DOI] [PubMed] [Google Scholar]
- Lee KH, Tran A, Turan Z, Meister M (2020) The sifting of visual information in the superior colliculus. Elife 9:e50678. 10.7554/eLife.50678 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lillicrap TP, Cownden D, Tweed DB, Akerman CJ (2016) Random synaptic feedback weights support error backpropagation for deep learning. Nat Commun 7:13276. 10.1038/ncomms13276 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu YJ, Wang Q, Li B (2011) Neuronal responses to looming objects in the superior colliculus of the cat. Brain Behav Evol 77:193–205. 10.1159/000327045 [DOI] [PubMed] [Google Scholar]
- Lovejoy LP, Krauzlis RJ (2010) Inactivation of primate superior colliculus impairs covert selection of signals for perceptual judgments. Nat Neurosci 13:261–266. 10.1038/nn.2470 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mastrogiuseppe F, Ostojic S (2018) Linking connectivity, dynamics, and computations in low-rank recurrent neural networks. Neuron 99:609–623.e29. 10.1016/j.neuron.2018.07.003 [DOI] [PubMed] [Google Scholar]
- McPeek RM, Han JH, Keller EL (2003) Competition between saccade goals in the superior colliculus produces saccade curvature. J Neurophysiol 89:2577–2590. 10.1152/jn.00657.2002 [DOI] [PubMed] [Google Scholar]
- Murray JD, Bernacchia A, Roy NA, Constantinidis C, Romo R, Wang XJ (2017) Stable population coding for working memory coexists with heterogeneous neural dynamics in prefrontal cortex. Proc Natl Acad Sci U S A 114:394–399. 10.1073/pnas.1619449114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mysore SP, Knudsen EI (2012) Reciprocal inhibition of inhibition: a circuit motif for flexible categorization in stimulus selection. Neuron 73:193–205. 10.1016/j.neuron.2011.10.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mysore SP, Asadollahi A, Knudsen EI (2010) Global inhibition and stimulus competition in the owl optic tectum. J Neurosci 30:1727–1738. 10.1523/JNEUROSCI.3740-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nayebi A, Bear D, Kubilius J, Kar K (2018) Task-driven convolutional recurrent models of the visual system. Adv Neural Inf Process Syst 31. [Google Scholar]
- Neftci EO, Averbeck BB (2019) Reinforcement learning in artificial and biological systems. Nat Mach Intell 1:133–143. 10.1038/s42256-019-0025-4 [DOI] [Google Scholar]
- Orhan AE, Ma WJ (2019) A diverse range of factors affect the nature of neural representations underlying short-term memory. Nat Neurosci 22:275–283. 10.1038/s41593-018-0314-y [DOI] [PubMed] [Google Scholar]
- Otsu N (1979) A threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern 9:62–66. 10.1109/TSMC.1979.4310076 [DOI] [Google Scholar]
- Pandarinath C, O'Shea DJ, Collins J, Jozefowicz R, Stavisky SD, Kao JC, Trautmann EM, Kaufman MT, Ryu SI, Hochberg LR, Henderson JM, Shenoy KV, Abbott LF, Sussillo D (2018) Inferring single-trial neural population dynamics using sequential auto-encoders. Nat Methods 15:805–815. 10.1038/s41592-018-0109-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paré M, Wurtz RH (2001) Progression in neuronal processing for saccadic eye movements from parietal cortex area lip to superior colliculus. J Neurophysiol 85:2545–2562. 10.1152/jn.2001.85.6.2545 [DOI] [PubMed] [Google Scholar]
- Pascanu R, Mikolov T, Bengio Y (2013) On the difficulty of training recurrent neural networks. In: International Conference on Machine Learning, pp 1310–1318. Available at http://proceedings.mlr.press/v28/pascanu13.pdf. [Google Scholar]
- Payeur A, Guerguiev J, Zenke F, Richards BA, Naud R (2021) Burst-dependent synaptic plasticity can coordinate learning in hierarchical circuits. Nat Neurosci 24:1010–1019. 10.1038/s41593-021-00857-x [DOI] [PubMed] [Google Scholar]
- Pessoa L, Ungerleider LG (2004) Neural correlates of change detection and change blindness in a working memory task. Cereb Cortex 14:511–520. 10.1093/cercor/bhh013 [DOI] [PubMed] [Google Scholar]
- Phongphanphanee P, Marino RA, Kaneda K, Yanagawa Y, Munoz DP, Isa T (2014) Distinct local circuit properties of the superficial and intermediate layers of the rodent superior colliculus. Eur J Neurosci 40:2329–2343. 10.1111/ejn.12579 [DOI] [PubMed] [Google Scholar]
- Port NL, Wurtz RH (2003) Sequential activity of simultaneously recorded neurons in the superior colliculus during curved saccades. J Neurophysiol 90:1887–1903. 10.1152/jn.01151.2002 [DOI] [PubMed] [Google Scholar]
- Rahmati M, DeSimone K, Curtis CE, Sreenivasan KK (2020) Spatially specific working memory activity in the human superior colliculus. J Neurosci 40:9487–9495. 10.1523/JNEUROSCI.2016-20.2020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reddy L, Quiroga RQ, Wilken P, Koch C, Fried I (2006) A single-neuron correlate of change detection and change blindness in the human medial temporal lobe. Curr Biol 16:2066–2072. 10.1016/j.cub.2006.08.064 [DOI] [PubMed] [Google Scholar]
- Rensink RA, O'Regan JK, Clark JJ (1997) To see or not to see: the need for attention to perceive changes in scenes. Psychol Sci 8:368–373. 10.1111/j.1467-9280.1997.tb00427.x [DOI] [Google Scholar]
- Sagar V, Sengupta R, Sridharan D (2019) Dissociable sensitivity and bias mechanisms mediate behavioral effects of exogenous attention. Sci Rep 9:12657. 10.1038/s41598-019-42759-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shang C, Liu Z, Chen Z, Shi Y, Wang Q, Liu S, Li D, Cao P (2015) A parvalbumin-positive excitatory visual pathway to trigger fear responses in mice. Science 348:1472–1477. [DOI] [PubMed] [Google Scholar]
- Shipp S (2004) The brain circuitry of attention. Trends Cogn. Sci 8:223–230. 10.1016/j.tics.2004.03.004 [DOI] [PubMed] [Google Scholar]
- Song HF, Yang GR, Wang X-J (2016) Training excitatory-inhibitory recurrent neural networks for cognitive tasks: a simple and flexible framework. PLoS Comput Biol 12:e1004792. 10.1371/journal.pcbi.1004792 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sridharan D, Knudsen EI (2015) Selective disinhibition: a unified neural mechanism for predictive and post hoc attentional selection. Vision Res 116:194–209. 10.1016/j.visres.2014.12.010 [DOI] [PubMed] [Google Scholar]
- Sridharan D, Boahen K, Knudsen EI (2011) Space coding by gamma oscillations in the barn owl optic tectum. J Neurophysiol 105:2005–2017. 10.1152/jn.00965.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sridharan D, Schwarz JS, Knudsen EI (2014) Selective attention in birds. Curr Biol 24:R510–R513. 10.1016/j.cub.2013.12.046 [DOI] [PubMed] [Google Scholar]
- Sridharan D, Steinmetz NA, Moore T, Knudsen EI (2017) Does the superior colliculus control perceptual sensitivity or choice bias during attention? Evidence from a multialternative decision framework. J Neurosci 37:480–511. 10.1523/JNEUROSCI.4505-14.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein BE, Stanford TR (2013) Development of the superior colliculus/optic tectum. In: Neural circuit development and function in the brain (Rubenstein JL and Rakic P, eds), pp 41–59. Oxford: Academic Press. [Google Scholar]
- Steinmetz NA, Moore T (2014) Eye movement preparation modulates neuronal responses in area V4 when dissociated from attentional demands. Neuron 83:496–506. 10.1016/j.neuron.2014.06.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stork (1989) Is backpropagation biologically plausible? In: International Joint Conference on Neural Networks, Vol2, pp 241–246, IEEE. Available at 10.1109/IJCNN.1989.118705. [DOI] [Google Scholar]
- Sussillo D (2014) Neural circuits as computational dynamical systems. Curr Opin Neurobiol 25:156–163. 10.1016/j.conb.2014.01.008 [DOI] [PubMed] [Google Scholar]
- Sussillo D, Barak O (2013) Opening the black box: low-dimensional dynamics in high-dimensional recurrent neural networks. Neural Comput 25:626–649. 10.1162/NECO_a_00409 [DOI] [PubMed] [Google Scholar]
- Sussillo D, Nuyujukian P, Fan JM, Kao JC, Stavisky SD, Ryu S, Shenoy K (2012) A recurrent neural network for closed-loop intracortical brain-machine interface decoders. J Neural Eng 9:026027. 10.1088/1741-2560/9/2/026027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson KG, Bichot NP (2005) A visual salience map in the primate frontal eye field. Prog Brain Res 147:251–262. [DOI] [PubMed] [Google Scholar]
- Tiesinga PH, Fellous J-M, Salinas E, José JV, Sejnowski TJ (2004) Inhibitory synchrony as a mechanism for attentional gain modulation. J Physiol Paris 98:296–314. 10.1016/j.jphysparis.2005.09.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tse PU (2004) Mapping visual attention with change blindness: new directions for a new method. Cogn Sci 28:241–258. 10.1207/s15516709cog2802_6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veale R, Hafed ZM, Yoshida M (2017) How is visual salience computed in the brain? Insights from behaviour, neurobiology and modelling. Philos Trans R Soc Lond B Biol Sci 372:20160113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Zorio DAR, Karten HJ (2017) Heterogeneous organization and connectivity of the chicken auditory thalamus (Gallus gallus). J Comp Neurol 525:3044–3071. 10.1002/cne.24262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wasmuht DF, Spaak E, Buschman TJ, Miller EK, Stokes MG (2018) Intrinsic neuronal dynamics predict distinct functional roles during working memory. Nat Commun 9:3499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White BJ, Munoz DP (2017) Neural mechanisms of saliency, attention, and orienting. In: Computational and cognitive neuroscience of vision, pp 1–23. Singapore: Springer. [Google Scholar]
- White BJ, Berg DJ, Kan JY, Marino RA, Itti L, Munoz DP (2017) Superior colliculus neurons encode a visual saliency map during free viewing of natural dynamic video. Nat Commun 8:14263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whyland KL, Slusarczyk AS, Bickford ME (2020) GABAergic cell types in the superficial layers of the mouse superior colliculus. J Comp Neurol 528:308–320. 10.1002/cne.24754 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiebe KJ, Basu A (1997) Modelling ecologically specialized biological visual systems. Pattern Recognition 30:1687–1703. 10.1016/S0031-3203(96)00160-4 [DOI] [Google Scholar]
- Wu LQ, Niu YQ, Yang J, Wang SR (2005) Tectal neurons signal impending collision of looming objects in the pigeon. Eur J Neurosci 22:2325–2331. 10.1111/j.1460-9568.2005.04397.x [DOI] [PubMed] [Google Scholar]
- Wurtz RH (2009) Superior colliculus. In: Encyclopedia of Neuroscience (Squire L, ed), pp 627–634. Oxford: Academic Press. [Google Scholar]
- Wurtz RH, Sommer MA, Paré M, Ferraina S (2001) Signal transformations from cerebral cortex to superior colliculus for the generation of saccades. Vision Res 41:3399–3412. 10.1016/S0042-6989(01)00066-9 [DOI] [PubMed] [Google Scholar]
- Xue M, Atallah BV, Scanziani M (2014) Equalizing excitation-inhibition ratios across visual cortical neurons. Nature 511:596–600. 10.1038/nature13321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatorre R, Belin P, Penhune VB (2002) Structure and function of auditory cortex: music and speech. Trends Cogn Sci 6:37–46. 10.1016/S1364-6613(00)01816-7 [DOI] [PubMed] [Google Scholar]
- Zénon A, Krauzlis RJ (2012) Attention deficits without cortical neuronal deficits. Nature 489:434–437. 10.1038/nature11497 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao X, Liu M, Cang J (2014) Visual cortex modulates the magnitude but not the selectivity of looming-evoked responses in the superior colliculus of awake mice. Neuron 84:202–213. 10.1016/j.neuron.2014.08.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zipser D, Andersen RA (1988) A back-propagation programmed network that simulates response properties of a subset of posterior parietal neurons. Nature 331:679–684. 10.1038/331679a0 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data and code for reproducing the results in this paper are available in the following repository: https://github.com/yashmrsawant/ChangeDetection_stRNN.