Fig. 3. Size scaling of the simulated crossover temperature for the different 2D lattices.

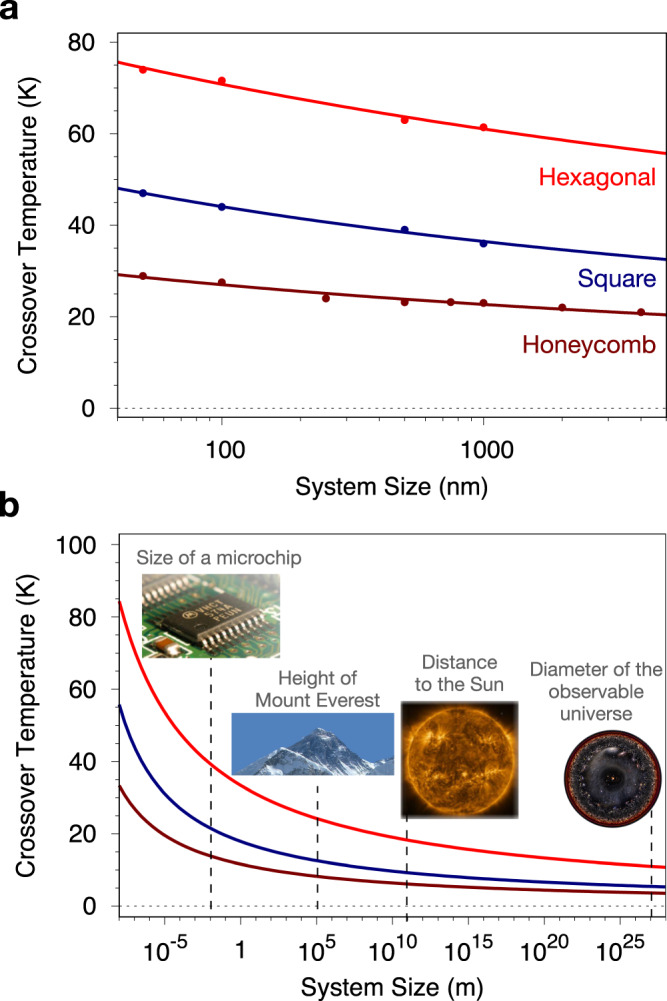
a Variation of the crossover temperature T_x with system size for different symmetries (Hexagonal, Square, Honeycomb) on a log-scale. The curves are a fit using $T_x=A/\log \left(L/B\right)$, where A and B are fitting constants and L is the system size. A and B are 327.28 K and 0.000542 nm, 484.96 K and 0.00166 nm and 1018.50 K and 5.7 × 10⁻⁵ nm for honeycomb, square and hexagonal lattices, respectively. b Extrapolation of the exponential fits in a to larger sizes on all studied symmetries. The crossover temperature remains finite (>4 K) for systems as large as ~ 10²⁵ m indicating no dependence of the magnetic anisotropy for stabilisation of magnetic ordering. Insets provide a comparison with physical distances observed in different systems. Figures in b are adapted with permission under a Creative Commons CC BY license from Wiki Commons. Microchip: Integrated circuit on a microchip by Jon Sullivan, 2006, at Public Domain from Wiki Commons. Sun: inset is from ESA & NASA/Solar Orbiter/EUI team, 2022 at Public Domain from Wiki Commons. Data processing by E. Kraaikamp. Everest: Wikivoyage banner for Mount Everest or Nepal by Fabien1309. This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. Universe: The Observable Universe by Pablo Carlos Budassi from Wikipedia under Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0) in Public Domain.