Abstract
Background and Objectives
Prediction of antimicrobial target-site pharmacokinetics is of relevance to optimize treatment with antimicrobial agents. A physiologically based pharmacokinetic (PBPK) model framework was developed for prediction of pulmonary pharmacokinetics, including key pulmonary infection sites (i.e. the alveolar macrophages and the epithelial lining fluid).
Methods
The modelling framework incorporated three lung PBPK models: a general passive permeability-limited model, a drug-specific permeability-limited model and a quantitative structure–property relationship (QSPR)-informed perfusion-limited model. We applied the modelling framework to three fluoroquinolone antibiotics. Incorporation of experimental drug-specific permeability data was found essential for accurate prediction.
Results
In the absence of drug-specific transport data, our QSPR-based model has generic applicability. Furthermore, we evaluated the impact of drug properties and pathophysiologically related changes on pulmonary pharmacokinetics. Pulmonary pharmacokinetics were highly affected by physiological changes, causing a shift in the main route of diffusion (i.e. paracellular or transcellular). Finally, we show that lysosomal trapping can cause an overestimation of cytosolic concentrations for basic compounds when measuring drug concentrations in cell homogenate.
Conclusion
The developed lung PBPK model framework constitutes a promising tool for characterization of pulmonary exposure of systemically administrated antimicrobials.
Supplementary Information
The online version contains supplementary material available at 10.1007/s40262-022-01186-3.
Key Points
| A lung physiologically based modelling framework was developed to predict antimicrobial concentrations in lung epithelial lining fluid and alveolar macrophages. |
| Integration of a machine learning-based quantitative structure prediction model allows generic prediction of lung pharmacokinetics. |
| We demonstrate the importance of incorporating drug-specific permeability and the role of lysosomal trapping for prediction of lung target site concentrations. |
Introduction
Consideration of antimicrobial target site concentration at the site of infection is crucial to derive treatment strategies with optimal efficacy and minimize the risk for antimicrobial resistance [1]. For respiratory tract infections (RTIs), key target sites include the epithelial lining fluid (ELF) and alveolar macrophages (AMs) [2]. Drug concentrations in ELF and AM may be significantly different compared with the plasma [3].
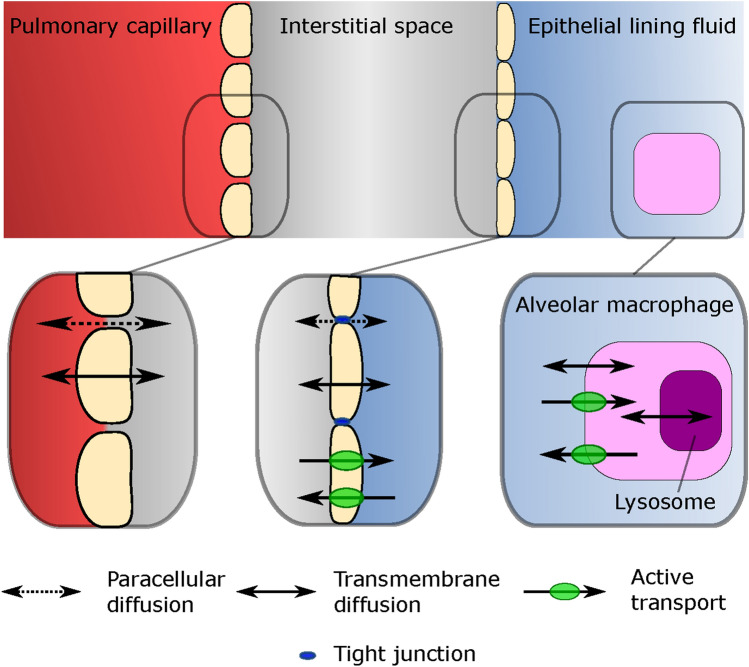
Systemically administered drugs pass through the pulmonary capillary wall, into the interstitial space, and cross the alveolar epithelium (Fig. 1). The alveolar epithelium acts as a semi-permeable barrier with tight junctions restricting paracellular diffusion [4] and active drug transporters [5]. For intracellular uptake of antibiotics in AMs, passage through the cell membrane by means of passive diffusion or active transport is needed. Intercellular pathogens in AMs localize in the cytosol, that is, outside of the lysosomes. The low pH of lysosomes compared with the cytosol can alter the charge of molecules entering this compartment, causing lysosomal trapping [6], thereby decreasing the target site concentrations in AM cytosol. Together, these processes lead to target-site concentrations in the ELF and AM that may deviate from plasma.
Fig. 1.
Overview of physiological compartments in the lung, their associated barriers and the different modes of transport available over the specific barriers
Pathophysiological changes during infection, or due to comorbidities, may lead to increased permeability over the alveolar epithelium [7], increased ELF volume [8], AM recruitment [9] and acidification of the ELF [10] and/or the interstitial fluid. Consequently, these pathophysiological changes may further alter the (expected) target-site concentrations of antibiotics. However, pulmonary pharmacokinetics (PK) is currently under-studied in patients [2], typically relying on clinical studies in healthy volunteers [2].
The quantification of ELF and AM drug concentrations is typically achieved by bronchoalveolar lavage (BAL) sampling [2]. Commonly, only a single BAL is performed per subject and the method is associated with high measurement variability [11]. In silico modelling approaches predicting pulmonary drug exposure can thus provide valuable complementary insights. Here, quantitative structure–property relationship (QSPR)-based approaches are of interest to predict ELF-to-plasma ratio (EPR) based on chemical structural features alone [12, 13]. However, QSPR models lack the ability to explore the full ELF PK and do not allow the evaluation of pathophysiological effects on PK. In this context, physiologically based PK (PBPK) models can be of value as they allow for the prediction of drug concentration in physiological compartments based on physiological and drug-specific parameters.
Several lung PBPK models have been previously developed [14–16]. These models constitute important tools to predict ELF PK. However, they lack the representation of one of the key microbial infection sites, the AMs. In addition, the aforementioned PBPK models rely on in vitro or in vivo data of apparent permeability to describe drug transport over the alveolar epithelium. This limits previous models’ applicability in cases where permeability data are lacking.
Here, we aimed to address these limitations by developing a novel lung PBPK model framework to predict PK of small molecule drugs at key target sites for RTIs (i.e. ELF and AMs), accounting for spatial heterogeneity in lung physiology. Specifically, we developed and evaluated three complementary lung PBPK models for systemic antimicrobials, (1) a general passive permeability-limited model, (2) a drug-specific permeability-limited model and (3) a QSPR-informed perfusion-limited model. We applied the different models to a fluoroquinolone data set. We then used the passive transport model to identify the main drug properties affecting pulmonary PK and evaluate the effect of pathophysiologically related changes.
Methods
The PBPK modelling and simulation framework relied on the integration of modular components that include the PBPK base model, and three alternative model implementations of the lung. The different lung PBPK models included different approaches of describing pulmonary drug transport: (1) a general passive permeability-limited model, (2) a drug-specific permeability-limited model and (3) a QSPR-informed perfusion-limited model.
Physiologically Based Pharmacokinetic (PBPK) Model Structure
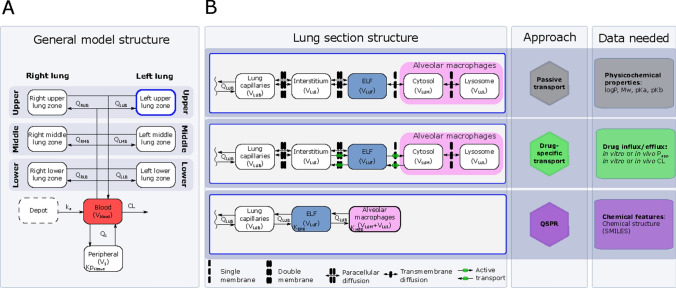
A minimal-PBPK model was developed that includes a physiological blood reservoir compartment, a physiological peripheral compartment and a detailed physiological lung section. The base structure of the developed model is shown in Fig. 2A. The lung section represents the lower respiratory tract and was divided into six different zones to account for the spatial differences of the volume, surface area and blood between the right and left lungs, as well as the upper, mid and lower part of each lung. Each of the different lung zones were further divided into serially linked physiological compartments (Fig. 2B), with the aim to describe ELF and AM concentrations. Blood–lung drug transport was implemented using the three alternative models.
Fig. 2.
PBPK model structure and associated approaches and data requirements. A General model structure of the minimal PBPK model including the lung section with the six different lung zones. The full cardiac output (Qc) is heterogeneously divided over the different lung zones (z) to account for spatial difference in pulmonary blood flow (QZB). The blood clearance (CL), tissue-to-blood partitioning for the peripheral compartment (Kptissue) and apparent absorption rate (ka) are implemented as empirical parameters while the other included parameters are physiologically derived. B Overview of three variations of the lung sub-model using different approaches to describe lung drug disposition and what data each approach required. ELF epithelial lining fluid, PBPK physiologically based pharmacokinetic, QSPR quantitative structure-property relationship, V volume, LXX left lung, RXX right lung, XUX upper lung zone, XMX middle lung zone, XLX lower lung zone, XXB blood compartment, XXI interstitial compartment, XXF ELF compartment, XXM cytosol compartment, XXL lysosome compartment, KEPR ELF-plasma partitioning, KMER alveolar macrophage -ELF partitioning
The permeability-limited models included five compartments for each of the six lung zones, representing the lung capillaries, the interstitial space, the ELF, the AM cytosol and the AM lysosomes. The perfusion-limited model included three compartments for each lung zone, representing the lung capillaries, the ELF and the AMs, respectively. For all three models, only the free unbound drug was assumed to distribute from the pulmonary capillaries into the subsequent compartment. Protein binding was assumed negligible for all pulmonary non-blood compartments.
Blood Drug Disposition Model
The drug disposition in the blood reservoir and peripheral compartment after intravenous administration was described by the following ordinary differential equations (Eqs. 1, 2):
| 1 |
| 2 |
where Ablood, Aperipheral and AZB, and Vblood, Vperipheral and VZB represents the amount of drug in the different compartments and their related volumes, respectively, CL the blood clearance, Kptissue the tissue-to-blood partitioning for the peripheral compartment, Qc the cardiac output and QZB zone-specific blood flow. Here, ZB is the pulmonary capillary compartment (B) of lung zone Z, which includes right upper, middle and lower zone (RUB, RMB and RLB, respectively), and their left side counterparts (LUB, LMB and LLB).
Oral drug administration was implemented using a depot compartment with a first-order apparent absorption rate (ka).
Physiological Parameters
The model framework was developed using a combination of empirically estimated plasma PK parameters including CL, Kptissue and ka, and physiological system-specific parameters derived from literature (Table 1). Briefly, the total body volume was derived from the bodyweight, assuming a density of 1 L/kg. The total volume was made up of the volume of the blood reservoir (7.71% [17]), the volume of the lower respiratory tract (0.63% [14, 17]) and the residual volume associated with the peripheral compartment (91.7%). The volume related to the AMs (~ 1.2 mL) was derived from the concentration of AMs in the ELF [11], the ELF volume [14] and the volume per AM [18]. The total AM volume was divided over the cytosol and the lysosomes, which accounts for 87% and 9.3% of the total AM volume, respectively [6]. The AMs and lysosomes were assumed to be spherical and each AM contained one lysosome. The spatial difference in volumes, surface areas and perfusion within the lower respiratory tract were implemented by relating factions of these to the left and right side [19], and further splitting those into upper, middle and lower lung zones [20].
Table 1.
Physiological system-specific parameters used in the developed physiologically based pharmacokinetic model
| Parameter | Description | Value | Unit | Type | References |
|---|---|---|---|---|---|
| Qc | Cardiac output | 390 | L/h | Model assumption | [17] |
| FQ,Upper | Fraction perfusing the upper lung zone | 0.116 | Experimental | [20] | |
| FQ,Middle | Fraction perfusing the middle lung zone | 0.297 | Experimental | [20] | |
| FQ,Lower | Fraction perfusing the lower lung zone | 0.587 | Experimental | [20] | |
| FQ,Left | Fraction perfusing the left lung | 0.46 | Experimental | [19] | |
| FQ,Right | Fraction perfusing the right lung | 0.54 | Experimental | [19] | |
| DBlood | Volume blood per kg bodyweight | 0.0771 | L/kg | Model assumption | [17] |
| DLung | Volume lung per kg bodyweight | 0.0076 | L/kg | Model assumption | [17] |
| VPBR | Total volume of blood in lung | 89 × 10−3 | L | Model assumption | [14] |
| Finterstitium | Fraction of lung volume equal to the interstitium volume | 0.2 | [41] | ||
| VELF | Total ELF volume | 25 | mL | mean value from several studies | [14] |
| NAM,F | Number of macrophages | 1.99 × 1013 | cells/L | Upper range of clinical study | [11] |
| VAM | Volume per macrophage | 2.42 × 10−12 | L | [18] | |
| VLys | volume per alveolar lysosome | 0.0166 × 10−15 | L | Experimental | [42] |
| FLRT | Fraction of lung representing the lower respiratory tract | 0.833 | Model assumption | [14] | |
| FV,Upper | Split volume fraction | 0.25 | Experimental | [43] | |
| FV,Middle | Split volume fraction | 0.36 | Experimental | [43] | |
| FV,Lower | Split volume fraction | 0.39 | Experimental | [43] | |
| FV,Right | Split volume based on the lung side | 0.534 | Experimental | [43] | |
| FV,Left | Split volume based on the lung side | 0.466 | Experimental | [43] | |
| FV,Cyto | Cytosol fraction of total AM volume | 0.87 | Mean experimental values | [6, 6] | |
| FV,L | Lysosome fraction of total AM volume | 0.093 | Mean experimental values | [6, 6] | |
| ASA | Alveolar epithelial surface area | 130 × 102 | dm2 | Combined studies | [45] |
| BSA | Luminal capillary surface area | 117 × 102 | dm2 | Combined studies | [45] |
| AMSA | Surface area per macrophage | 8.72× 10−8 | dm2 | Derived from AM volume | |
| LSA | Surface area per lysosome | 14.6 × 10−11 | dm2 | Experimental | [42] |
| ThB | Thickness of blood endothelial | 0.46 × 10−5 | dm | Combined studies | [45] |
| ThA | Thickness of pneumocytes | 0.3 × 10−5 | dm | Combined studies | [45] |
| ProAM | Protein per macrophage | 107 × 10−9 | mg/cell | Experimental | [46] |
| pHELF | pH in ELF | 6.6 | Mean of combined studies | [10] | |
| pHinterstitium | pH in interstitial fluid | 7.4 | Mean of combined studies | [10] | |
| pHcytosol | pH in AM cytosol | 7.2 | [6, 6] | ||
| pHlysosme | pH in AM lysosomes | 4.75 | [6, 6] | ||
| Prs | Pore size of small pores in epithelial tight junctions | 0.32 × 10−8 | dm | Experimental | [25] |
| Prl | Pore size of large pores in epithelial tight junctions | 11.56 × 10−8 | dm | Experimental | [25] |
| PAs | Fraction of total alveolar area of small pores | 3.03 × 10−3 | Experimental | [25] | |
| PAl | Fraction of total alveolar area of large pores | 7.90 × 10−7 | Experimental | [25] |
AM alveolar macrophages, ELF epithelial lining fluid
The General Passive Permeability-Limited Model
Passive transport in the lung includes paracellular and transmembrane diffusion (Fig. 1). Transmembrane diffusion refers to the passive diffusion occurring through the phospholipid bilayers in the membrane of the endothelial cell of the pulmonary capillaries, the alveolar epithelium and the AMs and their lysosomes. The transmembrane transport was implemented according to Eq. (3) [21, 22], where only the neutral fraction (NF) was assumed to be available for transmembrane transport.
| 3 |
where PTM is the transmembrane permeability (cm/s) over a single membrane and logP the n-octanol lipophilicity index. For cell barriers, the transcellular permeability was obtained by dividing PTM by two, thus accounting for the double membrane passage needed to pass through the cell.
The compartment-specific NF of the drug was calculated using an adapted Henderson–Hasselbalch equation (Eq. 4) [23], relating the NF of the strongest acidic group (NFacidic) and the strongest basic group (NFbasic) of the drug according to Eqs. (5) and (6), respectively.
| 4 |
| 5 |
| 6 |
The surface area available for transmembrane transport over the luminal side of the capillaries was assumed to be 99.8% of the total surface area [22], while the remaining area was assumed to be paracellular space. The surface area of the alveolar epithelium available for transmembrane transport was assumed equal to the full alveolar surface area minus the total area of the aqueous pores in the tight junctions. The full surface area of the AMs and the lysosome were available for transmembrane transport.
The alveolar capillary wall is a highly permeable structure [24], and therefore the full paracellular space was assumed to be available for transport. Paracellular transport over the alveolar epithelium is restricted by tight junctions [24, 25], and was assumed to only take place through aqueous pores present in tight junctions. The pore population consisted of two subpopulations, one small (rs 0.32 nm radius) and one large (rl 11.52 nm radius), making up 0.303% and 0.00079% of the total alveolar surface area, respectively [25]. Passage through the pores was assumed possible for molecules with radius r smaller than the pore radius (rs or rl). Molecules that met the size criteria diffused according to Eq. (7) [22, 26] without any charge restriction.
| 7 |
where Daq is the aqueous diffusivity coefficient (cm2/s) and Mw is the molecular weight (g/mol). The molecular radius r was assumed to be constant and calculated according to the Stoke–Einstein equation (Eq. 8) [25, 27].
| 8 |
where k is the Boltzmann constant (1.38*10−23 J/K), T is the absolute body temperature (309.95 K) and η is the viscosity of water at 309.95 K (0.69 mPa × s) [28].
The Drug-Specific Permeability-Limited Model
We included the option to incorporate drug-specific influx and efflux over the alveolar epithelium and the macrophage membrane. The drug-specific transport was informed by literature data from in vitro permeability assays using human-cultivated alveolar epithelial cells (Calu-3 cells) or rat AMs. The in vitro-derived permeability was assumed to represent both active and passive transport processes.
The Perfusion-Limited QSPR-Informed Model
To allow for the structure-based predictions of drug penetration into the ELF and the AM, we first fitted two QSPR-based elastic net regression models predicting the log steady-state concentration ratio for ELF–plasma ratio (EPR) and AM–ELF ratio (MER) according to our previously described method [12]. Briefly, clinical data for 40 anti-infective agents on systemic and pulmonary exposure (ELF and AMs) [12] were extracted from literature and pre-processed as previously described [12]. The dataset was divided into training (n = 32) and test (n = 8) datasets for the development and validation of the QSPR models, respectively. The training set included compounds covering wide ranges for different molecular descriptors, for example, logP: − 5.86–4.26, Mw: 123.11–1755.64, 0–3 and 0–5 functional acidic and basic groups, respectively. A full overview of molecular descriptors of the training and test datasets can be found in Supplementary Table S1 and S2, respectively (see electronic supplementary material [ESM]). The test dataset included the three fluoroquinolones used in our model application examples. Elastic net tuning was optimized by minimizing the root mean-squared error (RMSE) and leave-one-out cross-validation.
As the QSAR models are based on chemical descriptors, no within-drug variability (WDV) associated with other factors could be accounted for. Therefore, we derived a theoretical upper limit for the R2 () in accordance with a previously described approach [12], where is defined as
| 9 |
where Cobs,i,a is the ith observation of the ath drug and Cobs,mean,a is the mean observation for the ath drug. The WDV corrected R2 () was defined as
| 10 |
where Cpred,a is the prediction of the ath drug and the the proportion of between-drug variability that can be predicted by the model. The QSPR-derived ratios were incorporated into the perfusion-limited model. The ratios were included as partitioning coefficients where the EPR and MER represented the partitioning of free drug between the plasma and ELF and the ELF and AMs, respectively.
Modelling Framework Applications
Application to Fluoroquinolone Antibiotics
We applied the framework to three fluoroquinolone antibiotics. We first digitized data from previously conducted studies characterizing the steady-state lung PK of ciprofloxacin [29], grepafloxacin [30] and levofloxacin [31] (Table S3, see ESM). The study-specific mean body weight was used to calculate physiological parameters. We empirically derived the tissue-partitioning coefficient (Kptissue), the (apparent) plasma clearance (CL) and apparent absorption constant (ka), when applicable, from the naïvely pooled observed plasma concentration data using nonlinear regression.
We applied and compared the three different lung models, using the mean concentrations of the different lung zones. Prediction performance was evaluated by calculating RMSE.
Exploring the Effect of Drug Properties on Pulmonary Drug Exposure
Using the passive model, we simulated treatments of different hypothetical antimicrobials to better understand how biological and drug-specific properties (Mw, logP, pka, pkb) affect pulmonary PK. Specifically, we defined a comparator drug for each molecule, which had a CL of 10 L/h, Kptissue of 1, logP of zero and Mw of 500 g/mol. To allow for the evaluation of the impact of certain drug-specific parameters on pulmonary PK, we varied Kptissue, logP and Mw for three different drug molecules: one acid (pka = 3, pkb = − inf), one base (pka = − inf, pkb = 9) and one neutral (pka = inf, pkb = − inf).
For each tested drug, the steady state maximal concentration (Cmax) and 24-h area under the curve (AUC) were calculated. These exposure metrics were used to calculate the log2 ratio (L2R) of the metric of the specific drug x and its comparator according to Eq. (11), where a value of 1 represents a 2-fold increase and −1 a 2-fold decrease.
| 11 |
where metric is either steady-state AUC or Cmax.
Quantifying the Effect of Pathophysiology on Pulmonary Drug Exposure
Pathophysiological changes can alter antimicrobial PK. To understand how such changes can influence pulmonary PK, we varied selected parameters known to be affected by infections. Using the passive model, we simulated treatments with a set of different hypothetical antimicrobials while increasing the ELF volume, the number of AMs or the size of the small pores in the alveolar epithelium, or decreasing the pH in the ELF or the interstitial fluid. To evaluate the effect of pathophysiology, we defined a base scenario for each different molecule, where the physiological parameters represent that of a healthy individual. The impact of pathophysiological changes was assessed for each drug by calculating the L2R of the metric (AUC or Cmax) of the disease scenario and the base scenario, analogous to Eq. (9).
Software and Model Code
All PK analyses were performed in R (v. 4.2.1), using the packages nlmixr (version 2.0.7) and RxODE (version 1.1.6). All code related to the PBPK framework is available as supplementary information (see ESM). The elastic net QSAR-models were developed using the R packages caret (version 6.0-88), elasticnet (version 1.3) and rcdk (version 3.5.0).
Results
The Developed QSPR-Based Models Predict Pulmonary Drug Penetration
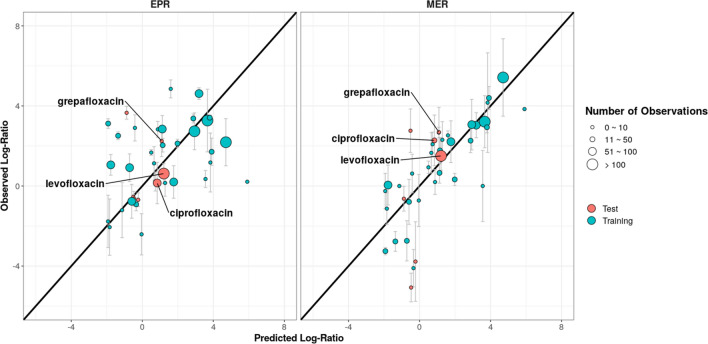
The predictive performance of the fitted QSPR-based models is shown in Fig. 3. The EPR model was used to predict the log steady-state ELF-to-plasma ratio (log-EPR) for the training (RMSE = 1.17, = 0.92, = 0.84) and for the test set (RMSE = 1.14, = 0.76, = 0.56). The log-EPR was 1.69, 1.53 and 1.47, for grepafloxacin, ciprofloxacin and levofloxacin, respectively. Similarly, the MER model was used to predict the log-AM-to-ELF ratio (log-MER) the training (RMSE = 1.57, = 0.94, = 0.94) and the test set (RMSE = 2.03, = 0.70, = 0.83). The predicted log-MER for grepafloxacin, ciprofloxacin and levofloxacin were 1.09, 0.84 and 1.21, respectively. The result from the optimization of tuning parameters can be seen in Fig. S1 (see ESM).
Fig. 3.
Predicted versus observed log epithelial lining fluid–plasma ratio (EPR) and alveolar macrophage–epithelial lining fluid ratio (MER). They each include 130 structural features and the s and λ were 0.20 and 0.10 for the EPR model and 0.25 and 0.25 for the MER model, respectively. The error bars represent the reported range of the within-study mean observed penetration log ratios
Prediction of Fluoroquinolone Lung Pharmacokinetics
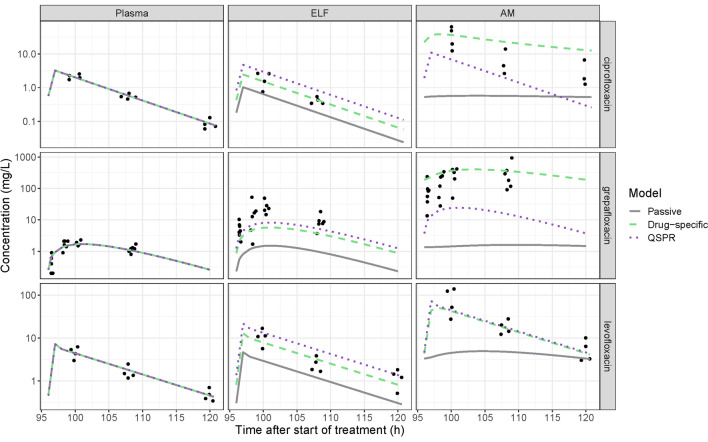
Plasma concentration data could be described well for all tested fluoroquinolone antibiotics (Fig. 4). Fitted parameters can be found in Supplementary Table S4 (see ESM). Out of the three different lung models, the passive model performed the worst for all three antibiotics (Fig. 4 and Fig. S2, see ESM), with RMSE ranging between 0.98 to 2.39 and 1.85 to 4.57 for the ELF and AMs, respectively. The passive model predicted a very slow equilibration between the ELF and AMs, leading to a systematic under-prediction of the AM concentrations. Overall, the approach using in vitro-informed active transport outperformed the QSPR approach, except for the ELF prediction of grepafloxacin (RMSE 1.18 and 0.92 for active and QSPR approaches, respectively) and AM prediction of levofloxacin (RMSE 0.60 and 0.58 for active and QSPR approaches, respectively). Regardless of which approach used, there was no heterogeneity in the drug distribution into the different lung zones (data not shown).
Fig. 4.
Steady-state pharmacokinetic (PK) profiles of repeated dosing of ciprofloxacin, grepafloxacin and levofloxacin in plasma, epithelial lining fluid (ELF) and alveolar macrophages (AMs). Observations are shown as dots and model predictions as lines, where the predicted concentration in the pulmonary compartments are the mean of the six lung zones. Three different models were used to predict pulmonary PK; a general passive permeability-limited model (grey solid lines), a drug-specific permeability-limited model (green dashed lines) and a quantitative structure–property relationship (QSPR)-informed perfusion-limited model (purple dotted lines)
Drug-Specific Effects
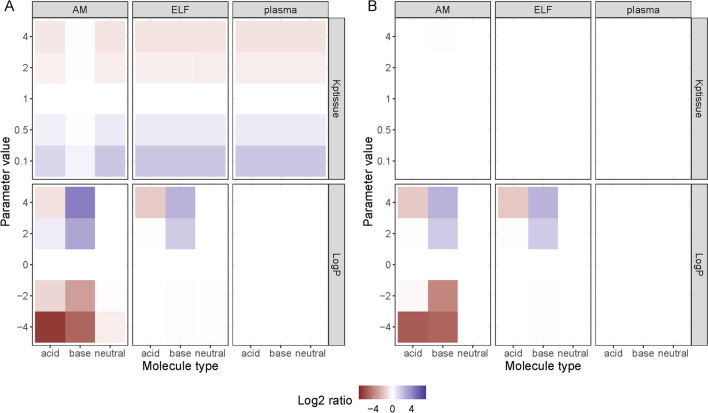
The investigation of how different drug-specific and empirical PK parameters influence the pulmonary PK revealed how molecules with different charges (i.e. acid, base, or neutral) were affected differently (Fig. 5). Exposure at the AM compartment was more affected by logP when the drug was an acid or a base, as compared to a neutral compound. The Kptissue parameter affects drug distribution, and as such it had no effect on AUC, while the Cmax increased or decreased as a function of Kptissue for all drugs and compartments except at the AM compartment for the basic compounds, which remained unaffected. This could be related to the very slow equilibration between the ELF and the AMs for the basic compounds, which leaves changes in the ELF concentration to have less effect on the AM concentration (Fig. S3, see ESM). A large impact of decreasing logP values on Cmax and AUC in AM and ELF compartments was seen. The Mw had no impact on the L2R for any of the drug types (data not shown). Mw below 80 g/mol was required to pass through the population of small pores (i.e. r < 0.32 nm) while the lowest Mw simulated was 200 g/mol (r = 0.49 nm). Similarly, all simulated molecules had free passage through the population of large pores (rl = 11.56 nm). However, the total available surface area was considerably smaller for the large pores compared with the small (0.00079% and 0.303% of the total alveolar surface area, respectively).
Fig. 5.
Impact of drug-specific parameters on A steady-state maximum concentration and B 24-h area under the curve (AUC) for plasma, epithelial lining fluid (ELF) and alveolar macrophages (AMs). The drug-specific parameter altered included tissue partitioning coefficient (Kptissue), the n-octanol-water lipophilicity index (logP) and plasma clearance (CL) and molecular weight (data not shown). The drugs with median parameter values were used as comparator drugs and the colour gradient indicate the log2 change in AUC (A) or Cmax(B) relative to the comparator
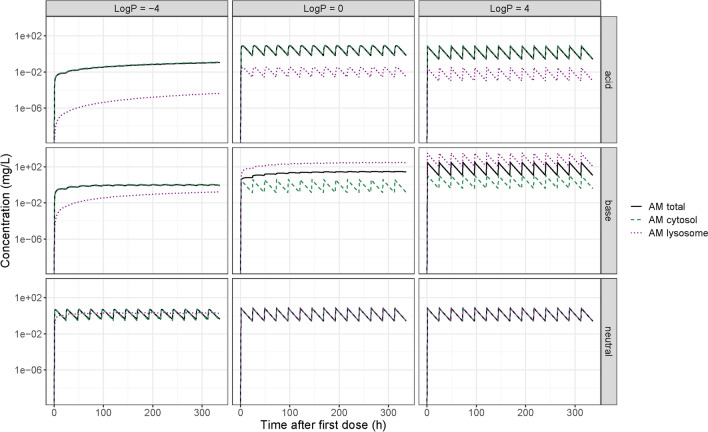
We characterized the impact of molecule type (acid, base, or neutral) and logP on predicted time–concentration profiles in plasma, ELF and AM compartments (Fig. 5). Generally, the acidic and neutral compounds showed high agreement between the total AM drug concentration and the AM cytosol concentration. In these cases, lysosomal trapping has minimal impact on the drug availability at the site of infection (Fig. 6). However, for basic compounds, large differences could be seen between the total AM and the cytosolic concentration. Therefore, lysosomal trapping can play a major role for the intercellular PK and if not considered, may lead to the overestimation of antimicrobial concentration at the site of action (cytosol).
Fig. 6.
Pharmacokinetics of the alveolar macrophages (AM), and their intercellular compartments for nine hypothetical drugs with different properties
Pathophysiological Effects
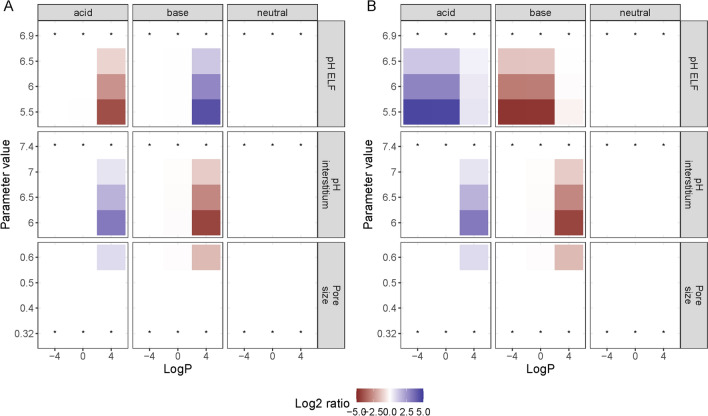
Following the sensitivity analysis for drug-specific parameters, we selected acidic, basic and neutral antimicrobials with a range of logP values (−4, 0 and 4) and a relatively low Mw (300 g/mol, r = 0.57 nm). Plasma concentrations remained unaffected by the pathophysiological changes simulated (Fig. S4, see ESM), while the pH of the ELF and interstitium, as well as the size of the pores in the alveolar epithelium, had an effect on the ELF and AM AUC (Fig. 7), and a corresponding effect on Cmax (Fig. S4, see ESM). The neutral molecules were unaffected by the changes in the system-specific parameters, while the acidic and the basic compounds were affected in opposite ways. Drugs of different lipophilicity were affected differently by the pathophysiological changes. Most changes only affect lipophilic drugs (logP = 4). Interestingly, acidification of the ELF affected the more hydrophilic non-neutral compounds (logP 0 or −4). This could be explained by the shift in NF available to pass over the macrophage membrane. As passage through pores is only available for molecules with a smaller radius than the pores themselves, a large enough increase in the radius of the small pores can make this pore population available and subsequently increase the surface area available for paracellular diffusion. This mainly influences basic and acidic lipophilic molecules, as they diffuse largely via transcellular diffusion when neutral, but can get trapped when protonated or deprotonated due to pH differences between compartments. Important here is that only the neutral fraction can diffuse over the membrane, while the paracellular route is available without any charge restrictions. When increasing the radius of the small pores, and subsequently the area available for paracellular transport, the ratio between the transcellular and paracellular transport will shift (Fig. S5, see ESM) and the impact of the trapping decreases. Due to the absence of charge restrictions related to the paracellular route, the pH differences between the compartments has less impact. This results in a decreased concentration difference between the compartments.
Fig. 7.
Impact of pathophysiological related changes to system-specific parameters on steady 24-h area under the curve (AUC) for epithelial lining fluid (A) and alveolar macrophages (B) for different drugs. The parameter values of the base scenario are indicated with* And the colour gradient indicate the log2 change in AUC relative to the base scenario
Discussion
We developed a novel lung PBPK modelling and simulation framework and applied this to study fluoroquinolone PK and investigate the impact of drug-specific properties and disease-related changes on pulmonary PK of hypothetical antimicrobials.
By comparing the different model-based predictions of pulmonary PK, we could identify the importance of considering drug-specific transport, including active processes. Thus, informing the model with permeability data derived from cell-based in vitro assays proved to be the best performing approach.
We informed the transport over the alveolar epithelium with permeability data obtained from Calu-3 cell assays. However, such assays are not commonly performed and therefore relevant data are often lacking. In contrast, assays quantifying intestinal permeability are routinely performed for orally administered drug, primarily using Caco-2 cells. Models predicting Calu-3 permeability based on Caco-2 permeability have been developed [14]. Such models could be incorporated into our framework to allow for simulation of pulmonary PK considering drug-specific transport in the absence of Calu-3 data. However, there are no equivalent translational models for macrophage permeability and currently such data are not commonly available. Furthermore, in a comparison between the more well established Calu-3 cell assay and current state-of-the-art 3D cell cultures that recapitulates the structure and composition of human airways, large differences were found in the transporter expression [32]. Informing the developed modelling framework with data derived using more advanced in vitro models with more relevant transporter expression could aid in further improving the model predictions.
The QSPR-based approach, which accounts for active transport processes, was clearly outperforming the approach where only passive diffusion was included (Fig. 4). The QSPR-based approach could therefore constitute a relevant alternative to the in vitro-informed active transport in situations where such data are not available. Due to the modularity of the developed model, the QSPR-based and in vitro-informed approaches could easily be combined. The QSPR approach could be implemented to compensate for missing permeability data for either the alveolar epithelium or the macrophage membrane, depending on data availability. Of note, although the penetration ratios of the studied fluoroquinolones were well predicted, other drugs were less well predicted, especially for the MER. Some of these drugs were associated with large reported MER ranges, which the devolved QSAR models cannot account for.
The modelling framework was used to understand the impact of drug-specific parameters on pulmonary PK. To this end, we used the passive PBPK model. Although this model performed the worst in the model application example, it serves as a useful foundation to pull apart the impact of specific factors on pulmonary PK. We found that lipophilicity was a highly influential drug property in combination with molecular type (i.e. acidic, neutral, basic). Only pathophysiological changes that altered the proportion between transcellular and paracellular transport had an effect on ELF drug exposure, which subsequently altered the AM exposure. The AM exposure was further affected by shifts in the ELF neutral fraction. For acidic compounds, this fraction was increased with increased acidity, and subsequently more drug was available to pass over the AM membrane. As the pH remained the same within the AMs, the fraction available to diffuse back to the ELF was unchanged, resulting in an increase of AM drug concentration. The reverse occurred for the basic compounds.
Although we show that lipophilic drugs tend to exhibit a high grade of lung penetration, there is a high likelihood that such compounds will have poor systemic PK properties and may not reach the lung before they are cleared. This suggests that targeting lung exposure alone may not be a fruitful approach for systemically administered compounds. To overcome this issue, we see the value of a multifactorial QSPR/PBPK approach in which multiple drug properties are optimized simultaneously in respect to both systemic and pulmonary PK.
We demonstrate that lysosomal trapping can have a large impact on pulmonary PK. To highlight the relevance of this finding, we can offer a recent example. Back in 2020, when the COVID-19 pandemic was starting, hydroxychloroquine (HCQ) was hypothesized as a potential treatment for COVID-19 [33]. HCQ showed in vitro efficacy and promising lung tissue distribution, suggesting that HCQ should inhibit coronavirus at clinically feasible doses [33]. However, HCQ was found ineffective as a COVID treatment [34, 35]. The lung-plasma partitioning ratio of HCQ is very high, but this high partitioning was a result of lysosomal trapping [36–38]. Moreover, in vitro efficacy had been related to cell culture media concentrations [33], which corresponds to extracellular fluid. The extracellular fluid concentrations in lung tissue were much lower than overall lung tissue, and thus no effective and safe HCQ dosing regimens could be identified. As such, we contend that lysosomal trapping should be explicitly included in lung PK predictions, while at the same time keeping in mind the site of action of the drug. The developed lung PBPK model constitutes a highly customizable modelling framework and the modular structure of the framework allows the adaptation to data availability. A main practical advantage of the framework is that it was developed in the open source software R [39]. This makes it accessible and flexible, allowing for adjustments of the current model but also the incorporation of model extensions. Therefore, we see this framework as a relevant complementary addition to currently available lung PBPK models implemented in other software packages.
We developed the model balancing complexity and pragmatism to find a simple structure that included important physiological features related to systemic administration of antimicrobials and can capture the pulmonary PK. A key element in our model is the explicit inclusion of two-compartmental alveolar macrophages, which describe cytosolic PK while considering lysosomal trapping. Such implementation is not seen in the previously mentioned PBPK models [14–16]. Additionally, by separating permeability into passive paracellular, passive transcellular and active transport we could investigate the importance of these routes and how that can change in different pathophysiological conditions.
The model developed by Hartung and Borghardt [16] is intended for orally inhaled drugs, which adds several levels of complexity through consideration of airway generation and mucociliary clearance. As our framework is intended for systemically used drugs, we deemed that a simplified structure could sufficiently describe the pulmonary PK after such administration. However, we did not differentiate deep lung or consider the dynamical processes in the ELF. Therefore, the current model structure is unsuitable for inhaled drugs. Eriksson et al. [15] present a simpler model compared with the Hartung model, where the lung is divided into an alveolar and a bronchial sub-compartment. In line with their discussion on airway structure, we consider it is not clear if added complexity would be beneficial for the prediction performance of the model, especially given the uncertainty in the spatial origin of the data used. Here, specialized sampling techniques like microdialysis [40] could play a role in increasing the granularity of data.
The data used to validate the model were digitized from clinical BAL studies, which is associated with minor inaccuracies due to the digitization procedure. However, BAL studies are known to have high variability. In this context, we expect such digitization inaccuracies will have negligible impact on our analysis and predictions. Of note, there were several values below the limit of quantitation (LOQ) for the ELF concentrations of ciprofloxacin. As these concentrations were simulated by the model but not used for the estimation, these values will not lead to bias in the parameter estimates. In line with the observed data, in our simulations any values below the lower LOQ were excluded. A further perspective to build more confidence in the model predictions would be to validate the model with lung PK data of antimicrobials with different physicochemical properties. However, this is currently hindered by the availability of such data.
Conclusion
The developed PBPK model framework can support improved characterization of pulmonary exposure of systemically administrated antimicrobials to guide treatment optimization for RTIs.
Supplementary Information
Below is the link to the electronic supplementary material.
Acknowledgments
The authors would like to acknowledge Dr Sînziana Cristea for valuable modelling discussions.
Declarations
Funding
No funding was received for this project.
Conflict of interest
No conflict to declare. The views expressed in this manuscript do not necessarily reflect the position of Finnish Medicines Agency.
Availability of data and material
A .rar file containing all code related to the PBPK framework is included as supplementary information.
Ethics approval
Not applicable.
Consent
Not applicable.
Author contributions
L.B.S.A. and J.G.C.H. designed the study; S.T.T. developed the QSAR models, L.B.S.A. , T.Z., E.B. developed the PBPK framework; L.B.S.A performed the data analysis; L.B.S.A, M.A.A.S., P.V., J.G.C.H. supported interpretation of results; L.B.S.A., S.T.T., J.G.C.H., T.Z., E.B., P.H.G., M.A.A.S., P.V., J.G.C.H. wrote the paper; J.G.C.H. conceived the project; all authors reviewed the paper.
Contributor Information
Linda B. S. Aulin, Email: l.b.s.aulin@lacdr.leidenuniv.nl
J. G. Coen van Hasselt, Email: coen.vanhasselt@lacdr.leidenuniv.nl.
References
- 1.Rybak MJ. Pharmacodynamics: relation to antimicrobial resistance. Am J Infect Control. 2006;34:38–45. doi: 10.1016/j.ajic.2006.05.227. [DOI] [PubMed] [Google Scholar]
- 2.Rodvold KA, Hope WW, Boyd SE. Considerations for effect site pharmacokinetics to estimate drug exposure: concentrations of antibiotics in the lung. Curr Opin Pharmacol. 2017;36:114–123. doi: 10.1016/j.coph.2017.09.019. [DOI] [PubMed] [Google Scholar]
- 3.Rodvold KA, Yoo L, George JM. Penetration of anti-infective agents into pulmonaryepithelial lining fluid. Clin Pharmacokinet. 2011;50:689–704. doi: 10.2165/11592900-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 4.Huang YCT, Piantadosi CA. Alveolar barrier function assessed by hydrophobic and hydrophilic fluorescent solutes in rabbit lung. Respir Physiol Neurobiol. 2002;133:153–166. doi: 10.1016/S1569-9048(02)00150-7. [DOI] [PubMed] [Google Scholar]
- 5.Brillault J, De Castro WV, Couet W. Relative contributions of active mediated transport and passive diffusion of fluoroquinolones with various lipophilicities in a Calu-3 lung epithelial cell model. Antimicrob Agents Chemother. 2010;54:543–545. doi: 10.1128/AAC.00733-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Assmus F, Houston JB, Galetin A. Incorporation of lysosomal sequestration in the mechanistic model for prediction of tissue distribution of basic drugs. Eur J Pharm Sci. 2017;109:419–430. doi: 10.1016/j.ejps.2017.08.014. [DOI] [PubMed] [Google Scholar]
- 7.Bhattacharya J, Matthay MA. Regulation and repair of the alveolar-capillary barrier in acute lung injury. Annu Rev Physiol. 2013;75:593–615. doi: 10.1146/annurev-physiol-030212-183756. [DOI] [PubMed] [Google Scholar]
- 8.Peteranderl C, Sznajder JI, Herold S, Lecuona E. Inflammatory responses regulating alveolar ion transport during pulmonary infections. Front Immunol. 2017;8:1–8. doi: 10.3389/fimmu.2017.00446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Quinton LJ, Walkey AJ, Mizgerd JP. Integrative physiology of pneumonia. Physiol Rev. 2018;98:1417–1464. doi: 10.1152/physrev.00032.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fischer H, Widdicombe JH. Mechanisms of acid and base secretion by the airway epithelium. J Membr Biol. 2006;211:139–150. doi: 10.1007/s00232-006-0861-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kiem S, Schentag JJ. Interpretation of antibiotic concentration ratios measured in epithelial lining fluid. Antimicrob Agents Chemother. 2008;52:24–36. doi: 10.1128/AAC.00133-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Välitalo PAJ, Griffioen K, Rizk ML, Visser SAG, Danhof M, Rao G, van der Graaf PH, van Hasselt JGC. Structure-based prediction of anti-infective drug concentrations in the human lung epithelial lining fluid. Pharm Res. 2016;33:856–867. doi: 10.1007/s11095-015-1832-x. [DOI] [PubMed] [Google Scholar]
- 13.Aulin LBS, Valitalo PA, Rizk ML, Visser SAG, Rao G, van der Graaf PH, van Hasselt JGC. Validation of a model predicting anti-infective lung penetration in the epithelial lining fluid of humans. Pharm Res. 2018;35:26. doi: 10.1007/s11095-017-2336-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gaohua L, Wedagedera J, Small BG, Almond L, Romero K, Hermann D, Hanna D, Jamei M, Gardner I. Development of a multicompartment permeability-limited lung PBPK model and its application in predicting pulmonary pharmacokinetics of antituberculosis drugs. CPT Pharmacomet Syst Pharmacol. 2015;4:605–613. doi: 10.1002/psp4.12034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Eriksson J, Thörn H, Lennernäs H, Sjögren E. Pulmonary drug absorption and systemic exposure in human: predictions using physiologically based biopharmaceutics modeling. Eur J Pharm Biopharm. 2020;156:191–202. doi: 10.1016/j.ejpb.2020.09.004. [DOI] [PubMed] [Google Scholar]
- 16.Hartung N, Borghardt JM. A mechanistic framework for a priori pharmacokinetic predictions of orally inhaled drugs. PLoS Comput Biol. 2020;16:1–24. doi: 10.1371/journal.pcbi.1008466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tylutki Z, Polak S. A four-compartment PBPK heart model accounting for cardiac metabolism-model development and application. Sci Rep. 2017;7:1–11. doi: 10.1038/srep39494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Krombach F, Münzing S, Allmeling AM, Gerlach JT, Behr J, Dörger M. Cell size of alveolar macrophages: an interspecies comparison. Environ Health Perspect. 1997;105(Suppl):1261–1263. doi: 10.1289/ehp.97105s51261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Caputo GR, Kondo C, Masui T, Geraci SJ, Sullivan MMO, Higgins CB. Rigth and left lung perfusion: in vitro and in vivo validation with obliqe-angle, velocity-encoded cine MR imaging. Radiology. 1991;180:693–698. doi: 10.1148/radiology.180.3.1871279. [DOI] [PubMed] [Google Scholar]
- 20.Bryan AC, Bentivoglio LG, Beerel F, Macleish H, Zidulka A, Bates DV. Factors affecting regional distribution of ventilation and perfusion in the lung. J Appl Physiol. 1964;19:395–402. doi: 10.1152/jappl.1964.19.3.395. [DOI] [PubMed] [Google Scholar]
- 21.Grumetto L, Russo G, Barbato F. Immobilized artificial membrane HPLC derived parameters vs PAMPA-BBB data in estimating in situ measured blood-brain barrier permeation of drugs. Mol Pharm. 2016;13:2808–2816. doi: 10.1021/acs.molpharmaceut.6b00397. [DOI] [PubMed] [Google Scholar]
- 22.Yamamoto Y, Välitalo PA, Huntjens DR, Proost JH, Vermeulen A, Krauwinkel W, Beukers MW, Van Den Berg DJ, Hartman R, Wong YC, Danhof M, Van Hasselt JGC, De Lange ECM. Predicting drug concentration-time profiles in multiple CNS compartments using a comprehensive physiologically-based pharmacokinetic model. CPT Pharmacomet Syst Pharmacol. 2017;6:765–777. doi: 10.1002/psp4.12250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Saleh MAA, Loo CF, Elassaiss-Schaap J, De Lange ECM. Lumbar cerebrospinal fluid-to-brain extracellular fluid surrogacy is context-specific: insights from LeiCNS-PK3.0 simulations. J Pharmacokinet Pharmacodyn. 2021;48:725–741. doi: 10.1007/s10928-021-09768-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Taylor AE, Gaar KA. Estimation of equivalent pore radii of pulmonary capillary and alveolar membranes. Am J Physiol. 1970;218:1133–1140. doi: 10.1152/ajplegacy.1970.218.4.1133. [DOI] [PubMed] [Google Scholar]
- 25.Kim YH, Kim KJ, D’Argenio DZ, Crandall ED. Characteristics of passive solute transport across primary rat alveolar epithelial cell monolayers. Membranes (Basel). 2021;11:1–26. doi: 10.3390/membranes11050331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Avdeef A, Nielsen PE, Tsinman O. PAMPA—a drug absorption in vitro model: 11. Matching the in vivo unstirred water layer thickness by individual-well stirring in microtitre plates. Eur J Pharm Sci. 2004;22:365–374. doi: 10.1016/j.ejps.2004.04.009. [DOI] [PubMed] [Google Scholar]
- 27.Renkin EM. Filtration, diffusion, and molecular sieving through porous cellulose membranes. J Gen Physiol. 1954;38:225–243. [PMC free article] [PubMed] [Google Scholar]
- 28.Korson L, Drost-hansen W, Millero FJ. Viscosity of water various temperatures (1968).
- 29.Gotfried MH, Danziger LH, Rodvold KA. Steady-state plasma and intrapulmonary concentrations of levofloxacin and ciprofloxacin in healthy adult subjects. Chest. 2001;119:1114–1122. doi: 10.1378/chest.119.4.1114. [DOI] [PubMed] [Google Scholar]
- 30.Cook PJ, Andrews JM, Wise R, Honeybourne D, Moudgil H. Concentrations of OPC-17116, a new fluoroquinolone antibacterial, in serum and lung compartments. J Antimicrob Chemother. 1995;35:317–326. doi: 10.1093/jac/35.2.317. [DOI] [PubMed] [Google Scholar]
- 31.Rodvold KA, Danziger LH, Gotfried MH. Steady-state plasma and bronchopulmonary concentrations of intravenous levofloxacin and azithromycin in healthy adults. Antimicrob Agents Chemother. 2003;47:2450–2457. doi: 10.1128/AAC.47.8.2450-2457.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Rotoli BM, Barilli A, Visigalli R, Ferrari F, Frati C, Lagrasta CA, Di Lascia M, Riccardi B, Puccini P, Asta VD. Characterization of ABC Transporters in EpiAirwayTM, a cellular model of normal human bronchial epithelium; Int J Mol Sci. 2020 Apr 30;21(9):3190. [DOI] [PMC free article] [PubMed]
- 33.Yao X, Ye F, Zhang M, Cui C, Huang B, Niu P, Liu X, Zhao L, Dong E, Song C, Zhan S, Lu R, Li H, Tan W, Liu D. In vitro antiviral activity and projection of optimized dosing design of hydroxychloroquine for the treatment of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) Clin Infect Dis. 2020;71:732–739. doi: 10.1093/cid/ciaa237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Martins-Filho PR, Ferreira LC, Heimfarth L, Araújo AAS, Quintans-Júnior LJ. Efficacy and safety of hydroxychloroquine as pre-and post-exposure prophylaxis and treatment of COVID-19: A systematic review and meta-analysis of blinded, placebo-controlled, randomized clinical trials. Lancet Reg Health Am. 2021;2:100062. doi: 10.1016/j.lana.2021.100062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kashour Z, Riaz M, Garbati MA, AlDosary O, Tlayjeh H, Gerberi D, Hassan Murad M, Rizwan Sohail M, Kashour T, Tleyjeh IM. Efficacy of chloroquine or hydroxychloroquine in COVID-19 patients: a systematic review and meta-analysis. J Antimicrob Chemother. 2021;76:30–42. doi: 10.1093/jac/dkaa403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kolli AR, Calvino-Martin F, Hoeng J. Translational modeling of chloroquine and hydroxychloroquine dosimetry in human airways for treating viral respiratory infections. Pharm Res. 2022 doi: 10.1007/s11095-021-03152-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Derendorf H. Excessive lysosomal ion-trapping of hydroxychloroquine and azithromycin. Int J Antimicrob Agents. 2020;55:106007. doi: 10.1016/j.ijantimicag.2020.106007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wolowich WR, Kwon YM. Simulation of drug in the lung can be misleading. Clin Infect Dis. 2021;72:1677–1678. doi: 10.1093/cid/ciaa907. [DOI] [PubMed] [Google Scholar]
- 39.R.C. Team. R: A Language and Environment for Statistical Computing (2021)
- 40.Mueller M, Sawchuk RJ, Zeitlinger M, Müller M, Joukhadar C. Lung microdialysis—a powerful tool for the determination of exogenous and endogenous compounds in the lower respiratory tract (Mini-Review). AAPS J. 7. [DOI] [PMC free article] [PubMed]
- 41.Heiskanen T, Heiskanen T, Kairemo K. Development of a PBPK model for monoclonal antibodies and simulation of human and mice PBPK of a radiolabelled monoclonal antibody. Curr Pharm Des. 2009;15:988–1007. doi: 10.2174/138161209787581968. [DOI] [PubMed] [Google Scholar]
- 42.R.W. Van Dyke. Acidification of rat liver lysosomes: quantitation and comparison with endosomes. Am J Physiol Cell Physiol. 1993; 265. [DOI] [PubMed]
- 43.Johansen B, Bjortuft O, Boe J. Static lung volumes in healthy subjects assessed by helium dilution during occlusion of one mainstem bronchus. Thorax. 1993;48:381–384. doi: 10.1136/thx.48.4.381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Assmus F, Francis L, Plumb J, Damian V, Gertz M, Houston JB, Galetin A. In vitro and in silico tools to assess extent of cellular uptake and lysosomal sequestration of respiratory drugs in human alveolar macrophages. Mol Pharm. 2017 doi: 10.1021/acs.molpharmaceut.6b00908. [DOI] [PubMed] [Google Scholar]
- 45.Weibel ER. Lung morphometry: the link between structure and function. Cell Tissue Res. 2017;367:413–426. doi: 10.1007/s00441-016-2541-4. [DOI] [PubMed] [Google Scholar]
- 46.Wiśniewski JR, Hein MY, Cox J, Mann M. A “proteomic ruler” for protein copy number and concentration estimation without spike-in standards. Mol Cell Proteom. 2014;13:3497–3506. doi: 10.1074/mcp.M113.037309. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.