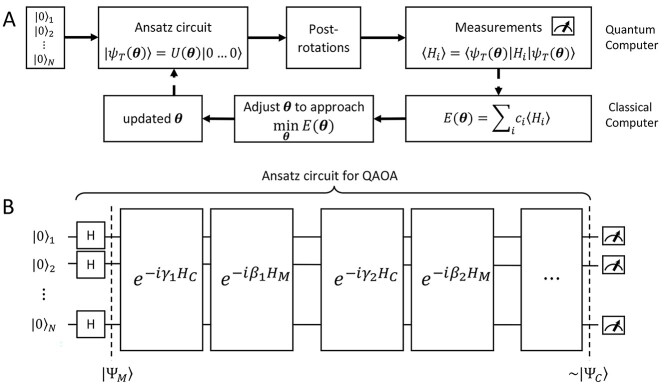
Figure 3.
(A) Scheme of VQE. Starting from the initialized state where all the qubits are set to 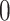 (
(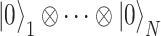 ), a trial state (commonly called with the German word ansatz) is prepared using a quantum circuit (the ansatz circuit) whose operations are parametrized by a set of variational parameters
), a trial state (commonly called with the German word ansatz) is prepared using a quantum circuit (the ansatz circuit) whose operations are parametrized by a set of variational parameters 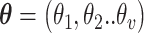 (e.g. single-qubit rotations, each parameterized by some angle
(e.g. single-qubit rotations, each parameterized by some angle 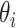 ). The choice of the ansatz circuit determines which subspace of the general Hilbert space can be spanned by the variational procedure. The electronic structure Hamiltonian can be written as a sum of appropriately weighted products of single-qubit operations, i.e.
). The choice of the ansatz circuit determines which subspace of the general Hilbert space can be spanned by the variational procedure. The electronic structure Hamiltonian can be written as a sum of appropriately weighted products of single-qubit operations, i.e. 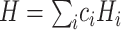 , where
, where 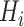 is, for example,
is, for example, 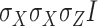 , implying
, implying 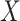 rotation on the first and second qubits,
rotation on the first and second qubits, 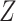 rotation on the third, identity on the fourth, in a four-qubit register. Each
rotation on the third, identity on the fourth, in a four-qubit register. Each 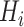 term is evaluated separately, and post-rotations can be needed to rotate the single qubits to the measurement basis (in the example, the first two qubits need to be rotated in order to measure
term is evaluated separately, and post-rotations can be needed to rotate the single qubits to the measurement basis (in the example, the first two qubits need to be rotated in order to measure 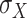 ). Thanks to these operations, the expectation value of each product in the Hamiltonian can be written in terms of the probabilities of each possible outcome, implying that, for each global cycle, a sufficiently large number of state preparation and measurement cycles needs to be performed (Hamiltonian averaging). The measurements (i.e. the probabilities of each possible outcome) are passed to the training/optimization subroutine on the classical computer, whose task is to calculate
). Thanks to these operations, the expectation value of each product in the Hamiltonian can be written in terms of the probabilities of each possible outcome, implying that, for each global cycle, a sufficiently large number of state preparation and measurement cycles needs to be performed (Hamiltonian averaging). The measurements (i.e. the probabilities of each possible outcome) are passed to the training/optimization subroutine on the classical computer, whose task is to calculate 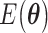 and provide a new set of
and provide a new set of 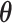 based on the previous history of
based on the previous history of 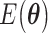 values. The cycle is repeated until convergence. (B) The ansatz circuit for the Quantum Approximate Optimization Algorithm (QAOA) used in the QuASer (see main text). The QUBO problem of finding the optimal solution of a quadratic Hamiltonian is recast into a quantum annealing form
values. The cycle is repeated until convergence. (B) The ansatz circuit for the Quantum Approximate Optimization Algorithm (QAOA) used in the QuASer (see main text). The QUBO problem of finding the optimal solution of a quadratic Hamiltonian is recast into a quantum annealing form 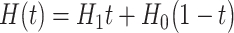 , where
, where 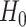 is the ‘simple’ mixing Hamiltonian
is the ‘simple’ mixing Hamiltonian 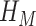 whose ground state is the equal superposition of all basis states
whose ground state is the equal superposition of all basis states 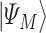 and is obtained after the application of Hadamard gates to all the qubits.
and is obtained after the application of Hadamard gates to all the qubits. 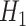 is the cost Hamiltonian
is the cost Hamiltonian 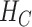 and is defined in such a way that its ground state
and is defined in such a way that its ground state 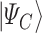 corresponds to the QUBO solution. The adiabatic evolution that would lead from
corresponds to the QUBO solution. The adiabatic evolution that would lead from 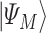 to
to 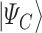 is approximated by the sequential application of
is approximated by the sequential application of 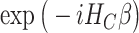 and
and 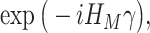 where the
where the 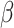 s and
s and 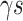 , the ‘time steps’ of the evolution, are the variational parameters (i.e. the
, the ‘time steps’ of the evolution, are the variational parameters (i.e. the 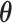 set) to be optimized by the classical subroutine.
set) to be optimized by the classical subroutine.