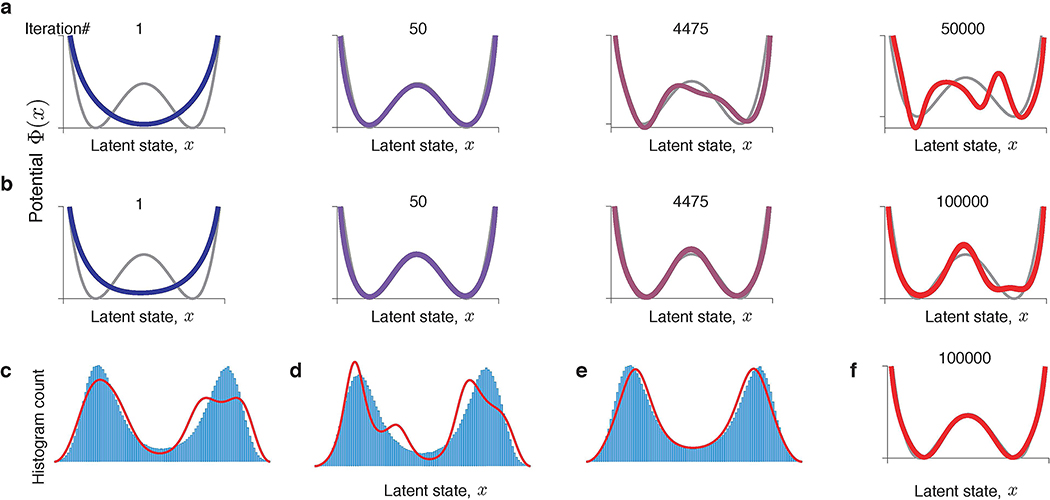
Extended Data Fig. 1. Overfitting does not occur with infinite training data.

(a) A series of models produced by the gradient-descent, when the same finite set of data is used throughout the optimization. Substantial overfitting is observed. (b) Same as a, but optimization is performed with spikes resampled on each iteration of the gradient-descent from a fixed latent trajectory (latent trajectory is the same as in a). Overfitting is still observed. (c) Histogram of the latent trajectory (normalized as probability density) and discovered equilibrium probability density (at iteration 100,000) from the simulation in b. Overfitted model contains features that are not present in the latent trajectory. (d) Same as c, but for a different latent trajectory. Spurious features in c and d are different. (e) Same as c, but with resampling both the latent trajectory and spikes on each iteration of the gradient-descent. No signs of overfitting are observed. (f) After 100,000 iterations, the inferred potential for the simulation in e still perfectly matches the ground truth. These simulations confirm that overfitting emerges largely due to Poisson noise (compare a and b), although noise in the latent trajectory also contributes to overfitting (compare b and f). No overfitting occurs when both spikes and latent trajectory are resampled on each gradient-descent iteration. In all panels, the training data contains ~10,000 spikes generated from a double-well potential.