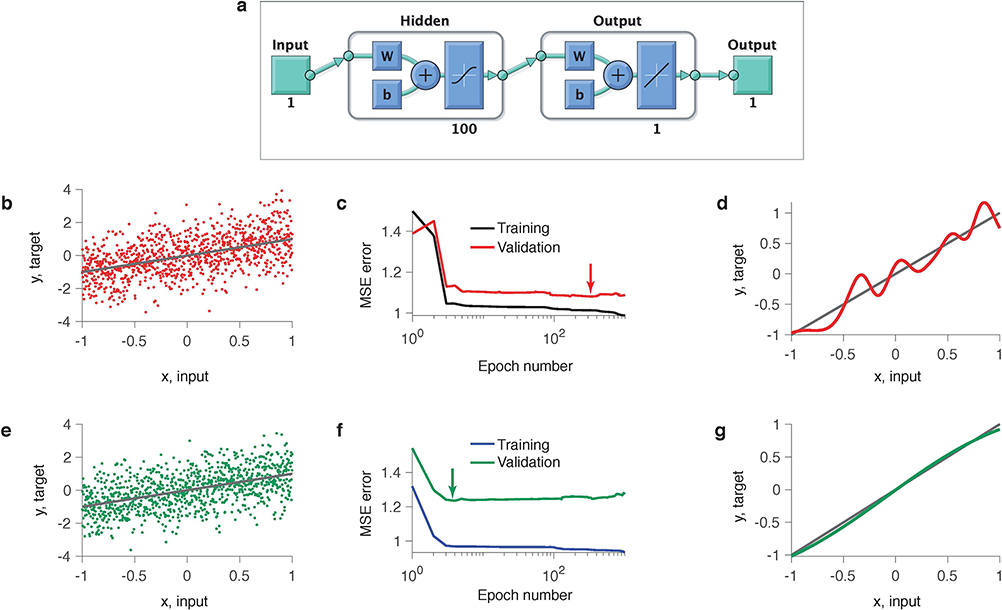
Extended Data Fig. 2. A feedforward neural network exhibits generalization plateaus and overfitting in model selection.

We trained a shallow feedforward neural network (1 hidden layer, 100 neurons, the total number of parameters is 301) on a regression problem. The noisy data set of 1,000 samples was generated from a linear model y = x + 0.2ξ, where $\xi ~𝒩(0,1)$. The network was trained using Matlab Deep Learning toolbox, which runs stochastic gradient-descent with early stopping regularization. We initialized all parameters (weights and biases) from the normal distribution with zero mean and variance 0.01. We verified that our results did not depend on a particular realization of the initial parameters. (a) Network architecture. (b) Example data set (dots) along with the linear ground-truth model (line). (c) Training and validated mean squared errors (MSEs) over the optimization epochs. Long plateau in the validated MSE indicates that many models generalize equally well. Arrow indicates the minimum of the validated MSE, i.e. the model with the best generalization. (d) The model with the best generalization (red line, corresponds to arrow in c) contains spurious features not present in the linear ground-truth model (grey line). (e) Same as b but for a different data sample from the same ground-truth model. (f) Same as c, but for the data sample in e. (g) Same as d, but for the data sample in e. The model with the best generalization (green line, corresponds to arrow in f) closely matches the ground-truth model (grey line).