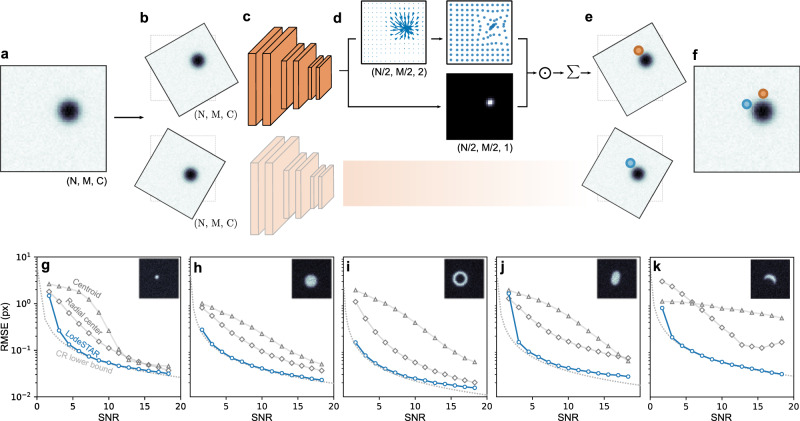
Fig. 1. LodeSTAR single-shot training and performance.

a Example image of a single particle used to train the neural network (N × M pixels, C color channels). b Two copies of the original image transformed by translations and rotations. c The transformed images are fed to a convolutional neural network. d The neural network outputs two tensors (feature maps), each with N/2 × M/2 pixels: One (top) is a vector field where each pixel represents the direction and distance from the pixel itself to the object (top left, blue arrows), which is then transformed so that each pixel represents the direction and distance of the object from the center of the image (top right, blue markers). The other tensor (bottom) is a weight map (normalized to sum to one) corresponding to the contribution of each element in the top feature map to the final prediction. e These two tensors are multiplied together and summed to obtain a single prediction of the position of the object for each transformed image. f The predicted positions are then converted back to the original image by applying the inverse translations and rotations. The neural network is trained to minimize the distance between these predictions. g–k LodeSTAR performance on 64 px × 64 px images containing different simulated object shapes: g point particle, (h) sphere, (i) annulus, (j) ellipse, and (k) crescent. Even though LodeSTAR is trained on a single image for each case (found in the corresponding inset), its root mean square error (RMSE, blue circles) approaches the Cramer-Rao (CR) lower bound (dotted gray line), and significantly outperforms traditional methods based on the centroid²³ (gray triangles) or radial symmetry²⁴ (gray diamonds), especially at low signal-to-noise ratios (SNRs). Interestingly, even in the crescent case (k), where there is no well-defined object center, LodeSTAR is able locate it to within a tenth of pixel.