Abstract
Road crashes are a major problem for traffic safety management, which usually causes flash crowd traffic with a profound influence on traffic management and communication systems. In 2020, the sudden outbreak of the novel coronavirus disease (COVID-19) pandemic led to significant changes in road traffic conditions. In this paper, by analyzing crash data from 2016 to 2020 and new COVID-19 case data in 2020, we find that the average crash severity and crash deaths during this period (a rapid increase of new COVID-19 cases in 2020) are higher than those in previous four years. Hence, it is necessary to exploit a novel road crash risk prediction model for such an emergency. We propose a novel data-adaptive fatigue focal loss (DA-FFL) method by fusing fatigue factors to establish a road crash risk prediction model under the scenario of large-scale emergencies. Finally, the experimental results demonstrate that DA-FFL performs better than the other typical methods in terms of area under curve (AUC) and false alarm rate (FAR) for imbalanced data. Furthermore, DA-FFL has better prediction performance in convolutional neural networks-long short-term memory (CNN-LSTM).
Keywords: COVID-19, Crash risk prediction, Flash crowd traffic, Data imbalance, Large-scale emergencies
1. Introduction
Traffic accidents have become the eighth leading cause of death in the world and cost three percent of Gross Domestic Product (GDP) in most of the countries [1]. Safety is the biggest concern in an intelligent transportation system. According to official statistics [1], around 1.35 million people died in traffic accidents every year. Furthermore, traffic accidents can cause traffic jams to form a flash crowd traffic that are supply–demand mismatching problems for communication resources and communication congestion problems. When a traffic jam occurs, vehicle-to-vehicle distance becomes very close, which leads to a significant increase in traffic density [2]. People in cars use their cell phones more frequently than normal during a traffic jam in a fixed field, which will increase the communication overhead of the roadside communication base stations.
To reduce the occurrence of traffic accidents, Chen et al. studied the crash risk prediction of road sections as an important factor for traffic management to control traffic accurately [3]. It can not only reduce the incidence of road traffic accidents but also provide much more auxiliary information for decision-making. However, Zhang et al. think that the road traffic environment has become more complex and variable due to the rapid increase in the number of vehicles each year [4].
On the other hand, Yang et al. [5] found that COVID-19 has strong contagiousness and uncontrollable variability and it has been developed into a global public health issue in a very short period. The COVID-19 pandemic has affected various industries, such as healthcare, the global economy, education, tourism, transportation [6], and so on. During the COVID-19 pandemic, people travel less by public transportation [7]. As a result, the proportion of car trips, destinations, and routes have changed more than the period before the COVID-19 pandemic. Due to the dramatically affection for the transportation systems [8], the methods for road crash risk prediction face new challenges. First, crash data becomes much more unbalanced [9] during COVID-19. Unbalanced data can cause models to be biased toward most classes, which makes risk prediction much harder.
In order to study in-depth the impact of the COVID-19 pandemic on traffic, Adanu et al. analyze crash data during the COVID-19 pandemic and found that traffic, vehicle mileage, and the number of crashes have all dropped significantly during COVID-19 in [10], and the number of fatal crashes has increased.
Li et al. analyzed empirical spatiotemporal road traffic congestion during the COVID-19 pandemic [11], which found that traffic congestion had an upward trend after the pandemic. Furthermore, Zhou et al. analyzed the response policy during the COVID-19 outbreak and found that the prevention policy would have a new impact on urban traffic [12]. However, the existing works about road crash risk prediction models cannot meet the unique requirement of stable and accurate.
To address the above challenges, this research aims to fuse multi-source data to analyze the characteristics of road crash data during COVID-19 and exploit the intrinsic connections between COVID-19 and road traffic crashes.
Meanwhile, we propose an improved focal loss function to deal with imbalanced crash data by considering fatigue factors in the transportation system. The details of this proposal will be discussed in Section 4.3. The main contributions of this work can be summarized as follows,
-
•
We analyzed Covid-19 data and crash data from 2016 to 2020 and find that the average severity and number of fatalities per crash increased during the COVID-19 pandemic compared to the pre-COVID-19 period.
-
•
To the best of our knowledge, this is a pioneering study exploring road crash risk prediction models under specific emergencies (COVID-19).
-
•
We propose to introduce a fatigue factor to improve the focal loss function, which further overcomes the problem of data imbalance.
-
•
The proposed DA-FFL approach can reduce flash crowd traffic caused by road crashes and maintain road traffic safety and communication efficiency during large-scale emergencies.
The rest of this paper is organized as follows: In Section 2, the researches in road crash risk prediction and traffic safety during the COVID-19 pandemic are presented. In Section 3, we introduce the sources of experimental data and some new findings after data analysis. In Section 4, we illustrate the main techniques used in this study, and the fatigue factor and DA-FFL method proposed by this paper. In Section 5, we explain how to process the data and the results are analyzed. In Section 6, we discuss the differences from existing work, and implications of this study and the challenge faced. Finally, Section 7 concludes this paper.
2. Related work
To improve the safety of road traffic, researchers employ many different methods to predict road crash risk. In this section, we shall discuss the most related works from three aspects: traditional machine learning based methods, deep learning based methods, and traffic safety during COVID-19.
2.1. Machine learning based methods
In the field of road crash risk prediction, machine learning methods have emerged as a promising approach to train accurate and robust statistical models from data. support vector machines (SVM) is a traditional machine learning method with a solid theoretical foundation that performs well in solving small samples, nonlinearity, regression, and binary classification problems with high dimensionality. Yu et al. used the SVM model with radial basis kernel function (RBF) to achieve better results in crash risk prediction with a small sample size [13].
Logistic regression is also a classical machine learning method, which is simple and easy to understand and has good model interpretability. It can demonstrate the impact of different features on the final result from the weights of the features and also have a small memory resource consumption. Cheng et al. [14] proposed a crash risk prediction model based on the extended Logit method with real-time traffic flow data as input for urban freeways. Guo et al. [15] analyzed the relationship between traffic flow, risky driving behavior, and traffic crash risk. The authors also built a model to predict traffic crash risk based on logistic regression. Meanwhile, Alrukaibi et al. [16] proposed to predict freeway crash frequency by using a mixed logit model.
In addition, K-Nearest Neighbor (K-NN) is also good at dealing with classification problems and is suitable for classifying rare events without estimating parameters. Dimitrijevic et al. [17] used a comparative analysis of various machine learning methods such as Bayesian Logistics Regression, K-NN, and Random Forest to conclude that the use of driver behavior data can improve the predictive performance of the model. Random Forests, a widely used algorithm in machine learning, is an integrated learning method based on Bagging that can handle classification and regression well. Zhai et al. fused traffic monitoring data, foggy accident data, and road geometry data to identify and rank the most important variables by using the random forest. Then, the authors built a crash risk prediction model for freeways under foggy conditions based on Bayesian logistic regression [18].
Machine learning methods based on statistical learning methods have shown stable performance in road crash prediction, traditional machine learning methods are usually not the best choice due to the face of increasing amounts of data and more complex tasks [19].
2.2. Deep learning based methods
With the rapid development of deep learning (DL) technologies, many DL algorithms have been applied to crash risk prediction since deep neural networks have a strong ability for feature extraction.
Moosavi et al. [20] first created a large-scale public accident information database (US-Accidents) including traffic events, weather data, points of interest and time. Then, the authors proposed a deep accident prediction neural network (DAP) that significantly improves the prediction of rare crash cases. To learn the Spatio-temporal characteristics of the road traffic data, Bao et al. [21] proposed a Spatio-temporal convolution long-term and short-term memory network (STCL-net). This proposal fuses the Global Positioning System (GPS) data of taxis with other multi-source data training models, and well predicted the short-term crash risk in New York City.
Although the neural network model is able to predict the road crash risk, the real road crash data only occupies a small part of the massive traffic data. It shows that the highly unbalanced data set affects the learning ability of the model since the number of crash samples and non-crash samples in the data used for research often varies greatly. To solve the problem of data imbalance for the deep learning prediction model, Li et al. [22] used the synthetic minority over-sampling technique (SMOTE) to sample a few samples outside the model. They proposed an CNN-LSTM based crash risk prediction model for urban roads, which is superior to the traditional machine learning model in sensitivity and false alarm rate. Yu et al. [23] fused five minutes of multi-source data into time slices with spatial information, enhanced the weight of a few samples from the inside of the model by using the focus loss function [24]. They designed a convolutional neural network based crash risk prediction model.
2.3. Researches on traffic safety during COVID-19
Many works have studied the corresponding emergency plans based on the data during COVID-19.
Adanu et al. [10] showed that although the traffic volume, vehicle mileage, and the number of traffic accidents decreased significantly during COVID-19, the number of fatal traffic accidents increased. In addition, the work [25] researched the changes of bicycle crashes in Arlington, Virginia before and after COVID-19 and finds that the crash risk of bicycle travel increased during COVID-19. Meanwhile, after studying the data on road crashes, deaths and minor injuries in Greece during COVID-19, Sekadakis et al. found that the number of deaths and minor injuries in road crashes increased significantly in the first month of COVID-19 in [9].
In such situations, a sustainable and stable communication network is very important in the event of large-scale emergencies [26]. However, as aforementioned, most of the current studies have only analyzed the changes in traffic crashes during the COVID-19 pandemic without considering flash crowd traffic caused by crashes and the communication congestion on the road during large-scale emergencies. Hence, we explore road crash changes during large-scale emergencies and attempt to develop a crash risk prediction model for large-scale emergency scenarios.
The related literature is summarized in Table 1, including data types, models, and road types.
Table 1.
Related work summary.
| Author | Year | Data | Prediction model | Road type |
|---|---|---|---|---|
| Yu et al. | 2013 | Traffic data | SVM | Colorado Mountainous freeway |
| Cheng et al. | 2022 | Traffic flow | EL | Shanghai Urban freeway |
| Guo et al. | 2021 | Driving behavior | LR | China G15 freeway |
| Alrukaibi et al. | 2021 | Crash data | MLM | Kuwait highways |
| Dimitrijevic et al. | 2022 | Multi-source data | BLR,K-NN | New Jersey highway |
| Zhai et al. | 2020 | Multi-source data | BLR | California freeways |
| Moosavi et al. | 2019 | US-Accidents | DAP | The United States |
| Bao et al. | 2019 | Multi-source data | STCL net | New York City Roads |
| Li et al. | 2020 | Multi-source data | CNN-LSTM | Urban roads in Orlando |
| Yu et al. | 2020 | Multi-source data | CNN | Shanghai urban expressway |
| Adanu et al. | 2021 | Traffic data,COVID-19 | ML,LC-MNL | Alabama roadways |
| Monfort et al. | 2021 | COVID-19,Bicycle crash | FMM | Arlington bike lanes |
| Sekadakis et al. | 2021 | Traffic data,COVID-19 | SARIMA | Greece roadways |
3. Dataset and analysis
3.1. Dataset
The data used in this research are illustrated as follows.
-
•
Traffic Data
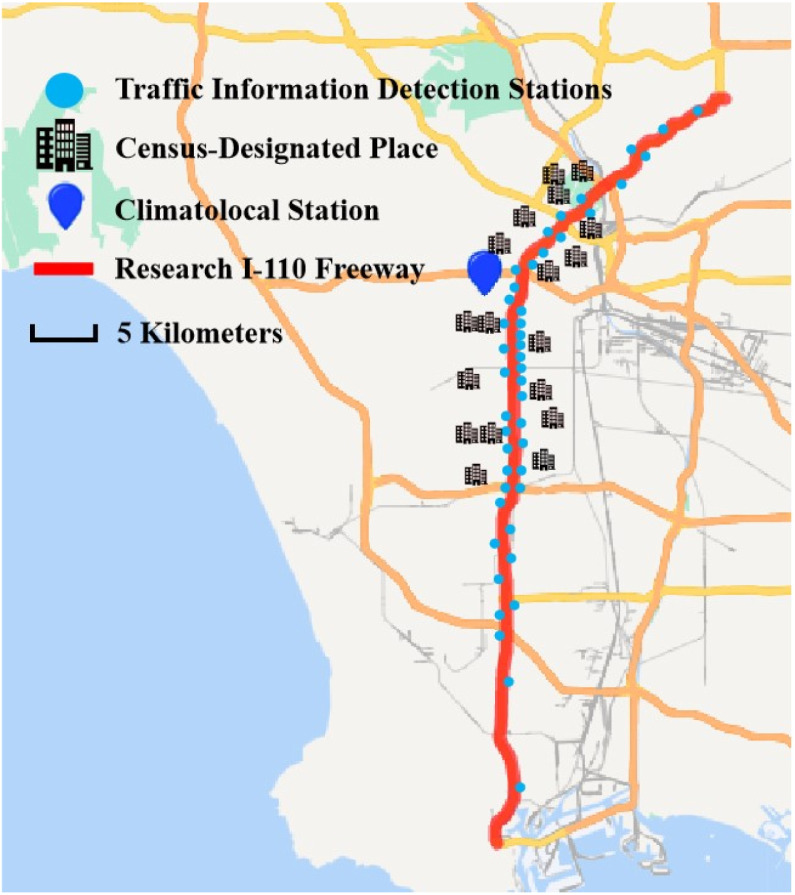
In this study, we select the Interstate 110 (I-110) freeway whose total length is 48.4 km, which has more accidents among the freeways in Los Angeles. As shown in Fig. 1, the visualization illustrates the data of southbound and northbound roads through the freeway Performance Measurement System (PeMS) maintained by the California Department of Transportation (CalTrans) [27], ranging from 22 and 23 traffic detection stations. It includes various features such as traffic flow, speed, road occupancy, vehicle miles traveled (VMT) and vehicle hours traveled (VHT). However, it is difficult to directly utilize the traffic data for each lane recorded by the detection station for the model [18] due to the random noise. Hence, the data are aggregated into 5-minute intervals instead of every 30 s.
-
•
Weather Data
We obtain weather data from Los Angeles International Airport which is nearby the I-110 freeway, from the National Oceanic and Atmospheric Administration (NOAA) [28]. It includes features such as visibility, rainfall, temperature, humidity and air pressure. All the weather data are updated hourly. The details of the selection of the weather features will be explained later.
-
•
Crash Data
Road crash data on the I-110 freeway is obtained in the Transportation Injury Mapping System (TIMS) [29] developed by the University of California, Berkeley. Road crash data include specific crash time, location, severity, number of casualties, crash type, etc. For an in-depth analysis of the crash data characteristics during COVID-19 in 2020, we collect all accident data from January to December 2016–2020.
-
•
COVID-19 Case Data As shown in Fig. 1, we select 18 Census-Designated Places (CDPs) located along the I-110 freeway with a high population density, which are also the sections with the highest number of crashes. The selected data include new confirmed cases of COVID-19 per day from March 2020 to December 2020 in 18 CDPs. The COVID-19 case data in this study are publicly available [30], the detailed information on CDPs is shown in Table 2.
Fig. 1.
Research I-110 freeway in Los Angeles.
Table 2.
Census-designated place and population.
| CDP | Population | CDP | Population |
|---|---|---|---|
| Elysian Park | 5712 | Exposition Park | 44917 |
| Angelino Heights | 2502 | West Vernon | 53644 |
| Wholesale District | 36129 | South Park | 37961 |
| Chinatown | 8021 | Harvard Park | 37935 |
| Temple-Beaudry | 39482 | Florence-Firestone | 47445 |
| Westlake | 59355 | Vermont Knolls | 17200 |
| Downtown | 27507 | Vermont Vista | 41186 |
| Pico-Union | 41842 | Century Palms/Cove | 33766 |
| University Park | 27456 | Figueroa Park Square | 8721 |
3.2. Data analysis and findings
First, we analyze the crash situation during the years from 2016 to 2020 in general and then summarize crash data in Table 3 where we calculate the number of crashes, the number of injured, and the number of deaths specifically for each year. It can be seen that there are more deaths caused by road crashes in 2020 than in the previous four years, with 11, 8, 1, and 12 more than from 2016 to 2019, respectively. Meanwhile, we calculate the average number of the above three items and compute the overall severity which means the accumulation of the severity value for each crash. The severity of the crash takes values from 1 to 4, and the smaller number indicates a more serious crash. In Table 3, we can see that the average number of injured people, death, and severity show a different pattern in 2020, compared with the cases in the other four years.
Table 3.
Comparison of crash data from 2016 to 2020.
| Year | 2016 |
2017 |
2018 |
2019 |
2020 |
|---|---|---|---|---|---|
| NO. of crashes | 730 | 901 | 842 | 869 | 795 |
| Total injuries | 1013 | 1290 | 1106 | 1196 | 1168 |
| Average NO. of injured | 1.388 | 1.432 | 1.314 | 1.376 | 1.469 |
| Total deaths | 5 | 8 | 15 | 4 | 16 |
| Average NO. of deaths | 0.007 | 0.009 | 0.018 | 0.005 | 0.020 |
| Total severity | 2697 | 3322 | 3074 | 3214 | 2287 |
| Average severity | 3.691 | 3.687 | 3.651 | 3.699 | 3.631 |
In 2020, the number of injured in the average of a crash peaked at 1.469, the death toll per average of a crash peaked at 0.02, and crash severity reached a five-year high of 3.631(the smaller the number, the more serious). From the above data, it can be seen that the internal characteristics of road traffic crashes have changed in 2020 under the influence of COVID-19.
Next, we exploit to compare the crash data from January to December for the five years from 2016 to 2020 since the number of cars and population do not change much in the nearly five years, so as to the road conditions which makes comparison results of the crash data meaningful. As depicted in Fig. 2, a square represents the crash situation for a day. The number of crashes for each day is represented by different colors, where the color near blue shows smaller cases and close to red represents more crash cases. The number of crashes counts the crash caused by normal automobiles, pedestrians, bicycles, motorcycles, and trucks, but do not include crashes related to alcohol and drugs. Fig. 2 shows that the crashes are more evenly distributed from 2016 to 2019 than in 2020. And it is obvious that the blue squares are mainly clustered in the months of March to July, November, and December of 2020, indicating that lower crashes occurred during this period than in the previous four years. Meanwhile, we know that the I-110 freeway is located in an area where the new cases of COVID-19 began to appear in March. Therefore, the drop-down of crashes during this period may have a strong correlation with COVID-19.
Fig. 2.
Number of crashes per day from 2016 to 2020.
To further verify the above correlation, we count the number of new COVID-19 cases each day for the 18 CDPs from March 13 to December 31, 2020, and show the results in Fig. 3. Between March and July, there is a growing trend in the number of new cases each day over time. Then, it is followed by a gradual decrease from August to October. After that, the number of new COVID-19 cases per day exploded in November and December due to colder weather and several other factors. There are even 1,890 new cases on December 16. We find that the two intervals of rapid growth in Fig. 3 with an increasing trend of new daily cases (March to July, November to December) correspond strictly to the two intervals with a much smaller number of crashes in Fig. 2, and this phenomenon is most obvious at the beginning of COVID-19. It means that there is a negative correlation between the number of crashes and the number of new cases per day, which can confirm that the number of crashes has a strong correlation with COVID-19.
Fig. 3.
Total number of new COVID-19 cases per day in 2020 in 18 CDPs.
To further explore the deeper impact of the COVID-19 pandemic on road crashes, we make a more detailed comparison of the crash data from 2016 to 2020. As illustrated in Fig. 4, the average of each crash’s severity and the number of deaths from January to December are plotted.
Fig. 4.
Average severity and deaths of a crash for January to December from 2016 to 2020.
Firstly, Fig. 4(a) compares the average severity per crash for each month. In the vast majority of months during these five years, the average severity exceeds 3.5. In particular, crashes are more severe during periods from March to May and November to December 2020, in which the two lowest values occur in April and December at 3.4 and 3.42, respectively. Moreover, these two periods are not only the worst in 2020, but they are worse than these two periods in the previous four years. This is consistent with the findings in the previous section.
Secondly, Fig. 4(b) represents the average number of deaths per crash for each month. The number of deaths in 2020 is concentrated in a period of rapid growth in COVID-19 cases, with these two periods (March to May, November to December) accounting for 56.25% of the year’s deaths. Specifically, March and November are the two months with the highest average number of deaths per crash in 2020 at 4.3% and 6.5%, respectively, which coincides with the beginning of two rapid growth intervals of new COVID-19 cases.
Based on the above analysis, we find that when the number of new cases of COVID-19 increases rapidly, the number of crashes decreases significantly, but on average the severity of each crash and the number of deaths are increasing. As a result, it can be determined that COVID-19 has a serious impact on road traffic crashes. And the crash data from March to May, the period most affected by COVID-19, is utilized for further study.
3.3. Motivation of this study
The COVID-19 pandemic has changed traffic patterns, including but not limited to a reduction in the number of trips and a change in the purpose and route of trips. Based on the above new findings, the most important impact on traffic safety is the apparent reduction in the number of crashes during COVID-19, and a significant increase in the average severity and number of deaths per crash, especially during the period of rapid growth in the number of new COVID-19 cases per day. In addition, communication resources are more important than usual during the COVID-19 pandemic.
Reducing traffic crashes can decrease flash crowd traffic caused by traffic jams, further diminish communication congestion, and maintain an efficient road communication environment during large-scale emergencies. Therefore, there is an urgent need to study the changes in road crashes in the context of the COVID-19 pandemic and develop crash risk prediction models based on data during COVID-19 to provide decision support for traffic management authority (TMA) to optimize traffic systems, reduce the occurrence of traffic crashes, prevent flash crowd traffic on roads, and address the root causes of communication problems due to traffic crashes.
4. Methodology
This section describes the main theories and techniques, including SMOTE and focal loss functions, as well as the proposed fatigue factor.
4.1. Synthetic minority oversampling technique
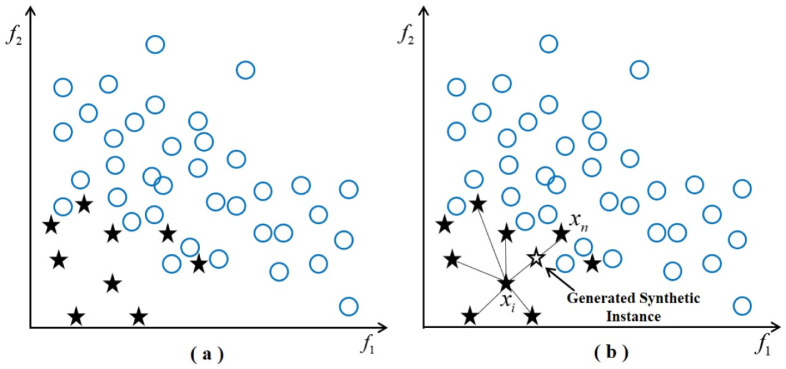
SMOTE as a data synthesis method is only applied to the training data-set. The test data will not be synthesized, so the test data can still reflect the real information [21]. There are several types of SMOTE, including regular SMOTE, ADASYN, Borderline-SMOTE, SVMSMOTE, and SMOTE+ENN [31]. The conventional SMOTE has been chosen mostly [21] since it shows good performance in road crash risk prediction.
Specifically, the entire data sample is defined as , and the subset denotes the minority class sample. The definition of SMOTE can be written by Eq. (1):
| (1) |
where denotes the th minority class sample, , and is one of the K-nearest neighbors for , is the newly generated sample.
To create a synthetic sample , we calculate the Euclidean distance between a minority class sample B and one of its random nearest neighbors. The second item at the right of Eq. (1) denotes the weighted Euclidean distance with a random number between. Therefore, the synthetic sample generated according to Eq. (1) is a point on a line segment along the minority class sample and a randomly selected K-nearest neighbor .
The specific process of the new sample synthesized by SMOTE is illustrated in Fig. 5.
Fig. 5.
The illustration of SMOTE data generation based on Euclidean distance (K = 6).
4.2. Fatigue factor
In this study, we analyze the crash data for each year and find that the crash severity and the number of crashes are very similar to the distribution of the 24-hour driver fatigue index mentioned in [32]. To verify this finding, we divide the crash number and crash severity data from March to May 2020 into 24 hourly segments for cumulative statistics. For comparison, we normalize the above two sets of data and the driver fatigue data from [32] by Min–Max normalization, respectively.
To depict the similarity between the crash number curve, crash severity curve, and driver fatigue curve, we introduce dynamic time warping (DTW) [33] to calculate the similarity.
Firstly, let denote the fatigue index, denote the number of crashes, and denote the total crash severity. ; ; . All three sequences are 24-hour values, so . is the Euclidean distance matrix between the points of and . is the Euclidean distance matrix between the points of and .
Then search for a minimum path from to , and search for a minimum path from to . and are obtained by a dynamic programming algorithm. The dynamic programming algorithm is based on the following recurrence relation.
| (2) |
| (3) |
where and denote the cumulative distance from the start point to the current element. and denote the distance of the current element, which is the distance between and , and , respectively. The shortest path from the start point to the current element is the length of the shortest path from the start point to the previous element plus the value of the current element
Therefore, the DTW values of Q and C, Q and S are the minimum values of the cumulative distance of the path elements, respectively, which are calculated by Eq. (4), and the results are shown in Fig. 6.
| (4) |
where denote the th element on , denote the th element on . and are the shortest path from to and from to , respectively.
Fig. 6.
DTW-based curve similarity comparison.
The DTW values calculated from the crash number curve and driver fatigue curve and from the crash severity curve and driver fatigue curve are 2.727 and 2.754, respectively. These results show that the two sets of curves are very similar and fully indicate that road crashes are highly correlated with driver fatigue. Therefore, it is necessary to take driver fatigue into account in road crash risk prediction. However, we did not collect data directly describing driver fatigue during the COVID-19 epidemic, so the crash severity curve with the smaller DTW value is selected instead of the fatigue curve and is denoted as the fatigue factor for subsequent studies.
4.3. Fatigue-FL and DA-FFL method
The focal loss function was originally proposed by Lin et al. in [24] and has been widely used in subsequent studies on data imbalance.
| (5) |
In this study, we use the fatigue factor to modify the focal loss function. Eq. (6) is the improved loss function denoted as the fatigue focal loss (Fatigue-FL) function, where each period time corresponds to a fatigue factor value.
| (6) |
where N is the number of samples predicted, i represents the th sample, indicates the label of the th real sample, and . means crash occurrence, indicates no crash occurrence. denotes the probability that the th sample is predicted to be a crash, and . Weighting factor , focusing parameter follows . The focal loss shall evolve into the -weighted cross entropy when .
is the fatigue factor that corresponds to each hour. In our proposed Fatigue-FL, the value of is automatically adjusted according to the fatigue time feature of the crash sample, the values of at different time intervals are shown in Fig. 6. We define a correction function to achieve adaptive adjustment of the value. When the sample is in a fatigue-prone period the corresponding fatigue factor will achieve a higher value, and the loss value of the Fatigue-FL function will be reduced.
Fig. 7 shows the values of the fatigue factor and the values after processing, the blue and red dots indicate the original values. For the sake of observation, we used the Savitzky–Golay filter [34] for smoothing blue and red dashed lines. When the value of is high, the lower value can be obtained after processing, which makes the loss value lower and makes the model pay more attention to the crash sample. Similarly, when the value of is low, it makes the model pay less attention to the crash sample. In brief, we incorporate the fatigue factor into the focal loss to obtain the Fatigue-FL proposed in this study, which is a loss function that can adaptively adjust the degree of attention to the crash sample as the fatigue level varies for each time interval. The specific performance is verified by subsequent experiments.
Fig. 7.
Fatigue factor and the correction function.
Furthermore, we propose a method DA-FFL for predicting road crash risk based on the Fatigue-FL function, as depicted in Fig. 8. When the ratio of positive to negative samples is greater than 0.05, the Fatigue-FL function is used in the neural network model. However, when the ratio of positive to negative samples is less than 0.05, the positive samples are first processed using SMOTE before using the fatigue focus loss function. This approach adaptively selects the optimal processing according to the degree of data imbalance to maintain the predictive performance of the model.
Fig. 8.
Data adaptive fatigue-focal loss method based crash risk prediction model.
5. Experiments
5.1. Data preprocessing
Based on the results of the data analysis in the previous section, the data used in this research is for 92 days from March 1, 2020, to May 31, 2020. Because this is the first three months of the COVID-19 pandemic, where the impact of road traffic is most pronounced. The initial data needs to be cleaned before the experiment. Due to the uncontrollable factors of the detector technology, the initial data is often missing randomly. Traffic data has time continuity, the average of the two data before and after the missing time is filled in as the missing position.
There are many types of weather data, but not every type of data is suitable for model training. It is necessary to select the best weather data to enhance the model’s accuracy. We use the Pearson correlation coefficient [35] to perform correlation analysis on the weather data and use the Kolmogorov–Smirnov (K–S) [36] test to verify the normal distribution of the weather data. As depicted in Fig. 9, the Pearson correlation coefficient values close to −1 are negative correlations and close to 1 indicate positive correlations. If the correlation between the two features is high, it will be verified with the normal distribution, Table 4 presents the results of the normal distribution of weather features. In this table, Remove the feature data that do not satisfy the normal distribution or the normal distribution is not obvious. Because data close to the normal distribution will be more conducive to improving the training of the model. Therefore, we choose the four indicators that best represent the normal distribution as the standard deviation (SD), skewness, kurtosis, and K–S test, respectively. The SD of precipitation reaches a minimum of 0.087, the skewness of WetBulbTemperature (WBTemperature) is closest to 0, the kurtosis of humidity is closest to 0 and the K–S test of pressure has a minimum -value of 0.067. Furthermore, we also consider the impact of actual weather conditions on the risk of road crashes, visibility is taken into account. After the above screening methods, we finally select the five weather characteristics of temperature, precipitation, humidity, pressure and visibility.
Fig. 9.
Correlation analysis of weather features.
Table 4.
Weather data normal distribution test.
| Variable | Median | Mean | SD | Skewness | Kurtosis | K-S |
|---|---|---|---|---|---|---|
| DPTemperature | 30 | 24.67 | 14.354 | −0.546 | −1.27 | 0.276 |
| DBTemperature | 16 | 15.93 | 10.690 | 0.322 | −0.65 | 0.121 |
| WBTemperature | 57 | 56.99 | 5.048 | −0.143 | −0.20 | 0.067 |
| Precipitation | 0 | 0.01 | 0.087 | 12.841 | 193.73 | 0.473 |
| Humidity | 63 | 61.36 | 15.054 | −0.680 | 0.21 | 0.080 |
| Pressure | 29.77 | 29.78 | 0.093 | 0.235 | −0.48 | 0.067 |
| Visibility | 1 | 2.59 | 2.555 | 2.015 | 4.32 | 0.313 |
| WindDirection | 0 | 157.15 | 241.02 | 1.513 | 0.99 | 0.317 |
| WindGustSpeed | 0 | 0.28 | 2.278 | 8.234 | 67.32 | 0.534 |
| WindSpeed | 0 | 2.11 | 2.790 | 1.139 | 0.82 | 0.349 |
For the crash data, we first locate the crash position and then find the two nearest traffic detection stations upstream and downstream respectively. Then the weather data and the traffic data of the detection station are time-aligned. As depicted in Fig. 10, the traffic data of the two detection stations are integrated to train the AI model. As studied in [37], the data between 10 and 15 min before crash time can achieve better crash prediction ability than other time periods. Thus, we label the data of 15 min before the crash time as the crash data. Meanwhile, the crash can be caused by alcohol and drugs, and the crash data is cleaned since such crashes are caused by human factors and are not in the scope of this study. Furthermore, most of the crashes between alcohol and drugs are concentrated in the 00:00–6:00 time period, and the vehicles on the road during this time period are often very rare. Based on this, we remove the data from the time period 00:00–6:00, and the fatigue factor for 6:00–24:00 is retained. Traffic on nearby roads is briefly affected after each crash, and traffic data during this period tends to be highly volatile, so we also removed this data within 60 min after each crash.
Fig. 10.
Crash location and upstream&downstream detection stations.
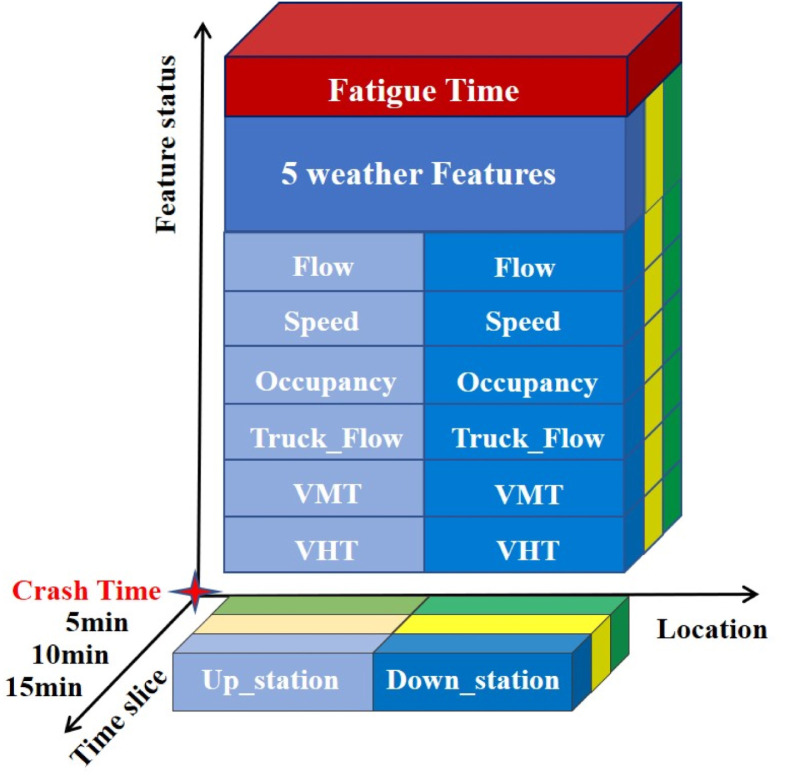
After the above processing, the shape of the experimental data is (893002, 3, 18), in which 892796 is the total number of samples, including 309 crash samples and 892693 non-crash samples. As shown in Fig. 11, the relationship between crash samples and non-crash samples for the entire data sample is illustrated in the time dimension. Fig. 12 shows the structure of each sample, which contains three 5-minute time slices, and each time slice is fused by 6 upstream traffic features, 6 downstream traffic features and 6 downstream traffic features, 5 weather features, and 1 fatigue time distribution feature.
Fig. 11.
The relationship between positive and negative samples in the direction of time.
Fig. 12.
Experimental data sample structure.
5.2. Method assessment
The conventional accuracy evaluation methods cannot meet the requirements of the road crash prediction task since the crash and non-crash samples are very imbalanced. Hence, we exploit to evaluate our model using several methods as follows.
The confusion matrix summarizes the data samples according to the real category and the category predicted by the model. The confusion matrix of the binary classification is a table with two rows and two columns, as shown in Table 5. True negative (TN) means to correctly predict a negative sample, that is, to predict a negative sample as a negative sample, false positive (FP), false negative (FN) and true positive (TP) also have the same representation.
Table 5.
Confusion matrix.
| True\Predicted | Non_crashes | Crashes |
|---|---|---|
| Non_crashes | TN | FP |
| Crashes | FN | TP |
FAR represents the rate at which negative samples are predicted to be positive samples. True positive rate (TPR), means that the correct rate is predicted in all positive samples. The receiver operating characteristic (ROC) curve is often used to evaluate the prediction performance of the binary classification model [38], which can reflect the trend of FPR and TPR when the model selects different thresholds. The AUC value is used as the area under the ROC curve to evaluate the predictive performance of the model [39]. The closer the AUC value is to 1, the better the predictive performance of the model.
5.3. Experimental results
In this section, we use long short-term memory (LSTM) [40] to verify the effectiveness of Fatigue-FL, and then the Fatigue-FL is used in three models to verify the performance of different models for road crash risk prediction during COVID-19. The main structure of our model is CNN and LSTM, including the input layer, 1D convolutional layer, average pooling layer, LSTM layer and fully connected layer. The detail of the CNN-LSTM model architecture for DA-FFL is depicted in Table 6. In the Fatigue-FL function with , , and the optimizer chooses adam.
Table 6.
CNN-LSTM model structure for DA-FFL.
| Layer | Output shape |
|---|---|
| Input layer | 3,18 |
| Convolution1D | None, 3, 64 |
| AveragePooling1D | None, 3, 64 |
| LSTM | None, 64 |
| Dense | None, 20 |
| Dense | None, 2 |
Firstly, we take 6 methods of dealing with data imbalance for comparison experiments, which are none(No method is used), random oversampling, SMOTE, focal Loss, Fatigue-FL, Fatigue-FL&SMOTE (SMOTE and Fatigue-FL are used on the exterior and interior of the model, respectively).
The experimental results for FAR and AUC are shown in Table 7 and 8, respectively. The AUC values at all scales after random oversampling are lower than None’s, the reason might be that random oversampling generates a lot of duplicate data. After the experimental data are processed by SMOTE, the FAR results are significantly better than the none on all 6 proportions and better than random oversampling on most proportions. Meanwhile, the AUC values are improved to different degrees on all 6 proportions, which indicates that SMOTE can effectively enhance the features of the samples. Focal loss has high FAR values for all scales except at 1:10 where it performs better, but the AUC values are higher relative to the previous methods, which indicates that focal loss can effectively reduce the impact of unbalanced data in road crash risk prediction.
Table 7.
False alarm rate experimental results.
| Methods | Crash:Non-crash |
|||||
|---|---|---|---|---|---|---|
| 1:2 | 1:5 | 1:10 | 1:20 | 1:100 | 1:200 | |
| None | 0.144 | 0.491 | 0.436 | 0.528 | 0.475 | 0.599 |
| Randon Oversampling | 0.558 | 0.491 | 0.460 | 0.489 | 0.280 | 0.349 |
| SMOTE | 0.354 | 0.349 | 0.296 | 0.467 | 0.448 | 0.503 |
| Focal Loss | 0.500 | 0.730 | 0.230 | 0.525 | 0.550 | 0.582 |
| Fatigue-FL | 0.138 | 0.348 | 0.143 | 0.406 | 0.534 | 0.238 |
| SMOTE+Fatigue-FL | 0.612 | 0.058 | 0.273 | 0.402 | 0.029 | 0.114 |
Table 8.
AUC value experimental results.
| Methods | Crash:Non-crash |
|||||
|---|---|---|---|---|---|---|
| 1:2 | 1:5 | 1:10 | 1:20 | 1:100 | 1:200 | |
| None | 0.671 | 0.661 | 0.638 | 0.624 | 0.599 | 0.578 |
| Random Oversampling | 0.652 | 0.639 | 0.602 | 0.616 | 0.598 | 0.603 |
| SMOTE | 0.678 | 0.671 | 0.635 | 0.647 | 0.638 | 0.614 |
| Focal Loss | 0.678 | 0.707 | 0.694 | 0.655 | 0.641 | 0.628 |
| Fatigue-FL | 0.686 | 0.712 | 0.710 | 0.692 | 0.674 | 0.654 |
| SMOTE&Fatigue-FL | 0.693 | 0.702 | 0.736 | 0.694 | 0.673 | 0.668 |
When using Fatigue-FL, the FAR is lowest at data ratios of 1:2, 1:10 and the AUC value is highest at 1:5, 1:100, indicating that it shows that the Fatigue-FL function further improves the performance compared to focal Loss. However, this advantage becomes gradually smaller as the proportion of negative samples increases. Finally, the overall performance of SMOTE&Fatigue-FL is slightly lower than Fatigue-FL when the data ratio is lower than 1:10, but the overall performance is slightly higher than Fatigue-FL starting from 1:20. This also suggests that using SMOTE and Fatigue-FL separately inside and outside the model will lead to further improvements in overall model performance as the proportion of positive and negative samples gradually increases. The above experimental results can prove that the proposed DA-FFL method can effectively solve the effect of data imbalance.
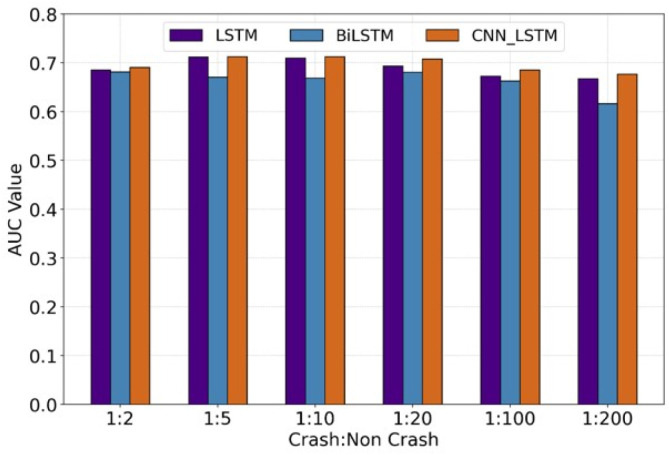
Next, we apply DA-FFL to LSTM, BiLSTM, and CNN-LSTM models and select the suitable model for DA-FFL through performance evaluation. Based on the proposed DA-FFL method, the model comparison section uses the Fatigue-FL loss function at data proportions of 1:2, 1:5, and 1:10, at data proportions of 1:20, 1:100 and 1:200 the data is first processed appropriately with SMOTE and then the Fatigue-FL loss function is used. The experimental results are shown in Fig. 13, where CNN-LSTM performs better than the other two models for different proportions of data with DA-FFL.
Fig. 13.
AUC values of LSTM, BiLSTM and CNN-LSTM.
5.4. Application scenarios
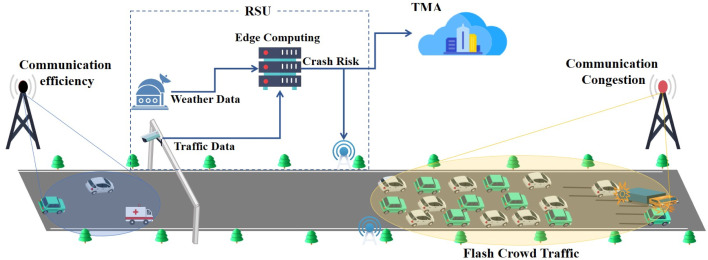
Traffic crash is one of the major reasons for the occurrence of traffic jam, thereby causing flash crowd traffic, which further leads to a sudden high overhead of communication for the neighbor base stations, as depicted in Fig. 14.
Fig. 14.
Relationship between models and flash crowd traffic and communication congestion.
Therefore, our proposal, DA-FFL, can be applied to the edge computing of roadside units (RSU) with the following reasons. First, edge servers are in charge of the prediction of crash risk information through real-time weather data and traffic data. Then, the predicted crash risk information is dispensed to nearby vehicles for future actions through road–vehicle communication. Finally, the crash risk information is uploaded to the cloud for precise regulation by the traffic management authority (TMA).
Therefore, real-time crash risk can be provided to help drivers or autonomous vehicles to make more rational decisions. Our approach can reduce traffic crashes and improves road safety by predicting road crash risk. Meanwhile, it can reduce the flash crowd traffic caused by crashes, thus reducing the incidence of local roadside communication base station congestion and ensuring safe and smooth road and communication during emergencies.
6. Discussion
COVID-19 is a global problem that has affected various industries. The most direct impact on traffic is that people travel less and fewer vehicles travel on the road, but we found a deeper intrinsic impact by analyzing traffic data and infection case data during the COVID-19 pandemic. Therefore, we propose a new method to predict the risk of road crashes under large-scale emergencies, which can help TMA to improve their management capabilities and also prevent the formation of flash crowd traffic, which can lead to local communication congestion along roads.
The theoretical significance lies in the discovery of changes in traffic safety during the COVID-19 pandemic, and we first integrate the fatigue factor into the crash risk prediction model and propose a crash risk prediction model under large-scale emergency scenarios. It provides ideas and directions for future researchers to pay more attention to the impact of large-scale emergency events on traffic. The practical significance is that the research results can be used in traffic management to reduce the flash crowd traffic caused by accidents, thereby reducing the incidence of local roadside communication base station congestion and ensuring the safe and smooth flow of roads during emergencies.
Currently, there are many new research hotspots and discoveries in the field of road crash risk prediction. With the development of vehicle–road cooperation technology and autonomous driving technology, the crash risk prediction of vehicle groups will become important. However, there is no practical application for the mobile vehicle population on the road, so our study focuses on the crash risk of the whole road section.
This paper proposes innovative approaches while facing some challenges. Traffic characteristics may vary from road to road at different times, and models developed for one road cannot be directly used to predict crash risk predictions for another road. Similarly, models built based on data during the COVID-19 pandemic may not yield the same results for ordinary periods, making it a challenge to use migration learning for emergency management to help with large-scale emergencies like COVID-19. Of course, our research also faces some other challenges, such as data imbalance, conducting a larger study, etc., which are worthy of continued in-depth research.
7. Conclusion
In this paper, we identify anomalies of the crash data during the 2020 COVID-19 pandemic through data analysis. By comparing the annual average data from 2016 to 2020, we find that there is the highest number of deaths and injuries of per crash in 2020. In further analysis, we find that when the number of daily new COVID-19 cases increases rapidly, the overall number of crashes decreases. During this period, however, the average crash severity is worse than in the previous four years, and the average number of deaths per crash is higher. This is particularly evident from March to May, which coincides with the first three months of the appearance of 18 CDPs for confirmed cases of COVID-19. Subsequently, we build a road crash risk prediction model for specific large-scale emergency scenarios. Based on the data from March to May 2020, we propose fatigue-factor to further construct Fatigue-FL and DA-FFL to improve the predictive performance of the model.
Through the comparison experiments of different models, CNN-LSTM is more suitable for the proposal DA-FFL compared to LSTM and BiLSTM. And the proposed method can alleviate the flash crowd traffic on road and communication congestion on communication systems caused by road crash. In future work, we will further improve the overall performance of the model.
CRediT authorship contribution statement
Junbo Wang: Conception and design of study, Writing – original draft, Writing – review & editing. Xiusong Yang: Conception and design of study, Acquisition of data, Analysis and/or interpretation of data, Writing – original draft, Writing – review & editing. Songcan Yu: Acquisition of data. Qing Yuan: Analysis and/or interpretation of data. Zhuotao Lian: Writing – review & editing. Qinglin Yang: Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work is supported with National Nature Science Foundation of China, No. 62072485, and Guangdong Basic and Applied Basic Research Foundation, China No. 2022A1515011294. All authors approved the version of the manuscript to be published.
Data availability
The data that has been used is confidential.
References
- 1.World Health Organization, et al. World Health Organization; 2018. Global Status Report on Road Safety 2018: Summary: Technical Report. [Google Scholar]
- 2.Graham D.J. Variable returns to agglomeration and the effect of road traffic congestion. J. Urban Econ. 2007;62(1):103–120. [Google Scholar]
- 3.Chen Z., Qin X. A novel method for imminent crash prediction and prevention. Accid. Anal. Prev. 2019;125:320–329. doi: 10.1016/j.aap.2018.07.011. [DOI] [PubMed] [Google Scholar]
- 4.Zhang Y., Li C., Liu Q.E., Wu W. The socioeconomic characteristics, urban built environment and household car ownership in a rapidly growing city: evidence from Zhongshan, China. J. Asian Archit. Build. Eng. 2018;17(1):133–140. [Google Scholar]
- 5.Yang L., Liu S., Liu J., Zhang Z., Wan X., Huang B., Chen Y., Zhang Y. COVID-19: immunopathogenesis and immunotherapeutics. Signal Transduct. Target. Ther. 2020;5(1):1–8. doi: 10.1038/s41392-020-00243-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yao Y., Geara T.G., Shi W. Impact of COVID-19 on city-scale transportation and safety: an early experience from Detroit. Smart Health. 2021;22 doi: 10.1016/j.smhl.2021.100218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jenelius E., Cebecauer M. Impacts of COVID-19 on public transport ridership in Sweden: Analysis of ticket validations, sales and passenger counts. Transp. Res. Interdiscip. Perspect. 2020;8 doi: 10.1016/j.trip.2020.100242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hu Y., Barbour W., Samaranayake S., Work D. 2020. Impacts of Covid-19 mode shift on road traffic. arXiv preprint arXiv:2005.01610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sekadakis M., Katrakazas C., Michelaraki E., Kehagia F., Yannis G. Analysis of the impact of COVID-19 on collisions, fatalities and injuries using time series forecasting: The case of Greece. Accid. Anal. Prev. 2021;162 doi: 10.1016/j.aap.2021.106391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Adanu E.K., Brown D., Jones S., Parrish A. How did the COVID-19 pandemic affect road crashes and crash outcomes in Alabama? Accid. Anal. Prev. 2021;163 doi: 10.1016/j.aap.2021.106428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li J., Xu P., Li W. Urban road congestion patterns under the COVID-19 pandemic: A case study in Shanghai. Int. J. Transp. Sci. Technol. 2021;10(2):212–222. [Google Scholar]
- 12.Zhou H., Wang Y., Huscroft J.R., Bai K. Impacts of COVID-19 and anti-pandemic policies on urban transport—an empirical study in China. Transp. Policy. 2021;110:135–149. doi: 10.1016/j.tranpol.2021.05.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yu R., Abdel-Aty M. Utilizing support vector machine in real-time crash risk evaluation. Accid. Anal. Prev. 2013;51:252–259. doi: 10.1016/j.aap.2012.11.027. [DOI] [PubMed] [Google Scholar]
- 14.Cheng Z., Yuan J., Yu B., Lu J., Zhao Y. Crash risks evaluation of urban expressways: A case study in Shanghai. IEEE Trans. Intell. Transp. Syst. 2022 [Google Scholar]
- 15.Guo M., Zhao X., Yao Y., Yan P., Su Y., Bi C., Wu D. A study of freeway crash risk prediction and interpretation based on risky driving behavior and traffic flow data. Accid. Anal. Prev. 2021;160 doi: 10.1016/j.aap.2021.106328. [DOI] [PubMed] [Google Scholar]
- 16.Alrukaibi F., AlKheder S., Sayed T., Alburait A. Injury severity influence factors and collision prediction-A case study on Kuwait highways. J. Transp. Health. 2021;20 [Google Scholar]
- 17.Dimitrijevic B., Khales S.D., Asadi R., Lee J. Short-term segment-level crash risk prediction using advanced data modeling with proactive and reactive crash data. Appl. Sci. 2022;12(2):856. [Google Scholar]
- 18.Zhai B., Lu J., Wang Y., Wu B. Real-time prediction of crash risk on freeways under fog conditions. Int. J. Transp. Sci. Technol. 2020;9(4):287–298. [Google Scholar]
- 19.Janiesch C., Zschech P., Heinrich K. Machine learning and deep learning. Electron. Mark. 2021;31(3):685–695. [Google Scholar]
- 20.S. Moosavi, M.H. Samavatian, S. Parthasarathy, R. Teodorescu, R. Ramnath, Accident risk prediction based on heterogeneous sparse data: New dataset and insights, in: Proceedings of the 27th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, 2019, pp. 33–42.
- 21.Bao J., Liu P., Ukkusuri S.V. A spatiotemporal deep learning approach for citywide short-term crash risk prediction with multi-source data. Accid. Anal. Prev. 2019;122:239–254. doi: 10.1016/j.aap.2018.10.015. [DOI] [PubMed] [Google Scholar]
- 22.Li P., Abdel-Aty M., Yuan J. Real-time crash risk prediction on arterials based on LSTM-CNN. Accid. Anal. Prev. 2020;135 doi: 10.1016/j.aap.2019.105371. [DOI] [PubMed] [Google Scholar]
- 23.Yu R., Wang Y., Zou Z., Wang L. Convolutional neural networks with refined loss functions for the real-time crash risk analysis. Transp. Res. C. 2020;119 [Google Scholar]
- 24.T.-Y. Lin, P. Goyal, R. Girshick, K. He, P. Dollár, Focal loss for dense object detection, in: Proceedings of the IEEE International Conference on Computer Vision, 2017, pp. 2980–2988.
- 25.Monfort S.S., Cicchino J.B., Patton D. Weekday bicycle traffic and crash rates during the COVID-19 pandemic. J. Transp. Health. 2021;23 doi: 10.1016/j.jth.2021.101289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wang J., Wu Y., Yen N., Guo S., Cheng Z. Big data analytics for emergency communication networks: A survey. IEEE Commun. Surv. Tutor. 2016;18(3):1758–1778. [Google Scholar]
- 27.California Department of Transportation J. 2022. Performance measurement system. URL: https://pems.dot.ca.gov. (Accessed 2 June 2022) [Google Scholar]
- 28.National Centers for Environmental Information J. 2022. National oceanic and atmospheric administration. URL: https://www.ncei.noaa.gov. (Accessed 2 June 2022) [Google Scholar]
- 29.Safe Transportation Research and Education Center, University of California, Berkeley J. 2022. Transportation injury mapping system. URL: https://tims.berkeley.edu. (Accessed 2 June 2022) [Google Scholar]
- 30.Los Angeles Times Data and Graphics Department J. 2022. california-coronavirus-data. URL: https://github.com/datadesk/california-coronavirus-data. Accessed: 2 June 2022) [Google Scholar]
- 31.He H., Garcia E.A. Learning from imbalanced data. IEEE Trans. Knowl. Data Eng. 2009;21(9):1263–1284. [Google Scholar]
- 32.Friswell R., Williamson A. Comparison of the fatigue experiences of short haul light and long distance heavy vehicle drivers. Saf. Sci. 2013;57:203–213. [Google Scholar]
- 33.Myers C., Rabiner L., Rosenberg A. Performance tradeoffs in dynamic time warping algorithms for isolated word recognition. IEEE Trans. Acoust. Speech Signal Process. 1980;28(6):623–635. [Google Scholar]
- 34.Press W.H., Teukolsky S.A. Savitzky-golay smoothing filters. Comput. Phys. 1990;4(6):669–672. [Google Scholar]
- 35.Benesty J., Chen J., Huang Y., Cohen I. Noise Reduction in Speech Processing. Springer; 2009. Pearson correlation coefficient; pp. 1–4. [Google Scholar]
- 36.Massey F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Amer. Statist. Assoc. 1951;46(253):68–78. [Google Scholar]
- 37.LeCun Y., Boser B., Denker J.S., Henderson D., Howard R.E., Hubbard W., Jackel L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989;1(4):541–551. [Google Scholar]
- 38.Zweig M.H., Campbell G. Receiver-operating characteristic (ROC) plots: a fundamental evaluation tool in clinical medicine. Clin. Chem. 1993;39(4):561–577. [PubMed] [Google Scholar]
- 39.Bradley A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997;30(7):1145–1159. [Google Scholar]
- 40.Graves A. Supervised Sequence Labelling with Recurrent Neural Networks. Springer; 2012. Long short-term memory; pp. 37–45. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that has been used is confidential.