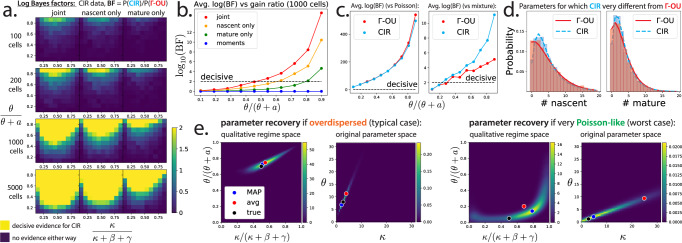
Fig. 3. Model distinguishability and parameter inference.

a Log Bayes factors show models are distinguishable in most of parameter space. Plotted are the average log Bayes factors capped at 2 (a common threshold for decisive evidence in favor of one model). b Models are often strongly distinguishable. A slice of the 1000 cell row of the previous plot (without the cap at 2) for a moderate value of κ/(κ + β + γ). Using both nascent and mature data is better than using either individually, usually by at least an order of magnitude. c It is easy to distinguish the Γ-OU and CIR models from trivial models. Same axes as in (b). Discriminability of Γ-OU and CIR models versus Poisson and mixture models for a somewhat small value of κ (κ/(κ + β + γ) = 0.1), where discriminability is expected to be difficult. d Nascent and mature marginal distributions for the Γ-OU (red) and CIR (blue) models for a maximally distinguishable parameter set. Histograms show synthetic data (5000 cells), while the smooth lines show the exact results. e Bayesian inference of noise model parameters. We sampled the posterior distribution of the parameters of the Γ-OU model (assuming it is known that β = 1, γ = 1.7, and 〈K〉 = 10), given a synthetic data set of 1000 cells. Posteriors are presented in both the qualitative regimes space, and in terms of the original parameters. For very Poisson-like data, posteriors are broad in both spaces, because κ is no longer identifiable. MAP: mode of posterior, avg: average of posterior, true: true parameter values.