Figure 2.

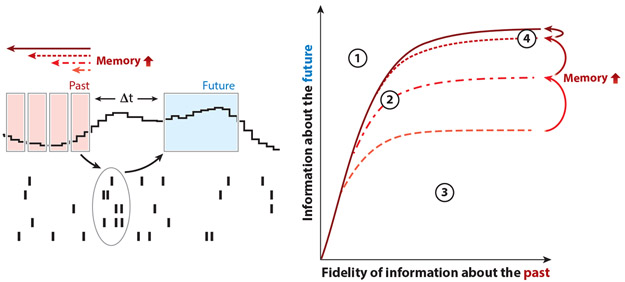
The information bottleneck technique links optimal prediction and memory. The information bottleneck technique is a method for computing the maximal amount of information that a compressed signal, like the brain’s code for the visual stimulus, can carry about a relevant variable in the original input. Within our prediction framework, that relevant feature is the future stimulus. In the diagram, the input is the past stimulus measured within a window of time preceding the neural response (past), and the relevant variable is the future stimulus (future) starting at some time in the future, Δt. For a particular Δt, we can trace out the maximal amount of information that a neural population could possibly carry about the future stimulus given how much information that population encoded about the past stimulus. There are several notable regions in this information plane spanned by the past and future information (left). First (①), there is an inaccessible region: You cannot know more about the future than about the past; i.e., there is no fortune-telling. The brain’s code can occupy any other region in the plane. Second (②), sitting near the bound means that the neural code contains the maximal amount of predictive information possible for a given level of fidelity of past information. Third (③), neural responses that reflect information about the past but fall away from the bound are not optimized for prediction as a consequence of encoding unpredictable parts of the input stimulus. Fourth (④), the saturation point, reflecting the maximal information that you can glean about the future, is set by the correlation structure in the stimulus. It is important to note that memories of the past can, themselves, be faulty. The x axis in the bottleneck plots reflects precisely that fidelity. For a system with a given memory time window, neural systems can be so noisy that they carry no information about the past stimulus (the origin). Conversely, they could represent the past stimulus with high precision (e.g., with finer and finer stimulus resolution, moving outward along the x axis). Increasing the timescale for memory of the past can improve prediction, up to the limits set by the longest correlation times in the stimulus itself (e.g., dashed versus solid lines). In this example, expanding the length of the past stimulus history saturates after the memory of the past is expanded to four blocks of time in the past.