Fig. 1.

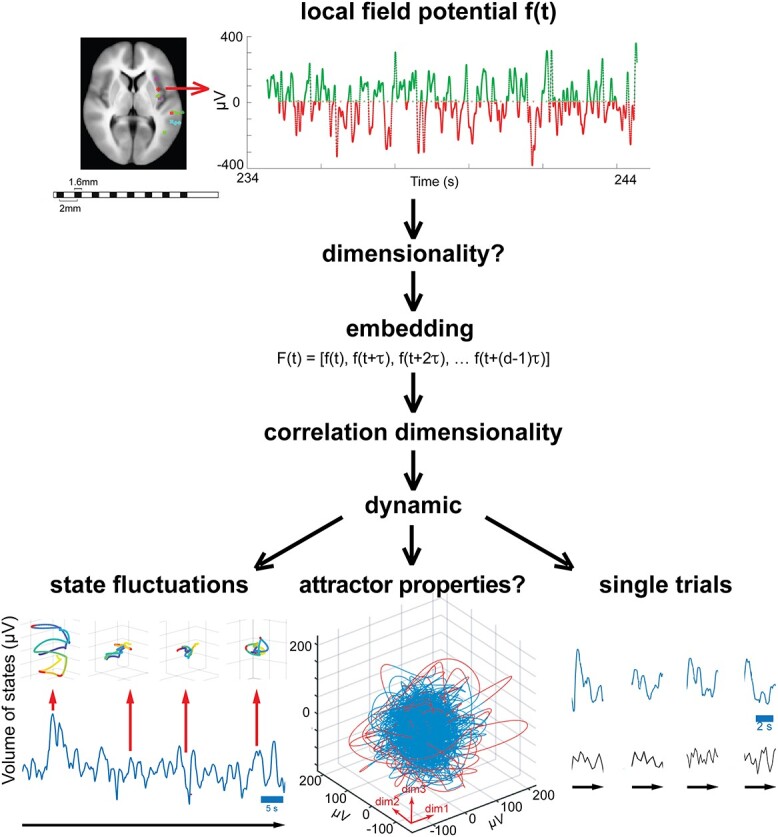
Logic of the analysis. Electrode lead with field potential f(t) sampled at 512 Hz. To find the dynamics of the local networks, we must know the f(t) dimensionality. We first constructed a vector F(t) of f(t) delayed by successive multiples of τ ms (embedding). The dimensionality of F(t) is the number of dimensions needed to achieve an exhaustive description of F(t). We then calculated the correlation dimensionality from this 20-dimensional vector F(t). We then studied the dynamic in state spaces of the found correlation dimension (ranging from 3 to 9). The dynamic consists of continuous state fluctuations, properties maintaining stability and single trial fluctuations. In state space, each point is one local cortical state. The points, 1.95 ms apart, are connected to form one blue—red colored trajectory (60 s long). When the trajectory escapes (red) from the blue dense part, it is rapidly pulled back. This resembles an attractor property, but the dynamics is not attractor dynamics because of the state fluctuations: These 50 ms volumes of evolving states fluctuate continuously, with consequent stretching and contraction of the state trajectories (the 4 examples show 1-s trajectories). Single trials: The volumes from a subset of leads (blue) show correlated expansion and contraction of their evolving state volumes, whereas other leads (black) do not. These properties roughly characterize the local cortical network dynamic.