Evaluation of machine learning methods for covariate data imputation in pharmacometrics

Abstract

Missing data create challenges in clinical research because they lead to loss of statistical power and potentially to biased results. Missing covariate data must be handled with suitable approaches to prepare datasets for pharmacometric analyses, such as population pharmacokinetic and pharmacodynamic analyses. To this end, various statistical methods have been widely adopted. Here, we introduce two machine‐learning (ML) methods capable of imputing missing covariate data in a pharmacometric setting. Based on a previously published pharmacometric analysis, we simulated multiple missing data scenarios. We compared the performance of four established statistical methods, listwise deletion, mean imputation, standard multiple imputation (hereafter “Norm”), and predictive mean matching (PMM) and two ML based methods, random forest (RF) and artificial neural networks (ANNs), to handle missing covariate data in a statistically plausible manner. The investigated ML‐based methods can be used to impute missing covariate data in a pharmacometric setting. Both traditional imputation approaches and ML‐based methods perform well in the scenarios studied, with some restrictions for individual methods. The three methods exhibiting the best performance in terms of least bias for the investigated scenarios are the statistical method PMM and the two ML‐based methods RF and ANN. ML‐based approaches had comparable good results to the best performing established method PMM. Furthermore, ML methods provide added flexibility when encountering more complex nonlinear relationships, especially when associated parameters are suitably tuned to enhance predictive performance.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

Missing covariate data is an important topic in the context of pharmacometric analyses. Currently, covariate imputation is handled with standard statistical methods.

WHAT QUESTION DID THIS STUDY ADDRESS?

Are the machine‐learning (ML) based approaches random forest and artificial neural networks capable to handle missing covariate data in a statistical plausible manner and how do they perform compared to established statistical methods?

WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

We demonstrated that ML‐based approaches can be used to impute missing covariate information for pharmacometric modeling such as population pharmacokinetic analyses. They are largely independent of the underlying relationship and even without optimization, such as parameter tuning, they provide comparable results to the best performing classical statistical methods.

HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

Results from this evaluation study provides useful information on various statistical and ML‐based methods supporting pharmacometricians and clinical pharmacologists in selecting the best suitable method to impute missing covariate data.

INTRODUCTION

Characterizing the behavior of a drug in patient populations of interest is an integral part for efficacious and safe treatments. Pharmacometric analysis of clinical data ¹ , ² , ³ , ⁴ and, in particular, population pharmacokinetic and pharmacodynamic (PK‐PD) analyses is a key contribution to achieving this goal. Pharmacometric models that identify and quantify effects of patients' characteristics (i.e., covariates), on key model parameters, such as volume of distribution and clearance are indispensable for optimizing and personalizing dosing of new and existing medicines in adult and pediatric patients.

A common challenge with clinical data is that there is missing covariate information. ⁵ There can be different reasons for missing entries, and these may influence the structure of missing data and affect pharmacometric analyses. As pharmacometric analyses are used for decision making in drug development and clinical practice, a biased analysis can have a negative impact on patients and must be avoided. As such, it is critical to correctly handle missing covariate data in pharmacometric analyses.

Rubin et al. introduced a set of key definitions for missing data. Data where the occurrence of missing values are assumed to be independent of any variable in the dataset is called missing completely at random (MCAR) ⁶ ; for example, when patients miss a clinical examination due to random public transport breakdowns. If the probability of missing data in one variable is assumed to be related to one or more other observed variables in the dataset, the data are classified as being missing at random (MAR); for example, when older people miss more examinations than younger patients due to more difficulties getting to the hospital. Missing not at random (MNAR) describes data where it is assumed that the missingness depends on unobserved data; for example, when sicker people miss hospital examinations more often than healthy people.

The simplest way of dealing with missing values is called “listwise deletion” (LD) where all entries with missing values are removed from the analysis, resulting in less data being available for the analysis. A more complex approach is to fill in or “impute” missing data so that all patient data, including the imputed values, can then be analyzed. Many different methods are available for imputation, ⁷ , ⁸ which have also been fully or partially implemented in pharmacometrics. ⁹ One prominent imputation method is multiple imputation, ¹⁰ , ¹¹ , ¹² where the missing data are imputed several times to generate multiple “complete” datasets. Each complete dataset is then analyzed separately and the results are combined using so‐called “Rubin's rules”. ¹⁰ This procedure is often preferred because the variance of the estimated parameters in the analysis model are inflated to better consider the uncertainty coming from missing values.

Besides these classical statistical methods, machine learning (ML) has recently become increasingly relevant in many areas of today's scientific and daily life. Several ML methods such as random forest (RF) and artificial neural networks (ANNs) have already been introduced to impute missing values. ¹³ , ¹⁴ , ¹⁵ , ¹⁶ ML‐based methods are mainly data driven and often not based on an explicitly stated parametric model. In this study, the two ML methods—RF and ANN—are investigated and compared with standard statistical methods for their potential to impute missing covariate values in a clinical dataset being prepared for subsequent pharmacometric analysis. Here, we describe the applied ML methods for a broad audience in terms of statistical and pharmacometric experience.

In this study, we investigate four established statistical methods and two ML‐based imputation methods to handle missing covariate data. Because data collection in neonates, infants, and older children is particularly cumbersome and challenging due to difficulties in enrolling study subjects and drawing blood samples, methods to handle missing covariate values may be particularly relevant in this clinical field. As such, we selected a dataset from a previously published study in neonates. ¹⁷ This pediatric dataset provided a population‐specific set of covariates relevant for pharmacometric analysis and evaluation of imputation methods.

METHODS

We performed a simulation study to evaluate and compare four standard statistical imputation methods and two ML‐based imputation methods to handle various levels of missing covariate data in the context of population PK analyses under MCAR and MAR assumptions. The simulation study included the following seven steps, as illustrated in Figure 1: first, obtain descriptive statistics of relevant covariates from the clinical pediatric dataset; second, generate a reference covariate PK dataset with a complete set of clinically relevant covariates for a generic drug with predefined population PK parameters and parameter distributions; third, apply a standard i.v. bolus one‐compartment population PK model to estimate model parameters utilizing reference covariate PK dataset; fourth, generate reduced PK datasets with various levels of missing covariate information; fifth, apply four established statistical methods and two ML‐based methods to impute missing covariate information; sixth, apply same pharmacometric model to estimate model parameters utilizing imputed covariate PK dataset; and seventh, assess and compare performance of investigated imputation methods in terms of model parameter estimations.

FIGURE 1.

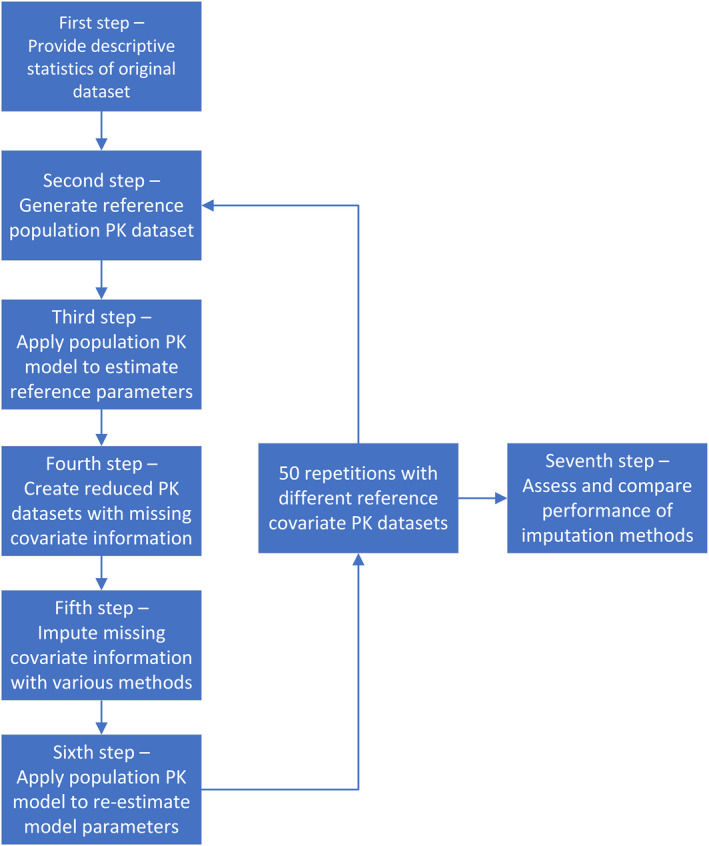
A flow chart of the presented simulation study. PK, pharmacokinetic.

The applied standard i.v. bolus one‐compartment population PK model had the following three key components: population volume of distribution ($V_{\mathrm{pop}}$), population clearance ($\mathrm{C}{\mathrm{L}}_{\mathrm{pop}}$), and one covariate of interest in neonatology, effect of birth weight (BW) on volume of distribution (${\beta }_V$). Steps of the simulation study are described in the following sections.

All simulations and analyses were conducted in R, version 4.0.4, ¹⁸ using an interface to Monolix. ¹⁹

First step – Provide descriptive statistics of original dataset

The presented simulation study was based on a subset of data collected in neonates with extremely low BW (van Donge et al. ¹⁷ ) consisting of 215 neonates with complete BW and birth length (BL) information. BW and BL in this dataset were summarized with a multivariate normal distribution (see Table S1).

Second step – Generate reference covariate population PK dataset

A simulated reference covariate population PK dataset was generated to allow comparison of the different imputation methods. First, the relationship between BW and BL was created. Second, the ${\beta }_V$ was generated depending on the BW. Third, the one‐compartment PK concentration data for a generic drug was simulated for the 215 patients. Fourth and finally, additional covariates were added to the PK dataset.

To investigate whether a method is highly dependent on the relationships in the dataset to impute, two types of relationships between BW and BL were investigated. In datasets with linear relationships, baseline BW and BL values were sampled from the multivariate normal distribution derived from descriptive statistics of BW and BL in the original dataset. In datasets with nonlinear relationships, BL was sampled from the univariate normal distribution observed in the original dataset. To generate nonlinear relationships between BW and BL, the BW was simulated utilizing a maximum effect (E _max) function with Hill coefficient. Two different covariate models relating BW with the ${\beta }_V$ $V$ were investigated.

A linear covariate model was applied according to

$$V=V_{\mathrm{pop}}\left(1+{\beta }_V\left(\mathrm{BW}-\mathrm{B}{\mathrm{W}}_{\mathrm{ref}}\right)\right)e^{{\eta }_V}$$

where $V_{\mathrm{pop}}$ is the population value, ${\beta }_V$ the covariate effect, $\mathrm{B}{\mathrm{W}}_{\mathrm{ref}}=\text{mean}\left(\mathrm{BW}\right)$ the reference value for BW and ${\eta }_V$ a zero mean, normally distributed random variable with SD ${\omega }_V$. Model parameters were set to $V_{\mathrm{pop}}=6$ and ${\beta }_V=0.001$. A nonlinear covariate model was applied according to

$$V=V_{\mathrm{pop}}{\left(\frac{\mathrm{BW}}{\mathrm{B}{\mathrm{W}}_{\mathrm{ref}}}\right)}^{{\beta }_V}{e}^{{\eta }_V}$$

with analogous parameter definitions. In order to have a strong nonlinear relationship in the dataset that cannot be approximated with a linear model, $V_{\mathrm{pop}}$ was set to $6$ and ${\beta }_V$ to $8$. Clearance ($\mathrm{CL}$) was sampled from a log‐normal distribution without a covariate effect.

To rule out the possibility that the results are specific to the model parameter volume of distribution V, the performance of imputation methods was also evaluated with a covariate effect of BW on the other key PK parameter CL. Structural similar linear and nonlinear covariate models were applied as shown above.

The individual serum concentration C(t) of a generic drug was simulated for five timepoints (t = 0, 1, 3, 8, and 12 h) with a PK one‐compartment i.v. model:

$$C\left(t\right)=\frac{d}{V}{e}^{-\frac{\mathrm{Cl}}{V}t},$$

where d is the applied dose. This simple PK model with only one covariate effect was selected in order to allow a clear evaluation based only on a small set of model parameters.

To simulate a realistic setting, gestational age (GA) and sex were randomly generated and included in the covariate PK dataset.

Third step – Apply population PK model to estimate reference parameters

To evaluate and compare performance of imputation methods, the point estimate Q and the standard error σ of pharmacometric model parameters $V_{\mathrm{pop}}$, ${\mathrm{CL}}_{\mathrm{pop}}$, and ${\beta }_V$ were estimated from the generated reference covariate PK dataset without missing values. To this end, a one‐compartment i.v. population PK model was fitted to the concentration‐time data using nonlinear mixed effects modeling. Estimated model parameters $V_{\mathrm{pop}}$, ${\mathrm{CL}}_{\mathrm{pop}}$, and ${\beta }_V$ served as “ground truth” (also called reference model parameters in the following) for comparison with model parameters estimated with population PK datasets with imputed covariates.

These population PK analyses were performed with the R‐interface package lixoftConnectors ²⁰ for Monolix. ¹⁹

Fourth step – Create reduced population PK datasets with missing covariate information

Missingness was introduced to the covariate PK dataset by removing values in the baseline variable BW. Scenarios with four different proportions of missing covariate data (10%, 20%, 30%, and 40%) were generated. Additionally, scenarios were defined in which the missing values were either within the range of the non‐missing BW values, or they were above the maximal non‐missing BW. Note that the missingness assumption was still MAR because the missingness process was dependent on an observed variable. If this would not be the case, the missingness would be MNAR. It should also be noted that the scenario with 20% missing covariate data was considered to be the core evaluation scenario in this study, albeit this is a rather high level of missingness for a clinical study but possible in retrospective clinical datasets, especially in pediatrics.

The missingness under MCAR and MAR was generated with the ampute function from the mice package. ²¹ Under MCAR, the probability for a BW value to be missing was equally distributed among all samples. Under MAR, the missing probability was calculated based on the logistic function giving a higher missing probability with increasing observed estimate of V. We do not address MNAR missingness in the paper.

Fifth step – Impute missing covariate information with various methods

In an initial step, the i.v. bolus one‐compartment population PK model was fitted without any covariate effect to the PK dataset with all subjects. Individual estimates for V were also utilized during data imputation leveraging available information in the covariate PK dataset. ²² Thus, the following variables were included in each imputation method: BW, BL, GA, sex, and estimated V.

Four established statistical methods and two ML‐based methods to handle missing values were evaluated and compared in this study. The methods can be separated in single and multiple imputation methods (Table 1). Single imputation methods impute the missing values once. Thus, one completed dataset is generated and resulting parameters with this dataset are the final parameter estimates. Multiple imputation methods generate m multiple completed datasets. These datasets are analyzed separately resulting in m sets of parameter estimates. These multiple parameter sets are combined to one single set of parameter estimates according to Rubin's rules (details in the sixth step). In this study, the default value of m = 5 in the R package mice ²¹ was applied.

TABLE 1.

An overview of the six methods to handle missing values and the related separation into single and multiple imputation methods

	LD a	Mean	Norm	PMM	RF	ANN
Single imputation	X	X
Multiple imputation			X	X	X	X

Abbreviations: ANN, artificial neural network; LD, listwise deletion; PMM, predictive mean matching; RF, random forest.

^a Even though LD does not impute the missing values it is listed as single imputation method because only one dataset for the analysis is generated.

In the following section, we introduce each of the evaluated statistical and ML‐based imputation methods. Further information, including small examples and the exact implementation, can be found in Appendix S1.

Four standard statistical imputation methods

LD refers to the deletion of records with at least one missing value (i.e., in this study, a missing BW value), followed by fitting the PK model, with data from patients without any missing values (i.e., using only the complete cases).

Mean imputation simply replaces all missing data in a variable (i.e., BW) by the average of the observed values for this variable.

Norm imputation is implemented as a standard statistical method for continuous variables in the mice package. ²¹ It fits a Bayesian linear regression model to the complete cases (i.e., those following LD) with BW as the dependent variable of the regression. Subsequently, the method randomly samples m parameter sets from the posterior parameter distribution, and then uses each of the respective parameter sets in turn to impute the missing values from the associated linear model, finally generating m multiple imputed complete datasets. ¹²

Predictive mean matching (PMM) imputation is another standard method in the mice package. PMM performs a Bayesian linear regression to calculate the similarity between each data point with a missing value and all complete cases (similar to Norm above). In turn, for each missing value, the method then selects the most similar complete cases as potential donor candidates. The BW from one randomly sampled donor candidate is taken to replace the missing value in one dataset. This procedure is then repeated for the remainder of the missing values in the dataset yielding a single complete dataset. This procedure is then repeated m times, generating m multiple imputed complete datasets.

Two ML‐based imputation methods

RF is based on an assembly of multiple decision trees, ²³ with a stochastic component where, for each individual decision tree, a random subset of data points and variables is sampled. The random choice of samples per decision tree means that RF can be implemented as a multiple imputation approach. ²⁴

ANNs are function approximators mapping input variables to output variables. It has been shown that under some assumptions, ANNs can approximate any function. ²⁵ The parameters in an ANN get calibrated during a training step based on a gradient‐based optimizer. The data for this training step consisted of the complete cases only. Note that ANNs were implemented as a multiple imputation approach as well.

For the Norm and PMM imputations, the mice function of the mice package was utilized. For the RF algorithm, the missForest package was used. ²⁴ For Norm, PMM, and RF, we applied the default settings of the corresponding R packages. The ANN was generated through the torch package. ²⁶ For ANN, an initial network structure was proposed without a full grid search for an optimal architecture or hyperparameter tuning. This was less than optimal, but meant there were comparable implementations using default settings as for the other methods (see Appendix S1 for details on the network structure).

Sixth step – Apply population PK model to re‐estimate model parameters utilizing imputed covariate datasets

The same population PK model was applied to re‐estimate parameters with imputed covariate datasets. For the single imputation methods, the point estimate $\overline{Q}$ and the standard error $\overline{\sigma }$ of the model parameters $V_{\mathrm{pop}}$, ${\mathrm{CL}}_{\mathrm{pop}}$, and ${\beta }_V$ were estimated directly from the single generated complete covariate PK dataset. For the multiple imputation methods, point estimates $\widehat{Q_l}$ and standard errors $\widehat{{\sigma }_l}$ were estimated for each completed dataset, resulting in m sets of estimated model parameters. These sets were combined to single estimates $\overline{Q}$ and $\overline{\sigma }$ according to Rubin's rules ²⁷ such that

$$\overline{Q}=\frac{1}{m}\sum _{l=1}^m\widehat{Q_l}$$

$${\overline{\sigma }}^2=\widehat{W}+\frac{m+1}{m}\widehat{B}$$

where $\widehat{W}$ is the within imputation variance

$$\widehat{W}=\frac{1}{m}\sum _{l=1}^m{\widehat{{\sigma }_l}}^2$$

and $\widehat{B}$ is the between imputation variance

$$\widehat{B}=\frac{1}{m-1}\sum _{l=1}^m{\left(\widehat{Q_l}-\overline{Q}\right)}^2$$

These population PK analyses were also performed with the R‐interface package lixoftConnectors ²⁰ for Monolix. ¹⁹

Seventh step – Assess and compare performance of imputation methods

The procedures presented in the second to sixth steps were repeated 50 times with different reference covariate PK datasets to distinguish between stochastic and systematic errors in the subsequent results. For each repetition, the relative bias between the “ground truth” estimates, Q and σ, and estimates from the missing‐value methods, $\overline{Q}$ and $\overline{\sigma }$, were calculated as follows:

$$\text{Relative}\mathrm{bia}{\mathrm{s}}_Q=\frac{\overline{Q}-Q}{Q}$$

$$\text{Relative}\mathrm{bia}{\mathrm{s}}_{\sigma }=\frac{\overline{\sigma }-\sigma }{\sigma }$$

In addition, the coverage rate ²⁸ (CR) was investigated over all 50 repetitions. Note that because we are interested in the imputation step only, CR was defined as the proportion of confidence intervals that contain the estimated reference parameters from step three ²⁸ , ²⁹ , ³⁰ in contrast to CR when we are interested in the estimation step where the CR calculation is based on the true parameter values. A t‐distribution was assumed for the confidence interval estimation. Note that the following equation was applied to compute the degrees of freedom of the t‐distribution for the multiple imputation methods:

$$v=\left(m-1\right){\left(\frac{\widehat{W}+\left(1+m^{-1}\right)\widehat{B}}{\left(1+m^{-1}\right)\widehat{B}}\right)}^2$$

where $\widehat{W}$ is the within imputation variance, $\widehat{B}$ is the between imputation variance, and m is the number of imputed datasets.

Performance of evaluated imputation methods was assessed with following three criteria: (i) similar point estimates as the reference PK dataset without missing values; hence, the point estimate bias (Bias_σ) should be distributed closely around zero; (ii) increased standard errors due to the increased uncertainty coming from the missing data; hence, standard error biases Bias_σ should be less than zero; and (iii) CR of approximately the same as the nominal confidence interval of 95%, with a lower CR considered a drawback in terms of the performance criteria of the approach. ⁶ , ²⁸ , ²⁹ , ³⁰

RESULTS

In this section, we highlight results from the core evaluation scenario with 20% missing covariate information as a realistic proportion of missing values (e.g., in retrospective studies (Tables 2 and 3)). Results from the scenarios with 10%, 30%, and 40% missing covariate data are summarized in Tables S2 and S3. We begin by presenting the results from scenarios with linear relationships and then go on to those with nonlinear relationships. As mentioned previously, the relationship between the two covariates BW and BL, and that between BW and key PK parameter volume of distribution were investigated. Additionally, the performance of imputation methods with covariate effects of BW on CL are briefly summarized in a later section.

TABLE 2.

The coverage rate of the covariate effect ${\beta }_V$ for the missing data handling methods under different scenarios with 20% missing values in BW

	LD	Mean	Norm	PMM	RF	ANN
Linear
MCAR	100%	100%	100%	100%	100%	100%
MAR	92%	100%	100%	100%	100%	100%
Nonlinear
MCAR	94%	100%	92%	100%	94%	90%
MAR	90%	100%	42%	90%	92%	94%
Outside observed range	100%	94%	90%	50%	30%	64%

Abbreviations: ANN, artificial neural network; ${\beta }_V$, volume of distribution; BW, birth weight; LD, listwise deletion; MAR, missing at random; MCAR, missing completely at random; PMM, predictive mean matching; RF, random forest.

TABLE 3.

The coverage rate of the population estimates for the volume of distribution $V_{\mathrm{pop}}$ for the missing data handling methods under different scenarios with 20% missing values in BW

	LD	Mean	Norm	PMM	RF	ANN
Linear
MCAR	100%	100%	100%	100%	100%	100%
MAR	82%	24%	100%	100%	100%	100%
Nonlinear
MCAR	98%	76%	100%	100%	98%	100%
MAR	98%	2%	84%	98%	92%	90%
Outside observed range	100%	0%	88%	4%	2%	74%

Abbreviations: ANN, artificial neural network; BW, birth weight; LD, listwise deletion; MAR, missing at random; MCAR, missing completely at random; PMM, predictive mean matching; RF, random forest; V _pop, population volume of distribution.

Under linear MCAR assumptions, all classical methods (LD, mean, Norm, and PMM) estimate the model parameters flawlessly with desired CRs (Figure S1). Only the estimated interindividual variability (IIV) for V, ${\omega }_V$, increased with mean imputation. This was also the case for all other investigated scenarios (Figures S2 and S4). This finding is expected as the mean imputed BW values could not explain the variability in V. Together with graphical examinations of the simulated datasets, we considered these results as validation for the process of missing data generation and fitting the PK analysis model. The other scenarios under MCAR assumptions are not discussed in detail here because MCAR assumptions are usually considered unrealistic. ⁶

Performance of imputation methods under linear relationships between BL and BW and between BW and V _pop

Standard statistical imputation methods – For the data in which there is a linear relationship between BL and BW and between BW and $V_{\mathrm{pop}}$, under the MAR assumption for missingness in BW, LD provided a slightly decreased coverage rate of 92% for the covariate effect ${\beta }_V$ compared to the desired 95%. This can also be observed in a skewed bias distribution (Figure 2a). As expected, the population estimates for the volume of distribution $V_{\mathrm{pop}}$ are biased with LD and mean imputation, as shown in Figure 2c, with a coverage rate of 82% and 24%, respectively. The multiple imputation methods Norm and PMM showed unbiased results with coverage rates above 95% for ${\beta }_V$ and $V_{\mathrm{pop}}$.

FIGURE 2.

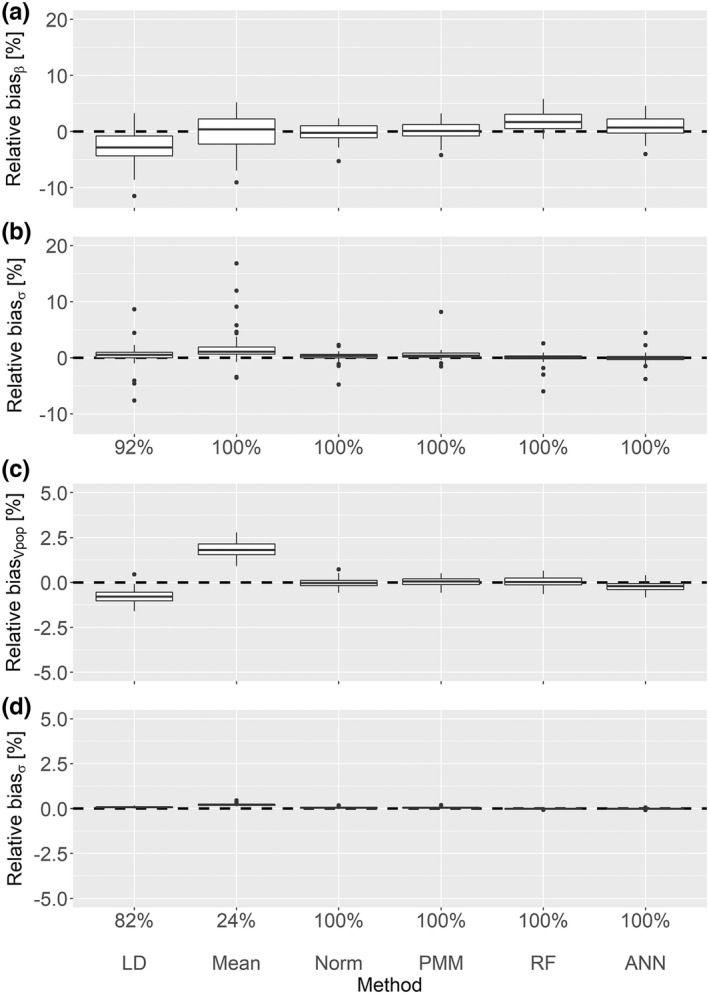
Linear MAR scenario with 20% missing values. This plot shows the relative point estimate and standard error biases for the covariate effect (a, b) and the volume of distribution (c, d) with the corresponding coverage rates. ANN, artificial neural network; LD, listwise deletion; MAR, missing at random; PMM, predictive mean matching; RF, random forest.

ML‐based imputation methods – The ML methods RF and ANN provided coverage rates above 95% for both estimated parameters. However, the standard error biases of the RF and the ANN imputation were very small compared with the multiple imputation methods, as shown in Figures 2b,d.

Performance of imputation methods under nonlinear relationships between BL and BW and between BW and V _pop

Standard statistical imputation methods – For the data in which there is a nonlinear relationship between BL and BW and between BW and $V_{\mathrm{pop}}$ with MAR conditions, LD provided a mildly decreased coverage rate of 90% for ${\beta }_V$ and it was not biased for $V_{\mathrm{pop}}$. In contrast, mean imputation showed strongly biased results for $V_{\mathrm{pop}}$ (Figure 3c) with a decreased coverage rate of only 2%. Even though the covariate effect biases are skewed from a distribution around zero with mean imputation (Figure 3a), strongly increased standard errors (Figure 3b) resulted in a coverage rate above 95%. The multiple imputation method Norm provided biased results for ${\beta }_V$ and $V_{\mathrm{pop}}$ resulting in reduced coverage rates of 42% and 84%, respectively. The method PMM was slightly biased for the covariate effect resulting in a coverage rate of 90%, whereas the coverage rate for $V_{\mathrm{pop}}$ was unbiased.

FIGURE 3.

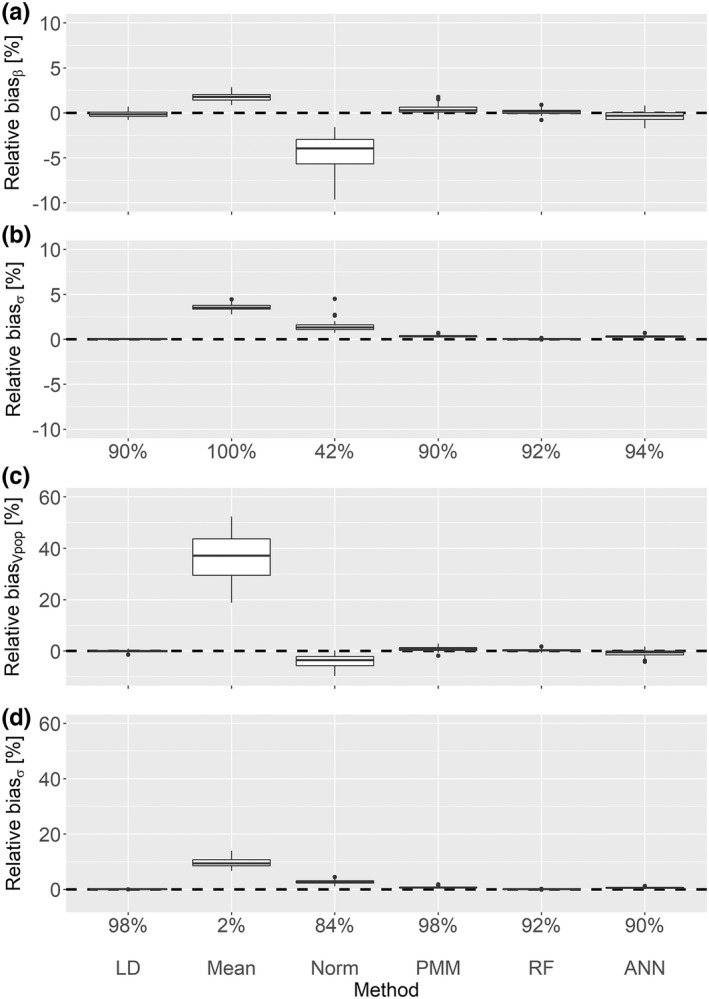
Nonlinear MAR scenario with 20% missing values. This plot shows the relative point estimate and standard error biases for the covariate effect (a, b) and the volume of distribution (c, d) with the corresponding coverage rates. ANN, artificial neural network; LD, listwise deletion; MAR, missing at random; PMM, predictive mean matching; RF, random forest.

ML‐based imputation methods – The coverage rates for RF and ANN were slightly decreased for both volume of distribution (92% and 90%, respectively) and covariate effect (92% and 94%, respectively) compared to the desired 95%.

Performance of imputation methods with missing values outside known covariate range

Standard statistical imputation methods – Assuming a linear relationship between the covariates and under MAR, when the unknown covariate values were not in the observed value range and needed to be extrapolated, all methods except LD had biased estimates (refer to Figure 4a). LD had a coverage rate above 95% for both ${\beta }_V$ and $V_{\mathrm{pop}}$. Mean imputation was strongly biased with a coverage rate of 0% for $V_{\mathrm{pop}}$. Norm imputation provided slightly biased results with coverage rates of 90% and 88% for ${\beta }_V$ and $V_{\mathrm{pop}}$, respectively. PMM was not able to impute values outside of the observed value range, resulting in strongly biased coverage rates of 50% for ${\beta }_V$ and of 2% for $V_{\mathrm{pop}}$.

FIGURE 4.

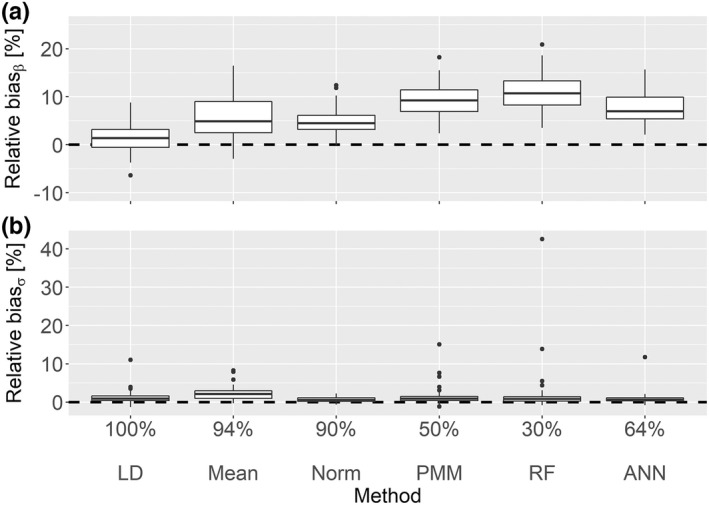
Linear MAR scenario with 20% missingness and missing values outside of observed value range. This box‐plot shows the relative point estimate (a) and standard error (b) biases of the covariate effect on the volume of distribution with the corresponding coverage rates where the missing values are not in the range of the available values. ANN, artificial neural network; LD, listwise deletion; MAR, missing at random; PMM, predictive mean matching; RF, random forest.

ML‐based imputation methods – ANN provided better results with coverage rates of 64% and 74% for ${\beta }_V$ and $V_{\mathrm{pop}}$, respectively. Similar to PMM, RF was not able to impute values outside of the observed value range, resulting in strongly biased coverage rates for ${\beta }_V$ (30%) and for $V_{\mathrm{pop}}$ (2%).

Performance of imputation methods with covariate effects of BW on CL

The evaluated imputation methods delivered structural similar results when there was a covariate effect of BW on CL (Figures S5 and S6) compared with the results when there was a covariate effect of BW on $V$ (Figures 2 and 3).

Stress tests with higher proportions of missing covariate data

In the “stress test,” higher proportions of missing covariate data, such as 30% and 40%, led to similar results, but increasingly extreme results in terms of bias compared to the core evaluation scenario with 20% missing covariate data (refer to Tables S2 and S3).

DISCUSSION

To our knowledge, this is the first simulation study that investigates ML imputation methods in the field of pharmacometrics and compares these to classical methods. We investigated and compared four classical statistics methods and two ML‐based methods to handle missing covariate data in a pharmacometric analysis. This research work contributes to the awareness of such novel ML‐based imputation methods, enhances our understanding where they may benefit pharmacometric projects, and where classical statistical methods may be the preferred choice.

Whereas we focus on results from models with a covariate effect on the volume of distribution, the structural similar results from models with a covariate effect on the CL indicate that our findings are not model parameter‐specific.

Results from the performed analyses confirm previous studies concluding that mean imputation is strongly biased under some scenarios and that LD can result in biased estimates under the MAR assumption. ³¹ , ³² , ³³ This finding is not surprising because both methods may result in biased estimates if the missingness process is not MCAR. Even though LD resulted in rather small relative bias in the evaluated cases, and it may also perform well under MAR assumptions in some scenarios, ⁶ , ³⁴ , ³⁵ the exclusion of samples from the dataset may reduce the statistical power of the analysis. Therefore, both LD and mean imputation require careful considerations concerning the incomplete dataset and should be avoided in cases with increased proportions of missing data, given the availability of other more statistically robust imputation methods. ⁶ , ³⁶ However, LD is often used for the primary analysis in a study to provide a benchmark with which to compare with the multiply imputed results in subsequent supplementary or sensitivity analyses.

Standard statistical imputation methods – Multiple imputation using the Norm method from the mice package only led to unbiased results when the relationships in the data and the imputation model were consistent. As we deliberately did not account for nonlinearity in the multiple imputation model utilizing the Norm method, the results are hardly surprising. Nonetheless, this confirms the necessity to perform exploratory analyses prior to imputation to determine possible nonlinear relationships, and then to proceed accordingly when using this approach. The other multiple imputation method, PMM, provided unbiased results irrespective of the linear or nonlinear covariate relationship. Further, PMM was found to outperform the default settings of all the other investigated imputation methods, with the proviso that imputing missing values outside of the observed value range led to biased results. This succinctly highlights the potential benefits and drawbacks of PMM where the availability of a suitable donor pool of similar patients is key.

ML‐based imputation methods – Results from the ML‐based method RF demonstrates the great potential of this method for imputation tasks. Even though observed biases were slightly increased under some conditions, we should take into consideration that default settings of the R package were used, and only basic data preparation steps were performed. Similar to PMM, RF is limited to imputing values within the observed value range. Optimized implementation of the ML‐based approaches with an adaptation of parameters, such as the number of trees in the RF or the network structure of the ANN, can further improve results. Parameter‐tuning is one of the great advantages of ML‐based approaches. Of the two ML methods, the best results were obtained with ANN. In most scenarios, ANN provided similar coverage rates to PMM. In contrast to PMM and RF, in the scenario with missing values outside of the observed value range, ANN shows some capability to extrapolate values.

We verified that the differences between the results for linear and nonlinear relationships do not arise from the differences in the magnitude of the model parameters by performing an evaluation with accordingly adjusted model parameters in the linear model where similar performance patterns were observed.

A limitation of this simulation study is the number of performed multiple imputations. Even though m = 5 is the default setting in the mice package, currently, a larger number of multiple imputations is usually performed to achieve robust standard error estimation. Because we were investigating various methods in multiple scenarios, including population PK analyses with the R interface to Monolix, more multiple imputations were not feasible due to long run times. Similarly, the number of simulated datasets might be considered low for a simulation study. Nevertheless, the Monte Carlo error was observed to be small compared with observed biases. To reduce complexity, we focused on missing data under the MCAR and MAR assumptions, but acknowledge the importance of methods that investigate plausible MNAR departures from MAR. ⁶ , ⁸ , ³⁷ This is certainly an area for additional research activities. Further, the applied definition of CR differs from the common definition because the previously estimated reference parameters were assumed to be the ground truth in contrast to the true parameters used for simulation. However, this procedure is in accordance with other evaluations focusing on imputation methods. ²⁸ , ²⁹ , ³⁰

This evaluation of imputation methods demonstrates that the application of some conventionally applied imputation methods, such as LD and mean/median imputation require strong assumptions to be made about the missingness process (i.e., MCAR), which are often not thought to be appropriate. Additionally, a deep understanding of the relationships in the dataset is required when applying model‐based imputation methods, such as Norm imputation. We also showed that the ML‐based methods RF and ANN appropriately impute missing covariate data within a pharmacometrics framework, leading to broadly similar results in terms of bias compared with established statistical methods, such as PMM. The ML‐based approaches have increased flexibility concerning nonlinear and interaction relationships compared with the standard approaches, and they provide potential for further enhanced performance through optimized parameter tuning. This feature is particularly relevant for covariate analysis in the pharmacometric field.

AUTHOR CONTRIBUTIONS

D.S.B., U.N., A.A., G.K., and M.P. wrote the manuscript. D.S.B., U.N., A.A., and G.K. designed the research. D.S.B. performed the research. D.S.B., U.N., A.A., and G.K. analyzed the data.

FUNDING INFORMATION

No funding was received for this work.

CONFLICT OF INTEREST

The authors declared no competing interests for this work.

Supporting information

Figure S1

Figure S2

Figure S3

Figure S4

Figure S5

Figure S6

Table S1

Table S2

Table S3

Appendix S1

Appendix S2

Appendix S3

Bräm DS, Nahum U, Atkinson A, Koch G, Pfister M. Evaluation of machine learning methods for covariate data imputation in pharmacometrics. CPT Pharmacometrics Syst Pharmacol. 2022;11:1638‐1648. doi: 10.1002/psp4.12874