Compensating for academic loss: Online learning and student performance during the COVID-19 pandemic

Abstract

The COVID-19 pandemic has led to widespread school shutdowns, with many continuing distance education via online-learning platforms. We here estimate the causal effects of online education on student exam performance using administrative data from Chinese Middle Schools. Taking a difference-in-differences approach, we find that receiving online education during the COVID-19 lockdown improved student academic results by 0.22 of a standard deviation, relative to pupils without learning support from their school. Not all online education was equal: students who were given recorded online lessons from external higher-quality teachers had higher exam scores than those whose lessons were recorded by teachers from their own school. The educational benefits of distance learning were the same for rural and urban students, but the exam performance of students who used a computer for online education was better than those who used a smartphone. Last, while everyone except the very-best students performed better with online learning, it was low achievers who benefited from teacher quality.

1. Introduction

The outbreak of the COVID-19 pandemic has generated unprecedented public-health concerns. Many countries have imposed lockdowns in order to reduce social contact and contain the spread of the Novel Coronavirus (Bonaccorsi et al., 2020; Fang, Wang, & Yang, 2020; Qiu, Chen, & Shi, 2020). As part of lockdowns, the closing of schools has created considerable challenges for teachers, students, and their parents.1 This lost time at school may well have an adverse impact on children's educational outcomes and their future well-being (Aucejo, French, Araya, & Zafar, 2020; Azevedo, Hasan, Goldemberg, Geven, & Iqbal, 2021; Engzell, Frey, & Verhagen, 2021; Eyles, Gibbons, & Montebruno, 2020). To help mitigate the effect of physical closures, many schools have provided online lessons to their students.

We here evaluate the effectiveness of distance delivery of education on student academic outcomes, using administrative data on Ninth Graders from three Chinese Middle Schools in the same county in Baise City. These three schools (which we will call Schools A, B, and C) administered different educational practices over a seven-week period from mid-February to early April 2020 during the COVID-19 lockdown. School A did not provide any online educational support to its students. School B used an online learning platform provided by the local government, which offered a centralized portal for video content, communication between students and teachers, and systems for setting, receiving, and marking student assignments. The students' online lessons were provided by School B's own teachers. School C used the same online platform as School B over the same period, and distance learning was managed by the school in the same fashion as in School B. The only difference between Schools B and C is that, instead of using recorded online lessons from the school's own teachers, School C obtained recorded lessons from the highest-quality teachers in Baise City (these lessons were organized by the Education Board of Baise City). For students in the Ninth Grade, all Middle Schools in the county had finished teaching them all of the material for all subjects during the first five semesters of Middle School (from September 2017 to January 2020). Schools B and C then used online education during the COVID-19 lockdown (from mid-February to early April 2020 in the final (sixth) semester) for the revision of the material that had already been taught, to help Ninth Graders prepare for the city-level High-School entrance exam at the end of the last semester in Middle School. After the COVID-19 restrictions were loosened, all Middle Schools in the county reopened on April 6^th 2020. On April 7^th, Ninth Graders were told that the local Education Board had scheduled exams to take place from April 9^th to the 12^th in each of the subjects that they had been taught in Middle School. The exam in each subject was the same for all Ninth Graders in each of the Middle Schools in the county.

The different educational choices made by the three schools during the COVID-19 crisis offer a natural experiment to identify the causal effects of online education on student academic performance. Our difference-in-differences (DID) estimation reveals that online learning during lockdown improved student performance by 0.22 of a standard deviation, compared to that of students who received no learning support from their school. The quality of the lessons also made a difference: students who had access to online lessons from external best-quality teachers achieved 0.06 standard-deviation better exam results than those whose lessons were recorded by teachers from their own school. The effects of online education were the same for rural and urban students, but were more effective for students who used a computer as their learning device than for those who used a smartphone. We then show that the benefits of the distance learning in Schools B and C were not equally distributed by student quality: quantile DID estimates show that low-achieving students benefited the most from distance learning, with there being no impact for the top academic performers. As such, online delivery of education helped narrow the achievement gap between struggling students and their higher-achieving peers during the COVID-19 lockdown.

We contribute to the literature in three ways. First, there has been little quantitative research on the educational consequences of the COVID-19 pandemic.2 Using survey data from Arizona State University, Aucejo et al. (2020) find negative effects of COVID-19 on university students' outcomes and expectations, including delayed graduation and worse labor-market prospects; they also show that the adverse consequences of COVID-19 were more pronounced for students from disadvantaged backgrounds. In Maldonado and De Witte (2020), Primary-School students in Belgium experienced significant learning losses in standardized tests administered after the COVID-19 school lockdown, as compared to the previous cohort. Engzell et al. (2021) show that students in the Netherlands made little or no progress when learning at home during an eight-week lockdown, with the learning loss being the largest among students from disadvantaged families. Moreover, Bacher-Hicks, Goodman, and Mulhern (2021) use high-frequency internet search data to show that the rise in the demand for online resources is substantially higher in high-SES than in low-SES areas. During lockdowns, remote learning is probably the only way to tackle the disruption in classroom education (Eyles et al., 2020).3 However, there is not yet any empirical evidence on the impact of different types of online education on student performance when schools are physically shut under human-mobility restrictions.4 Using data on students from China's Middle Schools, we here present novel evidence on the causal impact of online education on student academic performance during the COVID-19 crisis, and ask whether some groups of students did better than others.

We second add to the experimental evidence on the effects of instruction models on student performance (Alpert, Couch, & Harmon, 2016; Bettinger, Fox, Loeb, & Taylor, 2017; Bowen, Chingos, Lack, & Nygren, 2014; Cacault, Hildebrand, Laurent-Lucchetti, & Pellizzari, 2021; Figlio, Rush, & Yin, 2013; Kozakowski, 2019). There are two common features in the existing work: the analysis first compares the relative effects of face-to-face, fully online, and blended learning, and second is carried out for post-Secondary education. The calculation of the absolute effects requires information on a fairly rare reference group: students who receive no learning support from an educational institution over the period but take the same exams as the other treated students. Our data here include students from a Middle School who received no learning support from their school during the Chinese school shutdowns, but who took the same exam as the other students immediately after returning to school once the COVID-19 restrictions were released. The comparison of these students to the online-learning students in the other two Middle Schools provides causal evidence on the absolute effects of online education on the exam performance of Middle-School students.5

Last, we provide new evidence on the effect of teacher quality on student achievement. Previous work such as Rivkin, Hanushek, and Kain (2005); Aaronson, Barrow, and Sander (2007); Chetty, Friedman, and Rockoff (2014) and Araujo, Carneiro, Cruz-Aguayo, and Schady (2016) has underlined that better-quality teachers in conventional classrooms improve student outcomes. We extend this literature to online education, and ask whether students who received the online lessons recorded by external higher-quality teachers made more academic progress than did those whose lessons were recorded by their own teachers (with all other aspects of online education being managed identically).

The remainder of the paper is organized as follows. Section 2 describes the background, and Section 3 introduces the data. Section 4 discusses the empirical approach, and Section 5 then presents the estimation results. Last, Section 6 concludes.

2. Education in three Chinese middle schools during the pandemic

Primary and Secondary Education in China takes place successively in three different types of school. At the age of around seven, students enter Primary School. After six years in Primary School they go on to Middle School, where they stay for three years.6 At the end of Middle School, students have the possibility of going on to a High School, based on the results of the last exam in their Ninth Grade. High-School education is prized in China, as opposed to attendance at a vocational school or entry into the job market at age 16, which are the options for students with less-good Ninth-Grade exam results.

We consider the education provided by three Middle Schools located in the same county within Baise City in Guangxi Province.7 The county's administrative area is about 2500 km², with a population of around 370,000 people. Apart from the downtown area, the county administration covers 12 townships composed of over 180 administrative villages. There are 11 Middle Schools in the county: three located in the downtown area and eight in different townships.8 We have access to the administrative records of Ninth-Grade students in the three downtown Middle Schools over the 2019–2020 academic year, which is their final Middle-School year and the last year of their compulsory education. There are 2025 Ninth Graders in these three Middle Schools, accounting for 48.5% of all Grade-Nine students in the county.

In the Chinese education system, there are two semesters per year and two exams per semester (a mid-term and a final exam), with several different subjects being evaluated in each exam period. All Middle Schools in the county are governed by the local Education Board and apply the same curriculum. There are five compulsory subjects (Chinese, Math, English, Politics, and History), which are taught in all three Middle-School years. Students take Geography and Biology only in Grades Seven and Eight, Physics in Grades Eight and Nine, and Chemistry in Grade Nine only. With two exams per semester, and two semesters per year, Middle-School students take a total of 12 exams over their three years. At the end of the last Middle-School semester, Ninth Graders take the city-level High-School entrance exam: this is Middle-School exam 12. The results of this last exam are the most important determinant in the competition for admission to good High Schools in the city. Middle-School teaching for all subjects in the county runs between the start of Grade Seven and the end of the first semester of Grade Nine: for the cohort of Ninth Graders in our data, the start of Grade Seven was in September 2017 and the end of the first semester of Grade Nine was in January 2020. The second semester of Grade Nine, which generally runs between February and June, is used for revision to prepare for the city-level High-School entrance exam, which normally takes place at the end of June.

Due to the COVID-19 pandemic and the consequent school closures, students were not able to return to their schools on the previously-scheduled starting date (February 9^th 2020), although there were no confirmed COVID-19 cases in the county at that time.9 Our data here cover Ninth Graders in the three downtown Middle Schools (Schools A, B, and C), which implemented different educational practices in response to the lockdown.

School A did not make any particular arrangements to support student learning during the COVID-19 school shutdown. It did not require its students to connect to an online platform like the other two schools: students were instead told to study on their own and revise what had been learned in the previous semesters. The school did not take any measures to monitor the students' learning progress, did not prescribe any assignments, and did not distribute any educational resources to students during the lockdown.

School B used a flexible and centralized online learning platform provided by the Education Board of Baise City, which offered a portal for the provision of video content and student–teacher interaction, along with procedures for setting, receiving, and marking assignments. It was mandatory for students to register on this online platform and attend the recorded online lessons prepared by School B's own teachers. The online classes were used to review what had been taught in the previous semesters. Time slots were allocated to different subjects in the morning and afternoon, in the same manner as on a regular school day. Students could watch the online lessons again after class and could ask questions and communicate online with their teachers. Students also had weekly assignments, and the work they submitted was marked and commented on by School B's teachers via the learning platform. Last, the teachers monitored the students' progress and participation.

School C used the same online learning platform as School B, and distance education was managed by the school in the same way as in School B. The only difference was that the recorded lessons on the platform were not delivered by School C's teachers: instead, School C obtained recorded online lessons provided by the Baise City Education Board. After the COVID-19 shutdown, the City organized the recording of online classes for each subject in each grade of Primary- and Middle-School education, and the Education Board selected the highest-quality teachers in Baise City for these recorded lessons (in terms of their qualifications, teaching experience, teaching awards received, and other professional recognition).10 None of the Ninth-Grade teachers selected to provide these lessons that helped students review what they had learnt in the previous semesters were from Schools A, B, or C. All of the other online instructional activities were supplied by School C's teachers, using the same arrangements as in School B.

Schools B and C both reacted quickly to the new mode of distance education after the outbreak of the COVID-19 pandemic, and started online education in mid-February 2020, about one week after the normal starting date of the Spring semester.11 Students spent about seven weeks on distance learning, which ended on April 3^rd. With the loosening of COVID-19 restrictions, all Middle Schools in the county reopened physically on April 6^th. Almost all (98%) of Ninth Graders had returned to school by April 7^th, when they were notified that the local Education Board had scheduled exams (covering the material taught in the previous five semesters) from April 9^th to the 12^th (close to the normal dates for midterm exams in the Spring semester).12 The exam scripts in each subject were the same for the Ninth Graders in all the 11 Middle Schools in the county.

3. Data

We use administrative data from the Education Board of the county on the 2025 Ninth Graders who started Middle-School education in September 2017 in Schools A, B, and C. These students were in the last semester of their Middle-School education in the first half of 2020. The data include information on both student characteristics and their scores in the first 11 exams for all subjects taken in Middle School.13

We here focus on the exam results in the five compulsory subjects (Chinese, Math, English, Politics, and History), which were taught in all of the Middle-School semesters. The students took the first nine exams in the cycle over 2017–2019. The tenth exam, the final exam for the first semester of Grade Nine, took place during January 6^th–10^th 2020, before the first confirmed COVID-19 case in Baise City on January 24^th. The 11^th exam in the Middle-School cycle took place during April 9^th–12^th, after the schools had reopened on April 6^th. These exams are all standardized within the county in terms of the exam questions and the anonymous marking procedure, so that the exam scores can be compared across schools.

We exclude the 190 Ninth Graders who ever (i) changed schools, (ii) missed an exam, or (iii) did not return to school in April 2020. Our final sample consists of 20,185 observations on exam results for the 1835 students who took all of the first 11 exams in the five compulsory subjects. Table 1 shows students' summary statistics in the three schools when they took their first Middle-School exam from November 6^th to the 8^th 2017. School C registered the best academic performance in this first exam, while that in School A was the worst.

Table 1.

Students' characteristics when taking their first Middle-School exam in November 2017.

	Control group		Treatment groups				Mann-Whitney test p-value
	School A		School B		School C
	Mean	S.D.	Mean	S.D.	Mean	S.D.	A = B	A = C
Academic performance
Total score (range: 0–560)	280.9	100.5	326.6	109.8	338.3	102.5	0.00	0.00
Chinese (range: 0–120)	67.4	19.4	78.7	19.4	81.0	16.6	0.00	0.00
Math (range: 0–120)	39.6	27.3	58.7	30.4	64.1	32.5	0.00	0.00
English (range: 0–120)	54.5	24.3	66.9	29.1	67.5	28.9	0.00	0.00
History (range: 0–100)	53.6	22.0	55.0	25.5	59.3	22.7	0.00	0.00
Politics (range: 0–100)	65.9	17.9	67.1	16.3	66.5	13.5	0.00	0.58
Student characteristics:
Age in November 2017	13.1	0.8	12.7	0.8	12.9	0.8	0.00	0.00
Boy	0.44		0.47		0.42		0.29	0.54
Household head is:
Father	0.63		0.71		0.77		0.01	0.00
Mother	0.19		0.11		0.09		0.00	0.00
Neither father nor mother	0.18		0.18		0.14		0.86	0.07
Home-to-school distance (kilometers)	8.8	5.5	9.9	7.1	10.5	7.0	0.18	0.00
Rural student	0.96		0.80		0.89		0.00	0.00
Number of Students	328		871		636

Table 1 also shows some significant differences in student characteristics across schools. It is possible that the three groups also differ in unobservable ways. Therefore, a simple comparison of scholastic performance of the treatment and control groups does not reveal the causal academic impact of online education during the COVID-19 pandemic. In the next section, we introduce the difference-in-differences (DID) framework as our identification strategy. Using DID, we can identify the causal impact of online education on students' learning outcomes, if the treatment and control groups display comparable trends in academic outcomes in the absence of online education.

4. Identification strategy

We carry out a difference-in-differences (DID) estimation to identify the effects of two different types of online education on student academic performance, as follows:

$$Y_{\mathit{ist}}={\mathit{Treatment}}_{\mathit{iB}}\ast {\mathit{Post}}_t\ast {\beta }_B+{\mathit{Treatment}}_{\mathit{iC}}\ast {\mathit{Post}}_t\ast {\beta }_C+X_{\mathit{ist}}\text{'}\gamma +{\mathit{Exam}}_t+{\mu }_i+{\epsilon }_{\mathit{ist}}$$ (1)

where Y _ist is the overall exam score of student i in school s (s=A, B, C) in the t ^th exam (t=1,2, …,11). For ease of interpretation, we standardize the total exam scores from the five compulsory subjects to have zero mean and unit standard deviation. Treatment _iB and Treatment _iC are dummies for the students being from Schools B and C; students in School A are the control group. Post _t is a dummy for the data coming from the 11^th exam in April 2020.14 The X _ist are time-varying control variables, including student age and class-by-school fixed effects. Exam _t are the exam fixed effects, and μ _i the individual fixed effects that control for any differences between the treatment and control groups in student time-invariant characteristics such as innate ability.15 Last, ε _ist is the error term. We cluster standard errors at the student level to account for heteroskedasticity and any arbitrary correlation in exam performance of the same student.

The estimate of β _B reveals the causal impact of the online education adopted in School B on student academic performance, as opposed to School A that stopped providing any support to its students during the COVID-19 crisis. We here identify the impact of the entire package of School B's online education (composed of specific components using the online platform such as recorded online lessons, student–teacher online communications, online assignment marking and feedbacks, etc.) relative to the alternative of no school support during the lockdown.16 Analogously, the comparison of β _C to β _B reveals the comparative effectiveness of the online educational programs of Schools B and C on student learning, which reflects the different quality of teachers who recorded the online lessons (given that all of the other aspects of online education were identical between these two schools).

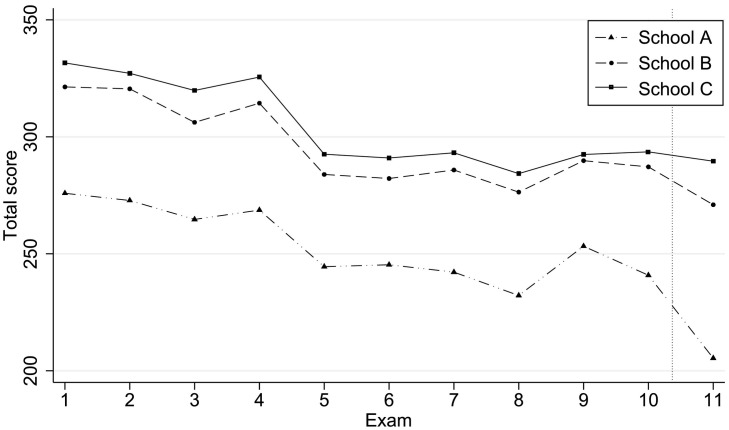
The validity of our DID approach relies on the assumption that, in the absence of the different educational practices in the three schools during the COVID-19 pandemic, the trends in academic outcomes in the treatment and control groups would have remained the same. Fig. 1 shows that students in School C performed slightly academically better than those in school B, while the exam results in School A were notably worse than in the other two schools. In general, the profile of results in these three different schools over the first ten Middle-School exams (i.e. those pre-lockdown) are very similar, providing support to the parallel-trend assumption. It can also be seen that the results for exam 11 (that post-lockdown) are worse than those for exam 10 in all three schools.

Fig. 1.

Parallel trends in pre-lockdown exam scores in Schools A, B and C.

All of the students in our sample come from the same county, and are thus exposed to the same environment: this helps us to identify the causal effects of online learning on student performance. Had the students in the treatment and control groups come from different areas, then the effects of online education on exam results may well have been confounded by the economic and psychological pressures associated with different area-specific COVID-19 outcomes.

5. Results

5.1. Main results

Table 2 shows the results from the DID estimations. In the first column we do not distinguish between the treatments in Schools B and C, and instead ask whether taking part in any kind of online learning (denoted Treatment _iBC) affected overall exam results. The estimated coefficient reveals that online learning during the pandemic led to 0.22 of a standard deviation higher exam grades in the treatment group than in the control group.17 Equivalently, the seven-week online education improved student exam marks by around 26 points (=116∗0.22, where 116 is the standard deviation of the exam-11 marks), relative to those receiving no learning support from their school during the COVID-19 lockdown.18

Table 2.

Online learning and exam results (DID estimates).

	(i)	(ii)
TreatmentiBC ∗ Postt	0.221***
	(0.010)
TreatmentiB ∗ Postt		0.195***
		(0.011)
TreatmentiC ∗ Postt		0.258***
		(0.011)
Test for coefficient equality:
F-statistic	–	47.71
p-value	–	0.00
Individuals	1835	1835
Observations	20,185	20,185
Overall R2	0.109	0.110

Notes: The dependent variable is the standardized total exam score. The control variables include student age, class-by-school fixed effects, exam fixed effects, and individual fixed effects. Standard errors clustered at the individual level appear in parentheses. * p<0.1; ** p<0.05; *** p<0.01.

Column (ii) of Table 2 then distinguishes between the different types of online learning in Schools B and C. The estimated coefficients on both Treatment _iB ∗ Post _t and Treatment _iC ∗ Post _t are positive and statistically significant. However, the F-test at the foot of the table rejects the null hypothesis that these two coefficients are equal. While any online education then improved overall exam performance, that with lessons recorded by higher-quality teachers conferred greater academic benefit. The online learning in School B during lockdown improved student performance by 0.20 of a standard deviation (about 23 exam points), as compared to students who did not receive any learning support in School A. But the quality of the lessons also made a difference: students in School C, who had access to online lessons from external best-quality teachers, recorded an additional 0.06 standard-deviation rise in exam results (about seven exam points) over those whose lessons were recorded by their own teachers in School B. This finding complements previous work underlining that teacher quality translates into student achievement in a conventional classroom-instruction setting (Aaronson et al., 2007; Araujo et al., 2016; Chetty et al., 2014).

5.2. Heterogeneity analysis

Table 2 sets out the average academic impact of online learning over the whole sample. In this section, we explore potential heterogeneity in the estimated effect. Given that the academic effects of distance learning differ by teacher quality (as indicated in Table 2), we will present estimated coefficients for Treatment _iB ∗ Post _t and Treatment _iC ∗ Post _t separately.

5.2.1. Heterogeneous effects of online education across student groups

We consider whether the academic impact of online education differs by student (i) gender, (ii) household type (rural vs. urban), and (iii) the type of electronic device used for online learning (computer vs. smartphone). The resulting difference-in-difference-in-differences (DDD) estimates appear in Table 3 .

Table 3.

Heterogeneous effects of online education by student characteristics (DDD estimates).

	(i) Gender	(ii) Household type	(iii) Device for learning
	Groupi=1 if boy	Groupi=1 if rural	Groupi=1 if smartphone
TreatmentiB ∗ Postt	0.202***	0.191***	0.332***
	(0.014)	(0.057)	(0.028)
TreatmentiB ∗ Postt ∗ Groupi	−0.017	0.005	−0.144***
	(0.021)	(0.058)	(0.030)
TreatmentiC ∗ Postt	0.285***	0.271***	0.398***
	(0.014)	(0.059)	(0.031)
TreatmentiC ∗ Postt ∗ Groupi	−0.065***	0.014	−0.147***
	(0.022)	(0.060)	(0.033)
Individuals	1835	1835	1835
Observations	20,185	20,185	20,185
Overall R2	0.110	0.109	0.110

Notes: The dependent variable is the standardized total exam score. The control variables include student age, class-by-school fixed effects, exam fixed effects, individual fixed effects, and all pairwise interactions between Treatment_is, Post_t, and Group_i. Standard errors clustered at the individual level appear in parentheses. * p<0.1; ** p<0.05; *** p<0.01.

Probably the most common type of online learning is that which was used in School B (all aspects of online education were managed by teachers in own school), and in column (i) of Table 3, Treatment _iB produces the same educational benefits for boys and girls. School C on the contrary used recorded lessons that were designed and delivered by external higher-quality teachers, with no difference in any other aspect of online instruction. In column (i), it can be seen that girls benefited more from Treatment _iC than did boys. In online education during the lockdown, time slots were allocated to different subjects in the morning and afternoon. Students needed to sit in front of their online-learning device for the same number of hours as on a regular school day. Without any teacher being physically present in the same room, the effectiveness of online learning depends critically on students' non-cognitive traits such as self-discipline, agreeableness (one sub-trait of which is cooperation), and conscientiousness. Previous work has found that girls outperform boys in these aspects (Duckworth & Seligman, 2006; Rubinstein, 2005). On the contrary, in column (ii) of Table 3 there is no significant difference in the effects of the two types of online lessons between rural and urban students.

We last ask whether the effects of online learning differed by the type of electronic device.19 In column (iii) of Table 3, while both online-learning models improved student exam performance, students with access to a computer at home benefited 60–75% more than those using a smartphone. Online-class participation is likely easier via computer (Frenette, Frank, & Deng, 2020; Nurhudatiana, Hiu, & Ce, 2018). When students spend long periods in online classes, the screen size of a smartphone can be a distinct disadvantage when compared to that of a computer. It is also easier to profit from recorded lessons while having the relevant course material open on the same screen; this is more difficult to manage on the considerably smaller screen of a smartphone. Last, as smartphones have limited storage space, downloading course documents and submitting assignments pose their own set of challenges. These differences in learning devices may lie behind the heterogeneous effects of online learning during lockdown.

5.2.2. The effect of online education along the student-performance distribution

We next consider whether the educational effects of online learning vary by the student's initial academic performance. We apply the unconditional quantile regression (UQR) of Firpo, Fortin, and Lemieux (2009) to estimate quantile DID regressions. One key element of the UQR approach is the concept of the influence function in robust statistics, representing the impact of one individual observation on a distributional measure (quantile or variance, for example). Adding the influence function back to the distributional measure produces the recentered influence function. If Y _ist is the academic outcome of student i in school s in exam t, the influence function IF(Y _ist, q _τ) for the τ-th quantile of Y _ist is then (τ − I(Y _ist ≤ q _τ))/f _Yist(q _τ), where q _τ is the τ-th quantile of Y _ist, I an indicator function and f _Yist the density of the marginal distribution of Y _ist. The recentered influence function RIF(Y _ist, q _τ) is then q _τ + IF(Y _ist, q _τ), with the theoretical property that its expected value equals q _τ.

As RIF(Y _ist, q _τ) is never observed in practice, we follow Firpo et al. (2009) and replace the unknown components by their sample estimators:

$$\widehat{\mathit{RIF}}\left(Y_{\mathit{ist}},{\widehat{q}}_{\tau }\right)={\widehat{q}}_{\tau }+\frac{\tau -I\left(Y_{\mathit{ist}}\le {\widehat{q}}_{\tau }\right)}{{\widehat{f}}_{Y_{\mathit{ist}}}\left({\widehat{q}}_{\tau }\right)},$$ (2)

where ${\widehat{q}}_{\tau }$ is estimated as arg $\underset{q}{min}{\sum }_{i=1}^N$(τ–I(Y _ist ≤ q))(Y _ist–q). The nonparametric Rosenblatt kernel density estimator ${\widehat{f}}_{Y_{\mathit{ist}}}\left({\widehat{q}}_{\tau }\right)$ is $\frac{1}{N}{\sum }_{i=1}^N\frac{1}{h_Y}{K}_Y\left(\frac{Y_{\mathit{ist}}-{\widehat{q}}_{\tau }}{h_Y}\right)$, where K _Y is the Gaussian kernel and h _Y the scalar bandwidth for Y _ist.

We then model $\widehat{\mathit{RIF}}\left(Y_{\mathit{ist}},{\widehat{q}}_{\tau }\right)$ as a function of the same control variables as in Eq. (1):

$$\widehat{\mathit{RIF}}\left(Y_{\mathit{ist}},{\widehat{q}}_{\tau }\right)={\mathit{Treatment}}_{\mathit{iB}}\ast {\mathit{Post}}_t\ast {\beta }_{\mathit{B\tau }}+{\mathit{Treatment}}_{\mathit{iC}}\ast {\mathit{Post}}_t\ast {\beta }_{\mathit{C\tau }}+X_{\mathit{ist}}^{\prime }{\gamma }_{\tau }+{\mathit{Exam}}_t+{\mu }_i+{\epsilon }_{\mathit{ist\tau }}.$$ (3)

The quantile DID estimates of β _Bτ and β _Cτ from Eq. (3) represent the causal effects of distance education in Schools B and C on the unconditional τ-th quantile of Y _ist in our data.20 Standard errors clustered at the individual level come from bootstrapping with 300 replications. The quantile DID estimates provide a more complete description of the relationship between online learning and the full distribution of academic outcomes.

Table 4 lists the quantile DID estimates at the 10^th to 90^th percentiles of the unconditional distribution of student exam performance. It is clear that the academic effect of online learning is not the same over the student exam-score distribution. The estimated coefficients on Treatment _iB ∗ Post _t and Treatment _iC ∗ Post _t at the lower end of distribution are much larger than those at the top. For example, the positive academic impact of School B's online education at the 20^th percentile is over three times as large as that at the 80^th percentile. Low performers thus benefited the most from online learning programs. We also find that the top academic performers at the 90^th percentile were not affected by online education: these students did well independently of the educational practices their schools employed during lockdown. Outside of these top academic performers, the online learning programs in Schools B and C improved student exam performance.

Table 4.

The heterogeneous effects of online education over the student-performance distribution (Quantile DID estimates).

	Q10	Q20	Q30	Q40	Q50	Q60	Q70	Q80	Q90
TreatmentiB ∗ Postt	0.319***	0.371***	0.316***	0.214***	0.191***	0.188**	0.155***	0.106*	−0.059
	(0.079)	(0.062)	(0.055)	(0.058)	(0.057)	(0.076)	(0.063)	(0.057)	(0.047)
TreatmentiC ∗ Postt	0.486***	0.452***	0.354***	0.263***	0.227***	0.247***	0.192***	0.160***	0.045
	(0.076)	(0.063)	(0.055)	(0.061)	(0.059)	(0.077)	(0.060)	(0.054)	(0.046)
Test for coefficient equality:
F-statistic	16.16	4.73	1.02	1.92	0.52	2.33	0.83	1.60	8.69
p-value	0.00	0.03	0.31	0.17	0.47	0.13	0.36	0.21	0.00
Individuals	1835	1835	1835	1835	1835	1835	1835	1835	1835
Observations	20,185	20,185	20,185	20,185	20,185	20,185	20,185	20,185	20,185
Overall R2	0.033	0.092	0.074	0.048	0.026	0.031	0.006	0.000	0.000

Notes: The dependent variable is the recentered influence function for the τ-th quantile of the standardized total exam score. The control variables include student age, class-by-school fixed effects, exam fixed effects, and individual fixed effects. Bootstrapped standard errors clustered at the individual level appear in parentheses. The quantile DID estimates are calculated using the Stata code xtrifreg by Borgen (2016). * p<0.1; ** p<0.05; *** p<0.01.

Table 2 showed that the average impact of Treatment _iC is larger than that of Treatment _iB; Table 4 underlines that this gap mainly comes from the low achievers at the 10^th and 20^th percentiles. Although the estimated coefficients on Treatment _iC ∗ Post _t are consistently larger than those on Treatment _iB ∗ Post _t, from the 30^th to the 80^th percentile of the academic-performance distribution, the gap is not significant at conventional statistical levels. Instruction thus improves the exam performance of all bar the very-best students, while the quality of this instruction differentially benefits the students with the worst past exam results. In Aaronson et al. (2007), higher-quality teachers in the classroom raise student test scores, and more so for students at the lower end of the initial ability distribution. We here uncover an analogous impact of lessons recorded by higher-quality external teachers on low-achievers, even though these external teachers had no interaction with the students in School C. As such, it is the quality of the material that matters here, independently of any student–teacher interaction.

5.3. Robustness checks

5.3.1. Re-checking the common-trend assumption

DID estimation requires that the trends in the outcomes pre-treatment be similar, and we carry out a number of checks in this section. While Fig. 1 is generally supportive of common trends, there appears to be a slight divergence in exam 10. We first follow Boes, Marti, and Maclean (2015) and calculate separate trends by school in exams 1–10. Specifically, we compute the first-differenced total scores in the first ten exams for each student in the three schools, and then use the t test to check the differences between the control group (School A) and the treatment groups (Schools B and C). These are not significantly different between the treatment and control groups at the 10% level (p-value = 0.76 for Schools A and B; and p-value = 0.11 for Schools A and C).

Second, to formally check whether our results are unduly affected by exam 10, we successively re-estimate the DID regression using only exams t (t=2,3, …,9) to 10 in the pre-treatment period (thus putting increasing weight on exam 10). The results are reported in Table 5 . Our conclusions regarding the exam performance in the three schools hold in each of these estimations. Therefore, the slight divergence in scores in exams 9–10 has little influence on our main results.

Table 5.

Using only exams t (t=2,3, …,9) to 11 for estimation (DID estimates).

	Exams	Exams	Exams	Exams	Exams	Exams	Exams	Exams
	2–11	3–11	4–11	5–11	6–11	7–11	8–11	9–11
TreatmentiB ∗ Postt	0.198***	0.205***	0.208***	0.216***	0.212***	0.202***	0.204***	0.212***
	(0.010)	(0.010)	(0.009)	(0.008)	(0.008)	(0.008)	(0.008)	(0.011)
TreatmentiC ∗ Postt	0.265***	0.267***	0.277***	0.288***	0.290***	0.290***	0.303***	0.329***
	(0.011)	(0.010)	(0.010)	(0.009)	(0.009)	(0.009)	(0.008)	(0.011)
Test for coefficient equality:
F-statistic	63.98	68.90	105.98	185.02	304.49	597.25	1955.96	522.64
p-value	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
Individuals	1835	1835	1835	1835	1835	1835	1835	1835
Observations	18,350	16,515	14,680	12,845	11,010	9175	7340	5505
Overall R2	0.110	0.089	0.096	0.129	0.119	0.091	0.103	0.094

Notes: The dependent variable is the standardized total exam score. The control variables include student age, class-by-school fixed effects, exam fixed effects, and individual fixed effects. Standard errors clustered at the individual level appear in parentheses. * p<0.1; ** p<0.05; *** p<0.01.

Third, we ask whether the three exam-11 results in Fig. 1 are just the continuations of the trends in exams 9 and 10. We create pseudo exam-11 results by correcting for the exam 9–10 trend (this shifts the exam-11 result in School A upwards, as there was already a downward trend pre-lockdown): the results are listed in Table 6 . With these pseudo exam-11 results we continue to find that online learning improves exam results, and more so with higher-quality teachers.

Table 6.

Correcting exam-11 results for the exam 9–10 trend (DID estimates).

	(i)	(ii)
TreatmentiBC ∗ Postt	0.151***
	(0.020)
TreatmentiB ∗ Postt		0.133***
		(0.021)
TreatmentiC ∗ Postt		0.177***
		(0.021)
Test for coefficient equality:
F-statistic	–	9.81
p-value	–	0.00
Individuals	1835	1835
Observations	20,185	20,185
Overall R2	0.179	0.178

Notes: The dependent variable is the standardized total exam score with the exam-11 results being corrected for the exam 9–10 trend. The control variables include student age, class-by-school fixed effects, exam fixed effects, and individual fixed effects. Standard errors clustered at the individual level appear in parentheses. * p<0.1; ** p<0.05; *** p<0.01.

Fourth, we conduct a placebo test using student records in the first ten exams. We assume that online education in Schools B and C took place between the 9th and the 10th exams. As such, the exam-10 results are assumed to be the pseudo post-treatment outcomes. We generate a dummy, Post _t ^p, to indicate the pseudo time of online education between the 9th and the 10th exams. The results in Table 7 show that the estimated coefficients on both Treatment _iB ∗ Post _t ^p and Treatment _iC ∗ Post _t ^p are insignificant. The coefficients are also considerably smaller in size than those in Table 2.

Table 7.

Using exam-10 results as the outcomes in a placebo treatment (DID estimates).

	(i)	(ii)
TreatmentiBC ∗ Posttp	−0.010
	(0.040)
TreatmentiB ∗ Posttp		0.011
		(0.042)
TreatmentiC ∗ Posttp		−0.039
		(0.041)
Test for coefficient equality:
F-statistic	–	5.02
p-value	–	0.03
Individuals	1835	1835
Observations	18,350	18,350
Overall R2	0.179	0.180

Notes: The dependent variable is the standardized total exam score in the first 10 exams. The control variables include student age, class-by-school fixed effects, exam fixed effects, and individual fixed effects. Standard errors clustered at the individual level appear in parentheses. * p<0.1; ** p<0.05; *** p<0.01.

Last, we take a combined propensity score matching and difference-in-differences approach (PSM–DID) to adjust for observed student differences and deal with unobserved confounders that are constant over time across schools. Since the PSM–DID approach allows us to estimate the impact of only one treatment at a time, we carry out this estimation first with data from Schools A and B, and then Schools A and C. To see whether these separate regressions affect the estimated coefficients, Panel A of Table 8 lists the baseline DID results for Schools B and C from two separate regressions (as opposed to the one DID regression in Table 2). The results are reassuring, in that they are almost identical to those in column (ii) of Table 2. In the PSM–DID approach, we use a probit model to estimate the propensity score of being in the treatment group for each student (denoted by $\widehat{p}\left(X_i\right)$), using the observed characteristics in Table 1 as covariates. We then follow Hirano, Imbens, and Ridder (2003) and generate weights of $\frac{1}{\widehat{p}\left(X_i\right)}$ for students in the treatment group and $\frac{1}{1-\widehat{p}\left(X_i\right)}$ for those in the control group. Focusing on the students who are in the treatment and control groups with common support, we carry out DID estimation with these weights to obtain the PSM–DID estimates: these appear in Panel B of Table 8. Only few students are dropped due to a lack of common support, which is not unexpected as the student characteristics in Table 1 are reasonably similar across schools. The weighted DID estimates from the students with common support are very similar to those in Panel A. We also follow Crump, Hotz, Imbens, and Mitnik (2009), and carry out weighted DID estimation on a sample that is further restricted to have estimated propensity scores between 0.10 and 0.90: the results in Panel C remain similar. We conclude that our main findings of the impact of online education on student performance remain robust in estimation samples of students in the treatment and control groups who have comparable observed characteristics.

Table 8.

PSM–DID estimates.

	Panel A: DID estimates		Panel B: PSM–DID estimates $\widehat{p}\left(X_i\right)$ in common support		Panel C: PSM–DID estimates 0.10$\le \widehat{p}\left(X_i\right)\le$0.90
	(i)	(ii)	(iii)	(iv)	(v)	(vi)
TreatmentiB ∗ Postt	0.194***		0.193***		0.207***
	(0.011)		(0.016)		(0.012)
TreatmentiC ∗ Postt		0.258***		0.253***		0.257***
		(0.011)		(0.014)		(0.012)
Individuals	1199	964	1190	951	990	909
Observations	13,189	10,604	13,090	10,461	10,890	9999
Overall R2	0.196	0.132	0.147	0.123	0.155	0.127

Notes: The dependent variable is the standardized total exam score. The control variables include student age, class-by-school fixed effects, exam fixed effects, and individual fixed effects. Standard errors clustered at the individual level appear in parentheses. * p<0.1; ** p<0.05; *** p<0.01.

5.3.2. Assessing the potential confounding impact of time-varying unobservables

The validity of our DID estimates can still be challenged by potential time-varying unobserved factors during the COVID-19 crisis. For example, as Schools B and C provided online lessons during the lockdown, while School A did not, and with the critical High-School entrance exam taking place in a few months, parents of Ninth Graders in School A might have spent comparatively more time monitoring their children's learning progress and/or providing other resources for their children's learning. In this case, we will underestimate the positive effects of online learning on student performance. Schools can also differentially affect student learning via channels other than online education during the lockdown (Angrist, Bergman, & Matsheng, 2021). Teachers in School B may have communicated with parents via SMS messages and/or phone calls, for instance, allowing parents to provide their children with more effective learning support at home, while School-C teachers did not: here we will under-estimate the beneficial impact of teacher quality in recorded online lessons.

It is natural to ask how potential confounding unobservables affect the baseline DID estimates in Eq. (1). If accounting for unobserved factors produces substantially-different results from those in Table 1, we can conclude that our identification strategy is flawed; on the contrary, if the estimates are of similar magnitude, then selection on unobservables is not a major concern.

In this section, we assess the impact of time-varying unobserved factors that are potential correlates of Treatment _iB ∗ Post _t and Treatment _iC ∗ Post _t in Eq. (1).21 As these are unobserved, we cannot control for them directly. We instead turn to the bounding approach, which can partially identify the impact under examination by establishing consistent bounds on the true value that would result had we controlled for all relevant control variables (observed and/or unobserved). The potential bias from omitted control variables can be evaluated by exploring the sensitivity of the estimated coefficients to the inclusion of different observed covariates. Coefficients that remain stable after the inclusion of observed controls can be interpreted as exhibiting limited omitted-variable bias (Altonji, Elder, & Taber, 2005). It should be emphasized that estimated coefficients may also remain stable when the new covariates are uninformative: as such, Oster (2019) suggests also taking into account the explanatory power of the control variables (as measured by the R ² value).

We here use the method in Oster (2019), which adds the R ² value to that of Altonji et al. (2005). We require two key pieces of information to construct the bound estimates. The first is the value of δ that measures the relative degree of selection on observed and unobserved variables. Oster (2019) suggests assuming that the selection on observables is the same as that on unobservables (δ=1). The second is the R ² from a hypothetical regression of the dependent variable on the treatment variable and a full list of observed and unobserved controls (denoted by R _Max ²). Oster (2019) suggests that R _Max ² be set equal to $\mathit{Min}\left\{\mathrm{1,1.3}{\widehat{R}}^2\right\}$, where ${\widehat{R}}^2$ comes from the baseline regression controlling for observed explanatory variables.22 The identified set (or bounds) $[\widehat{\beta }$, β ^∗(R _Max ², δ=1)] includes the true estimate. Here, β ^∗ is estimated as $\widehat{\beta }-\left(\beta -\widehat{\beta }\right)\frac{R_{\mathit{Max}}^2-{\widehat{R}}^2}{{\widehat{R}}^2-R^2}$, where β and R ² are obtained from the regression of the dependent variable on the treatment variable with no controls, and $\widehat{\beta }$ and ${\widehat{R}}^2$ are from the baseline regression with controls. If the identified set $[\widehat{\beta }$, β ^∗(R _Max ², δ=1)] excludes zero, then we can conclude that the true effect of a treatment is not zero and that the baseline estimate $\widehat{\beta }$ is robust to potential selection on unobservables.

The bounding results appear in Table 9 . Panel A presents the controlled-effect estimates (denoted by $\widehat{\beta }$), which are reproduced from column (ii) of Table 1. The identified sets (bound estimates) then appear in Panel B. When R _Max ²=$\mathit{Min}\left\{\mathrm{1,1.3}{\widehat{R}}^2\right\}$ and δ=1, neither of the two identified bounds include zero, and we conclude that the baseline DID estimates are robust to the potential influence of unobservables. Besides establishing whether the bounds include zero, we can also consider the width of the bound estimates. In Treatment _iB ∗ Post _t, the estimated 0.195 standard-deviation increase in student academic performance in School B is robust, but the bound is slightly larger at 0.259. Potential selection on unobservables then produces a bound of the causal pathway between online learning and exam performance in School B at least as large as that in Table 2. The same pattern holds for Treatment _iC ∗ Post _t.

Table 9.

Bound estimates.

	TreatmentiB ∗ Postt	TreatmentiC ∗ Postt
Panel A: Controlled effect $\left(\widehat{\beta }\right)$	0.195*** (0.011)	0.258*** (0.011)
Panel B: Identified set:
$[\widehat{\beta }$, β∗(RMax2, δ=1.0)]	[0.195*** (0.011), 0.259*** (0.016)]	[0.258*** (0.011), 0.299*** (0.014)]
$[\widehat{\beta }$, β∗(RMax2, δ=1.5)]	[0.195*** (0.011), 0.299*** (0.019)]	[0.258*** (0.011), 0.322*** (0.017)]
$[\widehat{\beta }$, β∗(RMax2, δ=2.0)]	[0.195*** (0.011), 0.345*** (0.023)]	[0.258*** (0.011), 0.358*** (0.018)]

Notes: The dependent variable is the standardized total exam score. The results in Panel A are from column (ii) of Table 1. The results in Panel B are calculated using the Stata code psacalc by Oster (2019). Standard errors of β^∗(R_Max², δ) clustered at the individual level are obtained via bootstrapping. * p<0.1; ** p<0.05; *** p<0.01.

It may be that the assumption of the equal importance of the observed and unobserved variables is too strong, and selection on the latter may be greater. We investigate by increasing the value of δ to first 1.5 and then 2.0 in the last two rows of Table 9. This produces increasingly large upper bounds, supporting our conclusion that online education improved student performance during the lockdown.

5.3.3. Using an alternative index of academic performance

The correlation coefficient between the exam results for any two of the five subjects ranges from 0.70 to 0.77 in our data. We thus construct a summary index that takes these substantial correlations into account, using principal component analysis (PCA) to transform correlated exam results into a smaller number of uncorrelated principal components. Applying the Kaiser criterion, we retain the one PCA component with an eigenvalue greater than one, which explains about 79% of the variation in academic outcomes. We then standardize this PCA index so that it has zero mean and unit standard deviation.

Table 10 lists the estimates from the same DID regressions as in Table 2 using this alternative index of scholastic achievement: the results are very similar.23 Our conclusion then remains unchanged: both types of online education improved student exam performance, and online lessons recorded by higher-quality teachers conferred greater academic benefit.

Table 10.

Results with a PCA index (DID estimates).

	(i)	(ii)
TreatmentiBC ∗ Postt	0.247***
	(0.010)
TreatmentiB ∗ Postt		0.217***
		(0.011)
TreatmentiC ∗ Postt		0.288***
		(0.012)
Test for coefficient equality:
F-statistic	–	58.22
p-value	–	0.00
Individuals	1835	1835
Observations	20,185	20,185
Overall R2	0.177	0.179

Notes: The dependent variable is the standardized PCA index of academic performance. The control variables include student age, class-by-school fixed effects, exam fixed effects, and individual fixed effects. Standard errors clustered at the individual level appear in parentheses. * p<0.1; ** p<0.05; *** p<0.01.

6. Conclusion

The COVID-19 pandemic and associated policy responses have generated profound changes in almost every aspect of our social and economic lives. Lockdown measures and social distancing-orders have been introduced by governments to restrict human mobility and limit the spread of disease. To mitigate the learning losses from the significant disruption of education provision during the COVID-19 crisis, many schools switched from physical classroom learning to the distance delivery of education via online platforms.

In this paper, we examined the causal effects of online education on student academic performance, when face-to-face education was prohibited under human-mobility restrictions, using administrative data from Middle Schools in China that introduced different educational practices for around seven weeks during the COVID-19 lockdown. Our DID estimates reveal that online learning, as opposed to no learning support, had a large positive effect on students' overall subsequent exam performance. But the content of the (recorded) lessons also mattered: those recorded by higher-quality teachers produced better exam results. Moreover, while the academic benefits of online learning were the same for rural and urban students, students who engaged in online learning with a computer profited more than those who used a smartphone. Furthermore, quantile DID analysis showed that while any online learning benefited all students outside of the top performers, it was the academically-weaker students who benefited the most from online education and were more reactive to the quality of the teachers providing the online lessons.

Our findings have important policy implications for educational practices when face-to-face education is not possible. First, online learning resources are beneficial for students, and reduce inequality in exam performance (as compared to no academic involvement) as students with worse exam results benefit more. Second, the quality of the teachers who design and deliver the recorded online lessons has a significant effect on students' exam scores. Local governments or education boards can recruit top-quality teachers to prepare online lessons that comply with the local curriculum standards and make these available to schools and students. This is cost-effective, as it comes with substantial economies of scale, and produces better academic outcomes than each school preparing its own online lessons. Last, resources matter: it should be ensured that all students have the resources necessary to access online education (Frenette et al., 2020), potentially through collaboration with the telecommunications sector. If available resources are constrained, priority should be given to low-achieving children as they benefit the most from distance learning.

A number of caveats apply to our findings. First, our data on student academic records and online educational practices comes from only three Middle Schools in one Chinese county. The external validity of our empirical results obviously requires investigation.24 The nationwide evaluation of online learning has not been possible due to data availability. In addition, area-specific COVID-19 conditions may have affected the educational practices that could be adopted by Chinese schools during the crisis. Had our treatment and control groups come from different areas, the effects of online education on exam results could have been confounded by economic and psychological pressure associated with area-specific COVID-19 outcomes. However, all of our students here come from urban schools in the same county, and were thus exposed to the same environment. Our analysis does thus have greater internal validity, but at the cost of lower external validity. Second, we have only looked at the effects of online education used by schools to review material that had already been taught in previous semesters. We would also like to know how effective online education is for the learning of new knowledge. One major challenge here is that the absolute effects of online education (versus the alternative of no learning support from schools) cannot be causally identified as there is no suitable control group: no Chinese school would require students to take an exam covering material that was not taught by their teachers in school. Last, it would also be of interest to examine the relative effects of face-to-face and online education on student performance, as in previous work. This comparison is currently not possible, as face-to-face teaching was prohibited by the Chinese Ministry of Education during the COVID-19 crisis. Equally, under normal circumstances, teaching in Chinese schools is only face-to-face, with no online sessions running in parallel. We leave these aspects for future research when suitable data become available.

Declaration of Competing Interest

None.