FIG. 4.

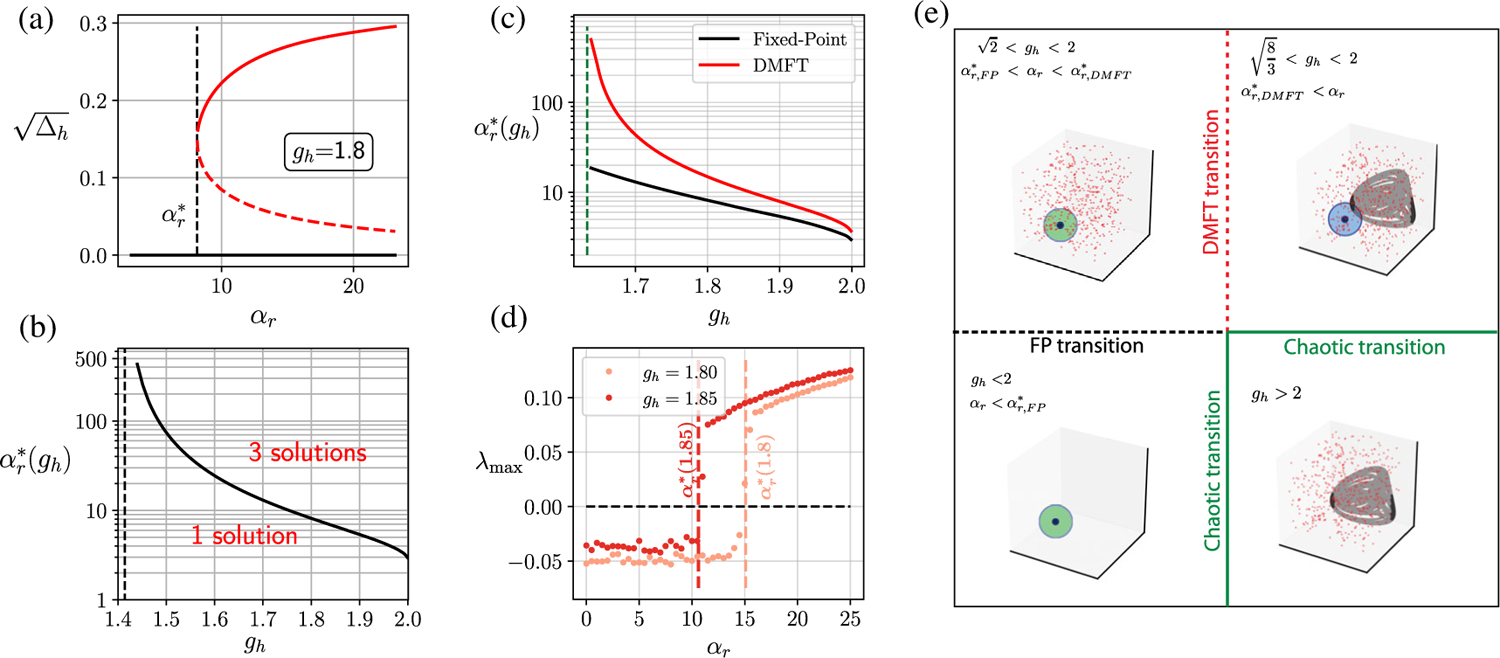
The discontinuous dynamical transition. (a) Spontaneous appearance of nonzero solutions (dashed and solid red lines) to the FP equations once α_r crosses a critical value ${\alpha }_{r,\text{FP}}^{*}\left(g_h\right)$ at fixed g_h. (b) The critical ${\alpha }_{r,\text{FP}}^{*}\left(g_h\right)$ as a function of g_h. The vertical dashed line represents left critical value $g_c=\sqrt{2}$, below which a bifurcation is not possible. (c) The critical DMFT transition curve ${\alpha }_{r,\text{DMFT}}^{*}\left(g_h\right)$ (red curve) calculated using Eqs. (G8) and (G9). The FP transition curve from (b) is shown in black. The green dashed line corresponds to $g_c=\sqrt{8/3}$, below which the dynamical transition is not possible. (d) Numerically calculated maximum Lyapunov exponent λ_max as a function of α_r for two different values of g_h. The dashed lines correspond to the DMFT prediction for the discontinuous transition from (c). (e) Schematic of the bifurcation transition: For g_h < 2 and ${\alpha }_r<{\alpha }_{r,\text{FP}}^{*}$, the zero FP is the only (stable) solution (bottom left box); for $\sqrt{2}<g_h<2$ and ${\alpha }_{r,\text{FP}}^{*}<{\alpha }_r<{\alpha }_{r,\text{DMFT}}^{*}$, the zero FP is still stable, but there is a proliferation of unstable FPs without any obvious dynamical signature (top left); for $\sqrt{8/3}<g_h<2$ and ${\alpha }_r>{\alpha }_{r,\text{DMFT}}^{*}$, chaotic dynamics coexist with the stable FP and this transition is discontinuous (top right); finally, for g_h > 2.0, the stable FP becomes unstable, and only the chaotic attractor remains; this transition is continuous (bottom right).