FIG. 7.

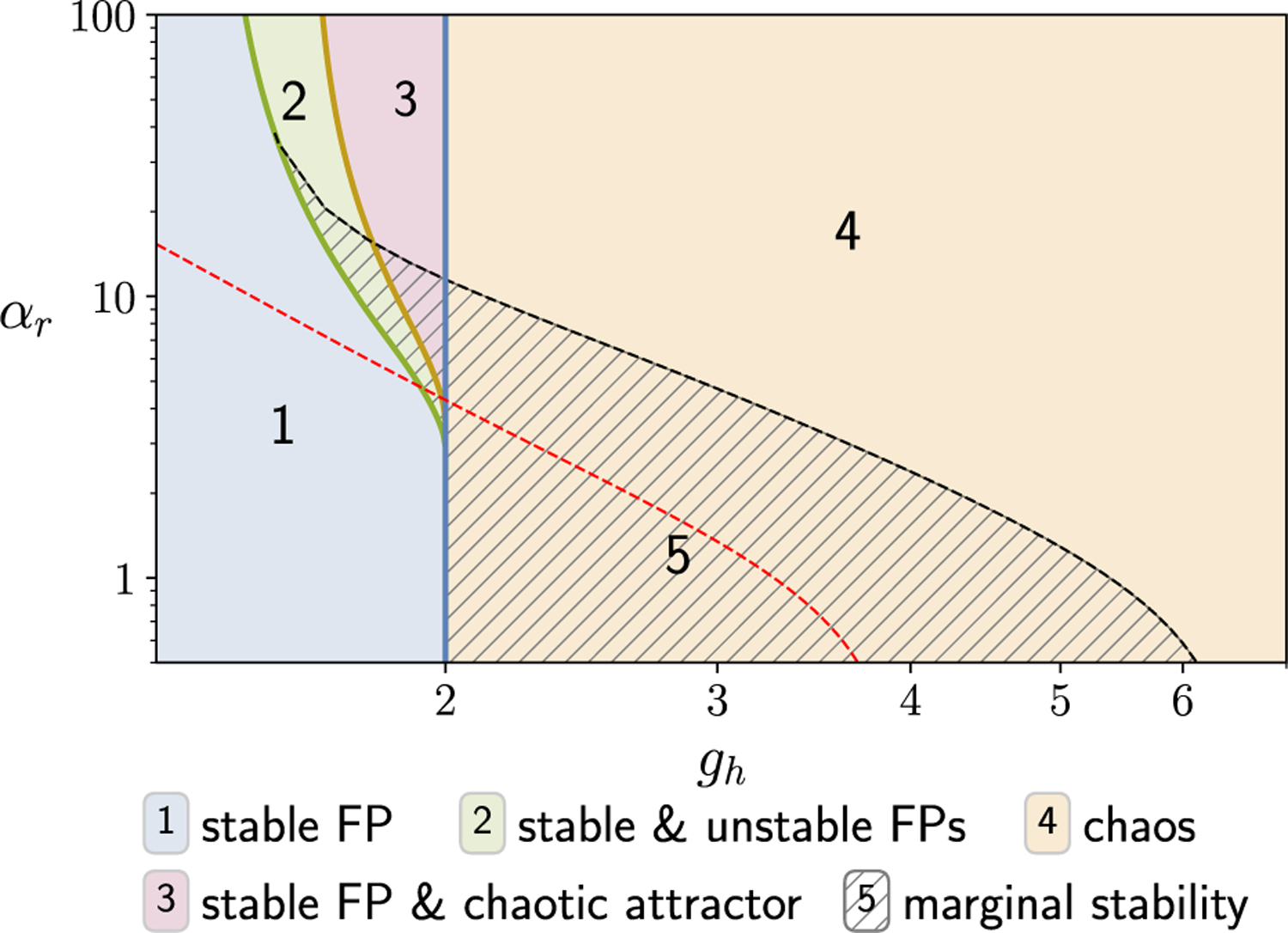
Phase diagram for the gated RNN. (a) (no biases) In regions 1 and 2, the zero FP is the global attractor of dynamics; however, in region 2, there is a proliferation of unstable FPs without any asymptotic dynamical signatures. In region 3, the (stable) zero FP coexists with chaotic dynamics. Note that the plotted curve separating regions 2 and 3 is computed for α_z = 0 and remains valid for sufficiently small values of α_z. In region 4, the zero FP is unstable, and dynamics are chaotic. For all parameter values in region 5, a previously unstable or chaotic state can be made marginally stable when α_z = ∞. For any given parameter values in region 5, there are infinitely many marginally stable points in the phase space to which the dynamics converge. The red dashed line indicates the critical transition between a stable fixed point (below the line) and chaos (above the line) in the presence of static random input (to the h variable) with standard deviation σ_h = 0.5. Note that, while chaos is suppressed for small α_r along the g_h axis, for larger α_r there are regions of stable FPs that become chaotic with finite input. This leads to the phenomenon of input-induced chaos.