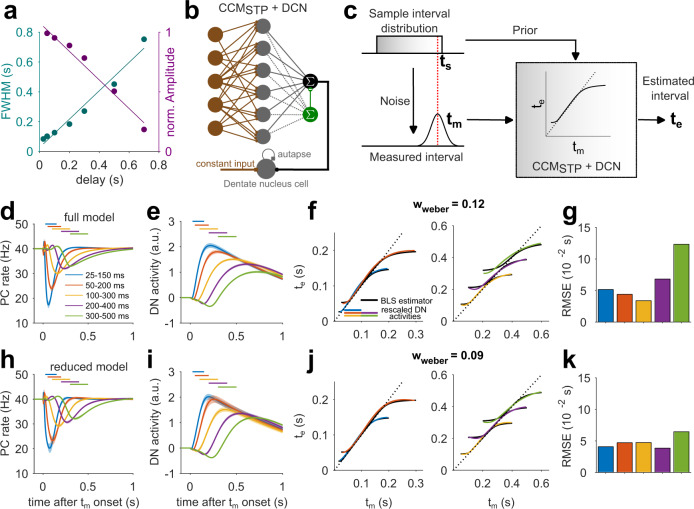
Fig. 6. STP-generated temporal basis enables the computation of Bayesian time-interval estimates.

a Full width at half maximum (cyan) and normalized amplitudes (magenta) of learned PC pauses versus delay interval from the experimentally constrained CCM_STP (see Fig. 2). Solid lines are linear fits. b Scheme of CCM_STP with added dentate nucleus cell. c Scheme of Bayesian integration. The sample interval t_s (red dashed line, here drawn from a uniform distribution, upper left) is subject to a noisy measurement yielding a measured interval t_m (lower left). CCM_STP implements Bayesian integration yielding an estimated interval t_e (right). d PC responses after 12,000 learning trials, averaged over n = 20 simulations with different realizations of MF patterns and MF-GC connectivity. Shaded area indicates standard deviation. Different colors represent learning of different uniform sample interval distributions. e Same as (d), but for DN cell activity. f Rescaled DN cell activity for different learned interval distributions (colored) and fitted theoretical Bayesian least squares (BLS) estimator (solid black line), with w_weber = 0.12 resulting from fit. g Squared deviation of rescaled DN activity from the BLS estimator for all tested intervals. h–k Same as (d–g), but for the reduced model. The reduced model firing rate parameters were μ_D = 200 Hz, μ_S = 20 Hz, σ_D=10Hz and σ_S = 15 Hz and resulted in DN activity consistent with a Bayesian least squares model with w_weber = 0.09.