Explicitly accounting for needle sugar pool size crucial for predicting intra‐seasonal dynamics of needle carbohydrates δ¹⁸O and δ¹³C

Summary

• We explore needle sugar isotopic compositions (δ¹⁸O and δ¹³C) in boreal Scots pine (Pinus sylvestris) over two growing seasons.

• A leaf‐level dynamic model driven by environmental conditions and based on current understanding of isotope fractionation processes was built to predict δ¹⁸O and δ¹³C of two hierarchical needle carbohydrate pools, accounting for the needle sugar pool size and the presence of an invariant pinitol pool.

• Model results agreed well with observed needle water δ¹⁸O, δ¹⁸O and δ¹³C of needle water‐soluble carbohydrates (sugars + pinitol), and needle sugar δ¹³C (R ² = 0.95, 0.84, 0.60, 0.73, respectively). Relative humidity (RH) and intercellular to ambient CO₂ concentration ratio (C _i/C _a) were the dominant drivers of δ¹⁸O and δ¹³C variability, respectively. However, the variability of needle sugar δ¹⁸O and δ¹³C was reduced on diel and intra‐seasonal timescales, compared to predictions based on instantaneous RH and C _i/C _a, due to the large needle sugar pool, which caused the signal formation period to vary seasonally from 2 d to more than 5 d. Furthermore, accounting for a temperature‐sensitive biochemical ¹⁸O‐fractionation factor and mesophyll resistance in ¹³C‐discrimination were critical.

• Interpreting leaf‐level isotopic signals requires understanding on time integration caused by mixing in the needle sugar pool.

Short abstract

See also the Commentary on this article by Ubierna et al., 236: 2003–2008.

Introduction

Stable carbon and oxygen isotope compositions in tree rings (δ¹³C and δ¹⁸O, respectively) provide records of past environmental and tree physiological signals (McCarroll & Loader, 2004; Battipaglia et al., 2013). Tree ring δ¹³C and δ¹⁸O records are foreseen as powerful tools in advancing our understanding on the response of forests to changing climate and increasing atmospheric CO₂ concentration (Gessler et al., 2014). The formation of tree ring δ¹³C and δ¹⁸O signals in boreal coniferous species is of special interest, because these sensitive ecosystems play a critical role in the carbon cycle of our planet (Snyder et al., 2004) and are now undergoing climatic warming at a significantly faster rate compared to the global average (IPCC, 2021). To this end, we need to understand how isotopic signals are formed in the leaves, where most of the interaction with local environmental conditions occurs. Even though, this is a vastly studied field, intra‐seasonal studies in boreal forest are scarce.

Newly assimilated photosynthates are products of atmospheric CO₂ and leaf water, thus reflecting δ¹³C of atmospheric CO₂ strongly modified by leaf biochemistry (Farquhar et al., 1982) and δ¹⁸O of source water that is further ¹⁸O‐enriched in leaves during evaporation (Farquhar & Lloyd, 1993). ¹⁸O‐enrichment due to evaporation is linked to the variation of relative humidity (RH) as defined by the model of Craig & Gordon (1965), developed for open water bodies and adapted later to leaves (Dongmann et al., 1974). The Craig–Gordon model is, however, prone to overestimate ¹⁸O‐enrichment (Cernusak et al., 2016), which has led to the introduction of the Péclet effect (Farquhar & Lloyd, 1993; Barbour et al., 2000) and the two‐pool concept (Leaney et al., 1985; Roden et al., 2015). The δ¹⁸O of leaf photosynthates is expected to reflect the δ¹⁸O of leaf water with an offset of 27‰ (Barbour et al., 2000; Cernusak et al., 2003). Although the offset 27‰ is commonly assumed constant, Sternberg & Ellsworth (2011) reported it to be inversely related to temperature, with a particularly strong incline below 20°C. Recently, Hirl et al. (2021) acknowledged the need to account for this temperature dependence, when modeling the seasonal variation of cellulose δ¹⁸O in a grassland ecosystem, underlining the power of modeling in testing our current theoretical understanding. In cooler boreal conditions, such temperature dependence is potentially of even higher importance.

Regarding δ¹³C, the pathway to primary photosynthates in C₃ plants can be divided into fractionation by diffusion from air to chloroplast through stomata and mesophyll, and biochemical fractionation, that is, carboxylation, mitochondrial respiration and photorespiration (Farquhar et al., 1982; Cernusak et al., 2013). Recent studies have emphasized the importance of dynamic mesophyll conductance on δ¹³C of assimilates (Stangl et al., 2019; Schiestl‐Aalto et al., 2021). Mechanistic modeling studies have further shown that tree ring δ¹³C signals are highly sensitive to isotopic fractionation during both photosynthesis and respiration (Ogée et al., 2009; Eglin et al., 2010) and that the sugars used for leaf respiration may have a δ¹³C value that differs from current assimilates (Wingate et al., 2007). These findings together with the fact that the fractionation factors of these processes are still poorly constrained in vivo (Barbour & Song, 2014), complicate modeling δ¹³C signals in plants.

Interpreting and predicting isotopic signals in leaves may be further complicated in field conditions with strong variability in environmental conditions over sub‐daily to seasonal timescales. For example, leaf water δ¹⁸O sampled on sub‐daily timescales in varying ambient conditions has been shown to deviate significantly from values predicted by a steady‐state model (Farquhar & Cernusak, 2005; Gessler et al., 2013). Similar nonsteady‐state effects are expected, when predicting the isotopic composition of leaf sugars as the sugar pool does not represent only the current assimilates (Barnard et al., 2007; Gessler et al., 2013). There are dynamic models describing intra‐seasonal variation in δ¹³C and δ¹⁸O in tree ring cellulose (e.g. Ogée et al., 2009; Eglin et al., 2010), but similar descriptions for leaf sugar pools are scarce. These earlier studies face the difficulty of differentiating between fractionation processes in the leaves and during the pathway to tree rings, which stresses the need for leaf‐level mechanistic models.

Measurements of the isotopic composition of leaf sugars is challenging in many respects. Primarily, studies often analyze only mixtures of compounds (e.g. total leaf organic matter, water‐soluble organic matter, or purified water‐soluble extracts), which tends to reduce the temporal variability of the isotopic signal of interest, as compounds within the mixture can have different live‐spans in the leaf and differ in their isotope value due to fractionations during secondary metabolism (Barnard et al., 2007; Offermann et al., 2011; Gessler et al., 2013; Rinne et al., 2015; Lehmann et al., 2020). Purified water extracts (hereafter water‐soluble carbohydrates, WSC) are expected to consist mainly of sugars (Richter et al., 2009; Rinne et al., 2015) and have therefore potentially more variable isotopic signal than total organic matter. However, if sugar alcohols (e.g. pinitol/myo‐inositol, hereafter referred to as pinitol; see Rinne et al., 2012) are present in high concentrations, they have been shown to reduce the variability of the δ¹³C signal of WSC (Richter et al., 2009; Rinne et al., 2015). Permanent high fraction of pinitol throughout the growing season is typical for conifer needles in high‐latitude and high‐elevation conditions (Lipavská et al., 2000; Streit et al., 2013; Rinne et al., 2015). To address this issue, compound‐specific isotope analysis (CSIA) of δ¹³C provides means to retrieve the isotopic signal of e.g. sucrose, the main transport sugar, from the bulk sample (Rinne et al., 2012). For δ¹⁸O, the analytical process is more laborious and only a few studies have reported CSIA results for a limited number of samples (Lehmann et al., 2016, 2017). Intra‐seasonal CSIA of δ¹⁸O are therefore still out of reach for modeling purposes. However, making use of the CSIA results of δ¹³C, compound concentrations, and concurrently analyzed δ¹³C and δ¹⁸O of WSC, mechanistic models can attempt to answer how variable δ¹⁸O is between various compounds.

This study explores the formation of needle sugar isotopic signals in boreal Scots pine over two growing seasons in southern Finland. We concurrently present observations and environmentally driven dynamic modeling of the intra‐seasonal variation of δ¹⁸O and δ¹³C of needle WSC. Our isotopic data consists of δ¹⁸O in water pools (e.g. twig and needle), δ¹⁸O and δ¹³C analyzed from WSC as bulk, and δ¹³C results from CSIA. Combining mechanistic modeling and data, we aim to address the following research questions:

• Which fractionation and mixing processes are important for capturing intra‐seasonal variation of needle sugar δ¹⁸O and δ¹³C?

• What is the role of the sugar pool size in predicting needle sugar δ¹⁸O and δ¹³C?

• What implications do needle sugar pool size and the composition of bulk samples have on interpreting environmental/physiological signals from needle δ¹⁸O and δ¹³C?

Model description

The built model describes the dynamics of δ¹⁸O and δ¹³C in two hierarchical needle carbohydrate pools in response to half‐hourly environmental conditions (air temperature, photosynthetic active radiation (PAR), vapor pressure, atmospheric CO₂ concentration, and soil moisture) and isotopic input data (δ¹⁸O of water vapor and source water, and δ¹³C of atmospheric CO₂). The two carbohydrate pools described in the model are needle: (1) sugars; and (2) WSC, which in addition to sugars contain pinitol. The model builds on a photosynthesis model solving leaf net CO₂ exchange, including carboxylation, photorespiration, and mitochondrial respiration (see Supporting Information Methods S1; Table S1). Doing so it accounts for stomatal control and mesophyll resistance, but neglects leaf energy balance assuming the leaf is at air temperature (a fair assumption, given the small size of Scots pine needles that are well‐coupled to the atmosphere; Launiainen et al., 2016; Kim et al., 2018). Theory‐based isotopic fractionation of oxygen and carbon in needles and their accumulation in the needle sugar and WSC pools are then solved as described in the following section. Model equations are expressed in terms of isotopic ratios (R), which can be converted to ‘delta’ notations:

$$\delta =\left(\frac{R}{R_{\mathrm{std}}}-1\right)$$ (Eqn 1)

where R _std is the isotope ratio of an international standard; Vienna Standard Mean Ocean Water (VSMOW) for ¹⁸O/¹⁶O and Vienna Peedee belemnite (VPDB) for ¹³C/¹²C.

Formation of needle sugar δ¹⁸O

In steady‐state conditions, the isotopic ratio of oxygen at evaporative sites is given by Flanagan et al. (1991)

$$R_{\mathrm{e},\mathrm{ss}}={\alpha }^{+}\left({\alpha }_{\mathrm{k}}\frac{w_{\mathrm{i}}-w_{\mathrm{a}}}{w_{\mathrm{i}}}{R}_{\mathrm{s}}+\frac{w_{\mathrm{a}}}{w_{\mathrm{i}}}{R}_{\mathrm{v}}\right)$$ (Eqn 2)

where R _s and R _v are the isotopic ratios of oxygen in source water and atmospheric water vapor, respectively; α ⁺ (= 1 + ε ⁺) is the temperature‐dependent equilibrium fractionation during vaporization (Majoube, 1971); w _a and w _i (in mol mol⁻¹) are the mole fractions of water vapor in the atmosphere and inside the leaf, respectively; and α _k is the kinetic isotope fractionation during water vapor diffusion through stomata and leaf boundary layer:

$${\alpha }_{\mathrm{k}}=1+\frac{g_{\mathrm{b}}{\epsilon }_{\mathrm{ks}}+g_{\mathrm{s}}{\epsilon }_{\mathrm{kb}}}{g_{\mathrm{b}}+g_{\mathrm{s}}}$$ (Eqn 3)

where g _s and g _b (in mol m⁻² s⁻¹) are stomatal and boundary layer conductances for CO₂ (assuming both scale for water vapor by 1.6); and ε _ks and ε _kb are the fractionation factors associated with the diffusion through stomata and the boundary layer, respectively (Table 1).

Table 1.

Parameters for isotopic modeling.

Parameter a	Description	Value	Source
$a_{\mathrm{b}}$ (−)	Fractionation during diffusion of CO2 through the boundary layer	2.9‰	Farquhar (1983)
$a_{\mathrm{s}}$ (−)	Fractionation during diffusion of CO2 through stomata	4.4‰	O'Leary (1981)
$a_{\mathrm{m}}$ (−)	Fractionation during transfer of CO2 through mesophyll	1.8‰	O'Leary (1984)
b (−)	Fractionation during caboxylation	29‰	Roeske & O'Leary (1984)
f (−)	Fractionation during photorespiration	8‰	Ghashghaie et al. (2003)
e (−)	Fractionation during mitochondrial respiration	–6‰	Ghashghaie et al. (2003)
δ13Cpin (−)	Pinitol δ13C in needle	−30.5‰	Measurements, see Fig. S2(d)
${\epsilon }^{+}$ (−)	Equilibrium fractionation during vaporization	–	Majoube (1971)
${\epsilon }_{\mathrm{kb}}$ (−)	Fractionation during diffusion of water vapor through boundary layer	19‰	Merlivat (1978)
${\epsilon }_{\mathrm{ks}}$ (−)	Fractionation during diffusion of water vapor through stomata	28‰	Merlivat (1978)
f 1 (−) b	Ratio of enriched to total needle water	0.93	Calibrated
L (m) c	Leaf mesophyll effective mixing length	0.03	Calibrated
W (mol m−2)	Leaf mesophyll water volume	5.6	Measurements, see Fig. S6
${\epsilon }_{\mathrm{wc}}$ (−)	Biochemical fractionation factor	27‰ ${\epsilon }_{\mathrm{wc}}\left(T\right)$	Sternberg et al. (1986) fig. 1 in Sternberg & Ellsworth (2011)
δ18Opin (−)	Pinitol δ18O in needle	25‰	Calibrated
S sug (μmol of C m−2)	Concentration of needle sugar	1.96 × 105	Measurements, see Fig. S5
S pin (μmol of C m−2)	Concentration of needle bulk sugars	0.7 S sug	Measurements, see Fig. S5(b)

^a Parameter units are given in parenthesis, where ‘–’ stand for unitless and all area‐based units refer to all‐sided leaf area.

^b Two‐pool approach.

^c Péclet approach.

Average mesophyll water (R _lw,ss) is less ¹⁸O‐enriched compared to the sites of evaporation, which at steady state is commonly formulated as a reduction factor (f ₁) above source water:

$$R_{\mathrm{lw},\mathrm{ss}}=f_1\left(R_{\mathrm{e},\mathrm{ss}}-R_{\mathrm{s}}\right)+R_{\mathrm{s}}$$ (Eqn 4)

There are two alternative concepts for defining f ₁: (1) the two‐pool model, where f ₁ is a constant (Leaney et al., 1985); and (2) the Péclet model, which relates f ₁ to transpiration (Farquhar & Lloyd, 1993). In the latter $f_1=\left(1-e^{-\wp }\right)/\wp$, where $\wp =\mathrm{EL}/\left(\mathrm{CD}\right)$; L (in meters) is the effective mixing length, E (in mol m⁻² s⁻¹) the transpiration rate, C (55.5 × 10³ mol m⁻³) the molar density of liquid water, and D (2.66 × 10⁻⁹ m² s⁻¹) the diffusivity of H₂ ¹⁸O in liquid water.

At sub‐daily timescales and at times of low transpiration, the steady‐state assumption may be violated because of the slow turn over rate of leaf water (Farquhar & Cernusak, 2005; Gessler et al., 2013). The formulation for the isotopic ratio of oxygen in leaf water under nonsteady state (R _lw) is given by (Farquhar & Cernusak, 2005)

$$\frac{{\mathit{dWR}}_{\mathrm{lw}}}{\mathit{dt}}=\frac{{\mathit{Ew}}_{\mathrm{i}}{f}_1}{{\alpha }^{+}{\alpha }_{\mathrm{k}}\left(w_{\mathrm{i}}-w_{\mathrm{a}}\right)}\left(R_{\mathrm{lw},\mathrm{ss}}-R_{\mathrm{lw}}\right)$$ (Eqn 5)

where W (in mol m⁻²) is the leaf water content.

New assimilates are generally assumed to be in oxygen isotopic equilibrium with bulk leaf water (Barbour et al., 2000): $R_{\text{assimilates}}={\alpha }_{\mathrm{wc}}{R}_{\mathrm{lw}}$, where α _wc (= 1 + ε _wc) is the biochemical fractionation associated with oxygen isotope exchange between carbonyl oxygen and water (Sternberg et al., 1986; Sternberg & Ellsworth, 2011). The signal of new assimilates is then carried to the needle sugar pool following Eqn 6, assuming that the needle sugar pool is well‐mixed and forms the substrate for mitochondrial respiration (Wingate et al., 2007; Ogée et al., 2009).

$$\frac{d\left(S_{\mathrm{sug}}{R}_{\mathrm{sug}}\right)}{\mathit{dt}}=\left(A_{\mathrm{n}}+r_{\mathrm{d}}\right)R_{\text{assimilates}}-r_{\mathrm{d}}{R}_{\mathrm{sug}}-{\mathit{qR}}_{\mathrm{sug}}$$ (Eqn 6)

where R _sug is the isotopic ratio in the needle sugar pool, S _sug (in μmol of C m⁻²) the concentration of needle sugar, A _n net CO₂ exchange, r _d mitochondrial respiration, and q the discharge of sugars from the needle into the phloem (all in μmol m⁻² s⁻¹). Finally, the isotopic ratio of needle WSC is computed as

$$R_{\mathrm{wsc}}=\frac{S_{\mathrm{sug}}{R}_{\mathrm{sug}}+S_{\mathrm{pin}}{R}_{\mathrm{pin}}}{S_{\mathrm{sug}}+S_{\mathrm{pin}}}$$ (Eqn 7)

where R _pin and S _pin (in μmol of C m⁻²) are the isotopic ratio and concentration of pinitol in the needle, respectively.

Formation of needle sugar δ¹³C

The model for ¹³C‐discrimination of net CO₂ exchange (${}^{13}\mathrm{\Delta }$, Eqn 8) was adopted from Wingate et al. (2007) (see also Methods S2). They modify the classical equation by Farquhar et al. (1982) to account for the fact that the δ¹³C composition of the substrate used for mitochondrial respiration may differ from that of current assimilates. Here we assume that substrate is the needle sugar pool. Unlike the formulation in Farquhar et al. (1982) that requires photosynthesis to model the δ¹³C of the respiratory substrates, this formulation is also valid in absence of photosynthesis (Wingate et al., 2007); during nighttime (k = 0), it simply reduces to the ¹³C‐discrimination of dark respiration.

$${}^{13}\mathrm{\Delta }=\frac{{\mathit{kC}}_{\mathrm{a}}}{{\mathit{kC}}_{\mathrm{a}}-r_{\mathrm{d}}}\left(a_{\mathrm{b}}\frac{C_{\mathrm{a}}-C_{\mathrm{s}}}{C_{\mathrm{a}}}+a_{\mathrm{s}}\frac{C_{\mathrm{s}}-C_{\mathrm{i}}}{C_{\mathrm{a}}}+a_{\mathrm{m}}\frac{C_{\mathrm{i}}-C_{\mathrm{c}}}{C_{\mathrm{a}}}+b\frac{C_{\mathrm{c}}}{C_{\mathrm{a}}}-f\frac{{\mathrm{\Gamma }}_{*}}{C_{\mathrm{a}}}\right)-\frac{r_{\mathrm{d}}}{{\mathit{kC}}_{\mathrm{a}}-r_{\mathrm{d}}}\left(\frac{R_{\mathrm{a}}}{R_{\mathrm{sug}}}\left(1+e\right)-1\right)$$ (Eqn 8)

where C _a, C _s, C _i and C _c (in μmol mol⁻¹) are CO₂ mole fractions in the atmosphere, at the leaf surface, in the intercellular spaces and in the chloroplasts; R _a and R _sug are isotopic ratios of CO₂ in ambient air and in the sugar pool; a _b, a _s, a _m, b, f and e are fractionation factors associated with diffusion through the boundary layer, diffusion through stomata, transfer through mesophyll, carboxylation, photorespiration, and mitochondrial respiration, respectively (Table 1); Γ _* (in μmol mol⁻¹) is the CO₂ compensation point in the absence of mitochondrial respiration (Bernacchi et al., 2001) and; k (= (A _n + r _d)/(C _c – Γ _*)) is the carboxylation efficiency. Eqn 8 ignores ternary effects as they are also ignored in modeling shoot gas exchange (Methods S1). Such approach is common for mechanistic modeling studies simulating both gas exchange and ¹³C‐discrimination (Ogée et al., 2009; Schiestl‐Aalto et al., 2021). According to Farquhar & Cernusak (2012) ignoring or accounting for ternary effects consistently in both gas exchange and discrimination calculations lead to almost equivalent results, whereas their inconsistent use in either gas exchange or discrimination calculations produce misleading results. Eqn 8 further assumes there is effectively only one carbon pool, where carbon compounds left behind by respiratory processes mix with the pool of respiratory substrate and carbon in the Calvin–Benson–Bassham (CBB) cycle. Busch et al. (2020) recently suggested an alternative model where respiration is isotopically disconnected and metabolites are not fed back into the CBB cycle, but this possibility was not included in our analysis.

The isotopic ratio of net CO₂ exchange is R _a/(1 + ¹³Δ), thus the isotopic signal of carbon in the needle sugar pool is solved from:

$$\frac{d\left(S_{\mathrm{sug}}{R}_{\mathrm{sug}}\right)}{\mathit{dt}}=A_{\mathrm{n}}\frac{R_{\mathrm{a}}}{\left(1+{}^{13}\mathrm{\Delta }\right)}-{\mathit{qR}}_{\mathrm{sug}}$$ (Eqn 9)

The δ¹³C of the needle WSC pool is computed as for oxygen (Eqn 7). The right‐hand side of Eqn 9 is equivalent to $\left(A_{\mathrm{n}}+r_{\mathrm{d}}\right)R_{\text{assimilates}}-r_{\mathrm{d}}\left(1-e\right)R_{\mathrm{sug}}-{\mathit{qR}}_{\mathrm{sug}}$.

Materials and Methods

Study site and measurements

Site description

The study site is the Station for Measuring Forest Ecosystem‐Atmosphere Relations (SMEAR II) in Hyytiälä, southern Finland (61°51′N, 24°17′E; Hari & Kulmala, 2005). The site is a managed boreal forest on a shallow mineral soil, with an overstorey dominated by 60‐yr‐old Scots pines (Pinus sylvestris L.). The long‐term (1981–2010) mean annual temperature and precipitation is 3.5°C and 711 mm, respectively (Pirinen et al., 2012). Snow typically covers the ground from December to April.

Shoot gas exchange

Shoot gas exchange measurements were performed with an automated chamber system (Aalto et al., 2014) consisting of a chamber, sample tubing and a gas analyzer. The box shaped shoot chamber (2.1 dm³) made of acrylic plastic and inner surfaces coated with fluorinated ethylene propylene (FEP) film was installed in the uppermost canopy. The chamber enclosed a 1‐yr‐old (in 2018) shoot in horizontal position. The inserted shoot was debudded before the chamber installation to prevent new growth. The chamber was open most of the time exposing the shoots to ambient conditions and closed intermittently for 1 min 50–90 times d^–1. Sample air was drawn from the chamber along polytetrafluoroethylene tubes (internal diameter 4 mm, length 73 m) to a gas analyzer (LI‐840; Li‐Cor, Lincoln, NE, USA) and compensated by ambient air leaking freely into the chamber. Fluxes of CO₂ and water were determined by fitting a nonlinear equation to concentration records during the first 5–35 s of chamber closure (Kolari et al., 2012). Water fluxes were rejected when RH was > 85% due to considerable adsorption of water on the chamber walls. Fluxes were calculated for all‐sided needle area (Kolari et al., 2007) and re‐sampled to half‐hourly time series. Based on all‐sided needle area measurements the specific leaf area was 0.010 m² g⁻¹. Resulting data coverage for fluxes of CO₂ and water were 98% and 63%, respectively, for mid‐April to mid‐October in 2018–2019.

Sampling and isotopic analysis of water

Samples of 1‐yr‐old needle (1N) water, twig water, soil water and atmospheric water vapor were collected every 3–5 wk during May–October in 2018 and 2019, except for 1N water sampled more frequently in 2019 (14 times + diurnal course on 23 May). Furthermore, 1N and twig samples were collected from five mature Scots pine trees between midday and 15:00 h (utc + 2) from a sun‐exposed position in canopy top. For each tree, 1N samples and the linked twigs with barks peeled off were collected into separate 12 ml exetainer vials (Labco, Lampeter, UK). Soil samples were cored using a foot‐step soil probe from three spots close to the sampled trees. Subsamples were taken from 2, 10 and 18 cm depths, and placed into individual exetainers. Water vapor was collected at 18 m height by pumping air for 2 to 3 h through a hose into a glass U‐tube, which was immersed in a mixture of dry ice and ethanol. Additionally, monthly precipitation samples were collected from May 2018–December 2019 using an evaporation‐free rainwater collector (Gröning et al., 2012). All collected samples were placed in a cool box with ice blocks immediately in the field and stored at −20°C.

Water vapor and precipitation (May–November 2018) samples were melted and transferred into 2 ml vials and analyzed for δ¹⁸O at the Stable Isotope Laboratory of Luke (SILL, Helsinki, Finland) by HT‐EA‐IRMS, that is, high temperature (HT) elemental analyzer (Sercon Ltd, Crewe, UK) connected to isotope ratio mass spectrometry (20–22 IRMS; Sercon). The results were calibrated against two in‐house reference waters. Water from plant and soil samples was cryogenically extracted by vacuum distillation (West et al., 2006). The δ¹⁸O of plant and soil extracted water of samples from 2018 were determined at the Stable Isotope Research Laboratory of WSL (Birmensdorf, Switzerland) (Lehmann et al., 2020), while corresponding samples from 2019 and precipitation from December 2018 to December 2019 were analyzed at the Stable Isotope Laboratory of University of Basel, Switzerland. For all samples, measurement precision derived from repeated measurements and a quality control water sample was 0.3‰ or better.

Sampling and isotopic analysis of water‐soluble needle carbohydrates

Current‐year needles (0N) and/or 1N were collected c. 20 times during May to October in 2018 and 2019 (+ diurnal course on 25 July 2019), from five trees during same time and canopy position as for water sampling. Samples were placed in a cool box with ice blocks immediately after collection and microwaved at 600 W for 1 min within 2 h to stop enzymatic and metabolic activities (Wanek et al., 2001). Samples were subsequently dried at 60°C for 24 h and homogenized into a fine powder by a ceramic‐ball mill using FastPrep‐24TM. Extraction and purification of WSC were performed according to Wanek et al. (2001) and Rinne et al. (2012). Shortly, the supernatant from the water extraction at 85°C was separated and purified using three types of sample treatment cartridges, which removed amino acids, organic acids and phenolic compounds. The purified samples were freeze‐dried, dissolved in Milli‐Q water, filtered through a 0.45 μm syringe filter (Acrodisc; Pall Corp., Port Washington, NY, USA) and stored at −20°C.

Bulk isotope analysis of WSC was performed at SILL. Before analysis, aliquots of solubilized extracted WSC were pipetted into individual tin and/or silver capsules (IVA Analysentechnik, Meerbusch, Germany), lyophilized and wrapped. The δ¹³C values were determined using EA‐IRMS (samples of 2018) or concurrently with δ¹⁸O analysis by HT‐EA‐IRMS using the dual isotope method (samples of 2019; Woodley et al., 2012). The EA‐IRMS results for δ¹³C were calibrated against IAEA‐C7 (−32.15‰), IAEA‐CH3 (−24.72‰) and an in‐house sucrose (−12.22‰; Sigma‐Aldrich) reference materials. The dual isotope measurements (δ¹⁸O and δ¹³C) were calibrated against IAEA‐601 (23.14‰ and −28.81‰), in‐house sucrose (36.62‰ and −12.22‰) and lactose (21.05‰ and −24.66‰) standards (Sigma‐Aldrich). Additionally, a subset of the samples were analyzed for δ¹³C using both the EA and the HT‐EA method to calibrate the HT‐EA results for δ¹³C (Woodley et al., 2012). Analytical precision of the measurements was 0.2‰ or better for δ¹³C and δ¹⁸O, determined from repeated measurements of a quality control standard.

Compound‐specific isotope analysis of δ¹³C was performed for the WSC samples of 2018 only, as analysis of samples of 2019 were delayed due to instrumental problems. CSIA was done at WSL using a Delta V Advantage IRMS (Thermo Fisher Scientific, Waltham, MA, USA) coupled to a high‐performance liquid chromatography (HPLC) system with a Finnigan LC Isolink interface (Thermo Fisher Scientific) (Rinne et al., 2012). The δ¹³C values were determined for the four detected sugars or sugar‐like compounds: sucrose, glucose, fructose and pinitol. External compound‐matched standard solutions with comparable concentration (20–180 ng C μl⁻¹) and δ¹³C values, as determined by EA‐IRMS, were analyzed between every 10 samples to correct the CSIA results (Rinne et al., 2012). The measurement precision (standard deviation, SD) of sucrose, glucose, fructose and pinitol standards were 0.44‰, 0.57‰, 0.88‰, and 0.38‰, respectively.

The concentration of each four individual compounds from HPLC‐IRMS were calculated using its peak area, and the linear regression between the carbon content and peak area of the compound‐matched standard (Rinne et al., 2012). The concentration of bulk WSC was calculated from the ratio of the sample weight in the tin/silver capsule to the sample weight used for the hot water extraction.

Based on CSIA, needle sugars comprised mainly of sucrose, while the total contribution of glucose and fructose was on average 25%. The concentration‐weighted average δ¹³C of the sugars was highly correlated with δ¹³C of sucrose (r > 0.95; Fig. S1), and hence δ¹³C of sucrose is used to indicate the δ¹³C of the total needle sugars hereafter.

The δ¹⁸O and δ¹³C of bulk WSC, and δ¹³C of sucrose and pinitol were each combined over the two needle generations (0N and 1N) to form time series covering the whole growing season (Fig. S2). The δ¹⁸O of bulk WSC and δ¹³C of sucrose were similar for 0N and 1N and the combined dataset was obtained as their average (Fig. S2a,c). Bulk WSC in 2018 and pinitol showed a difference in level of δ¹³C between 0N and 1N, which was first corrected for before averaging over the two data series (Fig. S2b,d).

Model runs, parameterization and evaluation

The model was ran for the two growing seasons, 2018–2019, using half‐hourly meteorological data measured above the canopy. Additionally, soil moisture from c. 5 cm depth in mineral soil was used as proxy for water availability limiting photosynthesis during dry conditions (Eqn S10 in Methods S1; Launiainen et al., 2022). Isotopic input data was not measured at the site at the resolution needed for the modeling. The δ¹⁸O of water vapor (six‐hourly) was obtained from the isotope‐enabled, nudged atmospheric general circulation model IsoGSM (Yoshimura et al., 2011, 2008), which corresponded reasonably well to the limited number of observations (Fig. S3). The δ¹⁸O of source water was modeled at daily resolution based on monthly precipitation δ¹⁸O, the amount of precipitation, soil moisture and eddy covariance‐based evapotranspiration, resulting in a good fit with the observed twig water δ¹⁸O (see Methods S3; Fig. S4). Lastly, δ¹³C of atmospheric CO₂ was available at weekly resolution from Pallas‐Sammaltunturi GAW‐station (White et al., 2015).

Initially, the model results related to leaf gas exchange (A _n, E and C _i/C _a) were evaluated against shoot chamber measurements. Thereafter, the results of the isotopic model were compared against measured δ¹⁸O of leaf water, δ¹⁸O and δ¹³C of needle WSC, and δ¹³C of needle sugars. The model fit was evaluated using mean absolute error (MAE) and R ².

The parameters applied in the isotopic modeling are listed in Table 1. The measured WSC concentrations indicated little variability during the growing seasons (Fig. S5a). The concentrations fluctuated c. 95 mg g⁻¹, which corresponds to 3.33 × 10⁵ μmol of C m⁻², when using the measured specific leaf area (0.010 m² g⁻¹) and the molecular mass of carbon in sucrose 28.5 g (mol C)⁻¹ (similar to 27.7 and 30 g (mol C)⁻¹ for pinitol and glucose/fructose, respectively). The ratio of pinitol to total sugar concentration was also rather invariant during the measurement period, especially after the beginning of July (Fig. S5b). The ratio was c. 0.7, meaning that sugars accounted for 59% of WSC and pinitol for 41%. Thus, S _sug was defined as a constant (Table 1) and hence the discharge from the sugar pool in Eqns 6 and 9 was set equal to net CO₂ exchange (q = A _n). Lastly, pinitol δ¹³C was set to −30.5‰ based on CSIA results (Fig. S2d), whereas pinitol δ¹⁸O was calibrated in the absence of CSIA results for oxygen.

For both oxygen and carbon isotopic models, we applied a selection of model variants to understand the role of different processes in capturing intra‐seasonal variation of needle sugar δ¹³C and δ¹⁸O. For oxygen, the model variants for needle water δ¹⁸O included the Craig–Gordon model (Eqn 2), the two‐pool model (Eqn 4 with constant f ₁) and the Péclet model (Eqn 4 with transpiration‐dependent f ₁). Each of these models were run both in steady and nonsteady state. Furthermore, to predict needle WSC δ¹⁸O, we tested the model with a constant and a temperature‐dependent ε _wc (Table 1); and by defining the size of the sugar pool corresponding to the measurements (Table 1) or as a 20‐fold smaller value. The latter resulted in δ¹⁸O of leaf water with an offset of ε _wc (or δ¹³C of net CO₂ exchange) to be approximately equal to the isotopic values of the needle sugar pool (i.e. all sugars in needle represent current assimilates).

For carbon, we tested how much neglecting mesophyll resistance affects the model results by assuming C _c = C _i. The importance of photorespiration and mitochondrial respiration were tested by setting f and r _d to zero, respectively. With f = r _d = 0, Eqn 8 reduces to its most simple formulation. In addition to b = 29‰, this most simple formulation was ran with b = 27‰ and C _c = C _i, where the lower b implicitly accounts for all isotopic effects that happen during photosynthetic discrimination including the contribution of mesophyll resistance (Farquhar et al., 1982; Ubierna & Farquhar, 2014). With r _d = 0, Eqn 8 reduces to the commonly applied formulation that only accounts for diffusion, carboxylation and photorespitation (e.g. Seibt et al., 2008), whereas setting e = 0 would still consider the release of respired CO₂ into intercellular spaces (Wingate et al., 2007). Finally, as for oxygen, the effect of the size of the sugar pool was investigated.

Evaluating formation period and environmental/physiological signals

For model results and observations, we examined the relationships between isotopic signals and environmental/physiological variables, that is, needle sugar δ¹⁸O against RH and δ¹³C against C _i/C _a. Pearson's correlation coefficient (r) was used to quantify the strength of the linear relationship.

To account for the integration over time in the needle sugar pool, we calculated a weighted mean of past RH and C _i/C _a based on the same assumptions as implemented in the model (i.e. well‐mixed sugar pool of constant size). The implicit solution of Eqn 6 (or Eqn 9 when neglecting e) defines the sugar pool signal at time t as:

$$R_{\mathrm{sug}}^t={\alpha }^t{R}_{\text{assimilates}}^t+\left(1-{\alpha }^t\right)R_{\mathrm{sug}}^{t-1}$$ (Eqn 10)

where $\alpha =\left(A_{\mathrm{n}}+r_{\mathrm{d}}\right)/\left(S_{\mathrm{sug}}/\mathrm{\Delta }t+A_{\mathrm{n}}+r_{\mathrm{d}}\right)$ and Δt (in seconds) is the time interval between t − 1 and t. Applying Eqn 10 recursively the sugar pool signal can be written as a weighed mean of past time instances $R_{\text{assimilates}}$.

$$R_{\mathrm{sug}}^t=\sum _{n=0}^{\tau }\left(w_{\mathrm{n}}{R}_{\text{assimilates}}^{t-n}\right)/\sum _{n=0}^{\tau }{w}_{\mathrm{n}}$$ (Eqn 11)

where τ is the number of time steps to consider (here cut off at ${\sum }_{n=0}^{\tau }{w}_{\mathrm{n}}\approx 0.95$) and w _n is the weight of the signal at time t – n expressed as:

$$w_{\mathrm{n}}={\alpha }^{t-n}\times \prod _{i=0}^{n-1}\left(1-{\alpha }^{t-i}\right)$$ (Eqn 12)

Eqn 11 was used to calculate a weighted RH and C _i/C _a by replacing R by RH and C _i/C _a, respectively. Furthermore, the length of the signal formation period (τΔt) over the two growing seasons was examined. For step‐by‐step derivation of Eqns (Eqn 10), (Eqn 11), (Eqn 12) see Methods S4.

Results

Environmental conditions and shoot gas exchange

The 2018 growing season was hotter and drier than 2019, as indicated by higher temperature and vapor pressure deficit (VPD), and lower top soil moisture (Fig. 1a,b). May–September precipitation was higher in 2018 (345 mm) than in 2019 (293 mm), but it was more evenly distributed in 2019 (not shown). During both years, temperature and VPD reached maximum values in July and PAR followed a bell‐shape reaching highest values in June (Fig. 1a,b). Shoot transpiration and net CO₂ uptake had distinct seasonal cycles with highest daily fluxes reached in late June to mid‐July (Fig. 1c,e). Low soil moisture in August–September 2018 (Fig. 1b) limited photosynthesis, as shown by model runs with and without considering the water limitation (black vs gray lines in Fig. 1c,e). The value of C _i/C _a was also affected by the water limitation (Fig. 1g). Overall, the model reproduced shoot gas exchange well (Fig. 1d,f,h). At half‐hourly timescale, R ² for transpiration and net CO₂ uptake were 0.86 and 0.90, respectively.

Fig. 1.

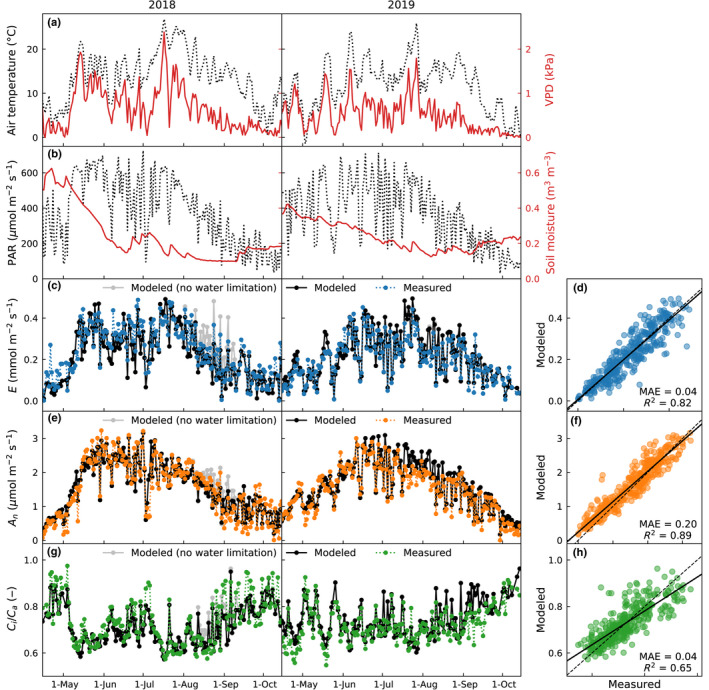
Environmental conditions and Scots pine shoot gas exchange during mid‐April to mid‐October 2018 and 2019. Daily mean (a) air temperature and vapor pressure deficit (VPD), and (b) photosynthetically active radiation (PAR) and soil moisture at 5 cm depth. Modeled and measured (c) transpiration, E, (e) net CO₂ uptake, A _n, and (g) intercellular to ambient CO₂ concentration ratio, C _i/C _a. E and A _n are presented as daily means of times with observations and C _i/C _a as daily medians for time when sun is above horizon. Model results neglecting the water limitation from soil moisture are shown in gray in (c, e, g). The fit between modeled and measured values is examined in (d, f, h), where the dashed line is 1 : 1 and the solid line the linear least squares regression. R ² and MAE denote the coefficient of determination and mean absolute error, respectively.

The δ¹⁸O of needle water, sugars and water‐soluble carbohydrates

Measured needle water δ¹⁸O varied between −10‰ and 15‰ during the study period (Fig. 2a), whereas needle WSC δ¹⁸O was much less variable, 23–34‰ (Fig. 2b). Modeled needle water δ¹⁸O for the entire studied period (including periods between measurements) showed larger variability than measurements (Fig. 2a) because only a few sampling days occurred during low relative humidity (early July 2018 and late growing season of 2019). However comparing only data from sampling days, the model results (including Péclet effect with nonsteady state and a temperature‐dependent ε _wc) well reproduced the seasonal variability in needle water and WSC δ¹⁸O (Fig. 2a,b), explaining 95% (Fig. 3f) and 84% (Fig. 3a,d) of their variability, respectively. In order to capture the measured needle WSC δ¹⁸O, the δ¹⁸O of pinitol was adjusted to 25‰, suggesting ¹⁸O‐depletion of pinitol in comparison to sugars. Hence, the variability of needle WSC δ¹⁸O was reduced compared to the variability modeled for needle sugar δ¹⁸O (Fig. 2b).

Fig. 2.

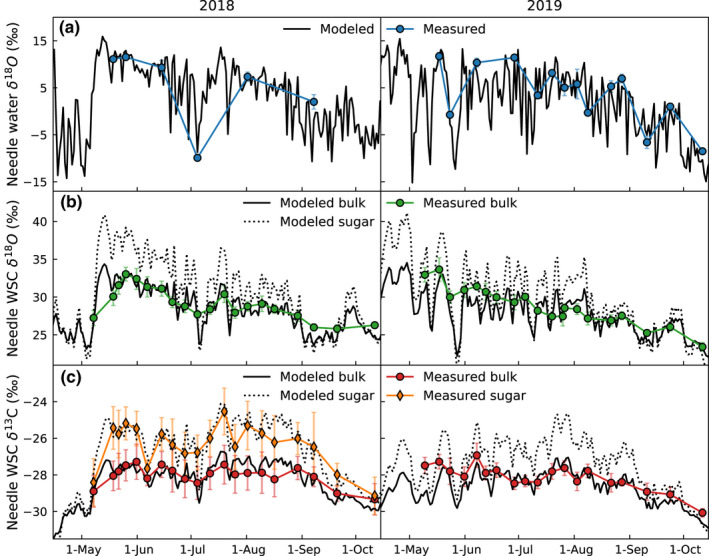
Modeled and measured (a) needle water δ¹⁸O, (b) δ¹⁸O of needle sugar and in bulk water‐soluble carbohydrates (WSC), and (c) δ¹³C of needle sugar and in bulk WSC of Scots pine. Modeled values are given as mean of 12:00–15:00 h, which corresponds to sampling interval. Error bars indicate the SDs of the five sampled trees.

Fig. 3.

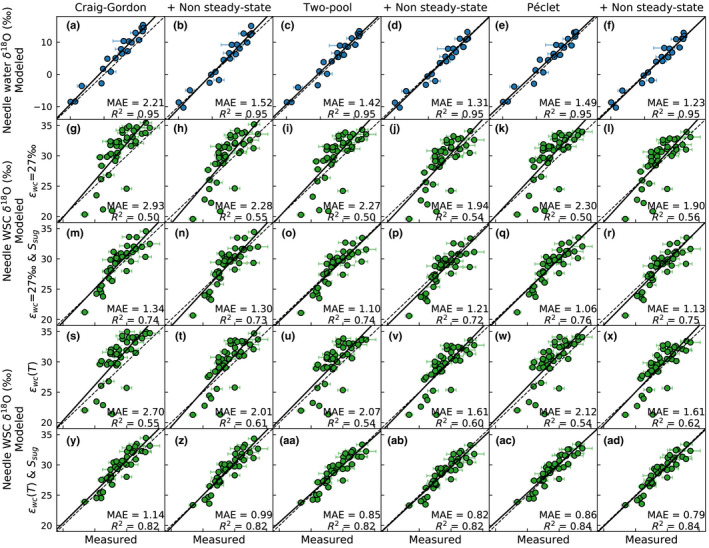
The fit between modeled and measured Scots pine (a–f) needle water δ¹⁸O, and (g–ad) δ¹⁸O of needle water‐soluble carbohydrates (WSC) with different needle water modeling approaches (see column titles) and model processes affecting δ¹⁸O of needle WSC. In (g–r) the biochemical fractionation factor, ε _wc, is constant (27‰) and in (s–ad) ε _wc is temperature dependent following Sternberg & Ellsworth (2011). In (m–r) and (y–ad) the needle sugar pool size is set according to measurements, while in (g–l) and (s–x) its size is negligible. The dashed line is 1 : 1 and the solid line the linear least squares regression. R ² and MAE denote the coefficient of determination and mean absolute error, respectively. Modeled values are given as mean of 12:00–15:00 h, which corresponds to sampling interval. Error bars indicate the SDs of the five sampled trees.

The different needle water model variants did not affect the amount of variation captured by the model (R ² = 0.95, Fig. 3a–f). The level of needle water δ¹⁸O was best captured with either the two‐pool or the Péclet model under nonsteady state assumption (MAE = 1.23–1.31‰, Fig. 3d,f), whereas the Craig–Gordon model produced the highest overestimation (Fig. 3a,b). The nonsteady state assumption was also supported by the sampled diel needle water δ¹⁸O variation during May 23, 2019 (Fig. S7).

Accounting for the sugar pool size had a significant impact on the fit between modeled and measured δ¹⁸O of needle WSC. For example, with constant ε _wc, R ² improved from c. 0.5 (Fig. 3g–l) to 0.72–0.76 (Fig. 3m–r), when the sugar pool size was set according to measurements instead of a negligible size. The model fit improved further when the temperature‐dependent ε _wc was implemented, resulting in R ² ranging from 0.82 to 0.84 (Fig. 3y–ad).

The δ¹³C of needle sugars and water‐soluble carbohydrates

The temporal variability of observed δ¹³C of needle bulk WSC was much smaller, with values ranging from −29‰ to −27‰ than that of needle sugar, with values ranging from −29‰ to −24.5‰ (Fig. 2c). This was expected due to the presence of pinitol with a near constant δ¹³C. The model explained 73% and 60% of the variability in δ¹³C of needle sugar and bulk WSC, respectively (Fig. 4n).

Fig. 4.

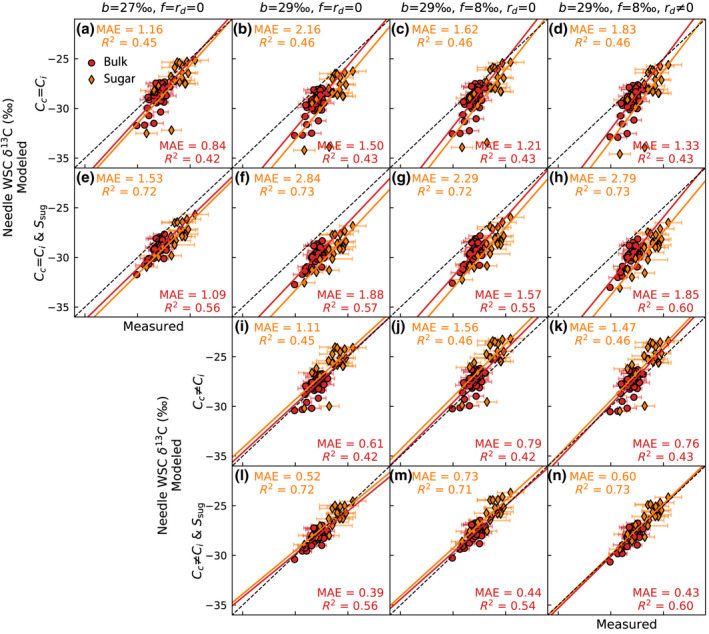
The fit between modeled and measured Scots pine δ¹³C of needle sugar and in bulk water‐soluble carbohydrates (WSC) with different model variants. The first column shows the commonly applied simple formulation, where the lower b implicitly accounts for all photosynthetic discrimination processes. The second column accounts only for fractionation by diffusion and carboxylation, the third adds photorespiration, and the last the effect of mitochondrial respiration. In (a–h) the models are based on C _c = C _i and in (i–n) the effect of mesophyll resistance is explicitly accounted for. Lastly, in (e–h) and (l–n) the needle sugar pool size is set according to measurements, while in (a–d) and (i–k) its size is negligible. The dashed line is 1 : 1 and the solid line the linear least squares regression. R ² and MAE denote the coefficient of determination and mean absolute error, respectively. The upper corner values correspond to sugar and those in lower corner to bulk WSC. Modeled values are given as mean of 12:00–15:00 h, which corresponds to sampling interval. Error bars indicate the SDs of the five sampled trees.

Evaluating the model variants for δ¹³C of needle sugar and WSC, we observe, as for δ¹⁸O, that accounting for the sugar pool size is important. The value of R ² for needle sugar improved from 0.45–0.46 to 0.71–0.73, when the sugar pool size was accounted for (Fig. 4a–d, i–k vs e–h, l–n, respectively). Applying the model without explicitly accounting for mesophyll resistance captured 72–73% of the variability in observed needle sugar δ¹³C (Fig. 4e–h). However, in this case, the predicted values were generally too low (Fig. 4d–f) and only the simple model showed a slope close to unity (Fig. 4e). Explicitly accounting for mesophyll resistance (C _c ≠ C _i) increased the predicted δ¹³C, which decreased MAE but did not improve R ² (Fig. 4e–h vs l–n). Similarly, including photorespiration (f = 8‰) had no effect on the variability captured by the model (Fig. 4f,l vs g,m). Then again, including the effect of mitochondrial respiration (r _d ≠ 0) slightly improved R ², especially for δ¹³C of WSC (Fig. 4g,m vs h,n), which covered two growing seasons, unlike δ¹³C of needle sugar (Fig. 2c). Overall, the best result (highest R ² and lowest MAE) was obtained in Fig. 4(n) (b = 29‰, f = 8‰, r _d ≠ 0 and C _c ≠ C _i), which corresponds to the time‐series shown in Fig. 2(c).

Needle sugar pool size and formation period of isotopic signals

As expected, modeling results with a negligible needle sugar pool size showed much larger variability than results obtained applying the observed sugar pool size (Fig. 5a,b). However, during times when day‐to‐day meteorological conditions were fairly stable, e.g. second half of May and early June 2018 (Fig. 1a,b), the role of the sugar pool size was less evident. Then again, the isotopic signal formed during occasional days of low VPD and PAR were not imprinting the sugar pool, because photosynthesis was typically low during these days and hence the role of current assimilates on shaping the isotopic composition of the sugar pool remained small (Fig. 5). The dynamics of the results obtained applying the observed sugar pool size were overall lagged and smoother compared to results with a negligible sugar pool size, especially in early and late growing season when the formation period of the sugar pool isotopic signal was longer (Fig. 5c). During mid‐growing season the sugar pool was formed of photosynthates assimilated over the past 48–52 h, while in early and late growing season the length of the formation period increased to over 5 d (Fig. 5c).

Fig. 5.

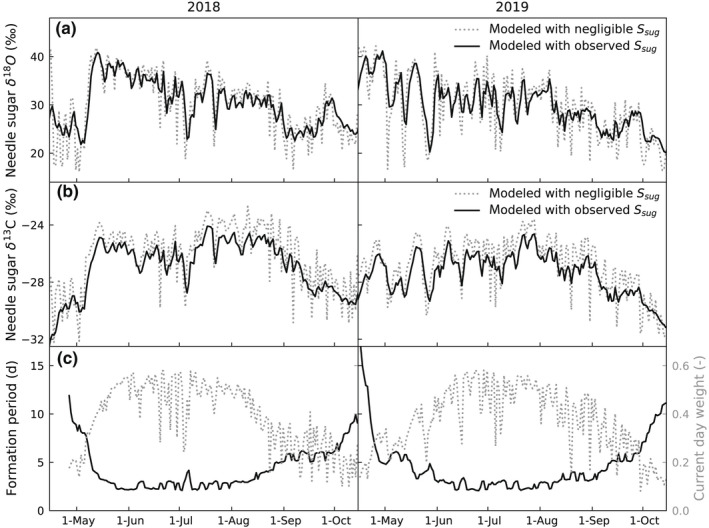
Modeled needle sugar (a) δ¹⁸O and (b) δ¹³C of Scots pine at 13:30 h with negligible sugar pool size and the observed sugar pool size. Panel (c) presents the formation period of the needle sugar pool isotopic signals and the weight of the current day assimilates in forming the isotopic signal of the needle sugar pool. The formation period and the current day weight were calculated assuming the sugar pool is well‐mixed and its size set equal to observed (see text).

The differences between the two modeling scenarios shown in Fig. 5(a,b) are not only caused by the combined effect of the sugar pool and day‐to‐day variation in meteorological conditions, but also the role the sugar pool has on the diurnal course of isotopic signals. Fig. 6 shows the modeled diurnal course of needle water δ¹⁸O + ε _wc and of δ¹³C of net CO₂ exchange, which during daytime correspond to the sugar pool δ¹⁸O and δ¹³C, respectively, if the sugar pool size were negligible. In comparison to these, the modeled diurnal course of the sugar pool isotopic signals (applying the observed sugar pool size) are lagged and have a much lower amplitude. For δ¹³C this causes the 1–2‰ offset between the two scenarios in Fig. 5(b) as in the early afternoon δ¹³C of net CO₂ exchange is higher compared to that of the sugar pool (Fig. 6b). For δ¹⁸O, the δ¹⁸O of needle water + ε _wc crosses the value of the sugar pool δ¹⁸O around midday (Fig. 6a) and hence Fig. 5(a) does not show a similar offset between the two modeling results as for δ¹³C. The δ¹⁸O and the δ¹³C of needle WSC measured from diurnal samples during July 25, 2019 support the low diurnal amplitude obtained by the model (Fig. 6a,b).

Fig. 6.

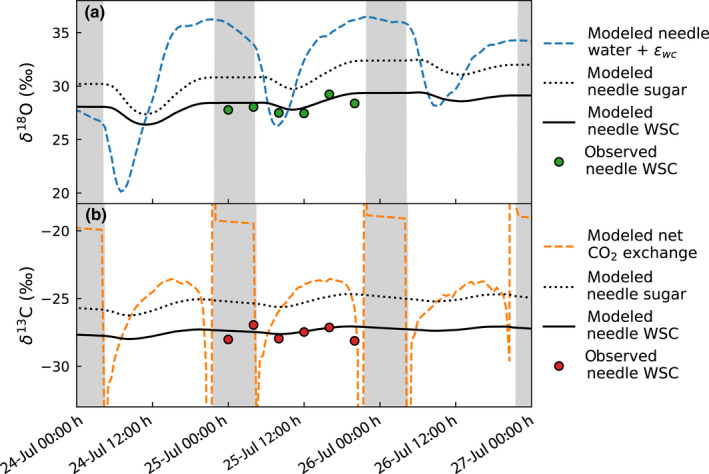
Modeled diurnal course of (a) δ¹⁸O and (b) δ¹³C signals in Scots pine needles during 24–26 July 2019 and measured needle isotopic signals of water‐soluble carbohydrates (WSC) sampled during 25 July 2019. In addition to modeled needle sugar and bulk WSC signals, (a) shows the isotopic signal of needle water + ε _wc (biochemical fractionation factor) and (b) the isotopic signal of net CO₂ exchange. Gray‐shaded areas indicate night‐time. Extreme high and low values during the transition between day and night are caused by noise in model results when kC _a – r _d tends to zero (see Eqn 8).

Environmental and physiological signals

The δ¹⁸O and relative humidity

Both measured and predicted δ¹⁸O of needle water correlated strongly with the sampling day RH (Fig. 7a). The correlation between δ¹⁸O of needle WSC and RH was, however, weaker, and deviated from the expected relationship with RH observed for needle water δ¹⁸O offset by 27‰ (Fig. 7b). The modeled δ¹⁸O of needle sugar deviated less from this relationship but showed a lot of scatter (Fig. 7d). Both for modeled and measured δ¹⁸O, the correlations improved considerably, when we used the weighting scheme outlined earlier for RH to account for the sugar pool being an integration over time (Fig. 7b,d vs c,e). Also, accounting for the integration, the relationship between needle sugar δ¹⁸O and RH follows the expected line (Fig. 7e).

Fig. 7.

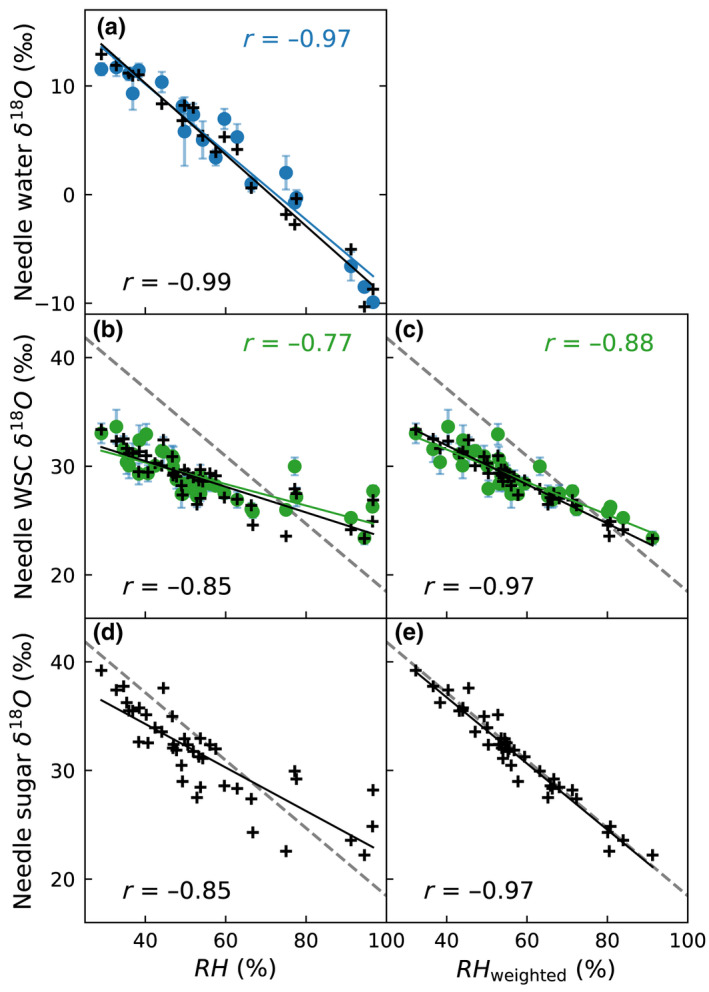
Relationship between relative humidity (RH) and (a) needle water δ¹⁸O, (b–c) δ¹⁸O of needle water‐soluble carbohydrates (WSC), and (d–e) needle sugar δ¹⁸O of Scots pine. In (a, b, d) RH corresponds to the sampling day (mean of midday ± 3 h) and in (c, e) RH is obtained by the weighting scheme outlined in the text. Colored dots and correlations (r) given in upper corner correspond to measurements, and plus‐signs and r given in lower corner to modeled values. The gray dashed line (b–e) indicates the relationship in (a) +27‰. Error bars indicate the SDs of the five sampled trees.

The δ¹³C and C _i/C _a

Relationships between δ¹³C and C _i/C _a showed a similar response as δ¹⁸O to RH; the variability of needle bulk WSC δ¹³C was reduced compared to that of needle sugar (Fig. 8a,b vs c,d), and the correlation strength increased once time integration was considered (Fig. 8a,c vs b,d).

Fig. 8.

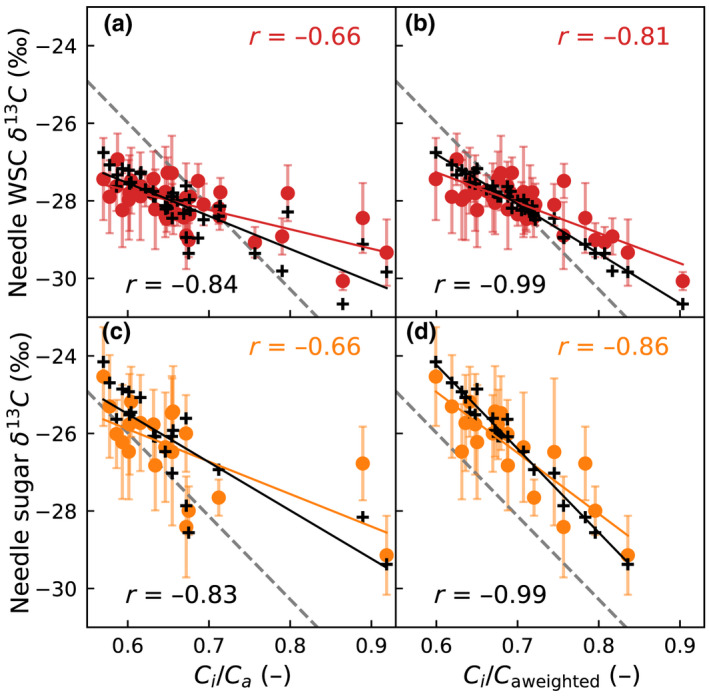
Relationship between modeled intercellular to ambient CO₂ concentration ratio (C _i/C _a) and (a–b) δ¹³C of needle bulk WSC, and (c–d) needle sugar δ¹³C of Scots pine. In (a, c) C _i/C _a corresponds to the sampling day (mean of midday + 3 h) and in (b, d) C _i/C _a is obtained by the weighting scheme outlined in the text. Colored dots and correlations (r) given in upper corner correspond to measurements, and plus‐signs and r given in lower corner to modeled values. The gray dashed line corresponds to the simple model: ¹³Δ = a _s + (b – a _s)C _i/C _a, with b = 27‰, a _s = 4.4‰ and δ¹³C of atmospheric CO₂ set to its mean value −8.5‰. Error bars indicate the SDs of the five sampled trees.

The relationships in Fig. 8 are compared against the expected δ¹³C vs C _i/C _a relationship (dashed gray line) defined following the simple model: ¹³Δ = a _s + (b – a _s)C _i/C _a, with b = 27‰ and δ¹³C of atmospheric CO₂ set to its mean value −8.5‰. The slope of this relationship is well represented by the observed and modeled needle sugar δ¹³C in Fig. 8(d), whereas Fig. 8(a–c) deviate from it because of neglecting the effect of time integration and/or because of the presence of pinitol. The miss‐match in level of c. 1.5‰ in Fig. 8(d) is in line with Fig. 4(e).

Discussion

Evidence for temperature‐dependent biochemical fractionation factor

Modeling of needle water δ¹⁸O indicated that its variation was strongly dictated by RH, as both RH (Fig. 7a) and the applied models (Fig. 3a–f) explained c. 95% of the variation of needle water δ¹⁸O (Roden & Ehleringer, 1999). Hereby at our study site, the variation in δ¹⁸O of water vapor and source water had only minor role, which supports the reconstruction of RH from tree ring δ¹⁸O records (Anderson et al., 1998; Wright & Leavitt, 2006). For water vapor δ¹⁸O we used IsoGSM data (Yoshimura et al., 2008), a good proxy at our study site (Fig. S3), thus not assuming vapor‐source water isotopic equilibrium (R _v = R _s/α ⁺, Ogée et al., 2009). Leaf water δ¹⁸O is known to be rather insensitive to water vapor δ¹⁸O, because the ¹⁸O kinetic fractionation dominates over vapor‐source water isotopic disequilibrium (Cernusak et al., 2016). Then again, the minor role of source water δ¹⁸O was caused by its limited variability compared to the variability of evaporative ¹⁸O‐enrichment (Belmecheri et al., 2018). However, this does not necessarily hold, e.g. at sites where plant water sources vary between isotopically distinct precipitation and melting permafrost (Saurer et al., 2016).

In line with earlier studies, we found that the Craig–Gordon model overestimated needle water δ¹⁸O (Cernusak et al., 2016). We could not distinguish whether the two‐pool or the Péclet model provided a more suitable correction as, when calibrated, both models resulted in more or less equally good results (Fig. 3c–f). This has been typical also in earlier studies, but in some cases calibration has led to unrealistic parameter values (Song et al., 2013; Roden et al., 2015). The parameters obtained by calibration here, f ₁ = 0.93 and L = 30 mm, are reasonable in comparison to measured leaf anatomical characteristics (Roden et al., 2015; Timofeeva et al., 2020). However, there exist uncertainties related to the calibrated parameter values due to, e.g. the assumption of leaf temperature being equal to air temperature (Ogée et al., 2009; Cernusak et al., 2016) and the source of diffusional fractionation factors (Merlivat, 1978; Cappa et al., 2003).

Based on the diurnal course of needle water δ¹⁸O (Fig. S7), we recognized the need for the nonsteady‐state model (Barnard et al., 2007; Gessler et al., 2013). However, its impact on δ¹⁸O of needle sugar was less critical (Fig. 3ac vs ad), because during times of highest assimilation δ¹⁸O of needle water was close to the steady‐state solution. This suggests steady‐state leaf water models could be sufficient in predicting plant cellulose δ¹⁸O (Ogée et al., 2009; Hirl et al., 2021), simplifying model structure and parametrization needs.

One of our key findings was that implementing the temperature‐dependent biological fractionation factor (ε _wc), following results from laboratory experiments by Sternberg & Ellsworth (2011), improved predictions of needle WSC δ¹⁸O notably (Fig. 3m–r vs y–ad). So far only one study (Hirl et al., 2021) has shown such evidence in field conditions and our study is the first to show this for trees. For our study site, with May–September temperatures varying between −2.9 and 30.7°C, ε _wc ranged from 34.6 to 25.4‰. Although this has important implications to predicting plant δ¹⁸O signals, here the implemented temperature dependence did not clearly interfere with the dominant effect of RH in driving needle sugar δ¹⁸O variability (Fig. 7e). The influence of the temperature‐dependent ε _wc is however expected to be critical in climate and leaf temperature reconstruction studies spanning across various temperature zones. For example, as shown by Sternberg & Ellsworth (2011), the temperature‐dependent ε _wc may explain the unexpected strong correlation between mean annual temperature and cellulose ¹⁸O‐enrichment found across 39 tree species at 25 sites by Helliker & Richter (2008).

A challenge of this study was that δ¹⁸O was not measured for needle sugars, but only for bulk WSC. We assumed that WSC consisted of sugars reflecting needle water δ¹⁸O and pinitol with a constant δ¹⁸O. To capture the observed WSC δ¹⁸O, pinitol δ¹⁸O was adjusted to 25‰, which is reasonable compared to the 22‰ reported for pinitol in Siberian larch (Lehmann et al., 2017). However, Lehmann et al. (2017) also found differences between δ¹⁸O of sucrose (most ¹⁸O‐enriched), fructose and glucose, thus there remains some uncertainty in whether it is only the relatively high amounts of ¹⁸O‐depleted pinitol that causes the reduced variation in δ¹⁸O of needle WSC. While the modeling suggested ¹⁸O‐depleted pinitol as one plausible explanation, further compound specific δ¹⁸O analyses are needed to verify our finding.

Mesophyll resistance has important role in determining the level of needle sugar δ¹³C

The C _i/C _a was the dominant driver of δ¹³C variation in the modeled needle carbohydrate pools as expected (Farquhar et al., 1982). Increasing model complexity provided only limited improvement to the explained variation. Interestingly, we found that the simple model with the bulk fractionation factor b = 27‰ (Fig. 4e; Farquhar et al., 1982; Ubierna & Farquhar, 2014) captured the variability almost as well as the comprehensive model (Fig. 4n) and only showed a fairly constant offset of 1.5‰. This indicates that changes in C _i/C _a can be derived from changes in needle sugar δ¹³C using the simple model (¹³Δ = 4.4 + (27 – 4.4)C _i/C _a). However, explicitly accounting for mesophyll resistance (i.e. C _c ≠ C _i), was required to capture the absolute level of observed δ¹³C (Warren et al., 2003; Ubierna & Marshall, 2011; Gentsch et al., 2014). The chosen description for mesophyll conductance (Eqn S9 in Methods S1) also played a key role as it defines C _c ≈ 0.8C _i (Fig. S8a). By contrast, applying a constant mesophyll conductance (e.g. Wingate et al., 2007; Ogée et al., 2009) or a constant ratio between stomatal and mesophyll conductance (e.g. Vernay et al., 2020) result in C _c approaching C _i at high C _i (Fig. S8b,c), which would have led to poorer model agreement, as there was a miss‐match in δ¹³C values along the whole range of C _i/C _a (Fig. 8d). This underlines the need for better understanding on the variability of mesophyll conductance at intra‐seasonal scale.

Need to account for needle sugar pool size to predict its isotopic composition

For both δ¹⁸O and δ¹³C, results indicated clearly that the needle sugar pool size has a crucial role in reducing its day‐to‐day (Fig. 5a,b) and sub‐daily (Fig. 6) variation of isotopic composition compared to that of new assimilates. In line with the ¹³C‐pulse‐labeling study on Pinus pinaster by Desalme et al. (2017), we suggest that the signal of the sugar pool was composed of sugars assimilated over the past 48 h to more than 5 d depending mostly on the time of the growing season (Fig. 5c). While time lags and attenuated diurnal patterns between, e.g. leaf water and leaf organic matter δ¹⁸O are commonly recognized (Barnard et al., 2007; Gessler et al., 2013), their causes have not been quantitatively attributed to the sugar pool size, as done here using dynamic modeling. Examining our results at different timescales provides vital information for the interpretation of leaf‐level isotopic data. For example: (1) the difference between instant leaf water δ¹⁸O and leaf sugar δ¹⁸O seldom equals ε _wc (Figs 5a, 6a; Gessler et al., 2013; Lehmann et al., 2017); (2) online measured δ¹³C of net CO₂ exchange (e.g. Wingate et al., 2007; Schiestl‐Aalto et al., 2021) is expected to be higher than δ¹³C of needle sugar sampled in early afternoon (Fig. 6b); and (3) sudden day‐to‐day variations in meteorological conditions are not strongly reflected in isotopic signals of the needle sugar pool (Fig. 5a,b). Explicitly attributing such phenomena to the simple accumulation and mixing of new assimilates in the needle sugar pool is highly relevant to avoid miss‐interpreting fractionation processes in leaves.

The applied assumption that needle sugars form one well‐mixed pool of constant size may be debatable. It has been suggested that sucrose appears both in a fast transport pool and a slow transport pool (Brauner et al., 2014; Bögelein et al., 2019), which would reduce the variation in needle sugar δ¹³C further compared to our predictions. The concept of various transport pools might become critical when predicting isotopic compositions further downstream from leaves (e.g. phloem or tree ring cellulose), but here at leaf‐level its role could not be identified. Also, the concentration of needle sugars is expected to vary diurnally (Liesche et al., 2021) and seasonally with increased levels at the start and end of growing season (Schiestl‐Aalto et al., 2019). With high needle sugar concentrations, typical for trees growing under cold winters (Fig. S5; Kagawa et al., 2006; Rinne et al., 2015), we can however expect the diurnal variation in concentration to be small compared to the absolute concentration value. For the seasonal variation, our data showed no clear pattern (Fig. S5), plausibly indicating that during the active growing season, which is the crucial period for tree ring formation, the assumption of constant sugar pool size is sufficient.

Time integration and sample composition critical for retrieving environmental/physiological signals from needle δ¹⁸O and δ¹³C

The correlations between δ¹⁸O and RH, and δ¹³C and C _i/C _a further underlined the need to account for the needle sugar pool being an integration over time (Figs 7b–e, 8). The correlations were clearly weaker, when examined against sampling day RH and C _i/C _a compared to RH and C _i/C _a weighted according to past assimilation and mixing in the sugar pool. The correlation strength between δ¹³C and C _i/C _a did not clearly differ for needle WSC and needle sugars (Fig. 8), which supports our assumption on constant pinitol share and pinitol δ¹³C. The main difference between needle WSC and needle sugars was the slope of the relationships, which for WSC deviated from the expected relationships due to the presence of depleted pinitol (Figs 7c, 8b). This emphasizes the need to know the sample composition, in order to draw conclusions about the magnitude of underlying environmental/physiological changes causing the variation of the isotopic signals (Stokes et al., 2010; Tarin et al., 2020). If the constant share and isotopic signal of pinitol are known, one can estimate changes in RH or C _i/C _a from bulk WSC δ¹⁸O or δ¹³C, respectively, as the isotopic signal of needle sugar is a linear function of that of bulk WSC (Eqn 7).

Examining the environmental/physiological signals both for model results and observations provided means to explain the phenomena behind the present relationships or the lack of them (see also Hirl et al., 2021). Such evaluation is valuable and has potential to bridge the gap between empirical studies, focused on the climatic signals of tree ring isotopic records, and mechanistic modeling studies, in order to further advance the interpretation of isotopic signals in trees.

Competing interests

None declared.

Author contributions

KL, SL and KTR‐G designed the study. KTR‐G planned the sampling scheme and led the analysis of isotopic data. YT, PS‐A, ES and KTR‐G conducted the fieldwork, YT conducted laboratory preparation of samples, and ES, MS and AK performed the isotope analysis. PK processed the shoot chamber data. KL analyzed the data with assistance from YT and PK, and built the model and run it with guidance from JO, SL and PS‐A. All authors participated in interpreting the results and writing the manuscript in the lead of KL.

Supporting information

Fig. S1 Measured needle sucrose δ¹³C against measured needle sugar (sucrose + glucose + fructose) δ¹³C in current‐year needles and 1‐yr‐old needles.

Fig. S2 Measured isotopic composition of needle water‐soluble carbohydrates in current‐year needles and 1‐yr‐old needles, and a combined data series over the two needle generations.

Fig. S3 Measured δ¹⁸O of atmospheric water vapor against corresponding values predicted by IsoGSM.

Fig. S4 Modeled and measured source (twig) water δ¹⁸O and observed soil water δ¹⁸O.

Fig. S5 Measured concentrations of needle water‐soluble carbohydrates and measured ratio of needle pinitol to needle sugar (sucrose + glucose + fructose) concentrations in current‐year needles and 1‐yr‐old needles.

Fig. S6 Measured water content of 1‐yr‐old needles.

Fig. S7 Modeled and measured diurnal course of needle water δ¹⁸O.

Fig. S8 Modeled relationship between CO₂ mole fraction in chloroplast and intercellular spaces using different descriptions for mesophyll conductance.

Methods S1 Modeling shoot gas exchange.

Methods S2 Derivation of model for ¹³C‐discrimination of net CO₂ exchange (Eqn 8).

Methods S3 Modeling source water δ¹⁸O.

Methods S4 Derivation of Eqns (Eqn 10), (Eqn 11), (Eqn 12).

Table S1 Parameter values applied for shoot gas exchange modeling.

Please note: Wiley Blackwell are not responsible for the content or functionality of any Supporting Information supplied by the authors. Any queries (other than missing material) should be directed to the New Phytologist Central Office.

Data availability

The model code was written in Python and is available at https://github.com/LukeEcomod/LeafIsotopes with an example run corresponding to this study. Environmental and eddy‐covariance data for the study site (SMEAR II Hyytiälä forest) can be obtained from https://smear.avaa.csc.fi/. The isotopic and concentration data are available on request to the corresponding author.