Summary
Marginal structural models (MSMs), which adopt inverse probability treatment weighting in the estimating equations, are powerful tools to estimate the causal effects of time-varying exposures in the presence of time-dependent confounders. Motivated by the Conservation of Hearing Study (CHEARS) Audiology Assessment Arm (AAA) where repeated hearing measurements were clustered by study participants, time, and testing sites, we propose two methods to account for the multilevel correlation structure when fitting the MSMs. The first method directly models the covariance of the repeated outcomes when solving the weighted generalized estimating equations for MSMs, while the second two-stage analysis approach fits cluster-specific MSMs first and then combines the estimated parameters using mixed-effects meta-analysis. Finite sample simulation results suggest that our methods can obtain less biased and more efficient estimates of the parameters by accounting for the multilevel correlation. Moreover, we explore the effects of using fixed- or mixed-effects model to estimate the treatment probability on the parameter estimates of the MSMs in the presence of unmeasured cluster-level confounders. Lastly, we apply our methods to the CHEARS AAA data set, to estimate the causal effects of aspirin use on hearing loss.
Keywords: Audiometric data, Clustered data, Marginal structural models, Meta-analysis, Multilevel correlation, Weighted GEE
1. Introduction
Marginal structural models (MSMs) are a class of causal models that can estimate the causal effects of time-varying exposures when there exists time-dependent confounders (Robins, 2000; Robins and others, 2000). The MSMs adopt inverse probability of treatment weighting in the estimating equations to create a pseudo-population in which there is no confounding such that the causal parameters can be consistently estimated. Hernan and others (2002) extended the MSMs to the setting with repeated measurements to estimate the causal effect of zidovudine therapy on mean CD4 counts using patients’ data from 16 clinical visits, and the causal parameters were estimated using a weighted generalized estimating equations (GEE) approach, with the diagonal elements of the weight matrix reflecting the inverse of the treatment history probability until the corresponding visit. When fitting the weighted GEE, a working covariance matrix needs to be specified, and Hernan and others (2002) adopted a simple working independent covariance matrix, which would lead to efficiency loss. Compared with their data, where there was only one level of correlation induced by within-person repeated measures, we focus on data with multiple levels of correlation and account for the multilevel correlation structure when estimating the causal effects of the time-varying treatments to make full use of the available information. The first method that we propose is to model the correlation directly by adopting an appropriate working covariance matrix when fitting the weighted GEE on the whole data set, while the second method, which is named the “two-stage analysis approach,” fits separate MSMs for each cluster first, and in the second stage, combines the cluster-specific causal parameters using a mixed-effects meta-analysis. Moreover, in the presence of unmeasured cluster-level confounders, we propose to use fixed-effects or mixed-effects models to estimate the treatment probabilities such that the unmeasured cluster-level confounders can be accounted for.
This article is motivated by the Conservation of Hearing Study (CHEARS), which evaluated risk factors of hearing loss among participants in the Nurses’ Health Studies II (NHS II), an ongoing cohort study consisting of 116 430 female registered nurses in the United States, aged 25–42 years at enrollment in 1989 (Curhan and others, 2018). In NHS II, participants filled in questionnaires for lifestyle information every 2 years, and dietary variables were obtained through semiquantitative food frequency questionnaires every 4 years. The CHEARS Audiology Assessment Arm (AAA) is a subcohort of NHS II, that assessed the longitudinal changes in pure-tone air and bone conduction audiometric hearing thresholds (Curhan and others, 2020). In CHEARS AAA, baseline hearing testings were completed on 3749 participants, and the 3-year follow-up testings were completed on 3136 participants; these testings were performed at 34 different testing sites. A three-level correlation structure may exist in the hearing threshold data, where the first layer of correlation exists between the two ears for a given individual at a particular time, and the second layer of correlation lies in the measurements taken at different times of the AAA for a given individual, while the third layer of correlation is the hearing threshold measurements of different individuals from the same testing site.
The article is organized as follows. In Section 2, we introduce the notation, basics of MSMs, and the causal Directed Acyclic Graph (DAG) representing the AAA data set. In Section 3, we propose two methods to account for multilevel correlation when fitting the MSMs. In Section 4, we perform simulation studies to evaluate the finite sample performance of the two proposed methods. As an illustrative example, in Section 5, we estimate the causal effect of aspirin use on the change in hearing threshold based on the CHEARS AAA data. Section 6 concludes the article.
2. Notations and basics of MSMs
We adapt the notation from Hernan and others (2002) with an extension to multilevel data and describe our methods using a data set with a three-level correlation. Our methods will also apply to data with more than three-level correlation. Let  denote the time points that data were collected,
denote the time points that data were collected,  denote the treatment received by unit
denote the treatment received by unit 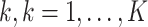 , of subject
, of subject  from cluster
from cluster  at time
at time  . Note that the unit is nested within the subject and the subject is further nested within a larger cluster
. Note that the unit is nested within the subject and the subject is further nested within a larger cluster  . Throughout the article, cluster is used only to indicate the largest clusters that contain all the possible layers of correlation. For instance, in the AAA, cluster is used to represent the testing site. Let
. Throughout the article, cluster is used only to indicate the largest clusters that contain all the possible layers of correlation. For instance, in the AAA, cluster is used to represent the testing site. Let  denote the corresponding continuous outcome and
denote the corresponding continuous outcome and  be a column vector containing all the covariates and confounders for the
be a column vector containing all the covariates and confounders for the  th unit of the
th unit of the  th subject within cluster
th subject within cluster  at time
at time  . Finally, we use the overbar to denote the covariate history. For example,
. Finally, we use the overbar to denote the covariate history. For example,  represents the observed treatment/exposure history until time
represents the observed treatment/exposure history until time  for the corresponding unit. We will not distinguish between treatment and exposure in this article.
for the corresponding unit. We will not distinguish between treatment and exposure in this article.
For each unit, define the treatment regime as  , where
, where 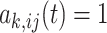 if the unit
if the unit  of subject
of subject  from cluster
from cluster  has the treatment at time
has the treatment at time  . The counterfactual outcome
. The counterfactual outcome  at time
at time 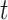 denotes the outcome had they had the treatment regime
denotes the outcome had they had the treatment regime  , which might be different from the true observed treatment. The causal effects of the treatment regime can be defined for a specific unit as:
, which might be different from the true observed treatment. The causal effects of the treatment regime can be defined for a specific unit as:  for
for  . In this article, we focus on the average treatment effect (ATE) of the regime in the population:
. In this article, we focus on the average treatment effect (ATE) of the regime in the population:
 |
In our motivating example,  , with
, with  representing the time at the last NHS II questionnaire return before the start of AAA,
representing the time at the last NHS II questionnaire return before the start of AAA,  representing the baseline of AAA,
representing the baseline of AAA,  being the time at the questionnaire return during the follow-up period of AAA, and
being the time at the questionnaire return during the follow-up period of AAA, and 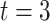 represents the end of 3 years of the follow-up period of AAA. We define the unit as people’s left (
represents the end of 3 years of the follow-up period of AAA. We define the unit as people’s left ( ) or right ear (
) or right ear ( ) with study participants being subjects indexed by
) with study participants being subjects indexed by  , and the testing sites where the study participants had their hearing tests conducted being clusters indexed by
, and the testing sites where the study participants had their hearing tests conducted being clusters indexed by  . Note that the hearing tests were only conducted at baseline and end of AAA (
. Note that the hearing tests were only conducted at baseline and end of AAA ( and
and  ), while exposures and other covariates were available at
), while exposures and other covariates were available at  through the questionnaires. In this hearing loss study, the treatment/exposure and other covariates were on the individual level, however our methods can be applied to data with ear-level covariates. Figure 1 presents a simplified DAG corresponding to the AAA, and a more detailed DAG was provided in the Supplementary material available at Biostatistics online, and due to the clustering induced by different testing sites, we include an additional cluster-level unmeasured confounder
through the questionnaires. In this hearing loss study, the treatment/exposure and other covariates were on the individual level, however our methods can be applied to data with ear-level covariates. Figure 1 presents a simplified DAG corresponding to the AAA, and a more detailed DAG was provided in the Supplementary material available at Biostatistics online, and due to the clustering induced by different testing sites, we include an additional cluster-level unmeasured confounder  , which is associated with both the exposures and outcomes.
, which is associated with both the exposures and outcomes.
Fig. 1.
DAG for AAA.  contain the confounders at different times, such as gender, race, etc.;
contain the confounders at different times, such as gender, race, etc.;  represent the treatment a study participant takes such as Aspirin;
represent the treatment a study participant takes such as Aspirin;  and
and  are the hearing measurements for the left and right ears obtained at the baseline and end of AAA and U represents the testing site-level confounders. Note that, in our study, the left and right ear received the same treatment at a particular time while for general cases, different units may receive different treatments.
are the hearing measurements for the left and right ears obtained at the baseline and end of AAA and U represents the testing site-level confounders. Note that, in our study, the left and right ear received the same treatment at a particular time while for general cases, different units may receive different treatments.
To model the counterfactual mean of the repeated measurements, the following MSM model can be assumed:
 |
(2.1) |
where 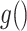 is a known function and
is a known function and  is a vector containing the parameters to be estimated, with the
is a vector containing the parameters to be estimated, with the  th element denoted as
th element denoted as  . For instance, Hernan and others (2002) adopted a cumulative sum of the treatment history:
. For instance, Hernan and others (2002) adopted a cumulative sum of the treatment history:
 |
(2.2) |
such that  reflects the cumulative effect of the treatment regime
reflects the cumulative effect of the treatment regime  on the counterfactual mean of the outcome up to time
on the counterfactual mean of the outcome up to time  in the whole population. Moreover, the MSM can be extended to allow for interactions between treatments and some pretreatment covariates
in the whole population. Moreover, the MSM can be extended to allow for interactions between treatments and some pretreatment covariates  if effect modification exists (Robins and others, 2000; Hernan and others, 2002).
if effect modification exists (Robins and others, 2000; Hernan and others, 2002).
To consistently estimate the causal effects of exposures from an observational study, the following assumptions need to be satisfied.
• Assumption 1
Stable unit treatment value assumption (SUTVA)
SUTVA assumes that a subject’s counterfactual outcome  is the observed outcome
is the observed outcome  for the treatment regime
for the treatment regime  that they actually took and is not affected by other subjects’ exposures/treatment (Imbens and Rubin, 2015).
that they actually took and is not affected by other subjects’ exposures/treatment (Imbens and Rubin, 2015).
• Assumption 2
No unmeasured confounding.
There is no unmeasured confounding when the following conditional independence holds:
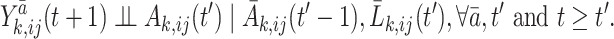 |
The unmeasured confounding assumption indicates that given the treatment and covariate history until time  and
and  , respectively, all future counterfactual outcomes are independent of the current treatment.
, respectively, all future counterfactual outcomes are independent of the current treatment.
• Assumption 3
Positivity.
If  , then
, then  , where
, where  is the density function. The positivity assumption ensures that all treatment regimes can be observed in the data.
is the density function. The positivity assumption ensures that all treatment regimes can be observed in the data.
When Assumptions 1–3 hold, the causal effects  of the treatment regime on the repeated measurements can be estimated by solving the following weighted GEE (Hernan and others, 2002)
of the treatment regime on the repeated measurements can be estimated by solving the following weighted GEE (Hernan and others, 2002)
 |
(2.3) |
where  contains the observed measurements for the
contains the observed measurements for the  th subject of the
th subject of the  th cluster across all units and times;
th cluster across all units and times;  is the corresponding working variance–covariance matrix of the repeated measurements, and Hernan and others (2002) used a working independent covariance matrix. Here,
is the corresponding working variance–covariance matrix of the repeated measurements, and Hernan and others (2002) used a working independent covariance matrix. Here,  is a column vector containing the corresponding expected value of the outcomes,
is a column vector containing the corresponding expected value of the outcomes,  , and
, and  is the diagonal weighting matrix, with the
is the diagonal weighting matrix, with the  th diagonal element, denoted as
th diagonal element, denoted as  or
or 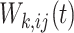 , being the weight assigned to the outcome of unit
, being the weight assigned to the outcome of unit  measured at time
measured at time  :
:
 |
(2.4) |
where  for all subjects (Hernan and others, 2002). Moreover, the parameters in (2.3) could be estimated using an iterative approach (Prentice and Zhao, 1991).
for all subjects (Hernan and others, 2002). Moreover, the parameters in (2.3) could be estimated using an iterative approach (Prentice and Zhao, 1991).
The denominator in (2.4) can vary significantly across subjects if  is strongly associated with
is strongly associated with  , leading to large variability (Robins and others, 2000). Therefore, the following stabilized weights were recommended (Robins and others, 2000; Hernan and others, 2002):
, leading to large variability (Robins and others, 2000). Therefore, the following stabilized weights were recommended (Robins and others, 2000; Hernan and others, 2002):
 |
(2.5) |
Both the numerators and denominators of the stabilized weights can be estimated by fitting the corresponding logistic regressions and plugging in the estimated probabilities (Robins, 2000). For presentational simplicity, we do not distinguish between  and
and  for the rest of the article.
for the rest of the article.
When fitting the MSMs, Hernan and others (2002) used a working independent covariance matrix in the weighted GEE. However, when data show a clear correlation pattern, we are interested in whether modeling the correlation structure might increase the estimation efficiency as in ordinary GEE analysis (Zhao and others, 1992). For instance, in AAA, the Pearson correlation coefficient of the hearing measurements between left and right ears is as high as 0.7.
3. MSMs for repeated measurements with multilevel correlation
3.1. Modeling the first and second layer correlation
Similar to the ordinary GEE analysis, various working covariance matrices can be adopted to take account of the correlation between repeated measurements from the same subject for MSM. Take the AAA as an example. The first and second layers of correlation come from each study participant, and a potential working covariance matrix in (2.3) for the repeated hearing measurements for a particular study participant may be:
 |
where the hearing measurements of the left and right ear have the same variance at the same time, but the variance varies as time changes; the correlations between left and right ear are  and
and  , at
, at  and
and  , respectively, and the correlations of hearing measurements across different times are
, respectively, and the correlations of hearing measurements across different times are 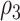 and
and 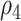 , depending on whether we are comparing the same ear or different ears. Moreover, some commonly used working covariance matrices can also be adopted such as Exchangeable, Autoregressive-1 (AR-1), and unstructured.
, depending on whether we are comparing the same ear or different ears. Moreover, some commonly used working covariance matrices can also be adopted such as Exchangeable, Autoregressive-1 (AR-1), and unstructured.
Different from the ordinary GEE analysis, where the choice of working covariance matrix will not affect the consistency of the parameters being estimated (Zeger and Liang, 1986) when fitting MSMs, we have to be cautious about the working covariance matrix adopted. Tchetgen Tchetgen and others (2012) showed that the estimates with inappropriate weights from weighted GEE could be biased even if we have correctly specified the correlation structure. In order to obtain unbiased estimates of the causal parameters, two options are available. The first option follows from Hernan and others (2002)’s approach by adopting an independent covariance matrix in the weighted GEE, while the element in the weight matrix 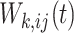 should reflect the inverse treatment probability up to time
should reflect the inverse treatment probability up to time  for the
for the  th unit. The other option is to adopt a nonindependent working covariance matrix; however, in this case,
th unit. The other option is to adopt a nonindependent working covariance matrix; however, in this case, 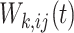 should be the inverse probability of treatment regime throughout the entire follow-up of the block that is considered. To calculate the treatment probability of the entire block, we make the assumption that the treatments between different units are conditionally independent given the units’ covariates and treatment history:
should be the inverse probability of treatment regime throughout the entire follow-up of the block that is considered. To calculate the treatment probability of the entire block, we make the assumption that the treatments between different units are conditionally independent given the units’ covariates and treatment history:
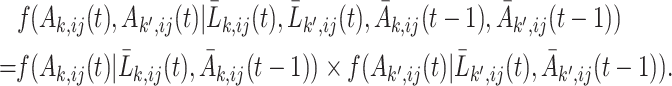 |
Therefore, for the second option, the unstabilized and the stabilized weights in (2.4) and (2.5) should be modified to:
 |
(3.6) |
Note that the weight for unit  of subject
of subject  at time
at time  equals the inverse of the entire treatment probability of subject
equals the inverse of the entire treatment probability of subject  , where the product is taking over all units and time points for this subject.
, where the product is taking over all units and time points for this subject.
However, if the conditional independence of the treatment between units within a subject fails to hold, we can adopt the method proposed by Tchetgen Tchetgen and VanderWeele (2012), where a random-effects model is applied to estimate the unit-level treatment probability and the subject-level treatment probability can be calculated by integrating out the random-effects component. To be specific,
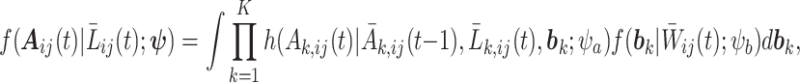 |
where  can be based on the logistic regression model:
can be based on the logistic regression model: 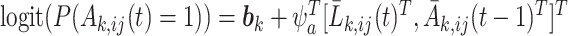 ,
,  is a random effect following a parametric distribution with density function
is a random effect following a parametric distribution with density function  , and
, and  is a subset of
is a subset of  , containing subject-level covariates that are shared by all units in subject
, containing subject-level covariates that are shared by all units in subject  .
.
The unstabilized weights can therefore be modified as:
 |
(3.7) |
and for the stabilized weights, a similar procedure mentioned above can be performed to get the numerator.
3.2. Modeling the third layer correlation
Apart from the correlation between repeated measurements within the same subject  , there also exists a correlation between subjects from the same cluster. For example, in the AAA, subjects that had their hearing tests conducted in the same testing site could be correlated due to some unmeasured cluster-level confounders.
, there also exists a correlation between subjects from the same cluster. For example, in the AAA, subjects that had their hearing tests conducted in the same testing site could be correlated due to some unmeasured cluster-level confounders.
The method described in Section 3.1 can be easily extended to incorporate the additional between-subject correlation, where the estimating equation can be formulated as:
 |
(3.8) |
where  is a column vector containing the repeated measurements for all subjects in the
is a column vector containing the repeated measurements for all subjects in the  th cluster,
th cluster,  is the corresponding vector of expected values of the outcomes,
is the corresponding vector of expected values of the outcomes,  ,
,  is the working covariance matrix reflecting the correlation information within and between subjects from cluster
is the working covariance matrix reflecting the correlation information within and between subjects from cluster  , and
, and  is the weight matrix. In order to get unbiased estimates of the causal parameters, the corresponding weights should reflect the treatment history of the entire cluster. We further make the assumption that the treatments between subjects from the same cluster are conditionally independent given the covariates and treatment history, and therefore the weights can be formulated as:
is the weight matrix. In order to get unbiased estimates of the causal parameters, the corresponding weights should reflect the treatment history of the entire cluster. We further make the assumption that the treatments between subjects from the same cluster are conditionally independent given the covariates and treatment history, and therefore the weights can be formulated as:
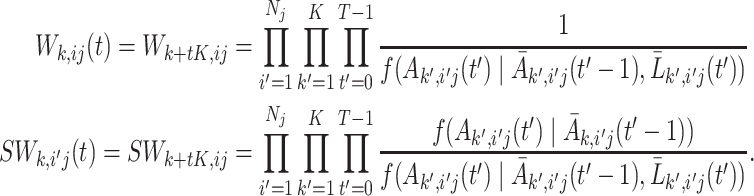 |
(3.9) |
However, directly modeling the correlation between subjects from the whole cluster as described above may result in random violation of positivity (Perterson and others, 2012; Westreich and Cole, 2010), since, to get unbiased estimates of the causal parameters, each element in the weight matrix  should be the inverse probability of the treatment history of the whole cluster
should be the inverse probability of the treatment history of the whole cluster  . In this case, the treatment regime is on the cluster level, and some cluster-level treatment regimes may not be able to be observed due to a finite number of clusters. For instance, if each cluster only has 10 subjects with each subject having two repeated measurements, the treatment of the whole cluster could have
. In this case, the treatment regime is on the cluster level, and some cluster-level treatment regimes may not be able to be observed due to a finite number of clusters. For instance, if each cluster only has 10 subjects with each subject having two repeated measurements, the treatment of the whole cluster could have 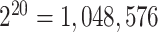 possible different paths and its unrealistic to have data set of over one million clusters such that all treatment paths are observed. Thus, this “random” violation of positivity is almost guaranteed to happen even under moderate cluster sizes.
possible different paths and its unrealistic to have data set of over one million clusters such that all treatment paths are observed. Thus, this “random” violation of positivity is almost guaranteed to happen even under moderate cluster sizes.
We will refer to the method of directly modeling the possible correlations in the data and solving the weighted GEE in 2.3 or 3.8 as the one-stage method hereafter.
To fully exploit the correlation structure, in the next section, we propose a two-stage analysis approach to estimate the causal parameters without violation of positivity while in the meantime, capturing both the within- and between-subject correlations for subjects from the same cluster.
3.3. A two-stage analysis approach to account for between-subject correlation
Before we introduce the two-stage analysis approach, additional assumptions are needed for causal inference.
• Assumption 4
The cluster size is noninformative
The noninformative cluster size assumption states that the outcome of interest is conditionally independent of the number of subjects in the cluster given the subjects’ covariates (Seaman and others, 2014).
• Assumption 5
Random effects under the same treatment path (Wu and others, 2021)
Let  be the average treatment effect comparing treatment regime
be the average treatment effect comparing treatment regime  versus
versus  in cluster
in cluster  , and
, and  with
with  ; that is, the cluster-specific
; that is, the cluster-specific  is a random sample from the population ATE (
is a random sample from the population ATE (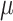 ). Moreover, the estimated cluster-specific
). Moreover, the estimated cluster-specific  is:
is:  , where
, where  is the within-cluster sampling error, and is independent of
is the within-cluster sampling error, and is independent of  .
.
Our causal estimand is the population ATE (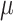 ), and borrowing ideas from the random-effects meta-analysis, it can be estimated through the following two-stage procedure.
), and borrowing ideas from the random-effects meta-analysis, it can be estimated through the following two-stage procedure.
In the first stage, we fit a cluster-specific MSM for each cluster  :
:
 |
(3.10) |
where each cluster has a cluster-specific causal parameters  . The estimating equation can therefore be formulated as:
. The estimating equation can therefore be formulated as:
 |
The first stage cluster-specific MSMs can model the correlation of repeated measurements within the same subject by adopting various forms of working covariance matrices as described in Section 3.1. After obtaining the point estimates of the cluster-specific ATEs and their variances through the sandwich variance estimator, in the second stage, the population ATEs can be estimated by combining the estimates  using mixed-effects meta-analysis with variance-based weighting (Borenstein and others, 2010). For a specific causal parameter
using mixed-effects meta-analysis with variance-based weighting (Borenstein and others, 2010). For a specific causal parameter  , in
, in  , the model can be formulated as:
, the model can be formulated as:
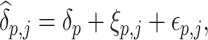 |
(3.11) |
where  and
and  are assumed to be independent, and
are assumed to be independent, and  represents the difference between the population mean (
represents the difference between the population mean ( ) of the causal effect and the true cluster-specific causal effect
) of the causal effect and the true cluster-specific causal effect  in cluster
in cluster 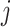 , while
, while  represents the difference between the causal effect of cluster
represents the difference between the causal effect of cluster  and the estimated causal effect
and the estimated causal effect  (Borenstein and others, 2010). From Model (3.11), the overall variance of
(Borenstein and others, 2010). From Model (3.11), the overall variance of 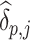 stems from two sources, with
stems from two sources, with  capturing the within-cluster variation while
capturing the within-cluster variation while  containing the between-cluster variation (Borenstein and others, 2010). Therefore, by using mixed-effects meta-analysis, we could implicitly account for the correlation between subjects from the same cluster. Note that, because of Assumption 5, the estimand that the two-stage method is estimating is equal to the estimand that the one-stage method discussed in Sections 3.1 and 3.2 is estimating, which are both population ATEs. Moreover, the consistency of the two-stage method requires the cluster size approaching infinity in order to get consistent estimate of cluster-specific causal parameters, and we will explore the performance of the two-stage method when the cluster size is small, through a simulation study in Section 4.
containing the between-cluster variation (Borenstein and others, 2010). Therefore, by using mixed-effects meta-analysis, we could implicitly account for the correlation between subjects from the same cluster. Note that, because of Assumption 5, the estimand that the two-stage method is estimating is equal to the estimand that the one-stage method discussed in Sections 3.1 and 3.2 is estimating, which are both population ATEs. Moreover, the consistency of the two-stage method requires the cluster size approaching infinity in order to get consistent estimate of cluster-specific causal parameters, and we will explore the performance of the two-stage method when the cluster size is small, through a simulation study in Section 4.
Moreover, the mixed-effects meta-analysis approach described above is conducted for one parameter at a time which ignores the possible correlations between different parameters. Therefore, a multivariate mixed-effects meta-analysis can be considered where the correlations of different causal parameters in the MSMs can be taken into account (Sera and others, 2019). The model can be formulated as follows:
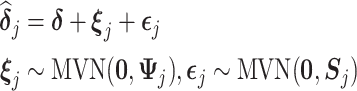 |
where all the causal parameters in the cluster-specific MSMs are analyzed together, and marginally, 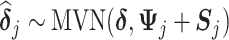 such that different parameters in
such that different parameters in 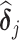 are correlated. Various covariance matrices can be assumed for the random intercepts
are correlated. Various covariance matrices can be assumed for the random intercepts  , such as exchangeable, AR1 and unstructured. An estimate of
, such as exchangeable, AR1 and unstructured. An estimate of  can be obtained using the sandwich variance estimator from the first stage cluster-specific MSMs. The fixed effects parameters
can be obtained using the sandwich variance estimator from the first stage cluster-specific MSMs. The fixed effects parameters  and the covariance matrix of the random effects
and the covariance matrix of the random effects  can be estimated through (restricted) maximum likelihood methods (Sera and others, 2019).
can be estimated through (restricted) maximum likelihood methods (Sera and others, 2019).
3.4. Estimation of the weights
The MSMs adjust for time-dependent confounders  by incorporating them in the model for obtaining the inverse probability of treatment in the weight matrix
by incorporating them in the model for obtaining the inverse probability of treatment in the weight matrix  (Hernan and others, 2002). Therefore, a correctly specified model for the treatment probability is essential to get unbiased estimates of the causal parameters. In this article, we assume that there is no unmeasured confounder on the subject level, but there exists unmeasured cluster-level confounders
(Hernan and others, 2002). Therefore, a correctly specified model for the treatment probability is essential to get unbiased estimates of the causal parameters. In this article, we assume that there is no unmeasured confounder on the subject level, but there exists unmeasured cluster-level confounders  as illustrated in Figure 1. To properly account for the cluster-level unmeasured confounders, we propose the following two approaches to estimating the treatment probabilities.
as illustrated in Figure 1. To properly account for the cluster-level unmeasured confounders, we propose the following two approaches to estimating the treatment probabilities.
The first method is to fit a fixed effects model for the treatment probability by incorporating cluster-specific fixed intercepts:
 |
where the cluster-specific fixed intercept 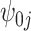 incorporates the information for both the measured and unmeasured cluster-level confounders such that it is robust to model misspecification due to cluster-level confounding (Li and others, 2013). However, the fixed effects method may yield unstable estimates of the treatment probability if the sample sizes of some clusters are so small that
incorporates the information for both the measured and unmeasured cluster-level confounders such that it is robust to model misspecification due to cluster-level confounding (Li and others, 2013). However, the fixed effects method may yield unstable estimates of the treatment probability if the sample sizes of some clusters are so small that  cannot be estimated with high precision. An alternative approach is to use the mixed-effects model:
cannot be estimated with high precision. An alternative approach is to use the mixed-effects model:
 |
where  is the common intercept,
is the common intercept,  is the cluster-specific random intercepts, following the distribution of
is the cluster-specific random intercepts, following the distribution of 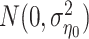 . The distributional assumption on the random effects greatly reduces the number of parameters to be estimated and thus is more stable when the size of cluster is small. However, if the normality assumption of the random effects is violated, the mixed-effects model can result in less precise estimates of the treatment probabilities. Moreover, there may be shrinkage of random effects towards 0 in random-effects model (Li and others, 2013), which would lead to inconsistent estimation of the treatment effects if the sample size per cluster does not increase as the number of clusters increases. Also, if the cluster-specific random effects are correlated with the covariates in the model, the estimated parameters would be biased (Li and others, 2013; Mundlak, 1978). We explore the performance of using both models to estimate the treatment probability in Section 4 when the effects of unmeasured cluster-level confounders on the treatment are generated from different distributions.
. The distributional assumption on the random effects greatly reduces the number of parameters to be estimated and thus is more stable when the size of cluster is small. However, if the normality assumption of the random effects is violated, the mixed-effects model can result in less precise estimates of the treatment probabilities. Moreover, there may be shrinkage of random effects towards 0 in random-effects model (Li and others, 2013), which would lead to inconsistent estimation of the treatment effects if the sample size per cluster does not increase as the number of clusters increases. Also, if the cluster-specific random effects are correlated with the covariates in the model, the estimated parameters would be biased (Li and others, 2013; Mundlak, 1978). We explore the performance of using both models to estimate the treatment probability in Section 4 when the effects of unmeasured cluster-level confounders on the treatment are generated from different distributions.
4. Simulations
4.1. Data generation mechanism
In the simulation study, we explore the performance of our proposed methods on estimating the causal parameters while taking account of the complex correlation structure of data, and compare them with the conventional approach of fitting a weighted GEE using a working independent covariance matrix. Moreover, we study the influence of applying fixed- and mixed-effects models to obtain the treatment probability on the estimation of causal parameters in the presence of unmeasured cluster-level confounders.
The simulation is set up to follow the causal relationships presented in Figure 1, mimicking the data structure in the AAA. We assume there are direct arrows from  (which is contained in
(which is contained in  ) to
) to  , but no direct arrow to
, but no direct arrow to  for computational simplicity of the g-formula which is used to get the true causal parameters in the MSM as shown in Section 3 of the Supplementary material available at Biostatistics online. Lastly, the left and right ears of the same subject have the same exposure value at a particular time (i.e.,
for computational simplicity of the g-formula which is used to get the true causal parameters in the MSM as shown in Section 3 of the Supplementary material available at Biostatistics online. Lastly, the left and right ears of the same subject have the same exposure value at a particular time (i.e.,  ). Section 2.1 of the Supplementary material available at Biostatistics online provides detailed data generation process.
). Section 2.1 of the Supplementary material available at Biostatistics online provides detailed data generation process.
However, the parameters in the data generation mechanism only reflect association but not necessarily causation due to the time-varying confounders. In order to get the induced MSM from the data generation mechanism, we propose to connect the counterfactual outcomes with the factual laws (i.e., conditional distributions of the observed variables) using g-formula (Robins, 1986; Keogh and others, 2021), and we can therefore get the following implied form of MSM for the simulation study:
 |
(4.12) |
where the expression for these causal parameters are provided in Section 2.3 of the Supplementary material available at Biostatistics online.
Note that, the MSM used by Hernan and others (2002):  is a special case of the model (4.12), with
is a special case of the model (4.12), with  . Therefore, model (4.12) can estimate not only the cumulative effect of exposure but also the individual effect of exposure at each time point. We provide the interpretations for
. Therefore, model (4.12) can estimate not only the cumulative effect of exposure but also the individual effect of exposure at each time point. We provide the interpretations for  , and
, and  in Section 5. Mathematical details on the derivation of the induced causal parameters can be found in the Supplementary material available at Biostatistics online.
in Section 5. Mathematical details on the derivation of the induced causal parameters can be found in the Supplementary material available at Biostatistics online.
4.2. Simulation results
Each simulation is conducted 1000 times, with the causal parameters in (4.12) set to be  ,
,  ,
,  ,
,  . We set the number of testing sites at
. We set the number of testing sites at  , with each testing site having tested
, with each testing site having tested  study participants. Several working covariance matrices are considered for the weighted GEE. For the one-stage method, when we only focus on the correlation of the repeated measurements within the same subject, working independent, exchangeable, AR1, and the user-defined matrix
study participants. Several working covariance matrices are considered for the weighted GEE. For the one-stage method, when we only focus on the correlation of the repeated measurements within the same subject, working independent, exchangeable, AR1, and the user-defined matrix
 |
are adopted. The working exchangeable covariance matrix can be regarded as an approximation of the true correlation structure and we further include AR1 working covariance matrix in order to investigate the impact of mis-specification of the working covariance matrix on the finite-sample performance of the estimated parameters. As for the correlation of the hearing measurements across different subjects from the same testing site, we adopt the working exchangeable and AR1 covariance matrix in the weighted GEE for computational simplicity. Moreover, the two-stage method is conducted where, firstly, we fit separate MSMs on each testing site, assuming working exchangeable, AR1 and the user-defined covariance matrix for the repeated measurements from the same subject and then apply the univariate mixed-effects meta-analysis to combine the parameter estimates from all testing sites. The generic inverse variance method is used to combine the estimates (Borenstein and others, 2010), and restricted maximum likelihood is adopted to estimate the between-study variance (Viechtbauer, 2005). Lastly, we try the multivariate mixed-effects meta-analysis approach to combine the cluster-specific parameter estimates using the  package, and the results are similar to those obtained from the univariate mixed-effects meta-analysis approach and are presented in Tables of the Supplementary material available at Biostatistics online.
package, and the results are similar to those obtained from the univariate mixed-effects meta-analysis approach and are presented in Tables of the Supplementary material available at Biostatistics online.
Tables 1 and 2 contain the simulation results for the one-stage method, which models the first two layers of correlations using the working independent or exchangeable covariance matrix, and the two-stage method when the effects of unmeasured cluster-level confounders on the treatment is generated from  . We report the percent bias and empirical standard error (SE) for parameters
. We report the percent bias and empirical standard error (SE) for parameters  , and
, and  over the 1000 simulations. Moreover, for each simulation, we construct the 95
over the 1000 simulations. Moreover, for each simulation, we construct the 95 confidence interval (CI) based on the Sandwich variance estimator of the estimated parameters, and report its coverage probability (CP). More simulation results can be found in Tables S1 and S2 of the Supplementary material available at Biostatistics online.
confidence interval (CI) based on the Sandwich variance estimator of the estimated parameters, and report its coverage probability (CP). More simulation results can be found in Tables S1 and S2 of the Supplementary material available at Biostatistics online.
Table 1.
Average percent bias, empirical SE, and CP of the 95 CI of
CI of  , and
, and  across 1000 simulation replicates
across 1000 simulation replicates
| No. of testing sites | Testing site size | Method |

|

|
|

|
||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias (SE) | CP | Bias (SE) | CP | Bias (SE) | CP | Bias (SE) | CP | |||
| 50 | 30 | IndCov |
 0.2
0.2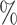 (0.143) (0.143) |
0.949 |
 2.1
2.1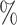 (0.121) (0.121) |
0.989 | 2.2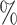 (0.130) (0.130) |
0.990 | 0.1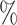 (0.070) (0.070) |
0.950 |
| ExchCov |
 0.1
0.1 (0.140) (0.140) |
0.956 |
 1.7
1.7 (0.079) (0.079) |
0.976 | 1.0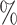 (0.081) (0.081) |
0.981 | 0.1 (0.104) (0.104) |
0.957 | ||
| ExchTwoS | 0.1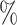 (0.070) (0.070) |
0.947 |
 1.0
1.0 (0.069) (0.069) |
0.954 | 0.3 (0.073) (0.073) |
0.947 | 0.1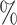 (0.056) (0.056) |
0.947 | ||
| 50 | 60 | IndCov |
 0.3
0.3 (0.099) (0.099) |
0.955 |
 1.2
1.2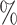 (0.088) (0.088) |
0.993 | 1.0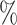 (0.096) (0.096) |
0.992 |
 0.1
0.1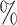 (0.049) (0.049) |
0.949 |
| ExchCov |
 0.3
0.3 (0.094) (0.094) |
0.961 |
 1.2
1.2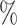 (0.055) (0.055) |
0.978 | 1.0 (0.055) (0.055) |
0.986 |
 0.1
0.1 (0.071) (0.071) |
0.961 | ||
| ExchTwoS |
 0.2
0.2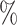 (0.047) (0.047) |
0.949 |
 1.0
1.0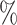 (0.047) (0.047) |
0.948 | 0.7 (0.049) (0.049) |
0.944 |
 0.1
0.1 (0.038) (0.038) |
0.956 | ||
| 100 | 30 | IndCov |
 0.1
0.1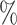 (0.102) (0.102) |
0.963 |
 1.6
1.6 (0.096) (0.096) |
0.986 | 3.1 (0.105) (0.105) |
0.975 | 0.0 (0.049) (0.049) |
0.950 |
| ExchCov | 0.1 (0.097) (0.097) |
0.963 |
 1.1
1.1 (0.061) (0.061) |
0.971 | 1.5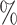 (0.067) (0.067) |
0.963 | 0.4 (0.072) (0.072) |
0.958 | ||
| ExchTwoS |
 0.1
0.1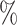 (0.047) (0.047) |
0.960 |
 0.9
0.9 (0.051) (0.051) |
0.947 | 0.8 (0.056) (0.056) |
0.947 | 0.1 (0.040) (0.040) |
0.943 | ||
| 100 | 60 | IndCov | 0.2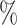 (0.074) (0.074) |
0.964 | 0.5 (0.067) (0.067) |
0.995 |
 0.1
0.1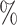 (0.072) (0.072) |
0.996 | 0.1 (0.033) (0.033) |
0.956 |
| ExchCov | 0.1 (0.068) (0.068) |
0.964 |
 0.3
0.3 (0.039) (0.039) |
0.979 | 0.3 (0.041) (0.041) |
0.985 | 0.2 (0.053) (0.053) |
0.961 | ||
| ExchTwoS | 0.0 (0.034) (0.034) |
0.945 |
 0.1
0.1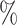 (0.034) (0.034) |
0.953 | 0.1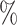 (0.035) (0.035) |
0.964 | 0.1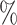 (0.029) (0.029) |
0.952 | ||
A fixed-effects model is used to estimate the treatment probability and the effects of cluster-level unmeasured confounder on the treatment are generated from 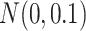 . For the one-stage method, we consider the following situations: (1) using a working independent covariance matrix (IndCov); (2) using a working exchangeable covariance matrix for within-subject correlation and assume independence between subjects (ExchCov). For the two-stage method, we consider using a working exchangeable covariance matrix for the first stage cluster-specific MSMs and combine the results using mixed-effects meta-analysis (ExchTwoS).
. For the one-stage method, we consider the following situations: (1) using a working independent covariance matrix (IndCov); (2) using a working exchangeable covariance matrix for within-subject correlation and assume independence between subjects (ExchCov). For the two-stage method, we consider using a working exchangeable covariance matrix for the first stage cluster-specific MSMs and combine the results using mixed-effects meta-analysis (ExchTwoS).
Table 2.
Average percent bias, empirical SE, and CP of the 95 CI of
CI of 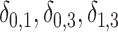 , and
, and  across 1000 simulation replicates
across 1000 simulation replicates
| No. of testing sites | Testing site size | Method |

|

|

|

|
||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias (SE) | CP | Bias (SE) | CP | Bias (SE) | CP | Bias (SE) | CP | |||
| 50 | 30 | IndCov | 0.3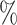 (0.127) (0.127) |
0.963 | 0.9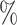 (0.112) (0.112) |
0.997 |
 3.0
3.0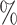 (0.123) (0.123) |
0.996 | 0.1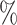 (0.070) (0.070) |
0.952 |
| ExchCov | 0.4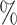 (0.124) (0.124) |
0.957 | 1.5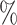 (0.078) (0.078) |
0.955 |
 4.0
4.0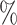 (0.082) (0.082) |
0.949 |
 0.1
0.1 (0.094) (0.094) |
0.956 | ||
| ExchTwoS | 0.3 (0.067) (0.067) |
0.940 |
 0.2
0.2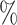 (0.067) (0.067) |
0.951 |
 0.5
0.5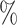 (0.071) (0.071) |
0.952 | 0.2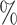 (0.054) (0.054) |
0.947 | ||
| 50 | 60 | IndCov | 0.0 (0.090) (0.090) |
0.968 | 0.6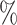 (0.082) (0.082) |
0.994 |
 2.2
2.2 (0.085) (0.085) |
0.997 |
 0.1
0.1 (0.049) (0.049) |
0.950 |
| ExchCov | 0.1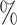 (0.087) (0.087) |
0.961 | 1.8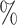 (0.055) (0.055) |
0.958 |
 2.8
2.8 (0.054) (0.054) |
0.958 |
 0.2
0.2 (0.065) (0.065) |
0.960 | ||
| ExchTwoS |
 0.1
0.1 (0.046) (0.046) |
0.949 |
 0.2
0.2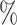 (0.046) (0.046) |
0.949 |
 0.1
0.1 (0.048) (0.048) |
0.945 | 0.0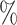 (0.037) (0.037) |
0.960 | ||
| 100 | 30 | IndCov |
 0.3
0.3 (0.089) (0.089) |
0.961 |
 3.3
3.3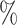 (0.078) (0.078) |
0.980 | 3.6 (0.088) (0.088) |
0.968 | 0.0 (0.049) (0.049) |
0.950 |
| ExchCov | 0.0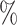 (0.084) (0.084) |
0.965 |
 0.7
0.7 (0.058) (0.058) |
0.960 | 2.2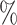 (0.061) (0.061) |
0.942 | 0.3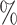 (0.063) (0.063) |
0.962 | ||
| ExchTwoS |
 0.1
0.1 (0.046) (0.046) |
0.963 |
 0.6
0.6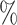 (0.050) (0.050) |
0.947 | 0.9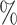 (0.055) (0.055) |
0.945 | 0.1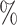 (0.038) (0.038) |
0.946 | ||
| 100 | 60 | IndCov | 0.1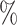 (0.064) (0.064) |
0.970 |
 2.1
2.1 (0.057) (0.057) |
0.990 | 2.4 (0.060) (0.060) |
0.989 | 0.1 (0.034) (0.034) |
0.955 |
| ExchCov | 0.2 (0.059) (0.059) |
0.961 |
 0.3
0.3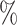 (0.037) (0.037) |
0.966 | 1.5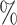 (0.039) (0.039) |
0.965 | 0.4 (0.046) (0.046) |
0.960 | ||
| ExchTwoS | 0.0 (0.033) (0.033) |
0.947 | 0.0 (0.033) (0.033) |
0.953 | 0.0 (0.034) (0.034) |
0.967 | 0.1 (0.028) (0.028) |
0.955 | ||
A mixed-effects model is used to estimate the treatment probability and the effects of cluster-level unmeasured confounder on the treatment are generated from  . For the one-stage method, we consider the following situations: (1) using a working independent covariance matrix (IndCov); (2) using a working exchangeable covariance matrix for within subject correlation and assume independence between subjects (ExchCov). For the two-stage method, we consider using a working exchangeable covariance matrix for the first stage cluster-specific MSMs and combine the results using mixed-effects meta-analysis (ExchTwoS).
. For the one-stage method, we consider the following situations: (1) using a working independent covariance matrix (IndCov); (2) using a working exchangeable covariance matrix for within subject correlation and assume independence between subjects (ExchCov). For the two-stage method, we consider using a working exchangeable covariance matrix for the first stage cluster-specific MSMs and combine the results using mixed-effects meta-analysis (ExchTwoS).
In Table 1 and Table S1 of the Supplementary material available at Biostatistics online, where fixed effects model is applied to estimate the treatment probability, for the one-stage method, adopting the working exchangeable, AR1 and the user-defined covariance matrix to model the within-subject correlation while ignoring the correlation between subjects in the weighted GEE leads to percent biases that are in general less than 1 , while assuming a working independent covariance matrix tend to yield percent biases that are greater than 1
, while assuming a working independent covariance matrix tend to yield percent biases that are greater than 1 . Since the true covariance structure of the data is close to exchangeable, adopting an exchangeable working covariance matrix in general has smaller empirical SEs except for
. Since the true covariance structure of the data is close to exchangeable, adopting an exchangeable working covariance matrix in general has smaller empirical SEs except for  . For instance, for the case when we have 50 testing sites with 30 subjects in each site, the empirical SE of
. For instance, for the case when we have 50 testing sites with 30 subjects in each site, the empirical SE of  decreases from 0.121 by using an independent covariance matrix to 0.079 by using a exchangeable covariance matrix. As shown in Table S1 of the Supplementary material available at Biostatistics online, using the AR1 working covariance matrix typically leads to larger empirical SEs than using the exchangeable or user-defined covariance matrices. Moreover, the coverage probabilities are closer to the 95
decreases from 0.121 by using an independent covariance matrix to 0.079 by using a exchangeable covariance matrix. As shown in Table S1 of the Supplementary material available at Biostatistics online, using the AR1 working covariance matrix typically leads to larger empirical SEs than using the exchangeable or user-defined covariance matrices. Moreover, the coverage probabilities are closer to the 95 nominal level if we use a nonindependent working covariance matrix while using a working independent covariance matrix often yield conservative CIs with coverage probabilities close to 1. The over-coverage of the CIs could be due to the sandwich variance estimator not accounting for the uncertainty in the estimation of the stabilized weights (Robins and others, 2000). Alternatively, bootstrap method can be used in place of the robust sandwich variance estimator to address the over-coverage issue. Moreover, Shu and others (2021) proposed a corrected sandwich variance estimator with the idea of stacking the estimating equations for both the outcome model and the model for estimating the treatment probability. Note that, for the one-stage method, if we further model the correlation between subjects from the same testing site using either the exchangeable or AR1 working covariance matrix, the estimates are biased. This is expected since in the weighted GEE, the weight matrix should reflect the treatment probability of the whole cluster, and when each cluster has 30 or 60 people, a total number of at least
nominal level if we use a nonindependent working covariance matrix while using a working independent covariance matrix often yield conservative CIs with coverage probabilities close to 1. The over-coverage of the CIs could be due to the sandwich variance estimator not accounting for the uncertainty in the estimation of the stabilized weights (Robins and others, 2000). Alternatively, bootstrap method can be used in place of the robust sandwich variance estimator to address the over-coverage issue. Moreover, Shu and others (2021) proposed a corrected sandwich variance estimator with the idea of stacking the estimating equations for both the outcome model and the model for estimating the treatment probability. Note that, for the one-stage method, if we further model the correlation between subjects from the same testing site using either the exchangeable or AR1 working covariance matrix, the estimates are biased. This is expected since in the weighted GEE, the weight matrix should reflect the treatment probability of the whole cluster, and when each cluster has 30 or 60 people, a total number of at least 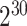 or
or 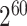 testing sites are needed to avoid positivity violation. Lastly, the two-stage method also yield parameter estimates that are less biased with coverage probabilities even closer to 95
testing sites are needed to avoid positivity violation. Lastly, the two-stage method also yield parameter estimates that are less biased with coverage probabilities even closer to 95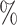 nominal level, and it is interesting to note that the efficiency gain from the two-stage method is even more significant.
nominal level, and it is interesting to note that the efficiency gain from the two-stage method is even more significant.
We observe similar results in Table 2 and Supplementary Table 2, where a mixed-effects model is applied to estimate the treatment probability. Additionally, the empirical SEs of the coefficient estimates are smaller than those estimated using the fixed effects model with reductions ranging from 2 to 25
to 25 . This may be due to the fact that the mixed-effects model has fewer effective number of parameters to estimate compared with the fixed effects model.
. This may be due to the fact that the mixed-effects model has fewer effective number of parameters to estimate compared with the fixed effects model.
We conduct additional simulations by reducing the size of each cluster to be 5 or 10. As shown in Table S9 of the Supplementary material available at Biostatistics online, using fixed effects model to estimate the treatment probability typically leads to substantial bias, probably due to the difficulty in getting precise estimates of the cluster-specific fixed intercepts under the small cluster size. However, using the mixed-effects model to estimate the treatment probability leads to less biased estimates (Table S10 of the Supplementary material available at Biostatistics online). The two-stage method gives more biased estimates than the one-stage method, with the latter directly modeling the within-subject correlation using a working exchangeable covariance matrix (Tables S9 and S10 of the Supplementary material available at Biostatistics online). This might be because the parameter estimates from the cluster-specific MSMs are less precise when cluster size is small. Besides, in the two-stage method, when cluster size is small, the algorithm for fitting the cluster-specific MSMs is less stable, and in our simulation study when cluster size is 5, about 50 of the clusters ran into a rank deficiency issue. Therefore, in the small cluster size setting, we recommend using the mixed-effects model to estimate the treatment probability and applying the one-stage method by modeling the first two layers of (within-subject) correlation using a suitable working covariance matrix in the weighted GEE.
of the clusters ran into a rank deficiency issue. Therefore, in the small cluster size setting, we recommend using the mixed-effects model to estimate the treatment probability and applying the one-stage method by modeling the first two layers of (within-subject) correlation using a suitable working covariance matrix in the weighted GEE.
In Tables 3 and 4 and Tables S3 and S4 of the Supplementary material available at Biostatistics online, we generate the unmeasured cluster-level confounder effects based on a skewed normal distribution with location parameter set to  1, scale parameter set to 0.1, and shape parameter equal to 100, which corresponds to a highly right-skewed distribution. Since the fixed effects model does not make any distributional assumptions on the unmeasured cluster-level confounder effects, we draw similar conclusions as those from Table 1, where the one-stage method by directly modeling the correlation of the repeated measurements within-subject results in less biased estimates with smaller empirical SEs, while taking a step further to model the correlation of measurements between subjects will lead to biased estimates due to the violation of positivity. In addition, the two-stage method also leads to less biased and more efficient parameter estimates. However, when the mixed-effects model is employed to estimate the treatment probability as shown in Table 4 and Table S4 of the Supplementary material available at Biostatistics online, the estimates have larger bias due to the violation of the normality assumption of the random effects. Therefore, using fixed effects model to estimate the treatment probability is preferred when the effects of unmeasured cluster-level confounders may not be normally distributed and the sample size of each cluster is large. Otherwise, mixed-effects model is recommended especially when the clusters have small sample sizes.
1, scale parameter set to 0.1, and shape parameter equal to 100, which corresponds to a highly right-skewed distribution. Since the fixed effects model does not make any distributional assumptions on the unmeasured cluster-level confounder effects, we draw similar conclusions as those from Table 1, where the one-stage method by directly modeling the correlation of the repeated measurements within-subject results in less biased estimates with smaller empirical SEs, while taking a step further to model the correlation of measurements between subjects will lead to biased estimates due to the violation of positivity. In addition, the two-stage method also leads to less biased and more efficient parameter estimates. However, when the mixed-effects model is employed to estimate the treatment probability as shown in Table 4 and Table S4 of the Supplementary material available at Biostatistics online, the estimates have larger bias due to the violation of the normality assumption of the random effects. Therefore, using fixed effects model to estimate the treatment probability is preferred when the effects of unmeasured cluster-level confounders may not be normally distributed and the sample size of each cluster is large. Otherwise, mixed-effects model is recommended especially when the clusters have small sample sizes.
Table 3.
Average percent bias, empirical SE, and CP of the 95 CI of
CI of  , and
, and  across 1000 simulation replicates
across 1000 simulation replicates
| No. of testing sites | Testing site size | Method |

|

|

|

|
||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias (SE) | CP | Bias (SE) | CP | Bias (SE) | CP | Bias (SE) | CP | |||
| 50 | 30 | IndCov |
 0.3
0.3 (0.153) (0.153) |
0.938 |
 1.7
1.7 (0.133) (0.133) |
0.992 | 3.4 (0.152) (0.152) |
0.978 |
 0.1
0.1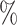 (0.070) (0.070) |
0.955 |
| ExchCov |
 0.1
0.1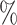 (0.146) (0.146) |
0.954 |
 1.6
1.6 (0.078) (0.078) |
0.973 | 1.9 (0.086) (0.086) |
0.969 | 0.2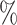 (0.110) (0.110) |
0.956 | ||
| ExchTwoS |
 0.2
0.2 (0.068) (0.068) |
0.947 | 0.9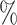 (0.069) (0.069) |
0.944 | 0.3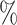 (0.077) (0.077) |
0.941 | 0.0 (0.056) (0.056) |
0.943 | ||
| 50 | 60 | IndCov |
 0.2
0.2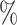 (0.101) (0.101) |
0.968 |
 1.4
1.4 (0.091) (0.091) |
0.997 | 1.4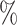 (0.103) (0.103) |
0.985 | 0.0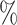 (0.051) (0.051) |
0.949 |
| ExchCov |
 0.1
0.1 (0.099) (0.099) |
0.960 |
 1.2
1.2 (0.059) (0.059) |
0.970 | 1.3 (0.061) (0.061) |
0.978 | 0.1 (0.078) (0.078) |
0.954 | ||
| ExchTwoS |
 0.1
0.1 (0.046) (0.046) |
0.956 |
 0.5
0.5 (0.046) (0.046) |
0.956 | 0.9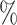 (0.051) (0.051) |
0.941 |
 0.1
0.1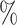 (0.041) (0.041) |
0.944 | ||
| 100 | 30 | IndCov |
 0.1
0.1 (0.101) (0.101) |
0.948 |
 1.8
1.8 (0.095) (0.095) |
0.988 | 3.5 (0.105) (0.105) |
0.965 | 0.1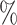 (0.048) (0.048) |
0.949 |
| ExchCov | 0.0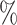 (0.096) (0.096) |
0.959 |
 1.7
1.7 (0.057) (0.057) |
0.972 | 1.9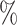 (0.065) (0.065) |
0.963 | 0.4 (0.073) (0.073) |
0.968 | ||
| ExchTwoS |
 0.1
0.1 (0.048) (0.048) |
0.960 |
 1.0
1.0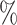 (0.053) (0.053) |
0.948 | 0.9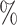 (0.056) (0.056) |
0.936 | 0.2 (0.038) (0.038) |
0.957 | ||
| 100 | 60 | IndCov |
 0.1
0.1 (0.073) (0.073) |
0.961 |
 0.5
0.5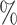 (0.072) (0.072) |
0.991 | 0.5 (0.079) (0.079) |
0.988 | 0.0 (0.034) (0.034) |
0.938 |
| ExchCov |
 0.2
0.2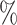 (0.078) (0.078) |
0.959 |
 1.1
1.1 (0.045) (0.045) |
0.970 | 0.8 (0.048) (0.048) |
0.979 | 0.0 (0.062) (0.062) |
0.966 | ||
| ExchTwoS |
 0.2
0.2 (0.034) (0.034) |
0.942 |
 0.7
0.7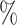 (0.036) (0.036) |
0.945 | 0.6 (0.036) (0.036) |
0.951 | 0.0 (0.028) (0.028) |
0.948 | ||
A fixed-effects model is used to estimate the treatment probability and the effects of cluster-level unmeasured confounder on the treatment are generated from a skewed normal distribution with location parameter to be  1, scale parameter being 0.1 and shape parameter equals to 100. For the one-stage method, we consider the following situations: (1) using a working independent covariance matrix (IndCov); (2) using a working exchangeable covariance matrix for within subject correlation and assume independence between subjects (ExchCov). For the two-stage method, we consider using a working exchangeable covariance matrix for the first stage cluster-specific MSMs and combine the results using mixed-effects meta-analysis (ExchTwoS).
1, scale parameter being 0.1 and shape parameter equals to 100. For the one-stage method, we consider the following situations: (1) using a working independent covariance matrix (IndCov); (2) using a working exchangeable covariance matrix for within subject correlation and assume independence between subjects (ExchCov). For the two-stage method, we consider using a working exchangeable covariance matrix for the first stage cluster-specific MSMs and combine the results using mixed-effects meta-analysis (ExchTwoS).
Table 4.
Average percent bias, empirical SE, and CP of the 95 CI of
CI of  , and
, and  across 1000 simulation replicates
across 1000 simulation replicates
| No. of testing sites | Testing site size | Method |

|

|

|

|
||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias (SE) | CP | Bias (SE) | CP | Bias (SE) | CP | Bias (SE) | CP | |||
| 50 | 30 | IndCov | 0.2 (0.134) (0.134) |
0.964 | 0.8 (0.110) (0.110) |
0.992 | 3.9 (0.124) (0.124) |
0.976 | 0.0 (0.071) (0.071) |
0.952 |
| ExchCov | 0.6 (0.125) (0.125) |
0.958 | 2.5 (0.075) (0.075) |
0.971 | 1.1 (0.085) (0.085) |
0.952 | 0.4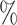 (0.094) (0.094) |
0.958 | ||
| ExchTwoS |
 0.1
0.1 (0.066) (0.066) |
0.949 |
 0.1
0.1 (0.067) (0.067) |
0.944 | 0.4 (0.075) (0.075) |
0.938 | 0.1 (0.053) (0.053) |
0.945 | ||
| 50 | 60 | IndCov | 0.1 (0.088) (0.088) |
0.965 |
 0.7
0.7 (0.077) (0.077) |
0.991 | 4.1 (0.087) (0.087) |
0.980 | 0.0 (0.051) (0.051) |
0.950 |
| ExchCov | 0.5 (0.085) (0.085) |
0.958 | 1.5 (0.055) (0.055) |
0.961 | 1.3 (0.057) (0.057) |
0.966 | 0.3 (0.067) (0.067) |
0.955 | ||
| ExchTwoS | 0.1 (0.045) (0.045) |
0.955 | 0.1 (0.045) (0.045) |
0.956 | 0.8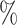 (0.050) (0.050) |
0.939 | 0.0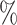 (0.039) (0.039) |
0.946 | ||
| 100 | 30 | IndCov |
 0.5
0.5 (0.089) (0.089) |
0.937 |
 5.0
5.0 (0.079) (0.079) |
0.983 | 4.2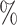 (0.086) (0.086) |
0.967 | 0.1 (0.048) (0.048) |
0.948 |
| ExchCov |
 0.2
0.2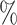 (0.082) (0.082) |
0.949 |
 3.6
3.6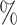 (0.056) (0.056) |
0.958 | 2.2 (0.059) (0.059) |
0.945 | 0.3 (0.063) (0.063) |
0.957 | ||
| ExchTwoS |
 0.1
0.1 (0.046) (0.046) |
0.959 |
 1.2
1.2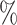 (0.051) (0.051) |
0.952 | 0.8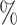 (0.055) (0.055) |
0.940 | 0.2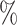 (0.037) (0.037) |
0.961 | ||
| 100 | 60 | IndCov |
 0.4
0.4 (0.059) (0.059) |
0.953 |
 5.1
5.1 (0.052) (0.052) |
0.978 | 3.8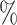 (0.056) (0.056) |
0.969 | 0.1 (0.035) (0.035) |
0.939 |
| ExchCov |
 0.1
0.1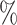 (0.057) (0.057) |
0.954 |
 3.2
3.2 (0.039) (0.039) |
0.941 | 1.8 (0.040) (0.040) |
0.953 | 0.2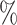 (0.045) (0.045) |
0.956 | ||
| ExchTwoS |
 0.2
0.2 (0.033) (0.033) |
0.948 |
 0.9
0.9 (0.034) (0.034) |
0.940 | 0.4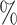 (0.035) (0.035) |
0.955 | 0.0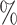 (0.027) (0.027) |
0.950 | ||
A mixed-effects model is used to estimate the treatment probability and the effects of cluster-level unmeasured confounder on the treatment are generated from a skewed normal distribution with location parameter to be  1, scale parameter being 0.1 and shape parameter equals to 100. For the one-stage method, we consider the following situations: (1) using a working independent covariance matrix (IndCov); (2) using a working exchangeable covariance matrix for within subject correlation and assume independence between subjects (ExchCov). For the two-stage method, we consider using a working exchangeable covariance matrix for the first stage cluster-specific MSMs and combine the results using mixed-effects meta-analysis (ExchTwoS).
1, scale parameter being 0.1 and shape parameter equals to 100. For the one-stage method, we consider the following situations: (1) using a working independent covariance matrix (IndCov); (2) using a working exchangeable covariance matrix for within subject correlation and assume independence between subjects (ExchCov). For the two-stage method, we consider using a working exchangeable covariance matrix for the first stage cluster-specific MSMs and combine the results using mixed-effects meta-analysis (ExchTwoS).
5. Illustrative data example
We apply the methods to investigate the causal effects of risk factors for hearing loss in the AAA. We focus on the impact of aspirin use, defined as people who either took regular dose of aspirin or baby aspirin, on the hearing threshold, and we choose the hearing measurements at 4000 Hz as the outcome. There was a total of 3134 patients with hearing tests completed at the baseline and end of the 3-year follow-up. The sample size in the 34 testing sites ranged from 5 to 211. Potential confounders that we control for includes smoking status, weight, race, Ibuprofen usage, age, and body mass index (BMI). Some people had their hearing tests conducted at two different locations at the baseline and end of the AAA. We therefore define the testing sites in the analysis as a categorical variable cross-classified by the testing sites at the start and end of the AAA. For instance, a person may have their hearing test conducted at site A at the baseline but at site B at the end of follow-up, and in this case, we treat them as if they had come from another testing set called AB.
We assume the same form of MSM as in the simulation study for the hearing measurements:
 |
The coefficients can be interpreted as follows:  represents the effect on the hearing threshold at
represents the effect on the hearing threshold at  (baseline of AAA) of taking aspirin at
(baseline of AAA) of taking aspirin at  (last visit before the start of AAA);
(last visit before the start of AAA);  represents the effect on the hearing threshold at
represents the effect on the hearing threshold at  (end of AAA) for people who took aspirin at
(end of AAA) for people who took aspirin at  versus those who did not take aspirin, holding the exposures at
versus those who did not take aspirin, holding the exposures at  and
and 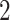 the same;
the same;  represents the effect on the hearing threshold at the end of AAA for people who took aspirin at
represents the effect on the hearing threshold at the end of AAA for people who took aspirin at  versus those who did not take aspirin, while they received the same exposures at
versus those who did not take aspirin, while they received the same exposures at  and
and  ; and
; and  represents the effect on the hearing threshold at the end of follow-up for people who took aspirin at
represents the effect on the hearing threshold at the end of follow-up for people who took aspirin at 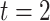 versus those who did not take aspirin, while they had the same exposure at
versus those who did not take aspirin, while they had the same exposure at 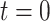 and
and  . Moreover,
. Moreover,  represents the cumulative causal effect of aspirin usage on hearing threshold comparing people who took aspirin at all the prebaseline, baseline, and postbaseline time points versus those who did not take aspirin at any of these time points.
represents the cumulative causal effect of aspirin usage on hearing threshold comparing people who took aspirin at all the prebaseline, baseline, and postbaseline time points versus those who did not take aspirin at any of these time points.
To get the stabilized weight matrix for the weighted GEE, we apply the mixed-effects model to estimate the exposure probability since some testing sites had small number of patients. We assume random-effects logistic regression models for the exposure probability at 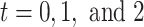 with previous hearing measurements, aspirin use, weight, smoking, age, BMI, and ibuprofen as covariates with all covariates taken from the most recent questionnaire. In addition, three random-effects logistic regression models are fitted with past aspirin use as covariates to obtain the numerators of the stabilized weights.
with previous hearing measurements, aspirin use, weight, smoking, age, BMI, and ibuprofen as covariates with all covariates taken from the most recent questionnaire. In addition, three random-effects logistic regression models are fitted with past aspirin use as covariates to obtain the numerators of the stabilized weights.
Lastly, we assume the following possible working covariance matrices for the repeated hearing measurements within individuals: independent, exchangeable, and four user-defined working covariance matrices listed in Section 5 of the Supplementary material available at Biostatistics online.
Table 5 contains the analysis results. In general, we obtain similar estimates of the coefficients for each working correlation matrices. There is insufficient statistical evidence to conclude that the aspirin use at each time point causally affects the hearing threshold.
Table 5.
MSM for the causal effects of aspirin use on the hearing loss at 4000 Hz
| Method |

|

|

|

|

|

|
|---|---|---|---|---|---|---|
| IndCov | 16.609 (0.227) | 1.317 (0.059) | 0.076 (1.312) |
 0.592 (1.389)
0.592 (1.389) |
0.541 (1.418) | 0.233 (0.880) |
| ExchCov | 16.642 (0.228) | 1.306 (0.055) | 0.087 (1.045) |
 0.424 (0.61)
0.424 (0.61) |
0.335 (0.723) |
 0.282 (0.918)
0.282 (0.918) |
 Cov
Cov |
16.642 (0.228) | 1.306 (0.054) | 0.088 (1.036) |
 0.409 (0.581)
0.409 (0.581) |
0.316 (0.702) |
 0.282 (0.918)
0.282 (0.918) |
 Cov
Cov |
16.642 (0.228) | 1.306 (0.055) | 0.088 (1.04) |
 0.416 (0.594)
0.416 (0.594) |
0.325 (0.711) |
 0.282 (0.918)
0.282 (0.918) |
 Cov
Cov |
16.642 (0.228) | 1.306 (0.054) | 0.088 (1.036) |
 0.409 (0.581)
0.409 (0.581) |
0.316 (0.702) |
 0.282 (0.918)
0.282 (0.918) |
 Cov
Cov |
16.642 (0.228) | 1.306 (0.055) | 0.088 (1.04) |
 0.416 (0.594)
0.416 (0.594) |
0.325 (0.711) |
 0.282 (0.918)
0.282 (0.918) |
| ExchTwoS | 16.714 (0.42) | 1.358 (0.134) | 0.189 (1.401) |
 1.37 (1.183)
1.37 (1.183) |
1.321 (1.684) |
 0.665 (1.177)
0.665 (1.177) |
 TwoS
TwoS |
16.716 (0.419) | 1.357 (0.134) | 0.09 (1.385) |
 1.204 (1.281)
1.204 (1.281) |
1.217 (1.729) |
 0.665 (1.177)
0.665 (1.177) |
 TwoS
TwoS |
16.715 (0.419) | 1.357 (0.134) | 0.171 (1.389) |
 1.417 (1.305)
1.417 (1.305) |
1.336 (1.724) |
 0.665 (1.177)
0.665 (1.177) |
 TwoS
TwoS |
16.716 (0.419) | 1.357 (0.134) | 0.09 (1.385) |
 1.204 (1.281)
1.204 (1.281) |
1.217 (1.729) |
 0.665 (1.177)
0.665 (1.177) |
 TwoS
TwoS |
16.715 (0.419) | 1.357 (0.134) | 0.171 (1.389) |
 1.417 (1.305)
1.417 (1.305) |
1.336 (1.724) |
 0.665 (1.177)
0.665 (1.177) |
A mixed-effects model was is to estimate the treatment probability for the weight matrix. For the one-stage method, we consider the following situations: (1) using a working independent covariance matrix (IndCov); (2) using a working exchangeable covariance matrix for within subject correlation and assume independence between subjects (ExchCov); (3) using the four user-defined covariance matrices for within-subject correlation and assume independence between subjects ( Cov,
Cov,  Cov,
Cov,  Cov,
Cov,  Cov). For the two-stage method, we consider the following situations: (1) using a working exchangeable covariance matrix for the first stage cluster-specific MSMs and combine the results using mixed-effects meta-analysis (ExchTwoS); (2) using the four user-defined covariance matrices for the first stage cluster-specific MSMs and combine the results using mixed-effects meta-analysis (
Cov). For the two-stage method, we consider the following situations: (1) using a working exchangeable covariance matrix for the first stage cluster-specific MSMs and combine the results using mixed-effects meta-analysis (ExchTwoS); (2) using the four user-defined covariance matrices for the first stage cluster-specific MSMs and combine the results using mixed-effects meta-analysis ( TwoS,
TwoS,  TwoS,
TwoS,  TwoS,
TwoS,  TwoS).
TwoS).
Moreover, we can get the cumulative effect of aspirin usage on the hearing measurements at the end of the AAA, with point estimate being  and the estimated SE can be obtained based on the variance–covariance matrix of
and the estimated SE can be obtained based on the variance–covariance matrix of  . Using the results from the MSM assuming a working exchangeable covariance matrix while assuming independence between subjects (second row in the table), we obtain the point estimate of
. Using the results from the MSM assuming a working exchangeable covariance matrix while assuming independence between subjects (second row in the table), we obtain the point estimate of  0.0021 (95
0.0021 (95 CI
CI  1.9341 to 1.9300) for the cumulative treatment effect of aspirin usage on the hearing measurements at the end of AAA. Therefore, there is no statistical evidence of the effect of aspirin use on hearing ability at 4000 Hz in the short term.
1.9341 to 1.9300) for the cumulative treatment effect of aspirin usage on the hearing measurements at the end of AAA. Therefore, there is no statistical evidence of the effect of aspirin use on hearing ability at 4000 Hz in the short term.
6. Discussion
In this article, we propose methods for incorporating the multilevel correlation structure of data when fitting MSMs to estimate the causal effects of time-varying treatment under time-dependent confounders. The first one-stage method models the correlation structures directly by using the corresponding working covariance matrix in the weighted GEE on all individuals across clusters, and the second two-stage analysis approach fits separate MSMs on each cluster first and combines the coefficient estimates using mixed-effects meta-analysis.
Several conclusions can be drawn from our work. Firstly, the one-stage method by modeling the first two layers of correlation structure can result in efficiency gain compared with the approach of assuming an independent structure between repeated measurements. However, if we further model the third layer of correlation, since the weight matrix in the weighted GEE has to reflect the inverse treatment probability of the whole cluster, where the number of possible treatment paths on the cluster level can easily reach an unrealistic large number, violations of positivity are almost guaranteed to occur for any reasonable number of clusters when the cluster size is moderate or larger. The violations of positivity may cause the estimates to be biased. Under such circumstances, we recommend using the two-stage analysis approach, where we fit separate MSMs for each cluster first where some working covariance matrices can be assumed for the correlation of the repeated measurements within subjects, and in the second stage, we use mixed-effects meta-analysis to combine the parameter estimates. Moreover, in the presence of unmeasured cluster-level confounders, we explore both fixed- and mixed-effects model to estimate the treatment probability, where the fixed-effects model accounts for the cluster-level confounders by including cluster-specific fixed intercepts while the mixed-effects model adds cluster-specific random intercepts following a normal distribution. Although the fixed-effects model does not require distributional assumptions for the true unmeasured cluster-level confounder effects, under small cluster size, the fixed-effects model may give less stable estimates of treatment probability, rendering less reliable parameter estimates of the MSMs. Mixed-effects model may be preferred in situations where cluster size is small.
Our two-stage mixed-effects meta-analysis method requires each cluster to be large such that the first-stage cluster-specific MSMs can yield reliable estimates of the causal parameters. In real applications, however, some clusters may have small sample sizes and one way to fully utilize data while obtaining reliable parameter estimates is to collapse those small clusters and run a single MSM on the collapsed clusters.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Contributor Information
Yujie Wu, Department of Biostatistics, Harvard T.H. Chan School of Public Health, Boston, MA 02215, USA.
Benjamin Langworthy, Department of Biostatistics, Harvard T.H. Chan School of Public Health, Boston, MA 02215, USA and Department of Epidemiology, Harvard T.H. Chan School of Public Health, Boston, MA 02215, USA.
Molin Wang, Department of Biostatistics, Harvard T.H. Chan School of Public Health, Boston, MA 02215, USA, Department of Epidemiology, Harvard T.H. Chan School of Public Health, Boston, MA 02215, USA, and Channing Division of Network Medicine, Department of Medicine, Brigham and Women’s Hospital, Boston, MA, 02215, USA and Harvard Medical School, Boston, MA 02115, USA.
7. Software
We provide the code for simulation and real data analysis in the Github repository at https://github.com/YujieWuu/Multi-level_MSM.
Supplementary material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
The National Institute Health (R01 DC017717, U01 CA176726 (NHS II) and U01 HL145386 (NHS II)), in part.
References
- Borenstein, M., Hedges, L. V., Higgins, J. P. T. and Rothstein, H. R. (2010). A basic introduction to fixed-effect and random-effects models for meta-analysis. Research Synthesis Methods 1, 97–111. [DOI] [PubMed] [Google Scholar]
- Curhan, S. G., Wang, M., Eavey, R. D., Stampfer, M. J. and Curhan, G. C. (2018). Adherence to healthful dietary patterns is associated with lower risk of hearing loss in women. The Journal of Nutrition 148, 944–951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curhan, S. G., Halpin, C., Wang, M., Eavey, R. D. and Curhan, G. C. (2020). Prospective study of dietary patterns and hearing threshold elevation. American Journal of Epidemiology 189, 204–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernan, M. A., Brumback, B. A.Robins, J. M. (2002). Estimating the causal effect of zidovudine on CD4 count with a marginal structural model for repeated measures. Statistics in Medicine 21, 1689–1709. [DOI] [PubMed] [Google Scholar]
- Imbens, G. W. and Rubin, D. B. (2015). Causal Inference in Statistics, Social, and Biomedical Sciences. New York, USA: Cambridge University Press. [Google Scholar]
- Keogh, R. H. and Seaman, S. R., Gran, J. M. and Vansteelandt, S. (2021). Simulating longitudinal data from marginal structural models using the additive hazard model. Biometrical Journal 63, 1526–1541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, F., Zaslavsky, A. M. and Landrum, M. B. (2013). Propensity score weighting with multilevel data. Statistics in Medicine 32, 3373–3387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mundlak, Y. (1978). On the pooling of time series and cross section data. Econometrica: Journal of the Econometric Society 46, 69–85. [Google Scholar]
- Petersen, M. L., Porter, K. E., Gruber, S., Wang, Y. and Van Der Laan, M. J (2012). Diagnosing and responding to violations in the positivity assumption. Statistical Methods in Medical Research 21, 31–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prentice, R. L. and Zhao, L. P. (1991). Estimating equations for parameters in means and covariances of multivariate discrete and continuous responses. Biometrics 47, 825–839. [PubMed] [Google Scholar]
- Robins, J. (1986). A new approach to causal inference in mortality studies with a sustained exposure period—application to control of the healthy worker survivor effect. Mathematical Modelling 7, 1393–1512. [Google Scholar]
- Robins, J. M. (2000). Marginal structural models versus structural nested models as tools for causal inference. In: Halloran M.E. and Berry D. (eds), Statistical Models in Epidemiology, the Environment, and Clinical Trials. New York, NY: Springer, pp. 95–133. [Google Scholar]
- Robins, J. M., Hernan, M. A. and Brumback, B. (2000). Marginal structural models and causal inference in epidemiology. Epidemiology 11, 550–560. [DOI] [PubMed] [Google Scholar]
- Seaman, S., Pavlou, M. and Copas, A. (2014). Review of methods for handling confounding by cluster and informative cluster size in clustered data. Statistics in Medicine 33, 5371–5387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sera, F., Armstrong, B., Blangiardo, M. and Gasparrini, A. (2019). An extended mixed-effects framework for meta-analysis. Statistics in Medicine 38, 5429–5444. [DOI] [PubMed] [Google Scholar]
- Shu, D., Young, J. G., Toh, S. and Wang, R. (2021). Variance estimation in inverse probability weighted Cox models. Biometrics 77, 1101–1117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen, E. J. and VanderWeele, T. J. (2012). On causal inference in the presence of interference. Statistical Methods in Medical Research 21, 55–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen, E. J., Glymour, M. M., Weuve, J. and Robins, J. (2012). Specifying the correlation structure in inverse-probability-weighting estimation for repeated measures. Epidemiology 23, 644–646. [DOI] [PubMed] [Google Scholar]
- VanderWeele, T. J., Jackson, J. W. and Li, S. (2016). Causal inference and longitudinal data: a case study of religion and mental health. Social Psychiatry and Psychiatric Epidemiology 51, 1457–1466. [DOI] [PubMed] [Google Scholar]
- Viechtbauer, W. (2005). Bias and efficiency of meta-analytic variance estimators in the random-effects model. Journal of Educational and Behavioral Statistics 30, 261–293. [Google Scholar]
- Westreich, D. and Cole, S. R. (2010). Invited commentary: positivity in practice. American Journal of Epidemiology 171, 674–677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, X., Weinberger, K. R., Wellenius, G. A., Dominici, F. and Braun, D. (2021). Assessing the causal effects of a stochastic intervention in time series data: are heat alerts effective in preventing deaths and hospitalizations? arXiv preprint arXiv:2102.10478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeger, S. L. and Liang, K.-Y. (1986). Longitudinal data analysis for discrete and continuous outcomes. Biometrics 42, 121–130. [PubMed] [Google Scholar]
- Zhao, L. P., Prentice, R. L. and Self, S. G. (1992). Multivariate mean parameter estimation by using a partly exponential model. Journal of the Royal Statistical Society: Series B (Methodological) 54, 805–811. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



