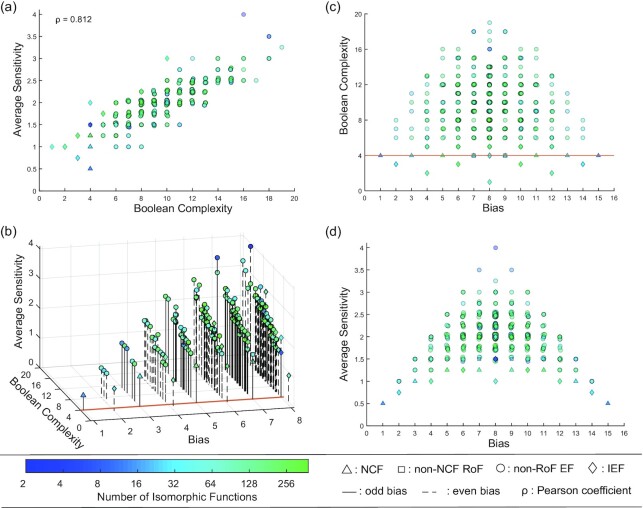
Fig. 3.
Dependence of the 2 complexity measures on the bias and associated 2D projections for all BFs with k = 4 inputs. In each subfigure, a point corresponds to a class of (isomorphic) BF and is assigned a shape and a color. The shape of a point (triangle, square, circle, or diamond) denotes the type of BF (NCF, non-NCF RoF, non-ROF EF, or IEF) whereas its color indicates the number of BFs contained in it’s corresponding class. The same shape and color scheme is applicable to all the plots. A slight ‘jiggle’ is added at some points to resolve overlapping representative BFs. In this plot, the type ‘non-RoF EF’ refers to the subset of EFs which are not RoFs. (a) The linear correlation between the Boolean complexity and the average sensitivity is large and positive. The Pearson correlation coefficient (ρ) between the 2 measures was calculated for all BFs with k = 4 and P ≤ 8. (b) The 3D plot adds the third dimension of bias P to the preceding 2D plot. The solid and dashed vertical lines or ‘needles’, as we will refer to them henceforth, show the projections of the points onto the plane of bias and Boolean complexity. These needles have been included to enhance clarity while distinguishing between the odd bias BFs and even bias BFs. The brown line drawn at the Boolean complexity 4 highlights the functions that possess the minimum Boolean complexity and are effective as well. The RoFs are the only functions which lie along this line. Since the 2 complexity measures are invariant under complementation of the BF, the bias values have been shown only up to P = 8. (c) Variation of the Boolean complexity with the bias. With increasing bias upto P = 8, the number of representative BFs increases, but so does the range of Boolean complexity of these functions. The RoFs and ineffective functions (IEFs) have the minimum Boolean complexity in any 4[P] set. The brown line drawn at the Boolean complexity 4 highlights the functions that possess the minimum Boolean complexity and are effective as well. (d) Variation of average sensitivity with increasing bias. Clearly, the NCFs and IEFs have the minimum average sensitivity in any 4[P] set. Note that both subfigures (c) and (d) are symmetric about P = 8 due to the complementarity property.