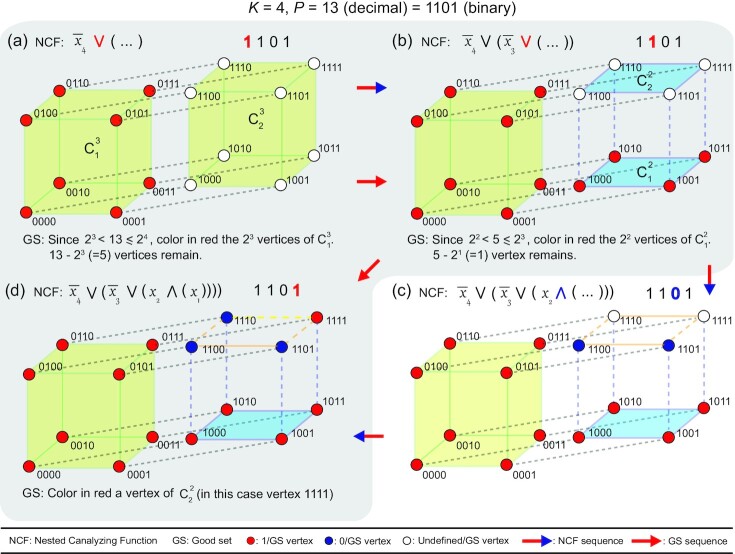
Fig. 4.
A ‘Good set’ (GS) with P vertices where P is odd on a k-dimensional hypercube is equivalent to a NCF in k[P]. In parts (a), (b), and (d) shaded in grey, we show the recursive construction of a GS for P = 13 vertices in a 4D hypercube by coloring it’s vertices red, and in parts (a), (b), (c), and (d), we show the equivalence of that GS with 13 vertices to a NCF with bias 13. The vertices of the hypercube are labeled in the order x4, x3, x2, x1, wherein xi is 0 or 1. Here,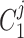 
and 
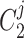denote the 2 vertex disjoint j-dimensional hypercubes of the (j + 1)-dimensional hypercube. The ‘active’ bit in each part (a), (b), (c), and (d) is the colored bit in the binary representation of 13 in that part. (a) Since P = 13 lies between 23 and 24, 23 vertices of either 
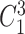or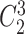 
(here, 
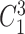) form part of the GS. This leaves 13 − 8 = 5 vertices to be colored red to complete the GS. This choice of 8 vertices in 
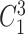for the GS leads to the canalyzation of vertices labeled x4 = 0 to the output value 1. In this step, the active bit is 1 and as a result the ∨ operator follows the literal 
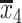. (b) Following the same procedure as in (a) for coloring the remaining 5 vertices of the GS leads to the choice of 4 vertices in 
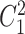. This leaves 1 vertex to be colored (which is the base case of the recursion to construct the GS). The choice of 4 vertices for the GS leads to the canalyzation of vertices with x4 = 1 and x3 = 0 to the output value 1. The active bit in this step is 1 and as a result the ∨ operator follows the literal 
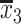. (c) For the corresponding NCF, the vertices with x4 = 1, x3 = 1 and x2 = 0 are canalyzed to the output value 0. The active bit in this step is 0 and as a result the ∧ operator follows the literal x2. (d) For the last step, any vertex in 
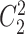can be colored to complete the 13 vertices in GS, and we color here the vertex 1111. The vertex with x4 = 1, x3 = 1, x2 = 1, and x1 = 1 is canalyzed to the output value 1, and the remaining vertex is set to output value 0.