FIGURE 4.

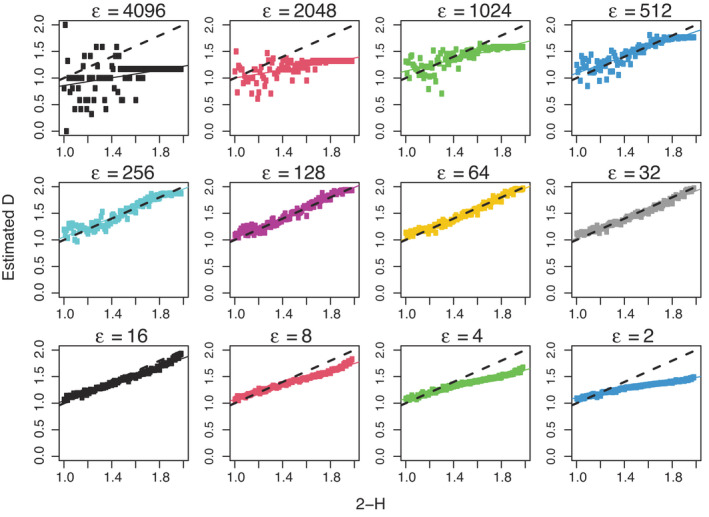
Results of an empirical investigation of the box‐counting algorithm to estimate fractal dimension ($D$). We generated two‐dimensional binary maps of dimension 4097 × 4097 from a midpoint‐displacement algorithm with values of 𝐻 ranging from 0.01 to 0.99. The horizontal axes show the true fractal dimension $D=2-H$, where 𝐻 is the Hurst exponent in the midpoint‐displacement algorithm; the vertical axes show the box‐counting estimate of 𝐷 at each box size 𝜖 (panels); the dashed line on each panel is the one‐to‐one line; each point on a given panel is for a single map measured at the corresponding box size $ϵ$. Our goal was to estimate $D$ assuming that the object was fractal, rather than assess whether the object was actually fractal. Using the box‐counting method with a random origin, the resulting estimates of 𝐷 are low for small 𝜖 (as predicted based on issue (ii); see Box 2) and large 𝜖 (as predicted based on issue (i); see Box 2), but accurate for intermediate $ϵ\approx 32-128$ (points are close to 1:1 line). We ran a similar analysis using maps generated from a Gaussian random field algorithm and again found that the results of the box‐counting algorithm were most accurate for intermediate $ϵ\approx 64$, although the errors were larger than for the midpoint‐displacement maps (Supporting Information S4).