Figure 1.

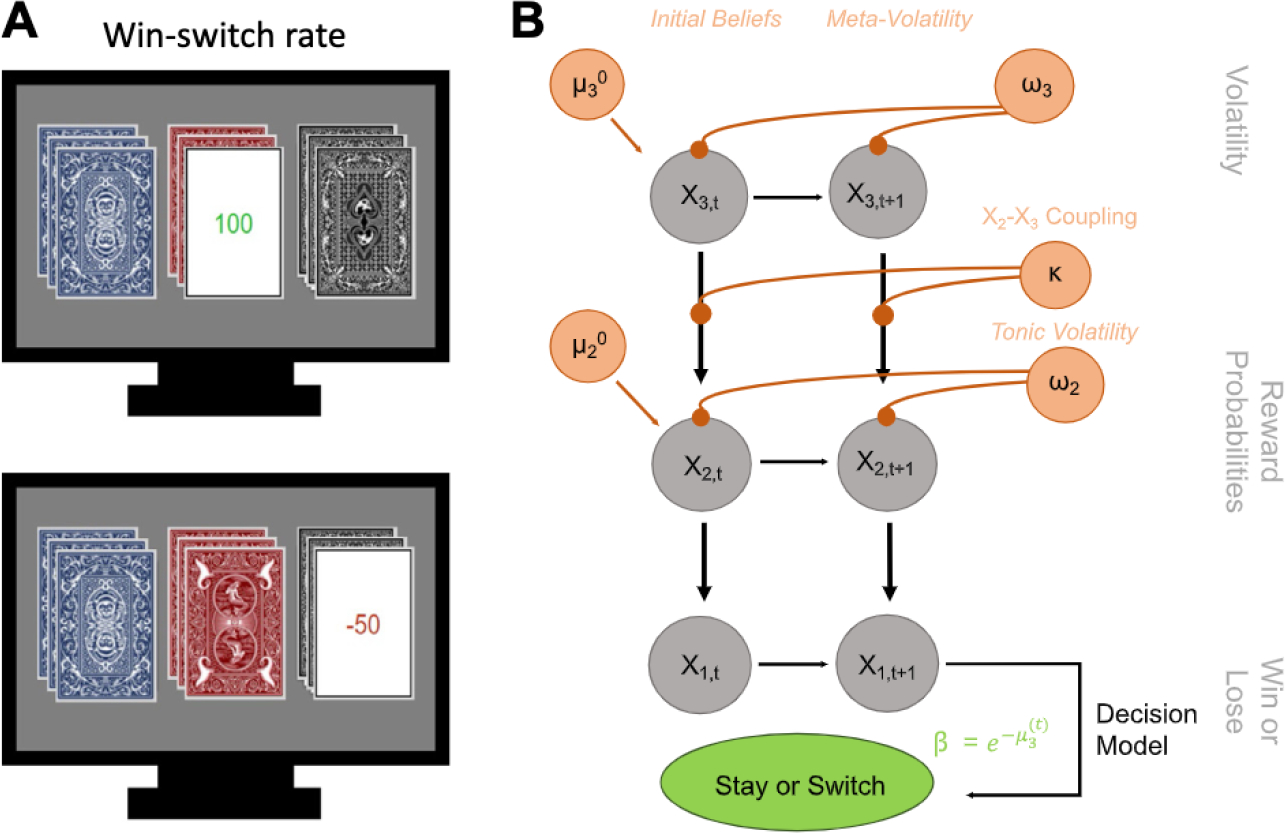
(A) Task image of 3-option probabilistic reversal learning. Participants are simultaneously shown 3 decks of cards and are asked to select a card from any of the decks using keys on the computer keyboard. Once a deck is selected, the card is flipped to reveal whether that card won (+100) or lost (−50) them points. At the start of the task, participants are instructed to earn as many points as possible. They are also told that, while all of the decks include both winning and losing cards, one of the decks is best and will win them the most points. Finally, they are told that the best deck may change during the task and, if they believe it has changed, they should find the new best deck. Reward contingencies begin at 90%/50%/10% to support development of strong beliefs about the task environment and then, unbeknownst to the participant, change to 80%/40%/20%. (B) Schematic of the 3-level Hierarchical Gaussian Filter model using a Softmax decision model. Level 1 (x1) represents trial-by-trial win or loss feedback. Level 2 (x2) is the stimulus-outcome association (reward probabilities of the decks). Level 3 (x3) is the perception of the overall reward contingency context (volatility). Initial beliefs about task volatility are captured by μ⁰₃, which reflects a participant’s expectation about instability and change in the task before new evidence is encountered. Readiness to learn about changes in the volatility of the task are captured by the meta-volatility rate (ω₃), which indexes how stable the changes in underlying contingencies of the decks might be. Higher values imply a more rapid adjustment of their volatility belief. Sensitivity to that volatility (i.e., the impact of phasic volatility on stimulus-outcome associations) is captured by κ, whereas ω₂ reflects the tonic volatility of stimulus-outcome associations, with lower values indicating slower adjustment of beliefs about the value of each deck choice.